1.2 直角三角形(1)同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
1.2直角三角形（一）同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
1.定理 在直角三角形中，如果一个锐角等于30°，那么它所对的直角 边等于斜边的一半.
2.直角三角形的性质：
直角三角形的两个锐角互余.
直角三角形两条直角边的平方和等于斜边的平方.
3.了解互逆命题，逆命题。
基础知识和能力拓展训练
一 、选择题
将一副直角三角尺如图放置，若∠AOD=20°，则∠BOC的大小为（ ）
A．140° B．160° C．170° D．150°
如图，AB∥CD，DB⊥BC，∠1=40°，则∠2的度数是( )
A．40° B．50° C．60° D．140°
如图，△ABC中，∠C=90°，AC=3，∠B=30°，点P是BC边上的动点，则AP长不可能是( )
A．5 B．4 C．7 D．6
如图，AB∥CD，AE交CD于C，∠A=34°，∠DEC=90°，则∠D的度数为（ ）
A．17° B．34° C．56° D．124°
已知等边三角形的面积为4，则它的边长为（ ）
A．6 B.5 C.4 D．3
如图，△ABC中，∠C=90°，∠A=30°，AB=12，则BC=（　　）
A．6 B．6 C．6 D．12
如图，等边△ABC的高AH等于，那么该三角形的面积为（ ）
A． B．2 C．2 D．4
如图折叠直角三角形纸片的直角，使点C落在斜边AB上的点E处，已知CD=1，∠B=30°，则BD的长是（　　）
A．1 B．2 C． D．2
如图，直线a∥b，AC⊥AB，AC交直线b于点C，∠1=60°，则∠2的度数是（　　）
A．50° B．45° C．35° D．30°
在△ABC中，∠A：∠B：∠C=1：2：3，最短边BC=4cm，则最长边AB的长是（　　）
A．5cm B．6cm C．cm D．8cm
下列命题是真命题的是（ ）
A．如果两个角不相等，那么这两个角不是对顶角
B．如果a2=b2，那么a=b
C．两互补的角一定是邻补角
D．如果两角是同位角，那么这两角一定相等
二 、填空题
若直角三角形的一个锐角为50°，则另一个锐角的度数是　　　　　　度．
如图，小雅家（图中点O处）门前有一条东西走向的公路，经测得有一水塔（图中
点A处）在她家北偏东60°500m处，那么水塔所在的位置到公路的距离AB是　 　．
如图，直线a∥b，EF⊥CD于点F，∠2=65°，则∠1的度数是　　　　　　．
如图，∠AOP=∠BOP=15°，PC∥OA，PD⊥OA，若PC=4，则PD的长为_____________
如图，四边形ABCD中，AB=AD，AD∥BC，∠ABC=60°，∠BCD=30°，BC=6，那么△ACD的面积是　　　　　　．
三 、解答题
已知：如图，中，于D.
求证：。
如图，在△ABC中，∠ACB=90°，∠A=30°，BD平分∠ABC．求证：AD=2CD．
如图，一艘轮船从点A向正北方向航行，每小时航行15海里，小岛P在轮船的北偏西15°，3小时后轮船航行到点B，小岛P此时在轮船的北偏西30°方向，在小岛P的周围20海里范围内有暗礁，如果轮船不改变方向继续向前航行，是否会有触礁危险？请说明理由。
(
A
B
P
C
北
)
`
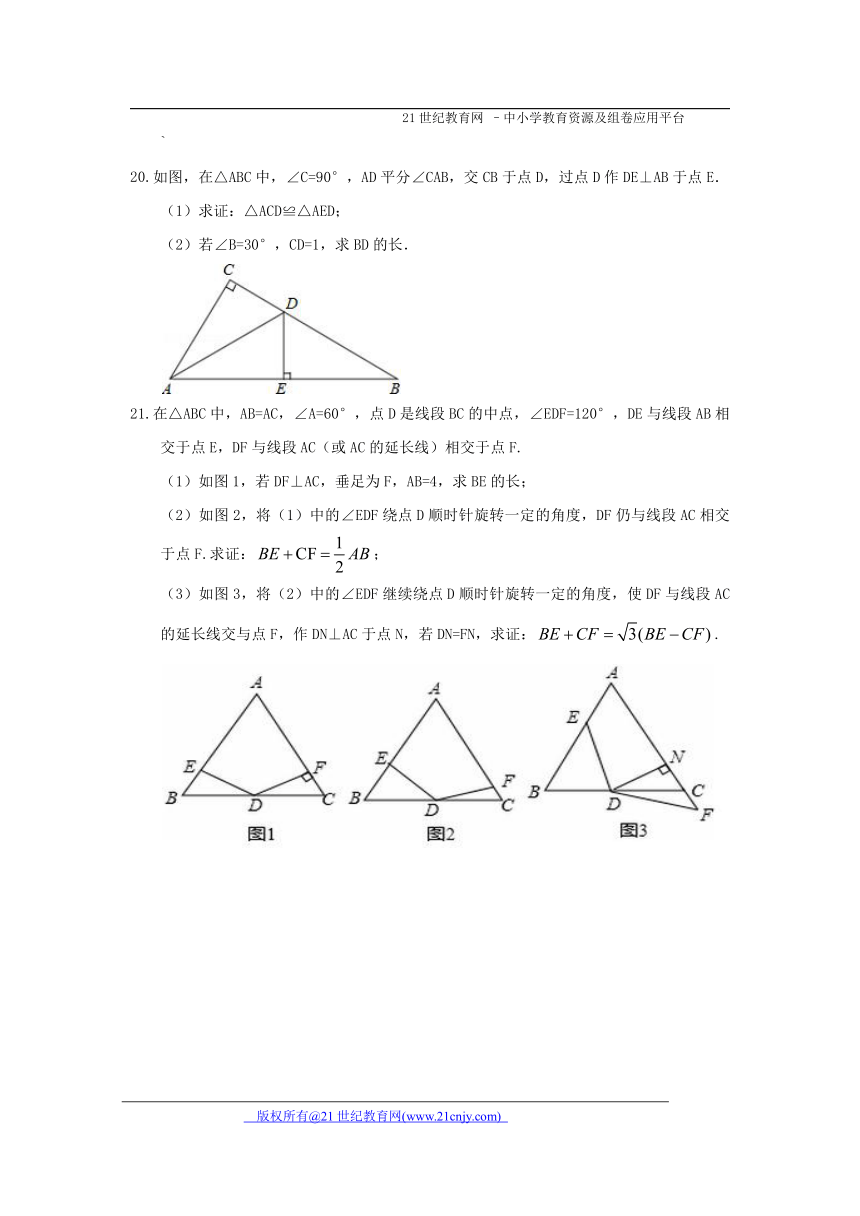
如图，在△ABC中，∠C=90°，AD平分∠CAB，交CB于点D，过点D作DE⊥AB于点E．
（1）求证：△ACD≌△AED；
（2）若∠B=30°，CD=1，求BD的长．
在△ABC中，AB=AC，∠A=60°，点D是线段BC的中点，∠EDF=120°，DE与线段AB相交于点E，DF与线段AC（或AC的延长线）相交于点F.
（1）如图1，若DF⊥AC，垂足为F，AB=4，求BE的长；
（2）如图2，将（1）中的∠EDF绕点D顺时针旋转一定的角度，DF仍与线段AC相交于点F.求证：；
（3）如图3，将（2）中的∠EDF继续绕点D顺时针旋转一定的角度，使DF与线段AC的延长线交与点F，作DN⊥AC于点N，若DN=FN，求证：.
答案解析
一 、选择题
【分析】利用直角三角形的性质求解
解：∵∠AOD=20°，∴∠COA=90°﹣20°=70°，∴∠BOC=90°+70°=160°．
故选B
【分析】先根据平行线的性质求出∠3的度数，再根据直角三角形的性质即可得出∠2的度数．
解：∵AB∥CD，∠1=40°，
∴∠3=∠1=40°，
∵DB⊥BC，
∴∠2=90°﹣∠3=90°﹣40°=50°．
故选B．
【分析】利用垂线段最短分析AP最小不能小于3；利用含30度角的直角三角形的性质得出AB=6，可知AP最大不能大于6．此题可解．
解：根据垂线段最短，可知AP的长不可小于3；
∵△ABC中，∠C=90°，AC=3，∠B=30°，
∴AB=6，
∴AP的长不能大于6．
故选C．
【分析】由平行线的性质得出∠DCE=∠A，再由直角三角形的性质求解
解：∵AB∥CD，
∴∠DCE=∠A=34°，
∵∠DEC=90°，
∴∠D=90°﹣∠DCE=90°﹣34°=56°．
故选C．
【分析】作出等边三角形边上高，利用60°的正弦值可表示出高的值，利用三角形的面积公式求解即可．
解：如图，作AD⊥BC于点D．
设AB=BC=AC=x，
则AD=AB×sin∠B= x，
故边长为x的等边三角形的面积为 ×x× x=4 ，
解得：x=4，
故选：C．
【分析】根据30°所对的直角边等于斜边的一半求解．
解：∵∠C=90°，∠A=30°，AB=12，
∴BC=12sin30°=12×=6，
故答选A．
【分析】利用等边三角形的性质以及解直角三角形的知识求出BC的长，即可求出△ABC的面积．
解：∵AB=AC=BC， ∴BH=CH= CB= AB，∠BAH=30°，
∵AH= ，
∴cos30°= ，
∴AB= =2cm，
∴BC=2cm，
∴△ABC的面积为： CB AH= ×2× = （cm2）．
故选A．
【分析】由轴对称的性质可以得出DE=DC，∠AED=∠C=90°，就可以得出∠BED=90°，根据直角三角形的性质就可以求出BD=2DE，然后解答即可．
解：∵△ADE与△ADC关于AD对称，
∴△ADE≌△ADC，
∴DE=DC，∠AED=∠C=90°，
∴∠BED=90°．
∵∠B=30°，
∴BD=2DE．
∵DC=1，
∴BD=2．
故选：B
【分析】根据平行线的性质，可得∠3与∠1的关系，根据两直线垂直，可得所成的角是90°，根据角的和差，可得答案．
解：如图，
∵直线a∥b，
∴∠3=∠1=60°．
∵AC⊥AB，
∴∠3+∠2=90°，
∴∠2=90°﹣∠3=90°﹣60°=30°，
故选：D．
【分析】利用三角形的内角和和角的比求出三角的度数，再由最小边BC=4cm，即可求出最长边AB的长．
解答： 解：设∠A=x，
则∠B=2x，∠C=3x，
由三角形内角和定理得∠A+∠B+∠C=x+2x+3x=180°，
解得x=30°，
即∠A=30°，∠C=3×30°=90°，
即△ABC为直角三角形，
∵∠C=90°，∠A=30°，
∴AB=2BC=2×4=8cm，
故选D．
【分析】根据对顶角相等对A进行判断；根据a=-b时，有a2=b2，可对B进行判断；根据邻补角的定义对C进行判断；根据平行线的性质对D进行判断．
解：A、如果两个角不相等，那么这两个角一定不是对顶角，所以A选项为真命题；
B、如果a2=b2，那么a=b或a=-b，所以B选项为假命题；
C、有个角有一条公共边且互补的角一定是邻补角，所以C选项为假命题；
D、当两直线平行，且两角是同位角，那么这两角一定相等，所以D选项为假命题．
故选A．
二 、填空题
【分析】根据直角三角形两锐角互余解答．
解：∵一个锐角为50°，
∴另一个锐角的度数=90°﹣50°=40°．
故答案为：40°．
【分析】求出∠AOB，根据含30度角的直角三角形性质求出即可．
解：∠AOB=90°﹣60°=30°，
∵∠ABO=90°，OA=500m，
∴AB=OA=250m，
故答案为：250m．
【分析】先根据直线a∥b，∠2=65°得出∠FDE的度数，再由EF⊥CD于点F可知∠DFE=90°，故可得出∠1的度数．
解：∵直线a∥b，∠2=65°，
∴∠FDE=∠2=65°，
∵EF⊥CD于点F，
∴∠DFE=90°，
∴∠1=90°﹣∠FDE=90°﹣65°=25°．
故答案为：25°．
【分析】过P作PE垂直与OB，由∠AOP=∠BOP，PD垂直于OA，利用角平分线定理得到PE=PD，由PC与OA平行，根据两直线平行得到一对内错角相等，又OP为角平分线得到一对角相等，等量代换可得∠COP=∠CPO，又∠ECP为三角形COP的外角，利用三角形外角的性质求出∠ECP=30°，在直角三角形ECP中，由30°角所对的直角边等于斜边的一半，由斜边PC的长求出PE的长，即为PD的长．
解答： 解：过P作PE⊥OB，交OB与点E，
∵∠AOP=∠BOP，PD⊥OA，PE⊥OB，
∴PD=PE，
∵PC∥OA，
∴∠CPO=∠POD，
又∠AOP=∠BOP=15°，
∴∠CPO=∠BOP=15°，
又∠ECP为△OCP的外角，
∴∠ECP=∠COP+∠CPO=30°，
在直角三角形CEP中，∠ECP=30°，PC=4，
∴PE=PC=2，
则PD=PE=2．
故答案为：2．
【分析】如图，过点A作AE⊥BC于E，过点D作DF⊥BC于F．构建矩形AEFD和直角三角形，通过含30度角的直角三角形的性质求得AE的长度，然后由三角形的面积公式进行解答即可．
解：如图，过点A作AE⊥BC于E，过点D作DF⊥BC于F．设AB=AD=x．
又∵AD∥BC，
∴四边形AEFD是矩形形，
∴AD=EF=x．
在Rt△ABE中，∠ABC=60°，则∠BAE=30°，
∴BE=AB=x，
∴DF=AE==x，
在Rt△CDF中，∠FCD=30°，则CF=DF cot30°=x．
又∵BC=6，
∴BE+EF+CF=6，即x+x+x=6，
解得 x=2
∴△ACD的面积是： AD DF=x×x=×22=，
故答案为：．
三 、解答题
证明：过点A作于E，
,
所以（等腰三角形的三线合一性质）
因为
又，所以
所以（直角三角形两锐角互余）
所以（同角的余角相等）
即
【分析】过D作DE⊥AB于E，根据角平分线性质得出CD=DE，根据含30度角的直角三角形性质得出AD=2DE，代入求出即可．
证明：
过D作DE⊥AB于E，
∵∠ACB=90°，BD平分∠ABC，
∴CD=DE，∠DEA=90°，
∵∠A=30°，
∴AD=2DE，
∴AD=2CD
解：连接AP，且做PD垂直于AB交AB延长线于D点
∵∠PBC=30°∴∠PBA=150°
又∵∠A=15°
∴∠APB=15°（180-150-15）
∴PB=PA=45×3=45海里
∴PD=22.5海里(30度角所对的边等于斜边一半)
22.5大于20，所以不会触礁。
【分析】（1）利用角平分线的性质求出CD=ED，再利用HL定理
(2)求出∠DEB=90°再利用含30度角的直角三角形的性质求出
（1）证明：∵AD平分∠CAB，DE⊥AB，∠C=90°，
∴CD=ED，∠DEA=∠C=90°，
∵在Rt△ACD和Rt△AED中
∴Rt△ACD≌Rt△AED（HL）；
（2）解：∵DC=DE=1，DE⊥AB，
∴∠DEB=90°，
∵∠B=30°，
∴BD=2DE=2．
【分析】根据四边形的内角和定理得出DE⊥AB，从而得到BE的长度；取AB的中点G，连接DG，得出DG为△ABC的中位线，则DG=DC，∠BGD=∠C=60°，根据四边形对角互补得出∠GED=∠DFC，从而得到△DEG和△DFC全等，得到EG=CF，得出答案；取AB的中点G，连接DG，同⑵，易证△DEG≌△DFC得出EG=CF，设CN=x，根据Rt△DCN得出CD=2x，DN=x，根据题意得出EG、BE与x的关系，从而进行说明．
解：⑴由四边形AEDF的内角和为360°，可知DE⊥AB，故BE＝２
⑵取AB的中点G，连接DG
易证：DG为△ABC的中位线，故DG=DC，∠BGD＝∠C＝60°
又四边形AEDF的对角互补，故∠GED＝∠DFC
∴△DEG≌△DFC
故EG=CF
∴BE+CF=BE+EG=BG=AB
⑶取AB的中点G，连接DG
同⑵，易证△DEG≌△DFC
故EG=CF
故BE-CF=BE-EG=BG=AB
设CN＝x
在Rt△DCN中，CD=2x，DN=x
在RT△DFN中，NF=DN=x，故EG=CF=（-1）x
BE=BG+EG=DC+CF=2x+（-1）x =（+1）x
故BE+CF=（+1）x+（-1）x＝２x，
（BE-CF）=[(+1) x-（-1）x]= ２x.
故.
版权所有@21世纪教育网(www.21cnjy.com)