1.3 直角三角形全等的判定同步练习
文档属性
| 名称 | 1.3 直角三角形全等的判定同步练习 |

|
|
| 格式 | docx | ||
| 文件大小 | 242.4KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-28 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
1.3直角三角形全等的判定同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
直角三角形全等的判定除了可以运用以前学过的 SAS、 ASA 、 AAS 、SSS 方法外,还有自己特殊的方法,即 斜边、直角边定理,其内容是:有斜边和一条直角边对应相等的两个直角三角 形全等 ,也可简写成 HL .
基础知识和能力拓展训练
一、选择题
如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC △DAE的是( )
A. AC=AE B. BC=DE C. ∠B=∠D D. ∠C=∠E
下列条件中,能判定两个直角三角形全等的是( )
A.一锐角对应相等 B.两锐角对应相等
C.一条边对应相等 D.两条直角边对应相等
要判定两个直角三角形全等,下列说法正确的有( )
①有两条直角边对应相等;
②有两个锐角对应相等;
③有斜边和一条直角边对应相等;
④有一条直角边和一个锐角相等;
⑤有斜边和一个锐角对应相等;
⑥有两条边相等.
A.6个 B.5个 C.4个 D.3个
下列说法不正确的是( )
A.有两个角和一条边对应相等的两个三角形全等
B.有一条边和一个锐角对应相等的两个直角三角形全等
C.有两边和其中一边的对角对应相等的两个三角形全等
D.有两条直角边对应相等的两个直角三角形全等
下列说法中,正确的是( )
A.直角三角形中,已知两边长为3和4,则第三边长为5
B.三角形是直角三角形,三角形的三边为a,b,c则满足a2﹣b2=c2
C.以三个连续自然数为三边长不可能构成直角三角形
D.△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形
能使两个直角三角形全等的条件是( )
A.斜边相等 B.两直角边对应相等
C.两锐角对应相等 D.一锐角对应相等
已知下列语句:
①有两个锐角相等的直角三角形全等;
②一条斜边对应相等的两个直角三角形全等;
③三个角对应相等的两个三角形全等;
④两个直角三角形全等.
其中正确语句的个数为( )
A.0 B.1 C.2 D.3
如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.SSS B.ASA C.SSA D.HL
如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于O,AO的延长线交BC于F,则图中全等的直角三角形有( )
A.3对 B.4对 C.5对 D.6对
二、填空题
如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“________”.
如图∠C=∠D=900 , 要使△ABC≌△BAD需要添加的一个条件是________.
①有两边和一角对应相等的两个三角形全等;②斜边和一条直角边对应相等的两个直角三角形全等;③有三角对应相等的两个直角三角形全等;④有两角和其中一角的对边对应相等的两个三角形全等;
上述判断正确的是________.
如图所示,∠C=∠D=90°,可使用“HL”判定Rt△ABC与Rt△ABD全等,则应添加一个条件是________
如图,已知四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,那么Rt△ABC≌Rt△ADC,根据是________.
如图,MN∥PQ,AB⊥PQ,点A.D、B、C分别在直线MN与PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB= ________
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为9,则BE= ________
三、解答题
如图,∠ABD=∠ACD=90°,∠1=∠2.求证:AD平分∠BDC。
如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
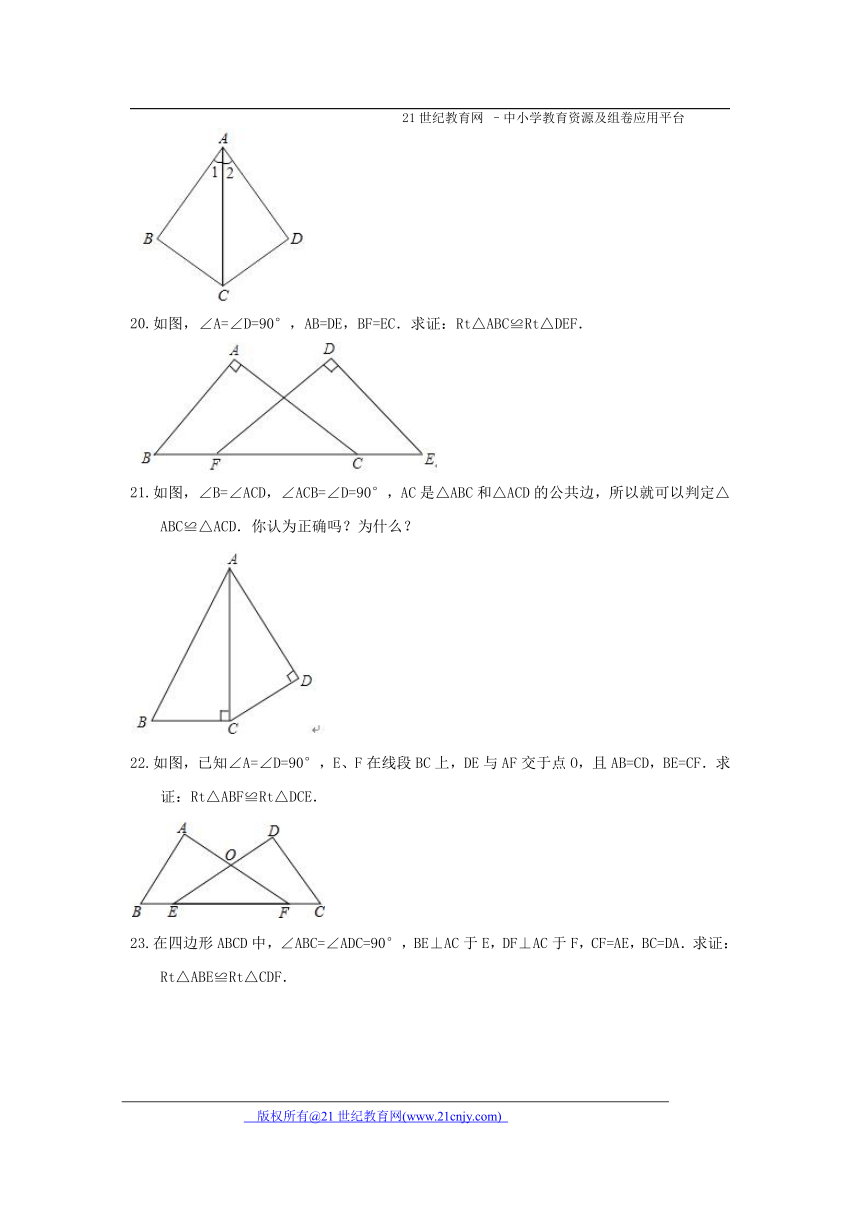
如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
如图,∠B=∠ACD,∠ACB=∠D=90°,AC是△ABC和△ACD的公共边,所以就可以判定△ABC≌△ACD.你认为正确吗?为什么?
如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.
在四边形ABCD中,∠ABC=∠ADC=90°,BE⊥AC于E,DF⊥AC于F,CF=AE,BC=DA.求证:Rt△ABE≌Rt△CDF.
如图,点C在BE上,AB⊥BE,DE⊥BE,且AB=BE,BC=DE,AC交BD于F.
(1)求证:△ABC≌△BED;
(2)求∠BFC的度数.
答案解析
一 、选择题
【考点】直角三角形全等的判定
【分析】从得到的∠BAD=∠CAE,则∠BAC=∠DAE,从而在△BAC和△DAE中,有∠BAC=∠DAE,和AB=AD,所以只要根据“SAS”“ASA”“AAS”的判定定理判断即可.
解:已知∠BAD=∠CAE,则∠BAC=∠DAE,又AB=AD,
当根据“SAS”时,可添加“AC=AE”,故A能判定,故B不能判定;
当根据“ASA”时,可添加“∠B=∠D”,故C能判定;
当根据“AAS”时,可添加“∠C=∠E”,故D能判定;
故选B.
【考点】直角三角形全等的判定
【分析】判定两个直角三角形全等的方法有:SAS、SSS、AAS、ASA.HL五种,然后结合题目所给的条件进行判断即可.
解:两直角三角形隐含一个条件是两直角相等,要判定两直角三角形全等,起码还要两个条件,故可排除A.C;
而B构成了AAA,不能判定全等;
D构成了SAS,可以判定两个直角三角形全等.
故答案为:D.
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定方法及“HL”定理,判断即可.
解:①有两条直角边对应相等,可以利用SAS证明全等,正确; ②有两个锐角对应相等,不能利用AAA证明全等,错误;
③有斜边和一条直角边对应相等,可以利用HL证明全等,正确;
④有一条直角边和一个锐角相等,可以利用AAS证明全等,正确;
⑤有斜边和一个锐角对应相等,可以利用AAS证明全等,正确;
⑥有两条边相等,可以利用HL或SAS证明全等,正确;
故选B
【考点】直角三角形全等的判定
【分析】根据三角形全等的判定定理进行分析即可.
解:A.有两个角和一条边对应相等的两个三角形全等,说法正确;
B.有一条边和一个锐角对应相等的两个直角三角形全等,说法正确;
C、有两边和其中一边的对角对应相等的两个三角形全等,说法错误;
D、有两条直角边对应相等的两个直角三角形全等,说法正确;
故选:C
【考点】直角三角形全等的判定
【分析】根据直角三角形的判定进行分析,从而得到答案.
解:A.应为“直角三角形中,已知两直角边的边长为3和4,则斜边的边长为5”,故错误;
B、应为“三角形是直角三角形,三角形的直角边分别为a,b,斜边为c则满足a2﹣b2=c2”,故错误;
C、比如:边长分别为3,4,5,有32+42=25=52 , 能构成直角三角形,故错误;
D、根据三角形内角和定理可求出三个角分别为15°,75°,90°,因而是直角三角形,故正确.
故选D.
【考点】直角三角形全等的判定
【分析】要判断能使两个直角三角形全等的条件首先要看现在有的条件:一对直角对应相等,还需要两个条件,而AAA是不能判定三角形全等的,所以正确的答案只有选项B了.
解:A选项,无法证明两条直角边对应相等,因此A错误.
C、D选项,在全等三角形的判定过程中,必须有边的参与,因此C、D选项错误.
B选项的根据是全等三角形判定中的SAS判定.
故选:B.
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定定理HL、SAS、AAS、ASA分别进行分析即可.
解:①有两个锐角相等的直角三角形全等,说法错误;②一条斜边对应相等的两个直角三角形全等,说法错误;③三个角对应相等的两个三角形全等,说法错误; ④两个直角三角形全等,说法错误.故选:A.
【考点】直角三角形全等的判定
【分析】先证AO为角平分线,再根据直角三角形全等的判别方法HL可证△AOD≌△AOP.
解:∵OD=OP,OD⊥AB且OP⊥AC,
∴AO为角平分线,
∴△ADO和△OPO是直角三角形,
又∵OD=OP且AO=AO
∴△AOD≌△AOP.
故选D.
【考点】直角三角形全等的判定
【分析】△ADO≌△AEO,△DOC≌△EOB,△COF≌△BOF,△ACF≌△ABF,△ADB≌△AEC,△BCE≌△CBD.
利用全等三角形的判定可证明,做题时,要结合已知条件与三角形全等的判定方法逐个验证.
解:∵BD⊥AC,CE⊥AB,∴∠ADB=∠AEC=90°,
∵AC=AB,
∵∠CAE=∠BAD,
∴△AEC≌△ADB;
∴CE=BD,
∵AC=AB,
∴∠CBE=∠BCD,
∵∠BEC=∠CDB=90°,
∴△BCE≌△CBD;
∴BE=CD,
∴AD=AE,
∵AO=AO,
∴△AOD≌△AOE;
∵∠DOC=∠EOB,
∴△COD≌△BOE;
∴OB=OC,
∵AB=AC,
∴CF=BF,AF⊥BC,
∴△ACF≌△ABF,△COF≌△BOF.
共6对,故选D.
二 、填空题
【考点】直角三角形全等的判定
【分析】首先根据三角形的高可得两个高所在的三角形是直角三角形,再根据由已知一组直角边和一组斜边相等,利用直角三角形的判断方法,可得两个直角三角形全等.
解: 因为BE,CD是△ABC的高,所以∠CDB=∠BEC=90°, △CDB和△BEC是直角三角形;且BD=EC,BC=CB所以△BCD≌△CBE;
【考点】直角三角形全等的判定
解:∵∠C=∠D=90°,AB=BA,
∴可以添加AC=BD或BC=AD利用HL判定△ABC≌△BAD;
添加∠ABC=∠BAD或∠CAB=∠DBA利用AAS判定△ABC≌△BAD.
故应填:AC=BD或BC=AD或∠ABC=∠BAD或∠CAB=∠DBA,
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定定理,针对每一个选项进行分析,可得答案.
解:①有两边和一角对应相等的两个三角形不一定全等,错误; ②斜边和一条直角边对应相等的两个直角三角形全等,正确;
③有三角对应相等的两个直角三角形不一定全等,错误;
④有两角和其中一角的对边对应相等的两个三角形全等,正确;
故答案为:②④
【考点】直角三角形全等的判定
【分析】此题是一道开放型的题目,答案不唯一,还可以是BC=BD.
解:条件是AC=AD,∵∠C=∠D=90°,
在Rt△ABC和Rt△ABD中
∴Rt△ABC≌Rt△ABD(HL),
故答案为:AC=AD.
【考点】直角三角形全等的判定
【分析】因为∠ABC=∠ADC=90°,所以△ABC和△ADC为直角三角形,又因为CB=CD,CA=CA,故可根据HL判定Rt△ABC≌Rt△ADC.
解:∵∠ABC=∠ADC=90°,CB=CD,CA=CA
∴Rt△ABC≌Rt△ADC(HL).
故填HL.
【考点】直角三角形全等的判定
【分析】可判定△ADE≌△BCE,从而得出AE=BC,则AB=AD+BC.
解:∵MN∥PQ, AB⊥PQ,
∴AB⊥MN,
∴∠DAE=∠EBC=90°,
在Rt△ADE和Rt△BCE中,
∴△ADE≌△BEC(HL),
∴AE=BC,
∵AD+BC=7,
∴AB=AE+BE=AD+BC=7.
故答案为7.
【考点】直角三角形全等的判定,正方形的判定
【分析】作BF⊥CD交CD的延长线于点F,据条件可证得∠ABE=∠CBF,且由已知∠AEB=∠CFB=90°,AB=BC,所以△ABE≌△CBF,可得BE=BF;四边形ABCD的面积等于新正方形FBED的面积(需证明是正方形),即可得BE=3.
解:过B作BF垂直DC的延长线交于点F,∵∠ABC=∠CDA=90°,BF⊥CD,
∴∠ABE+∠EBC=∠CBF+∠EBC,∴∠ABE=∠CBF;
又∵BE⊥AD,BF⊥DF,且AB=BC,
∴△ABE≌△CBF,即BE=BF;
∵BE⊥AD,∠CDA=90°,BE=BF,
∴四边形BEDF为正方形;
由以上得四边形ABCD的面积等于正方形BEDF的面积,即等于9,
∴BE2=9,即BE=3.
三 、解答题
【考点】直角三角形全等的判定
【分析】由∠1=∠2,根据等角对等边,可得BD=CD;在Rt△ABD和Rt△ACD中,AD是公共边,根据HL定理可判定Rt△ABD≌Rt△ACD,进而得到∠ADB=∠ADC即AD平分∠BDC.
解:∵∠1=∠2∴BD=CD
∵AD=AD
∴Rt△ABD≌Rt△ACD
∴∠ADB=∠ADC
即AD平分∠BDC
【考点】直角三角形的性质,直角三角形全等的判定
【分析】先利用HL判定△CAE≌△EBD,从而得出全等三角形的对应角相等,再利用角与角之间的关系,可以得到线段CE与DE的大小与位置关系为相等且垂直.
解:CE=DE,CE⊥DE,理由如下:
∵AC⊥AB,DB⊥AB,
AC=BE,AE=BD,
∴△CAE≌△EBD.
∴∠CEA=∠D.
∵∠D+∠DEB=90°,
∴∠CEA+∠DEB=90°.
即线段CE与DE的大小与位置关系为相等且垂直.
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定定理AAS进行证明.
解:△ABC≌△ADC.理由如下: ∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS)
【考点】直角三角形全等的判定
【分析】先由BF=EC得到BC=EF,再根据“HL”判定Rt△ABC≌Rt△DEF.
证明:∵BF=EC,
∴BF+FC=FC+EC,即BC=EF,
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).
【考点】直角三角形全等的判定
【分析】根据直角三角形全等的判定方法:斜边和一条直角边对应相等的两个直角三角形全等进行分析即可.
解:不正确,
因为AC不是△ABC和△ACD的对应边,故不能判定△ABC≌△ACD.
【考点】直角三角形全等的判定
【分析】根据已知条件BE=CF,由线段的和差,得到BF=CE,根据HL得到Rt△ABF≌Rt△DCE.
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,
∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,
BC=CE,AB=CD,
∴Rt△ABF≌Rt△DCE(HL)
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定定理HL证得Rt△ADC≌Rt△CBA,在该全等三角形的对应边相等:DC=BA,然后再由HL来证得Rt△ABE≌Rt△CDF.
解:如图,
在Rt△ADC与Rt△CBA中,
∴Rt△ADC≌Rt△CBA(HL),
∴DC=BA.
又∵BE⊥AC于E,DF⊥AC于F,
∴∠AEB=∠CFD=90°,
在Rt△ABE与Rt△CDF中,
∴Rt△ABE≌Rt△CDF(HL).
【考点】直角三角形全等的判定
【分析】(1)在两个直角三角形中,已知的条件有:AB=BE、BC=DE、∠ABC=∠E=90°,即可由SAS判定两个三角形全等.
(2)根据(1)题证得的全等三角形,可得到∠DBE=∠A,由于∠A.∠BCF互余,所以∠FBC、∠BCF互余,即∠BFC是直角.
(1)证明:∵AB⊥BE,DE⊥BE,
∴∠ABC=∠BED=90°,
在△ABC和△BED中,
∴△ABC≌△BED(SAS);
(2)解:∵△ABC≌△BED,
∴∠DBE=∠CAB,
∵∠ABC=90°,
∴∠CAB+∠ACB=90°.
∴∠DBE+∠ACB=90°.
∴在△BFC中,∠BFC=90°.
版权所有@21世纪教育网(www.21cnjy.com)
1.3直角三角形全等的判定同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
直角三角形全等的判定除了可以运用以前学过的 SAS、 ASA 、 AAS 、SSS 方法外,还有自己特殊的方法,即 斜边、直角边定理,其内容是:有斜边和一条直角边对应相等的两个直角三角 形全等 ,也可简写成 HL .
基础知识和能力拓展训练
一、选择题
如图,已知AB=AD,∠BAD=∠CAE,则增加以下哪个条件仍不能判断△BAC △DAE的是( )
A. AC=AE B. BC=DE C. ∠B=∠D D. ∠C=∠E
下列条件中,能判定两个直角三角形全等的是( )
A.一锐角对应相等 B.两锐角对应相等
C.一条边对应相等 D.两条直角边对应相等
要判定两个直角三角形全等,下列说法正确的有( )
①有两条直角边对应相等;
②有两个锐角对应相等;
③有斜边和一条直角边对应相等;
④有一条直角边和一个锐角相等;
⑤有斜边和一个锐角对应相等;
⑥有两条边相等.
A.6个 B.5个 C.4个 D.3个
下列说法不正确的是( )
A.有两个角和一条边对应相等的两个三角形全等
B.有一条边和一个锐角对应相等的两个直角三角形全等
C.有两边和其中一边的对角对应相等的两个三角形全等
D.有两条直角边对应相等的两个直角三角形全等
下列说法中,正确的是( )
A.直角三角形中,已知两边长为3和4,则第三边长为5
B.三角形是直角三角形,三角形的三边为a,b,c则满足a2﹣b2=c2
C.以三个连续自然数为三边长不可能构成直角三角形
D.△ABC中,若∠A:∠B:∠C=1:5:6,则△ABC是直角三角形
能使两个直角三角形全等的条件是( )
A.斜边相等 B.两直角边对应相等
C.两锐角对应相等 D.一锐角对应相等
已知下列语句:
①有两个锐角相等的直角三角形全等;
②一条斜边对应相等的两个直角三角形全等;
③三个角对应相等的两个三角形全等;
④两个直角三角形全等.
其中正确语句的个数为( )
A.0 B.1 C.2 D.3
如图,OD⊥AB于D,OP⊥AC于P,且OD=OP,则△AOD与△AOP全等的理由是( )
A.SSS B.ASA C.SSA D.HL
如图,△ABC中,AB=AC,BD⊥AC于D,CE⊥AB于E,BD和CE交于O,AO的延长线交BC于F,则图中全等的直角三角形有( )
A.3对 B.4对 C.5对 D.6对
二、填空题
如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“________”.
如图∠C=∠D=900 , 要使△ABC≌△BAD需要添加的一个条件是________.
①有两边和一角对应相等的两个三角形全等;②斜边和一条直角边对应相等的两个直角三角形全等;③有三角对应相等的两个直角三角形全等;④有两角和其中一角的对边对应相等的两个三角形全等;
上述判断正确的是________.
如图所示,∠C=∠D=90°,可使用“HL”判定Rt△ABC与Rt△ABD全等,则应添加一个条件是________
如图,已知四边形ABCD中,CB=CD,∠ABC=∠ADC=90°,那么Rt△ABC≌Rt△ADC,根据是________.
如图,MN∥PQ,AB⊥PQ,点A.D、B、C分别在直线MN与PQ上,点E在AB上,AD+BC=7,AD=EB,DE=EC,则AB= ________
如图,在四边形ABCD中,AB=BC,∠ABC=∠CDA=90°,BE⊥AD于点E,且四边形ABCD的面积为9,则BE= ________
三、解答题
如图,∠ABD=∠ACD=90°,∠1=∠2.求证:AD平分∠BDC。
如图,已知AC⊥AB,DB⊥AB,AC=BE,AE=BD,试猜想线段CE与DE的大小与位置关系,并证明你的结论.
已知:AB⊥BC,AD⊥DC,∠1=∠2,问:△ABC≌△ADC吗?说明理由.
如图,∠A=∠D=90°,AB=DE,BF=EC.求证:Rt△ABC≌Rt△DEF.
如图,∠B=∠ACD,∠ACB=∠D=90°,AC是△ABC和△ACD的公共边,所以就可以判定△ABC≌△ACD.你认为正确吗?为什么?
如图,已知∠A=∠D=90°,E、F在线段BC上,DE与AF交于点O,且AB=CD,BE=CF.求证:Rt△ABF≌Rt△DCE.
在四边形ABCD中,∠ABC=∠ADC=90°,BE⊥AC于E,DF⊥AC于F,CF=AE,BC=DA.求证:Rt△ABE≌Rt△CDF.
如图,点C在BE上,AB⊥BE,DE⊥BE,且AB=BE,BC=DE,AC交BD于F.
(1)求证:△ABC≌△BED;
(2)求∠BFC的度数.
答案解析
一 、选择题
【考点】直角三角形全等的判定
【分析】从得到的∠BAD=∠CAE,则∠BAC=∠DAE,从而在△BAC和△DAE中,有∠BAC=∠DAE,和AB=AD,所以只要根据“SAS”“ASA”“AAS”的判定定理判断即可.
解:已知∠BAD=∠CAE,则∠BAC=∠DAE,又AB=AD,
当根据“SAS”时,可添加“AC=AE”,故A能判定,故B不能判定;
当根据“ASA”时,可添加“∠B=∠D”,故C能判定;
当根据“AAS”时,可添加“∠C=∠E”,故D能判定;
故选B.
【考点】直角三角形全等的判定
【分析】判定两个直角三角形全等的方法有:SAS、SSS、AAS、ASA.HL五种,然后结合题目所给的条件进行判断即可.
解:两直角三角形隐含一个条件是两直角相等,要判定两直角三角形全等,起码还要两个条件,故可排除A.C;
而B构成了AAA,不能判定全等;
D构成了SAS,可以判定两个直角三角形全等.
故答案为:D.
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定方法及“HL”定理,判断即可.
解:①有两条直角边对应相等,可以利用SAS证明全等,正确; ②有两个锐角对应相等,不能利用AAA证明全等,错误;
③有斜边和一条直角边对应相等,可以利用HL证明全等,正确;
④有一条直角边和一个锐角相等,可以利用AAS证明全等,正确;
⑤有斜边和一个锐角对应相等,可以利用AAS证明全等,正确;
⑥有两条边相等,可以利用HL或SAS证明全等,正确;
故选B
【考点】直角三角形全等的判定
【分析】根据三角形全等的判定定理进行分析即可.
解:A.有两个角和一条边对应相等的两个三角形全等,说法正确;
B.有一条边和一个锐角对应相等的两个直角三角形全等,说法正确;
C、有两边和其中一边的对角对应相等的两个三角形全等,说法错误;
D、有两条直角边对应相等的两个直角三角形全等,说法正确;
故选:C
【考点】直角三角形全等的判定
【分析】根据直角三角形的判定进行分析,从而得到答案.
解:A.应为“直角三角形中,已知两直角边的边长为3和4,则斜边的边长为5”,故错误;
B、应为“三角形是直角三角形,三角形的直角边分别为a,b,斜边为c则满足a2﹣b2=c2”,故错误;
C、比如:边长分别为3,4,5,有32+42=25=52 , 能构成直角三角形,故错误;
D、根据三角形内角和定理可求出三个角分别为15°,75°,90°,因而是直角三角形,故正确.
故选D.
【考点】直角三角形全等的判定
【分析】要判断能使两个直角三角形全等的条件首先要看现在有的条件:一对直角对应相等,还需要两个条件,而AAA是不能判定三角形全等的,所以正确的答案只有选项B了.
解:A选项,无法证明两条直角边对应相等,因此A错误.
C、D选项,在全等三角形的判定过程中,必须有边的参与,因此C、D选项错误.
B选项的根据是全等三角形判定中的SAS判定.
故选:B.
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定定理HL、SAS、AAS、ASA分别进行分析即可.
解:①有两个锐角相等的直角三角形全等,说法错误;②一条斜边对应相等的两个直角三角形全等,说法错误;③三个角对应相等的两个三角形全等,说法错误; ④两个直角三角形全等,说法错误.故选:A.
【考点】直角三角形全等的判定
【分析】先证AO为角平分线,再根据直角三角形全等的判别方法HL可证△AOD≌△AOP.
解:∵OD=OP,OD⊥AB且OP⊥AC,
∴AO为角平分线,
∴△ADO和△OPO是直角三角形,
又∵OD=OP且AO=AO
∴△AOD≌△AOP.
故选D.
【考点】直角三角形全等的判定
【分析】△ADO≌△AEO,△DOC≌△EOB,△COF≌△BOF,△ACF≌△ABF,△ADB≌△AEC,△BCE≌△CBD.
利用全等三角形的判定可证明,做题时,要结合已知条件与三角形全等的判定方法逐个验证.
解:∵BD⊥AC,CE⊥AB,∴∠ADB=∠AEC=90°,
∵AC=AB,
∵∠CAE=∠BAD,
∴△AEC≌△ADB;
∴CE=BD,
∵AC=AB,
∴∠CBE=∠BCD,
∵∠BEC=∠CDB=90°,
∴△BCE≌△CBD;
∴BE=CD,
∴AD=AE,
∵AO=AO,
∴△AOD≌△AOE;
∵∠DOC=∠EOB,
∴△COD≌△BOE;
∴OB=OC,
∵AB=AC,
∴CF=BF,AF⊥BC,
∴△ACF≌△ABF,△COF≌△BOF.
共6对,故选D.
二 、填空题
【考点】直角三角形全等的判定
【分析】首先根据三角形的高可得两个高所在的三角形是直角三角形,再根据由已知一组直角边和一组斜边相等,利用直角三角形的判断方法,可得两个直角三角形全等.
解: 因为BE,CD是△ABC的高,所以∠CDB=∠BEC=90°, △CDB和△BEC是直角三角形;且BD=EC,BC=CB所以△BCD≌△CBE;
【考点】直角三角形全等的判定
解:∵∠C=∠D=90°,AB=BA,
∴可以添加AC=BD或BC=AD利用HL判定△ABC≌△BAD;
添加∠ABC=∠BAD或∠CAB=∠DBA利用AAS判定△ABC≌△BAD.
故应填:AC=BD或BC=AD或∠ABC=∠BAD或∠CAB=∠DBA,
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定定理,针对每一个选项进行分析,可得答案.
解:①有两边和一角对应相等的两个三角形不一定全等,错误; ②斜边和一条直角边对应相等的两个直角三角形全等,正确;
③有三角对应相等的两个直角三角形不一定全等,错误;
④有两角和其中一角的对边对应相等的两个三角形全等,正确;
故答案为:②④
【考点】直角三角形全等的判定
【分析】此题是一道开放型的题目,答案不唯一,还可以是BC=BD.
解:条件是AC=AD,∵∠C=∠D=90°,
在Rt△ABC和Rt△ABD中
∴Rt△ABC≌Rt△ABD(HL),
故答案为:AC=AD.
【考点】直角三角形全等的判定
【分析】因为∠ABC=∠ADC=90°,所以△ABC和△ADC为直角三角形,又因为CB=CD,CA=CA,故可根据HL判定Rt△ABC≌Rt△ADC.
解:∵∠ABC=∠ADC=90°,CB=CD,CA=CA
∴Rt△ABC≌Rt△ADC(HL).
故填HL.
【考点】直角三角形全等的判定
【分析】可判定△ADE≌△BCE,从而得出AE=BC,则AB=AD+BC.
解:∵MN∥PQ, AB⊥PQ,
∴AB⊥MN,
∴∠DAE=∠EBC=90°,
在Rt△ADE和Rt△BCE中,
∴△ADE≌△BEC(HL),
∴AE=BC,
∵AD+BC=7,
∴AB=AE+BE=AD+BC=7.
故答案为7.
【考点】直角三角形全等的判定,正方形的判定
【分析】作BF⊥CD交CD的延长线于点F,据条件可证得∠ABE=∠CBF,且由已知∠AEB=∠CFB=90°,AB=BC,所以△ABE≌△CBF,可得BE=BF;四边形ABCD的面积等于新正方形FBED的面积(需证明是正方形),即可得BE=3.
解:过B作BF垂直DC的延长线交于点F,∵∠ABC=∠CDA=90°,BF⊥CD,
∴∠ABE+∠EBC=∠CBF+∠EBC,∴∠ABE=∠CBF;
又∵BE⊥AD,BF⊥DF,且AB=BC,
∴△ABE≌△CBF,即BE=BF;
∵BE⊥AD,∠CDA=90°,BE=BF,
∴四边形BEDF为正方形;
由以上得四边形ABCD的面积等于正方形BEDF的面积,即等于9,
∴BE2=9,即BE=3.
三 、解答题
【考点】直角三角形全等的判定
【分析】由∠1=∠2,根据等角对等边,可得BD=CD;在Rt△ABD和Rt△ACD中,AD是公共边,根据HL定理可判定Rt△ABD≌Rt△ACD,进而得到∠ADB=∠ADC即AD平分∠BDC.
解:∵∠1=∠2∴BD=CD
∵AD=AD
∴Rt△ABD≌Rt△ACD
∴∠ADB=∠ADC
即AD平分∠BDC
【考点】直角三角形的性质,直角三角形全等的判定
【分析】先利用HL判定△CAE≌△EBD,从而得出全等三角形的对应角相等,再利用角与角之间的关系,可以得到线段CE与DE的大小与位置关系为相等且垂直.
解:CE=DE,CE⊥DE,理由如下:
∵AC⊥AB,DB⊥AB,
AC=BE,AE=BD,
∴△CAE≌△EBD.
∴∠CEA=∠D.
∵∠D+∠DEB=90°,
∴∠CEA+∠DEB=90°.
即线段CE与DE的大小与位置关系为相等且垂直.
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定定理AAS进行证明.
解:△ABC≌△ADC.理由如下: ∵AB⊥BC,AD⊥DC,
∴∠B=∠D=90°.
在△ABC与△ADC中,
,
∴△ABC≌△ADC(AAS)
【考点】直角三角形全等的判定
【分析】先由BF=EC得到BC=EF,再根据“HL”判定Rt△ABC≌Rt△DEF.
证明:∵BF=EC,
∴BF+FC=FC+EC,即BC=EF,
∵∠A=∠D=90°,
∴△ABC和△DEF都是直角三角形,
在Rt△ABC和Rt△DEF中,
∴Rt△ABC≌Rt△DEF(HL).
【考点】直角三角形全等的判定
【分析】根据直角三角形全等的判定方法:斜边和一条直角边对应相等的两个直角三角形全等进行分析即可.
解:不正确,
因为AC不是△ABC和△ACD的对应边,故不能判定△ABC≌△ACD.
【考点】直角三角形全等的判定
【分析】根据已知条件BE=CF,由线段的和差,得到BF=CE,根据HL得到Rt△ABF≌Rt△DCE.
证明:∵BE=CF,
∴BE+EF=CF+EF,即BF=CE,
∵∠A=∠D=90°,
∴△ABF与△DCE都为直角三角形,
在Rt△ABF和Rt△DCE中,
BC=CE,AB=CD,
∴Rt△ABF≌Rt△DCE(HL)
【考点】直角三角形全等的判定
【分析】根据全等三角形的判定定理HL证得Rt△ADC≌Rt△CBA,在该全等三角形的对应边相等:DC=BA,然后再由HL来证得Rt△ABE≌Rt△CDF.
解:如图,
在Rt△ADC与Rt△CBA中,
∴Rt△ADC≌Rt△CBA(HL),
∴DC=BA.
又∵BE⊥AC于E,DF⊥AC于F,
∴∠AEB=∠CFD=90°,
在Rt△ABE与Rt△CDF中,
∴Rt△ABE≌Rt△CDF(HL).
【考点】直角三角形全等的判定
【分析】(1)在两个直角三角形中,已知的条件有:AB=BE、BC=DE、∠ABC=∠E=90°,即可由SAS判定两个三角形全等.
(2)根据(1)题证得的全等三角形,可得到∠DBE=∠A,由于∠A.∠BCF互余,所以∠FBC、∠BCF互余,即∠BFC是直角.
(1)证明:∵AB⊥BE,DE⊥BE,
∴∠ABC=∠BED=90°,
在△ABC和△BED中,
∴△ABC≌△BED(SAS);
(2)解:∵△ABC≌△BED,
∴∠DBE=∠CAB,
∵∠ABC=90°,
∴∠CAB+∠ACB=90°.
∴∠DBE+∠ACB=90°.
∴在△BFC中,∠BFC=90°.
版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
