27.2.2相似三角形的性质(课件)
图片预览





文档简介
(共19张PPT)
相似三角形的性质
人教版 九年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
问题1 我们知道,边、角是三角形中重要的几何要素.如果△ABC∽△A'B'C',由相似的定义,我们可以得到它们的边、角之间存在什么样的关系?
答:如果△ABC∽△A'B'C',相似比为k,那么
,∠A=∠A',∠B=∠B',∠C=∠C'.
导入新课
三角形中有各种各样的几何量,除边、角之外还有高、中线、角平分线的长度以及周长与面积等,那么相似三角形的这些几何量之间有什么关系呢?这就是我们这节课要探究的问题.
导入新课
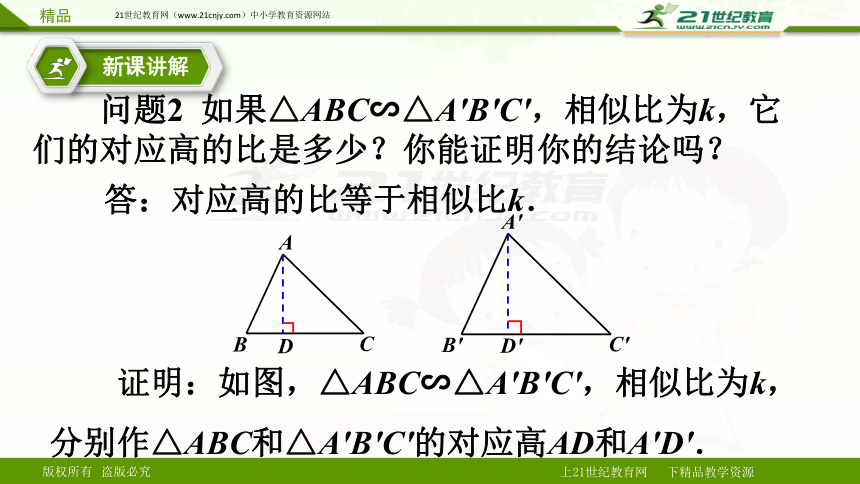
问题2 如果△ABC∽△A'B'C',相似比为k,它们的对应高的比是多少?你能证明你的结论吗?
答:对应高的比等于相似比k.
证明:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应高AD和A'D'.
A′
C′
B′
A
C
B
D
D′
新课讲解
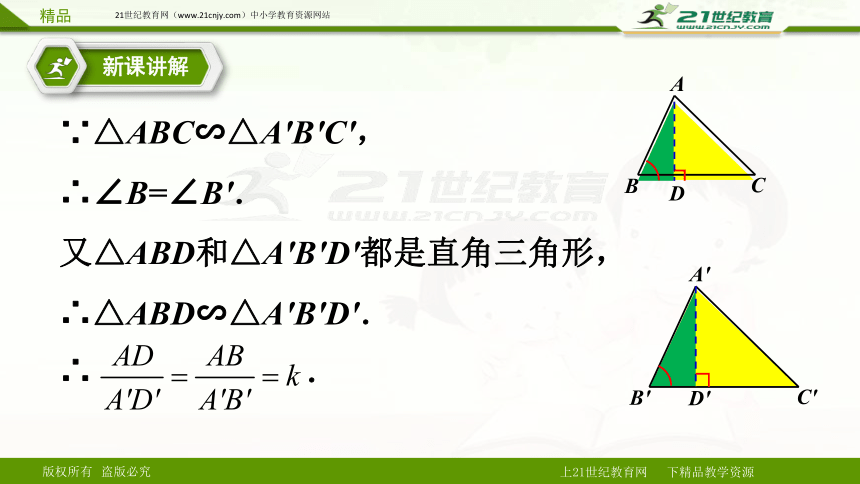
∵△ABC∽△A'B'C',
∴∠B=∠B'.
又△ABD和△A'B'D'都是直角三角形,
∴△ABD∽△A'B'D'.
∴ .
A′
C′
B′
A
C
B
D
D′
新课讲解
问题3 如果△ABC∽△A'B'C',相似比为k,它们的对应中线,对应角平分线的比是否也等于相似比?其他对应线段呢?
答:相似三角形对应中线、对应角平分线的比等于相似比,相似三角形对应线段的比等于相似比.
怎样证明这些结论呢?
新课讲解
证明:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应中线AD和A'D'.
A′
C′
B′
A
C
B
D
D′
新课讲解
∵△ABC∽△A'B'C',
∴∠B=∠B', .
∴在△ABD与△A'B'D'中,△ABD∽△A'B'D'.
∴ .
A′
C′
B′
A
C
B
D
D′
新课讲解
证明:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应角平分线AD和A'D'.
A′
C′
B′
A
C
B
D
D′
新课讲解
∴∠BAD= ∠BAC= ∠B'A'C'=∠B'A'D'.
∴在△ABD与△A'B'D'中,△ABD∽△A'B'D'.
∴ .
∵△ABC∽△A'B'C',
∴∠B=∠B',∠BAC=∠B'A'C'.
∵AD和A'D'分别是∠BAC和∠B'A'C'的平分线,
A′
C′
B′
A
C
B
D
D′
新课讲解
问题4 如果△ABC∽△A'B'C',相似比为k,那么△ABC与△A'B'C'的周长比是多少?
解:∵△ABC∽△A'B'C',相似比为k,
∴AB=kA'B',BC=kB'C',CA=kC'A'.
∴ .
结论:相似三角形周长的比等于相似比.
新课讲解
问题5 如图,△ABC∽△A′B′C′,相似比为k,△ABC与△A′B′C′的面积比是多少?
解: .
相似三角形面积的比等于相似比的平方.
A′
C′
B′
A
C
B
D
D′
新课讲解
例 如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D.若△ABC的边BC上的高为6,面积为 ,求△DEF的边EF上的高和面积.
A
B
C
D
E
F
新课讲解
解:在△ABC和△DEF中,
∵AB=2DE,AC=2DF,
∴ .
又∠D=∠A,
∴△DEF∽△ABC,△DEF与△ABC的相似比为 .
A
B
C
D
E
F
新课讲解
∵△ABC的边BC上的
高为6,面积为 ,
∴△DEF的边EF上
的高为 ,
面积为 .
A
B
C
D
E
F
新课讲解
1.已知△ABC∽△A'B'C',且AB︰A'B'=1︰3,则△ABC与△A'B'C'的周长的比等于( ).
A.1︰3 B.1︰9 C.3︰1 D.9︰1
2.若两个相似三角形的相似比为3︰1,其中较大的三角形的面积为18,则较小的三角形的面积是______.
A
2
巩固练习
1.相似三角形的对应角相等,对应边成比例.
2.相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.一般地,我们有:相似三角形对应线段的比等于相似比.
3.相似三角形周长的比等于相似比.
4.相似三角形面积的比等于相似比的平方.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
相似三角形的性质
人教版 九年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
问题1 我们知道,边、角是三角形中重要的几何要素.如果△ABC∽△A'B'C',由相似的定义,我们可以得到它们的边、角之间存在什么样的关系?
答:如果△ABC∽△A'B'C',相似比为k,那么
,∠A=∠A',∠B=∠B',∠C=∠C'.
导入新课
三角形中有各种各样的几何量,除边、角之外还有高、中线、角平分线的长度以及周长与面积等,那么相似三角形的这些几何量之间有什么关系呢?这就是我们这节课要探究的问题.
导入新课
问题2 如果△ABC∽△A'B'C',相似比为k,它们的对应高的比是多少?你能证明你的结论吗?
答:对应高的比等于相似比k.
证明:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应高AD和A'D'.
A′
C′
B′
A
C
B
D
D′
新课讲解
∵△ABC∽△A'B'C',
∴∠B=∠B'.
又△ABD和△A'B'D'都是直角三角形,
∴△ABD∽△A'B'D'.
∴ .
A′
C′
B′
A
C
B
D
D′
新课讲解
问题3 如果△ABC∽△A'B'C',相似比为k,它们的对应中线,对应角平分线的比是否也等于相似比?其他对应线段呢?
答:相似三角形对应中线、对应角平分线的比等于相似比,相似三角形对应线段的比等于相似比.
怎样证明这些结论呢?
新课讲解
证明:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应中线AD和A'D'.
A′
C′
B′
A
C
B
D
D′
新课讲解
∵△ABC∽△A'B'C',
∴∠B=∠B', .
∴在△ABD与△A'B'D'中,△ABD∽△A'B'D'.
∴ .
A′
C′
B′
A
C
B
D
D′
新课讲解
证明:如图,△ABC∽△A'B'C',相似比为k,分别作△ABC和△A'B'C'的对应角平分线AD和A'D'.
A′
C′
B′
A
C
B
D
D′
新课讲解
∴∠BAD= ∠BAC= ∠B'A'C'=∠B'A'D'.
∴在△ABD与△A'B'D'中,△ABD∽△A'B'D'.
∴ .
∵△ABC∽△A'B'C',
∴∠B=∠B',∠BAC=∠B'A'C'.
∵AD和A'D'分别是∠BAC和∠B'A'C'的平分线,
A′
C′
B′
A
C
B
D
D′
新课讲解
问题4 如果△ABC∽△A'B'C',相似比为k,那么△ABC与△A'B'C'的周长比是多少?
解:∵△ABC∽△A'B'C',相似比为k,
∴AB=kA'B',BC=kB'C',CA=kC'A'.
∴ .
结论:相似三角形周长的比等于相似比.
新课讲解
问题5 如图,△ABC∽△A′B′C′,相似比为k,△ABC与△A′B′C′的面积比是多少?
解: .
相似三角形面积的比等于相似比的平方.
A′
C′
B′
A
C
B
D
D′
新课讲解
例 如图,在△ABC和△DEF中,AB=2DE,AC=2DF,∠A=∠D.若△ABC的边BC上的高为6,面积为 ,求△DEF的边EF上的高和面积.
A
B
C
D
E
F
新课讲解
解:在△ABC和△DEF中,
∵AB=2DE,AC=2DF,
∴ .
又∠D=∠A,
∴△DEF∽△ABC,△DEF与△ABC的相似比为 .
A
B
C
D
E
F
新课讲解
∵△ABC的边BC上的
高为6,面积为 ,
∴△DEF的边EF上
的高为 ,
面积为 .
A
B
C
D
E
F
新课讲解
1.已知△ABC∽△A'B'C',且AB︰A'B'=1︰3,则△ABC与△A'B'C'的周长的比等于( ).
A.1︰3 B.1︰9 C.3︰1 D.9︰1
2.若两个相似三角形的相似比为3︰1,其中较大的三角形的面积为18,则较小的三角形的面积是______.
A
2
巩固练习
1.相似三角形的对应角相等,对应边成比例.
2.相似三角形对应高的比,对应中线的比与对应角平分线的比都等于相似比.一般地,我们有:相似三角形对应线段的比等于相似比.
3.相似三角形周长的比等于相似比.
4.相似三角形面积的比等于相似比的平方.
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
