26.1.2反比例函数的图像和性质 第二课时(课件)
文档属性
| 名称 | 26.1.2反比例函数的图像和性质 第二课时(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.5MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-30 00:00:00 | ||
图片预览







文档简介
(共24张PPT)
人教版 九年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
反比例函数的图象和性质(二)
问题1 下列反比例函数:① ;② ;③ ;④ .
(1)图象位于第一、第三象限的是_________;
(2)图象位于第二、第四象限的是_________.
在回答这个问题之前,我们首先来看下面几个问题:
导入新课
答案:(1)k值分别是①-2;② ;③ ;④ .
(1)上述四个函数中,k值分别是多少?
(2)当k>0时,反比例函数的图象分别位于第几象限?
(3)当k<0时,反比例函数的图象分别位于第几象限?
(2)第一、第三象限.
(3)第二、第四象限.
前面两个问题的答案是:(1)②④;(2)①③.
导入新课
问题2 在反比例函数:① ;② ;
③ ;④ 的图象上,(x1,y1),
(x2,y2)是其图象上同一象限内的点.
(1)若x1<x2,则y1<y2的函数是________;
(2)若x1<x2,则y1>y2的函数是________.
在回答这个问题之前,我们首先来看下面几个问题:
新课讲解
(1)反比例函数 , 的图象位于哪几个象限?y随x的变化趋势是什么?
(2)反比例函数 , 的图象位于哪几个象限?y随x的变化趋势是什么?
新课讲解
答案:
(1)位于第二、第四象限;在每一个象限内,y随x的增大而增大.
(2)位于第一、第三象限;在每一个象限内,y随x的增大而减小.
最后得出前面两个问题的答案是:
(1)①③;(2)②④.
新课讲解
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
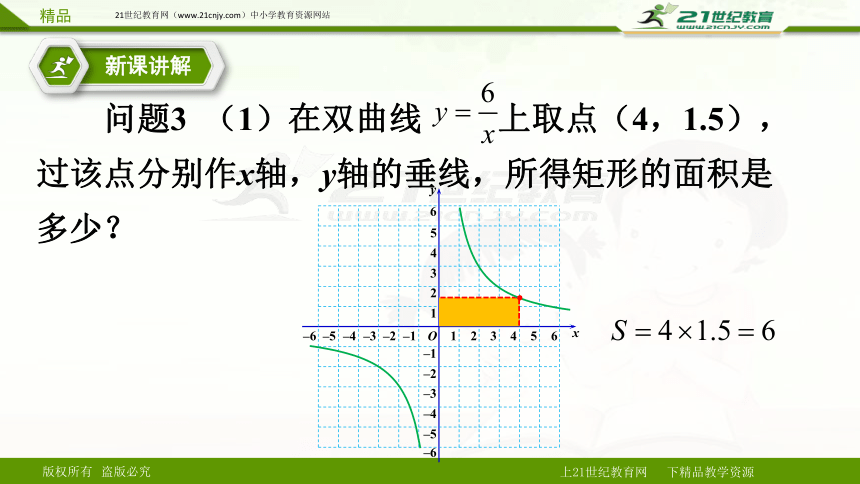
问题3 (1)在双曲线 上取点(4,1.5),过该点分别作x轴,y轴的垂线,所得矩形的面积是多少?
新课讲解
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
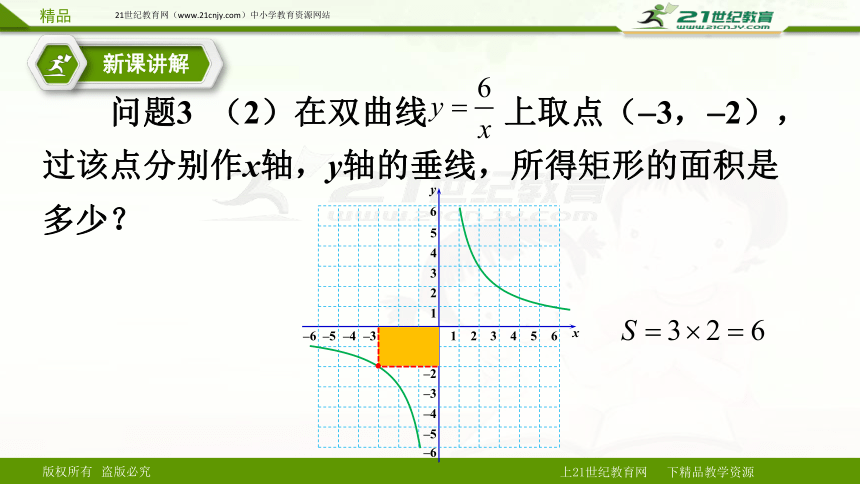
问题3 (2)在双曲线 上取点(-3,-2),过该点分别作x轴,y轴的垂线,所得矩形的面积是多少?
新课讲解
问题3 (3)若点P(a,b)在双曲线 上,过点P分别作x轴,y轴的垂线,所得矩形的面积是多少?
(3)所得矩形的面积 ,即所得矩形的面积等于比例系数k的绝对值.
新课讲解
例1 已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于哪些象限?y随x的增大如何变化?
(2)点B(3,4), ,D(2,5)是否在这个函数的图象上?
我们首先来看下面几个问题:
新课讲解
(1)点A(2,6)在图象上的含义是什么?
(2)图象的位置由哪个量确定?我们如何求出这个量?
(3)反比例函数y随x的变化情况与哪个量有关?y随x的变化情况有没有限制条件?
(4)某点不在图象上的含义是什么?
新课讲解
解:(1)因为点A(2,6)在第一象限,
所以这个函数的图象位于第一、第三象限,在每一个象限内,y随x的增大而减小.
(2)设这个反比例函数的解析式为 ,
因为点A(2,6)在这个函数的图象上,
所以点A的坐标满足 ,即 .
解得k=12.
新课讲解
所以这个反比例函数的解析式为 .
把点B,C,D的坐标代入 ,可知点B,点C的坐标满足函数关系式,点D的坐标不满足函数关系式,
所以点B,点C在函数 的图象上,点D不在这个函数的图象上.
新课讲解
(1)图象的另一支位于哪个象限?
常数m的取值范围是什么?
x
y
例2 如下图,它是反比例函数 的图象的一支,根据图象,回答下列问题:
(2)在这个函数图象的某一支上任取点A(x1,y1),和点B(x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
新课讲解
我们首先来看下面几个问题:
(1)函数图象的一支位于哪个象限?
(2)函数图象所在象限与解析式中哪个量有关?
(3)函数解析式中的系数由哪个式子表示?
(4)在系数范围确定的情况下,在图象的某一支上,y如何随x的大小变化?
新课讲解
解:(1)反比例函数的图象的分布只有两种可能,即位于第一、第三象限,或者位于第二、第四象限.
因为这个函数的图象的一支在第一象限,
所以另一支必位于第三象限.
因为该函数的图象位于第一、第三象限,
所以m-5>0.解得m>5.
新课讲解
(2)因为m-5>0,所以在这个函数图象的任一支上,y都随x的增大而减小,
因此当x1>x2时,y1>y2 .
新课讲解
例3 过反比例函数 的图象上任意
两点A,B分别作x轴的垂线,垂足分别为C,D,连接OA,OB,AC与OB的交点为E, △AOE与梯形ECDB的面积分别为S1,S2,比较它们的大小可得( ).
A.S1>S2 B.S1<S2
C.S1=S2 D.S1,S2的大小关系不能确定
新课讲解
解析:因为S△AOC=S△BOD,
而S△AOC=S△AOE+S△EOC,S△BOD=S△EOC+S梯形ECDB,
所以S△AOE= S梯形ECDB.
答案:C.
新课讲解
1.在函数 的图象上有三点A(x1,y1),B(x2,y2),C(x3,y3),已知x1<x2<0<x3,则y1,y2,y3由小到大的顺序是___________.
y2<y1<y3
2.如图,点A为反比例函数
的图象上一点,AB⊥x轴,S△ABO=2,
则此反比例函数的解析式为
________.
x
y
A
B
O
巩固练习
x
y
P
O
反比例函数 (k为常数,k≠0)中k的几何意义.
(1)过反比例函数图象上的任意一点P作x轴、y轴的垂线,两条垂线与x轴、y轴围成的长方形的面积等于 .
课堂小结
注意:因为反比例函数 (k为常数,k≠0)中的k有正负之分,所以在利用解析式表示
长方形或三角形的面积时,都应加上
绝对值符号.
(2)若点A是反比例函数图象上任意一点,过点A作x轴(或y轴)的垂线,则所作垂线、x轴(或y轴)与线段OA围成的三角形的面积等于 .
x
y
A
P
O
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
人教版 九年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
反比例函数的图象和性质(二)
问题1 下列反比例函数:① ;② ;③ ;④ .
(1)图象位于第一、第三象限的是_________;
(2)图象位于第二、第四象限的是_________.
在回答这个问题之前,我们首先来看下面几个问题:
导入新课
答案:(1)k值分别是①-2;② ;③ ;④ .
(1)上述四个函数中,k值分别是多少?
(2)当k>0时,反比例函数的图象分别位于第几象限?
(3)当k<0时,反比例函数的图象分别位于第几象限?
(2)第一、第三象限.
(3)第二、第四象限.
前面两个问题的答案是:(1)②④;(2)①③.
导入新课
问题2 在反比例函数:① ;② ;
③ ;④ 的图象上,(x1,y1),
(x2,y2)是其图象上同一象限内的点.
(1)若x1<x2,则y1<y2的函数是________;
(2)若x1<x2,则y1>y2的函数是________.
在回答这个问题之前,我们首先来看下面几个问题:
新课讲解
(1)反比例函数 , 的图象位于哪几个象限?y随x的变化趋势是什么?
(2)反比例函数 , 的图象位于哪几个象限?y随x的变化趋势是什么?
新课讲解
答案:
(1)位于第二、第四象限;在每一个象限内,y随x的增大而增大.
(2)位于第一、第三象限;在每一个象限内,y随x的增大而减小.
最后得出前面两个问题的答案是:
(1)①③;(2)②④.
新课讲解
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题3 (1)在双曲线 上取点(4,1.5),过该点分别作x轴,y轴的垂线,所得矩形的面积是多少?
新课讲解
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题3 (2)在双曲线 上取点(-3,-2),过该点分别作x轴,y轴的垂线,所得矩形的面积是多少?
新课讲解
问题3 (3)若点P(a,b)在双曲线 上,过点P分别作x轴,y轴的垂线,所得矩形的面积是多少?
(3)所得矩形的面积 ,即所得矩形的面积等于比例系数k的绝对值.
新课讲解
例1 已知反比例函数的图象经过点A(2,6).
(1)这个函数的图象位于哪些象限?y随x的增大如何变化?
(2)点B(3,4), ,D(2,5)是否在这个函数的图象上?
我们首先来看下面几个问题:
新课讲解
(1)点A(2,6)在图象上的含义是什么?
(2)图象的位置由哪个量确定?我们如何求出这个量?
(3)反比例函数y随x的变化情况与哪个量有关?y随x的变化情况有没有限制条件?
(4)某点不在图象上的含义是什么?
新课讲解
解:(1)因为点A(2,6)在第一象限,
所以这个函数的图象位于第一、第三象限,在每一个象限内,y随x的增大而减小.
(2)设这个反比例函数的解析式为 ,
因为点A(2,6)在这个函数的图象上,
所以点A的坐标满足 ,即 .
解得k=12.
新课讲解
所以这个反比例函数的解析式为 .
把点B,C,D的坐标代入 ,可知点B,点C的坐标满足函数关系式,点D的坐标不满足函数关系式,
所以点B,点C在函数 的图象上,点D不在这个函数的图象上.
新课讲解
(1)图象的另一支位于哪个象限?
常数m的取值范围是什么?
x
y
例2 如下图,它是反比例函数 的图象的一支,根据图象,回答下列问题:
(2)在这个函数图象的某一支上任取点A(x1,y1),和点B(x2,y2).如果x1>x2,那么y1和y2有怎样的大小关系?
新课讲解
我们首先来看下面几个问题:
(1)函数图象的一支位于哪个象限?
(2)函数图象所在象限与解析式中哪个量有关?
(3)函数解析式中的系数由哪个式子表示?
(4)在系数范围确定的情况下,在图象的某一支上,y如何随x的大小变化?
新课讲解
解:(1)反比例函数的图象的分布只有两种可能,即位于第一、第三象限,或者位于第二、第四象限.
因为这个函数的图象的一支在第一象限,
所以另一支必位于第三象限.
因为该函数的图象位于第一、第三象限,
所以m-5>0.解得m>5.
新课讲解
(2)因为m-5>0,所以在这个函数图象的任一支上,y都随x的增大而减小,
因此当x1>x2时,y1>y2 .
新课讲解
例3 过反比例函数 的图象上任意
两点A,B分别作x轴的垂线,垂足分别为C,D,连接OA,OB,AC与OB的交点为E, △AOE与梯形ECDB的面积分别为S1,S2,比较它们的大小可得( ).
A.S1>S2 B.S1<S2
C.S1=S2 D.S1,S2的大小关系不能确定
新课讲解
解析:因为S△AOC=S△BOD,
而S△AOC=S△AOE+S△EOC,S△BOD=S△EOC+S梯形ECDB,
所以S△AOE= S梯形ECDB.
答案:C.
新课讲解
1.在函数 的图象上有三点A(x1,y1),B(x2,y2),C(x3,y3),已知x1<x2<0<x3,则y1,y2,y3由小到大的顺序是___________.
y2<y1<y3
2.如图,点A为反比例函数
的图象上一点,AB⊥x轴,S△ABO=2,
则此反比例函数的解析式为
________.
x
y
A
B
O
巩固练习
x
y
P
O
反比例函数 (k为常数,k≠0)中k的几何意义.
(1)过反比例函数图象上的任意一点P作x轴、y轴的垂线,两条垂线与x轴、y轴围成的长方形的面积等于 .
课堂小结
注意:因为反比例函数 (k为常数,k≠0)中的k有正负之分,所以在利用解析式表示
长方形或三角形的面积时,都应加上
绝对值符号.
(2)若点A是反比例函数图象上任意一点,过点A作x轴(或y轴)的垂线,则所作垂线、x轴(或y轴)与线段OA围成的三角形的面积等于 .
x
y
A
P
O
课堂小结
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
