26.1.2反比例函数的图像和性质 第一课时(课件)
文档属性
| 名称 | 26.1.2反比例函数的图像和性质 第一课时(课件) |

|
|
| 格式 | pptx | ||
| 文件大小 | 4.0MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-30 00:00:00 | ||
图片预览






文档简介
(共25张PPT)
反比例函数的图象和性质(一)
人教版 九年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
问题1 一次函数y=2x-3的图象是什么?它经过哪些象限?你能画出它的图象吗?说一说一次函数y=2x-3具有什么性质?
答:一次函数y=2x-3的图象是一条直线;它经过第一、三、四象限;过点(0,-3)、(2,1)作直线,所得直线就是一次函数y=2x-3的图象;函数y随x的增大而增大……
上节课我们学习了反比例函数,你知道反比例函数 的图象是什么吗?这节课我们就一起来探讨反比例函数的图象和性质.
问题2 猜一猜反比例函数 的图象经过哪些象限?
答:从比例系数k=6=xy,得x,y同号且不为零,说明该函数图象经过第一、三象限,且该函数图象与坐标轴没有交点.
从上图可以看出,只描出三五个点不能看出函数图象的形状.
追问1 我们描出三五个点能看出图象是什么
形状吗?
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
(1,6)
(2,3)
(3,2)
追问2 在(1,6)与(2,3)两点之间的点如(1.5,4)在什么位置?这三点共线吗?
点(1.5,4)的位置比点(1,6)低,比点(2,3)高,这三点不共线.
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
(1,6)
(2,3)
(3,2)
(1.5,4)
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
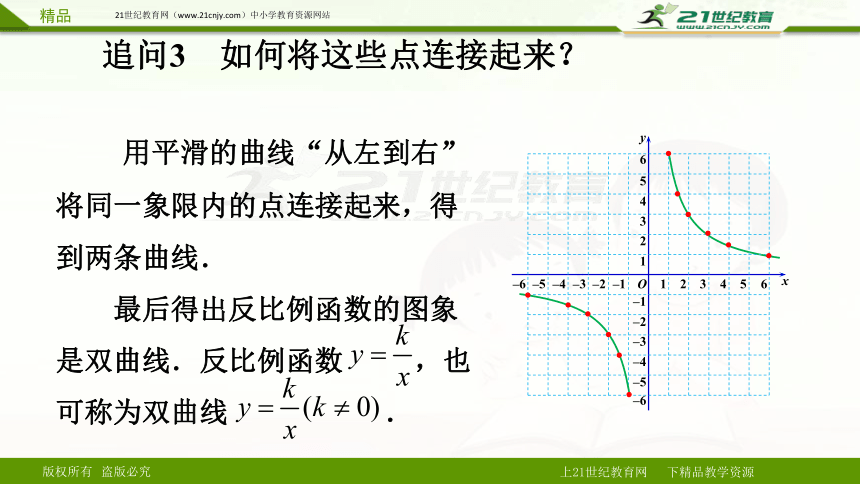
追问3 如何将这些点连接起来?
用平滑的曲线“从左到右”将同一象限内的点连接起来,得到两条曲线.
最后得出反比例函数的图象是双曲线.反比例函数 ,也可称为双曲线 .
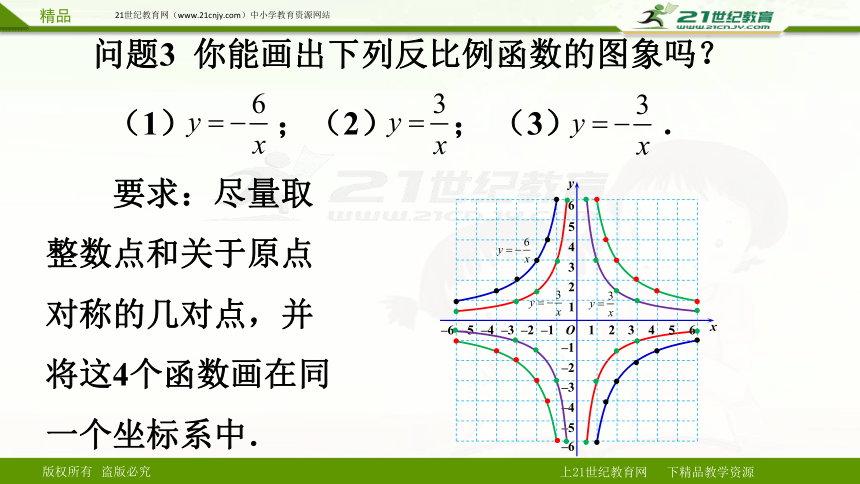
问题3 你能画出下列反比例函数的图象吗?
(1) ;(2) ; (3) .
要求:尽量取整数点和关于原点对称的几对点,并将这4个函数画在同一个坐标系中.
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
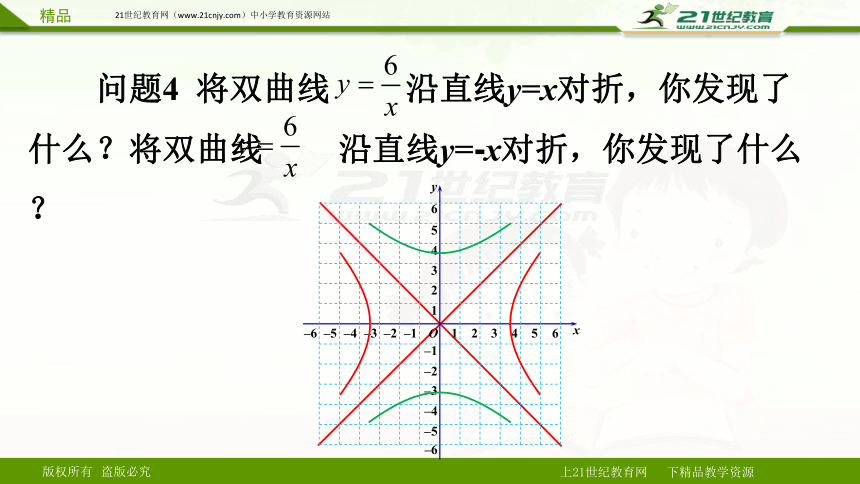
问题4 将双曲线 沿直线y=x对折,你发现了什么?将双曲线 沿直线y=-x对折,你发现了什么?
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题4 将双曲线 沿直线y=x对折,你发现了什么?将双曲线 沿直线y=-x对折,你发现了什么?
发现:双曲线 沿直线y=x对折后互相重合,双曲线 沿直线y=-x对折后也互相重合
结论:双曲线是轴对称图形,它有两条对称轴,分别是直线y=x和直线y=-x.
问题5 点(1,6)和点(6,1)的位置有什么关系?在双曲线上你还能找出类似的对应点吗?点(1,6)和点(-1,-6)具有什么位置关系?在双曲线上你还能找出类似的对应点吗?
答:点(1,6)和点(6,1)关于直线y=x对称,还能找出很多类似的对应点;点(1,6)和点(-6,-1)关于直线y=-x对称,还能找出很多类似的对应点.
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题6 点(1,6)和点(-1,-6)有什么位置关系?在双曲线上你还能找出类似的对应点吗?
答:这两点关于原点对称,像这样的对应点还有很多,这说明双曲线关于原点对称,即双曲线是中心对称图形.
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题7 从左向右观察双曲线上的点(1,6)、(2,3)、
(3,2),横坐标在怎样变化?纵坐标又是怎样变化的?从左向右观察双曲线上的点(-3,-2)、(-2,-3)、(1,6),横坐标在怎样变化?纵坐标又是怎样变化的?
横坐标在增大,而纵坐标在减小(y值随x值的增大而减小);横坐标在增大,而纵坐标先减小后增大.(看图象)
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题8 对于反比例函数 ,
(1)当k>0时,图象的双支分别位于哪些象限?y值随x值的变化怎样变化?
(2)又若k<0呢?
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
(1)当k>0时,x,y同号,所以双曲线的两支分别位于第一、第三象限,在每一个象限内,y值随x值的增大而减小;
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
(2)当k<0时,x,y异号,所以双曲线的两支分别位于第二、第四象限,在每一个象限内,y值随x值的增大而增大.
例 已知反比例函数 ,当x<0时,y
随x的增大而减小,求正整数m的值.
解:因为反比例函数 ,
当x<0时,y随x的增大而减小,
所以3-2m>0.解得 .
所以正整数m的值是1.
一次函数y=x+m(m≠0)与反比例函数 在同一平面直角坐标系中的图象大致是( ).
B
x
y
x
y
x
y
x
y
B
A
C
D
O
O
O
O
1.一般地,反比例函数 的图象是双曲线,它具有以下性质:
(1)当k>0时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y随x的增大而减小;
(2)当k<0时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y随x的增大而增大.
2.反比例函数的图象是轴对称图形,对称轴是直线y=x或y=-x;
反比例函数的图象也是中心对称图形,对称中心是坐标原点.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
反比例函数的图象和性质(一)
人教版 九年级下
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
问题1 一次函数y=2x-3的图象是什么?它经过哪些象限?你能画出它的图象吗?说一说一次函数y=2x-3具有什么性质?
答:一次函数y=2x-3的图象是一条直线;它经过第一、三、四象限;过点(0,-3)、(2,1)作直线,所得直线就是一次函数y=2x-3的图象;函数y随x的增大而增大……
上节课我们学习了反比例函数,你知道反比例函数 的图象是什么吗?这节课我们就一起来探讨反比例函数的图象和性质.
问题2 猜一猜反比例函数 的图象经过哪些象限?
答:从比例系数k=6=xy,得x,y同号且不为零,说明该函数图象经过第一、三象限,且该函数图象与坐标轴没有交点.
从上图可以看出,只描出三五个点不能看出函数图象的形状.
追问1 我们描出三五个点能看出图象是什么
形状吗?
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
(1,6)
(2,3)
(3,2)
追问2 在(1,6)与(2,3)两点之间的点如(1.5,4)在什么位置?这三点共线吗?
点(1.5,4)的位置比点(1,6)低,比点(2,3)高,这三点不共线.
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
(1,6)
(2,3)
(3,2)
(1.5,4)
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
追问3 如何将这些点连接起来?
用平滑的曲线“从左到右”将同一象限内的点连接起来,得到两条曲线.
最后得出反比例函数的图象是双曲线.反比例函数 ,也可称为双曲线 .
问题3 你能画出下列反比例函数的图象吗?
(1) ;(2) ; (3) .
要求:尽量取整数点和关于原点对称的几对点,并将这4个函数画在同一个坐标系中.
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题4 将双曲线 沿直线y=x对折,你发现了什么?将双曲线 沿直线y=-x对折,你发现了什么?
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题4 将双曲线 沿直线y=x对折,你发现了什么?将双曲线 沿直线y=-x对折,你发现了什么?
发现:双曲线 沿直线y=x对折后互相重合,双曲线 沿直线y=-x对折后也互相重合
结论:双曲线是轴对称图形,它有两条对称轴,分别是直线y=x和直线y=-x.
问题5 点(1,6)和点(6,1)的位置有什么关系?在双曲线上你还能找出类似的对应点吗?点(1,6)和点(-1,-6)具有什么位置关系?在双曲线上你还能找出类似的对应点吗?
答:点(1,6)和点(6,1)关于直线y=x对称,还能找出很多类似的对应点;点(1,6)和点(-6,-1)关于直线y=-x对称,还能找出很多类似的对应点.
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题6 点(1,6)和点(-1,-6)有什么位置关系?在双曲线上你还能找出类似的对应点吗?
答:这两点关于原点对称,像这样的对应点还有很多,这说明双曲线关于原点对称,即双曲线是中心对称图形.
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题7 从左向右观察双曲线上的点(1,6)、(2,3)、
(3,2),横坐标在怎样变化?纵坐标又是怎样变化的?从左向右观察双曲线上的点(-3,-2)、(-2,-3)、(1,6),横坐标在怎样变化?纵坐标又是怎样变化的?
横坐标在增大,而纵坐标在减小(y值随x值的增大而减小);横坐标在增大,而纵坐标先减小后增大.(看图象)
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
问题8 对于反比例函数 ,
(1)当k>0时,图象的双支分别位于哪些象限?y值随x值的变化怎样变化?
(2)又若k<0呢?
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
(1)当k>0时,x,y同号,所以双曲线的两支分别位于第一、第三象限,在每一个象限内,y值随x值的增大而减小;
x
–1
–2
–3
–4
–5
1
2
3
4
5
–1
–2
–3
–4
–5
1
2
3
4
5
O
–6
6
y
–6
6
(2)当k<0时,x,y异号,所以双曲线的两支分别位于第二、第四象限,在每一个象限内,y值随x值的增大而增大.
例 已知反比例函数 ,当x<0时,y
随x的增大而减小,求正整数m的值.
解:因为反比例函数 ,
当x<0时,y随x的增大而减小,
所以3-2m>0.解得 .
所以正整数m的值是1.
一次函数y=x+m(m≠0)与反比例函数 在同一平面直角坐标系中的图象大致是( ).
B
x
y
x
y
x
y
x
y
B
A
C
D
O
O
O
O
1.一般地,反比例函数 的图象是双曲线,它具有以下性质:
(1)当k>0时,双曲线的两支分别位于第一、第三象限,在每一个象限内,y随x的增大而减小;
(2)当k<0时,双曲线的两支分别位于第二、第四象限,在每一个象限内,y随x的增大而增大.
2.反比例函数的图象是轴对称图形,对称轴是直线y=x或y=-x;
反比例函数的图象也是中心对称图形,对称中心是坐标原点.
谢 谢!
21世纪教育网(www.21cnjy.com)中小学教育资源及组卷应用平台
有大把优质资料?一线名师?一线教研员?赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
