13.2.2用坐标表示轴对称教案
图片预览



文档简介
用坐标表示轴对称
教学目标
(一)教学知识点
1.在平面直角坐标系中,探索关于x轴、y轴对称的点的坐标规律.
2.利用关于x轴、y轴对称的点的坐标的规律,能作出关于x轴、y轴对称的图形.
(二)能力训练要求
1.在探索关于x轴,y轴对称的点的坐标的规律时,发展学生数形结合的思维意识.
2.在同一坐标系中,感受图形上点的坐标的变化与图形的轴对称变换之间的关系.
(三)情感与价值观要求
在探索规律的过程中,提高学生的求知欲和强烈的好奇心.
教学重点
1.理解图形上的点的坐标的变化与图形的轴对称变换之间的关系.
2.在用坐标表示轴对称时发展形象思维能力和数形结合的意识.
教学难点
用坐标表示轴对称.
教学方法
探索发现法.
教具准备
课件,坐标纸.
教学过程
Ⅰ.提出问题,创设情境
[活动1]
1.如图:
(1)观察上图中两个圆脸有什么关系?
(2)已知右边图脸右眼的坐标为(4,3),左眼的坐标为(2,3),嘴角两个端点,右端点的坐标为(4,1),左端点的坐标为(2,1).
你能根据轴对称的性质写出左边圆脸上左眼,右眼及嘴角两端点的坐标吗?
2.在平面直角坐标系中,将坐标为(2,2),(4,2),(4,4),(2,4),(2,2)的点用线段依次连结起来形成一个图案.
(1)纵坐标不变,横坐标分别乘以-1,再将所得的各个点用线段依次连结起来,所得的图案与原图案相比有何变化?
(2)横坐标不变,纵坐标分别乘以-1,再将所得的各个点用线段依次连结起来,所得的图案又与原图案相比有何变化?
设计意图:
通过有趣的轴对称图形的研究,激发学生探究坐标特点的好奇心,是一种形到数的探究,接着又从对坐标实施变化,引起图案的变化,使学生在坐标的变化中产生对每对关于x轴、y轴对称的点的坐标规律的探究.
师生行为:
[生]1.(1)观察可发现图中的两个圆脸关于y轴对称.
(2)我们可以设右脸中的左眼为A点,右眼为B点,则A(2,3),B(4,3),嘴角的左右端为D(2,1),C(4,1).根据轴对称的性质,A与A1关于y轴对称,则A1到y轴的距离和A到y轴的距离相等,A1、A到x轴的距离也相等,∵A1在第二象限,∴A1的坐标为(-2,3).
同理,B1、C1、D1的坐标分别为(-4,3)、(-4,1)、(-2,1).
2.师生共同完成
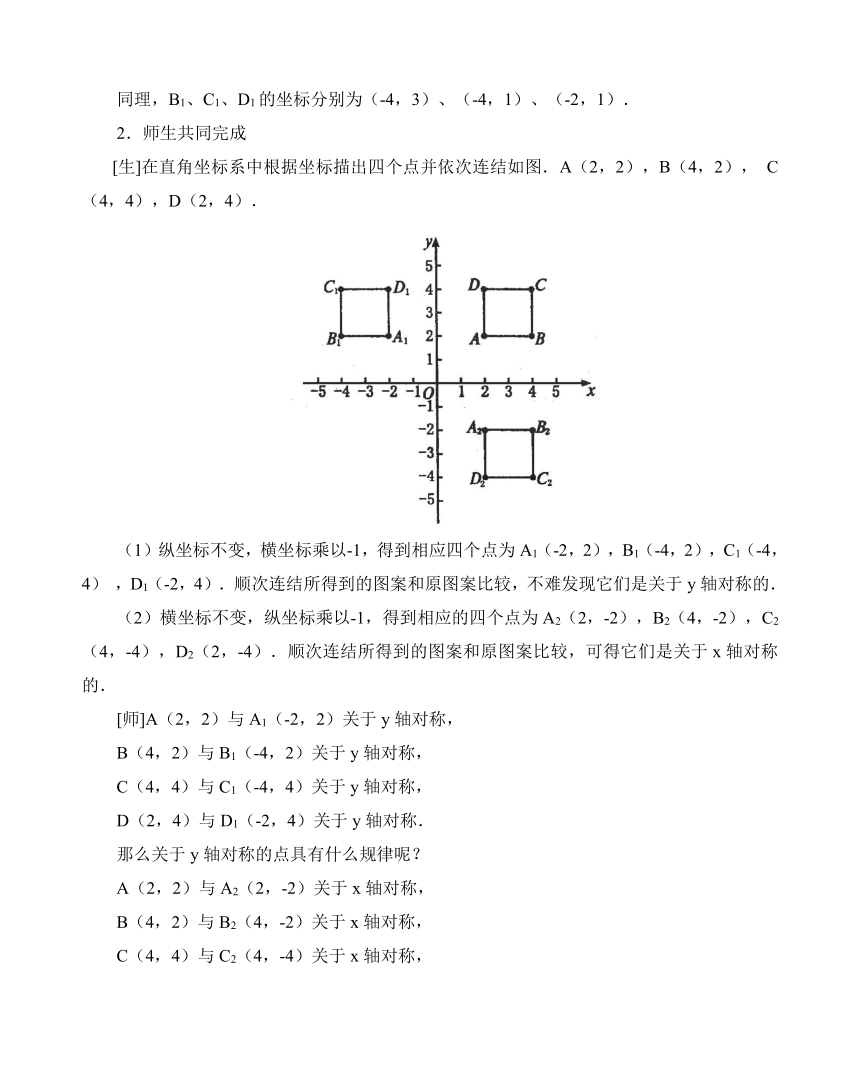
[生]在直角坐标系中根据坐标描出四个点并依次连结如图.A(2,2),B(4,2),C(4,4),D(2,4).
(1)纵坐标不变,横坐标乘以-1,得到相应四个点为A1(-2,2),B1(-4,2),C1(-4,4),D1(-2,4).顺次连结所得到的图案和原图案比较,不难发现它们是关于y轴对称的.
(2)横坐标不变,纵坐标乘以-1,得到相应的四个点为A2(2,-2),B2(4,-2),C2(4,-4),D2(2,-4).顺次连结所得到的图案和原图案比较,可得它们是关于x轴对称的.
[师]A(2,2)与A1(-2,2)关于y轴对称,
B(4,2)与B1(-4,2)关于y轴对称,
C(4,4)与C1(-4,4)关于y轴对称,
D(2,4)与D1(-2,4)关于y轴对称.
那么关于y轴对称的点具有什么规律呢?
A(2,2)与A2(2,-2)关于x轴对称,
B(4,2)与B2(4,-2)关于x轴对称,
C(4,4)与C2(4,-4)关于x轴对称,
D(2,4)与D2(2,-4)关于x轴对称.
那么关于x轴对称的点有何规律呢?
这节课我们就来研究关于x轴,y轴对称的每对对称点坐标的规律.
Ⅱ.导入新课
[活动2]
在如图所示的平面坐标系中,画出下列已知点及其对称点,并把坐标填入表格中.看看每对对称点的坐标有怎样的规律.再和同学讨论一下.
已知点A(2,-3),B(-1,2),C(-6,-5),D(,1),E(4,0).
关于x轴的对称点A′(____,____)B′(_____,______)C′(_____,_____)D′(____,_____)E′(_____,_____).
关于y轴的对称点A″(_____,____)B″(_____,______)C″(_____,_____)D″(____,_____)E″(_____,_____).
设计意图:
通过学生动手操作,分别作A,B,C,D,E关于x轴、y轴的对称点A′,B′,C′,D′,E′;A″,B″,C″,D″,E″,并且求出它们的坐标,观察,归纳它们坐标之间的关系.
师生行为:
教师引导,学生自主探索发现关于x轴、y轴对称的每组对称点坐标的规律.
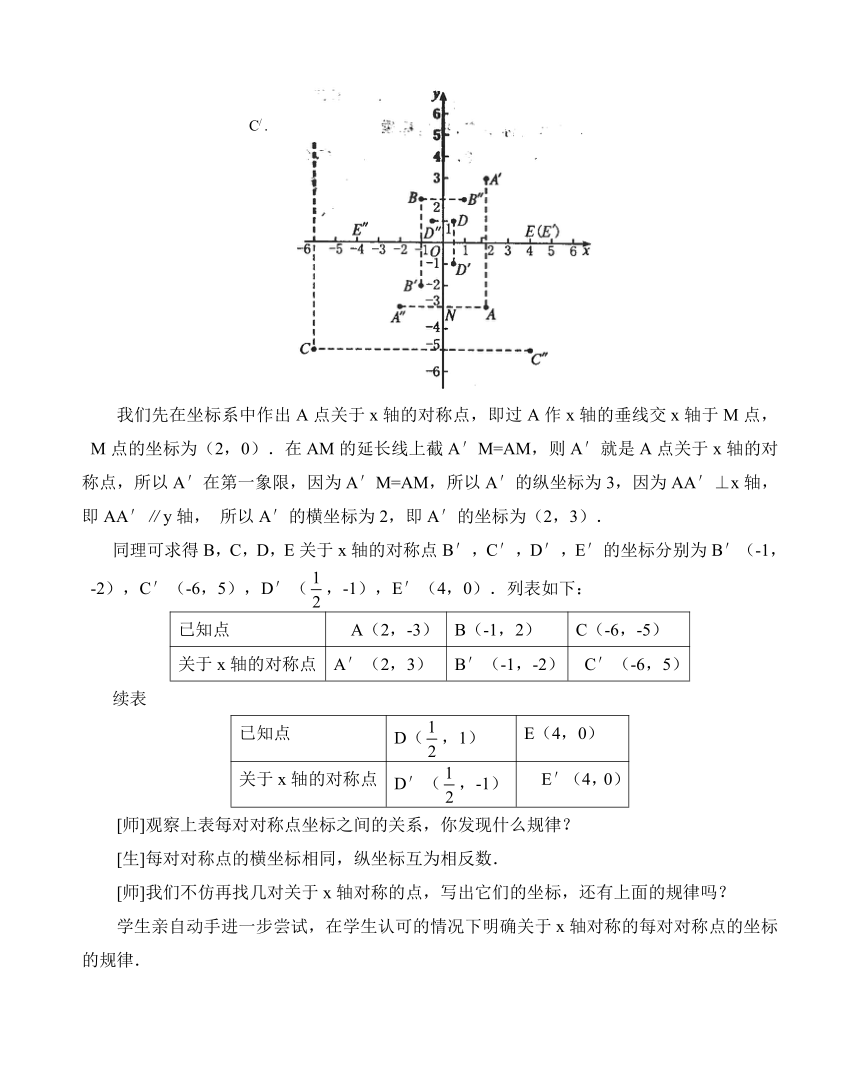
[生]如图,我们先在直角坐标系中描出A(2,-3),B(-1,2),C(-6,-5),D(,1),E(4,0)点.
我们先在坐标系中作出A点关于x轴的对称点,即过A作x轴的垂线交x轴于M点,M点的坐标为(2,0).在AM的延长线上截A′M=AM,则A′就是A点关于x轴的对称点,所以A′在第一象限,因为A′M=AM,所以A′的纵坐标为3,因为AA′⊥x轴,即AA′∥y轴,所以A′的横坐标为2,即A′的坐标为(2,3).
同理可求得B,C,D,E关于x轴的对称点B′,C′,D′,E′的坐标分别为B′(-1,-2),C′(-6,5),D′(,-1),E′(4,0).列表如下:
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
关于x轴的对称点
A′(2,3)
B′(-1,-2)
C′(-6,5)
续表
已知点
D(,1)
E(4,0)
关于x轴的对称点
D′(,-1)
E′(4,0)
[师]观察上表每对对称点坐标之间的关系,你发现什么规律?
[生]每对对称点的横坐标相同,纵坐标互为相反数.
[师]我们不仿再找几对关于x轴对称的点,写出它们的坐标,还有上面的规律吗?
学生亲自动手进一步尝试,在学生认可的情况下明确关于x轴对称的每对对称点的坐标的规律.
[师生共析]
关于x轴对称的每对对称点的坐标:横坐标相同,纵坐标互为相反数.
接着我们再来作出A,B,C,D,E关于y轴的对称点,并求出它们的坐标.
[生]同样,我们先作出A关于y轴的对称点A″,并求出A″的坐标.
过A作y轴的垂线AN,垂足为N,则N点坐标为(0,-3),然后在AN的延长线上截A″N,使A″N=AN,则A″就是所求的A关于y轴的对称点.A″在第三象限,AA″⊥y轴,且AN=A″N,所以A″的坐标为(-2,-3),同理可求得B,C,D,E关于y轴的对称点B″,C″,D″,E″的坐标分别为B″(1,2),C″(6,-5),D″(-,1),E″(-4,0).列表如下:
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
关于y轴对称点
A″(-2,-3)
B″(1,2)
C″(6,-5)
续表
已知点
D(,1)
E(4,0)
关于y轴对称点
D″(,1)
E″(-4,0)
[师]观察上表,比较每对关于y轴的对称点的坐标,你能发现什么规律?
[生]关于y轴对称的每一对对称点的坐标纵坐标相同,横坐标互为相反数.
Ⅲ.随堂练习
[活动3]
练习:(教科书P41练习)
1.分别写出下列各点关于x轴和y轴对称的点的坐标:
(-2,6),(1,-2),(-1,3),(-4,-2),(1,0).
2.如图,△ABC关于x轴对称,点A的坐标为(1,-2),标出点B的坐标.
3.如图,利用关于坐标轴对称的点的坐标的特点,分别作出与△ABC关于x轴和y轴对称的图形.
设计意图:
巩固关于x轴、y轴对称的每对对称点的坐标规律.根据已知点,能求出关于x轴、y轴对称的点的坐标,并能利用关于坐标轴对称的点的坐标特点,作出与已知图形关于坐标轴对称的图形.
师生行为:
学生练习,教师巡视,师生共评.
[生]1.解:根据关于x轴对称的点的坐标的特点求得(-2,6),(1,-2),(-1,3),(-4,-2),(1,0)关于x轴对称的点的坐标分别为(-2,-6),(1,2),(-1,-3),(-4,2),(1,0).
根据关于y轴对称的点的坐标的特点可得(-2,6),(1,-2),(-1,3),(-4,-2),(1,0)关于y轴对称的点的坐标分别为(2,6),(-1,-2),(1,3),(4,-2),(-1,0).
2.△ABC关于x轴对称,则A、B为关于x轴的一对对称点,已知A的坐标为(1,-2),则B的坐标为(1,2).
3.分析:要作出与△ABC关于x轴、y轴的对称图形,只需把A、B、C关于x轴、y轴的对称点找到即可.
解:△ABC各顶点的坐标:A(-4,1),B(-1,-1),C(-3,2)它们关于x轴对称的点的坐标为A1(-4,-1),B1(-1,1),C1(-3,-2).在同一直角坐标系中描出A1(-4,-1),B1(-1,1),C1(-3,-2)连结A1B1,B1C1,C1A1,则△A1B1C1就是△ABC关于x轴对称的图形(如图).
A(-4,1),B(-1,-1),C(-3,2)它们关于y轴对称的点的坐标为A2(4,1),B2(1,-1),C2(3,2).在同一坐标系中描出A2(4,1),B2(1,-1),C2(3,2),连结A2B2,B2C2,C2A2,则△A2B2C2就是△ABC关于y轴对称的图形(如图).
[活动4]
补充练习:
1.将下图中的点(2,1),(5,1),(2,5)做如下变化:
(1)纵坐标不变,横坐标分别加2.
(2)横坐标不变,纵坐标分别加1.
(3)纵坐标不变,横坐标分别变为原来的2倍.
(4)横坐标不变,纵坐标分别变为原来的2倍.
(5)纵坐标不变,横坐标分别乘以-1.
(6)横坐标不变,纵坐标分别乘以-1.
(7)纵坐标、横都分别乘以-1,观察变化后的三角形与原三角形有什么变化?
设计意图:
进一步让同学们亲身经历点的坐标的变化与图形变换之间的关系.
师生行为:
学生练习,教师指导.
精析:行根据变化,把每次变化后的三个顶点坐标求出,在平面直角坐标系中描出它们,连结成新三角形,然后与原有的三角形进行比较.
精解:(1)纵坐标不变,横坐标分别加2得三个点依次为(4,1),(7,1),(4,5).将各点用线段依次连结起来,所得图形如图(1)所示,与原图形相比三角形的形状、大小不变,整个三角形向右平移了2个单位长度.
(2)横坐标不变,纵坐标分别加1,得三个点依次为(2,2),(5,2),(2,6).将各点用线段依次连结起来,所得图形如图(2)所示,与原图形相比,三角形的形状、大小不变,整个三角形向上平移了1个单位长度.
(3)纵坐标不变,横坐标分别变为原来的2倍,得三个点依次为(4,1),(10,1),(4,5).将各点用线段依次连结起来,所得图形如图(3)所示,与原图形相比,整个三角形被横向拉长为原来的2倍.
(4)横坐标不变,纵坐标分别变为原来的2倍,得三个点依次为(2,2),(5,2),(2,10).将各点依次用线段连结起来,所得图形如图(4)所示,与原图形相比,整个三角形被纵向拉长2倍.
(5)纵坐标不变,横坐标分别乘以-1,得三个点坐标为(-2,1),(-5,1),(-2,5).将各点依次用线段连结起来,如图(5)所示,与原图形相比,三角形的形状、大小不变,整个三角形与原三角形关于y轴对称.
(6)横坐标不变,纵坐标分别乘以-1,得三个点坐标为(2,-1),(5,-1),(2,-5).将各点用线段连结起来,如图(6)所示,与原图形相比,三角形的形状、大小不变,整个三角形与原三角形关于x轴对称.
(7)横纵坐标都分别乘以-1,得三个点坐标为(-2,-1),(-5,-1),(-2,-5).将各点用线段依次连结起来,如图(7)所示,与原图形相比,整个三角形的形状、大小不变,整个三角形与原三角形关于O点对称.
Ⅳ.课时小结
本节课的主要内容(由学生在教师的引导下共同回忆总结):
1.在直角坐标系中,探索了关于x轴,y轴对称的对称点坐标规律.
2.利用关于坐标轴对称的点的坐标的特点,作已知图形的轴对称图形,体现了数形结合的数学思想.
Ⅴ.课后作业
教科书习题12.2─2、3、4题,第6题、第7题(学有余力的同学做).
Ⅵ.活动与探究
如下图,以树干为对称轴,画出树的另一半.
分析:要画出树的另一半,根据轴对称图形的性质,关于对称轴对称的对应点的横坐标是互为相反数,纵坐标不变,因此需要在图中先建立直角坐标系,写出对称轴左侧某些点的坐标,然后对称地写出右侧的对应点的坐标,再进行连结.
解:如上图所示建立直角坐标系,对称轴为y轴,y轴左侧的点A、C两点的坐标为(-4,0)、(-3,4),对称点A′、C′的坐标为(4,0)、(3,4),O、B、D三点都在对称轴上,然后用线段连结起来.
2.A、B、C、D、E各点的坐标如下图所示,确定△ABE、△EBD、△ABC的面积,你是怎样做的?你发现了什么规律?
解:A、B、C、D、E各点的坐标分别为A(0,6),B(0,3),C(6,1),D(-2,-2),E(-8,0).
△ABE的面积为(8×6-8×3)=12.
△EBD的面积为8×5- ×8×3- ×2×5- ×6×2=17.
△ABC的面积为(6×5-2×6)=9.
规律为可以将每个三角形的面积看成边与坐标轴平行的矩形的一半.
板书设计
§12.2.2 用坐标表示轴对称
一、探索关于x轴、y轴对称的每对对称点的规律.
(1)关于x轴对称的点的坐标横坐标相同,纵坐标互为相反数.
(2)关于y轴对称的点的坐标纵坐标相同,横坐标互为相反数.
二、利用关于x轴、y轴对称的点的坐标的规律,能作出关于x轴、y轴对称的图形.
备课资料
(一)参考练习
1.已知A点坐标为(-1,3).
(1)与点A关于y轴对称的点坐标.
(2)与点A关于x轴对称的点坐标.
2.已知△ABC的顶点坐标分别为(3,3),(2,1),(4,1).请你在同一坐标系中作出:
(1)关于x轴对称的图形.
(2)关于y轴对称的图形.
3.描出图中的枫叶图案关于x轴的轴对称图形的简图.
教学目标
(一)教学知识点
1.在平面直角坐标系中,探索关于x轴、y轴对称的点的坐标规律.
2.利用关于x轴、y轴对称的点的坐标的规律,能作出关于x轴、y轴对称的图形.
(二)能力训练要求
1.在探索关于x轴,y轴对称的点的坐标的规律时,发展学生数形结合的思维意识.
2.在同一坐标系中,感受图形上点的坐标的变化与图形的轴对称变换之间的关系.
(三)情感与价值观要求
在探索规律的过程中,提高学生的求知欲和强烈的好奇心.
教学重点
1.理解图形上的点的坐标的变化与图形的轴对称变换之间的关系.
2.在用坐标表示轴对称时发展形象思维能力和数形结合的意识.
教学难点
用坐标表示轴对称.
教学方法
探索发现法.
教具准备
课件,坐标纸.
教学过程
Ⅰ.提出问题,创设情境
[活动1]
1.如图:
(1)观察上图中两个圆脸有什么关系?
(2)已知右边图脸右眼的坐标为(4,3),左眼的坐标为(2,3),嘴角两个端点,右端点的坐标为(4,1),左端点的坐标为(2,1).
你能根据轴对称的性质写出左边圆脸上左眼,右眼及嘴角两端点的坐标吗?
2.在平面直角坐标系中,将坐标为(2,2),(4,2),(4,4),(2,4),(2,2)的点用线段依次连结起来形成一个图案.
(1)纵坐标不变,横坐标分别乘以-1,再将所得的各个点用线段依次连结起来,所得的图案与原图案相比有何变化?
(2)横坐标不变,纵坐标分别乘以-1,再将所得的各个点用线段依次连结起来,所得的图案又与原图案相比有何变化?
设计意图:
通过有趣的轴对称图形的研究,激发学生探究坐标特点的好奇心,是一种形到数的探究,接着又从对坐标实施变化,引起图案的变化,使学生在坐标的变化中产生对每对关于x轴、y轴对称的点的坐标规律的探究.
师生行为:
[生]1.(1)观察可发现图中的两个圆脸关于y轴对称.
(2)我们可以设右脸中的左眼为A点,右眼为B点,则A(2,3),B(4,3),嘴角的左右端为D(2,1),C(4,1).根据轴对称的性质,A与A1关于y轴对称,则A1到y轴的距离和A到y轴的距离相等,A1、A到x轴的距离也相等,∵A1在第二象限,∴A1的坐标为(-2,3).
同理,B1、C1、D1的坐标分别为(-4,3)、(-4,1)、(-2,1).
2.师生共同完成
[生]在直角坐标系中根据坐标描出四个点并依次连结如图.A(2,2),B(4,2),C(4,4),D(2,4).
(1)纵坐标不变,横坐标乘以-1,得到相应四个点为A1(-2,2),B1(-4,2),C1(-4,4),D1(-2,4).顺次连结所得到的图案和原图案比较,不难发现它们是关于y轴对称的.
(2)横坐标不变,纵坐标乘以-1,得到相应的四个点为A2(2,-2),B2(4,-2),C2(4,-4),D2(2,-4).顺次连结所得到的图案和原图案比较,可得它们是关于x轴对称的.
[师]A(2,2)与A1(-2,2)关于y轴对称,
B(4,2)与B1(-4,2)关于y轴对称,
C(4,4)与C1(-4,4)关于y轴对称,
D(2,4)与D1(-2,4)关于y轴对称.
那么关于y轴对称的点具有什么规律呢?
A(2,2)与A2(2,-2)关于x轴对称,
B(4,2)与B2(4,-2)关于x轴对称,
C(4,4)与C2(4,-4)关于x轴对称,
D(2,4)与D2(2,-4)关于x轴对称.
那么关于x轴对称的点有何规律呢?
这节课我们就来研究关于x轴,y轴对称的每对对称点坐标的规律.
Ⅱ.导入新课
[活动2]
在如图所示的平面坐标系中,画出下列已知点及其对称点,并把坐标填入表格中.看看每对对称点的坐标有怎样的规律.再和同学讨论一下.
已知点A(2,-3),B(-1,2),C(-6,-5),D(,1),E(4,0).
关于x轴的对称点A′(____,____)B′(_____,______)C′(_____,_____)D′(____,_____)E′(_____,_____).
关于y轴的对称点A″(_____,____)B″(_____,______)C″(_____,_____)D″(____,_____)E″(_____,_____).
设计意图:
通过学生动手操作,分别作A,B,C,D,E关于x轴、y轴的对称点A′,B′,C′,D′,E′;A″,B″,C″,D″,E″,并且求出它们的坐标,观察,归纳它们坐标之间的关系.
师生行为:
教师引导,学生自主探索发现关于x轴、y轴对称的每组对称点坐标的规律.
[生]如图,我们先在直角坐标系中描出A(2,-3),B(-1,2),C(-6,-5),D(,1),E(4,0)点.
我们先在坐标系中作出A点关于x轴的对称点,即过A作x轴的垂线交x轴于M点,M点的坐标为(2,0).在AM的延长线上截A′M=AM,则A′就是A点关于x轴的对称点,所以A′在第一象限,因为A′M=AM,所以A′的纵坐标为3,因为AA′⊥x轴,即AA′∥y轴,所以A′的横坐标为2,即A′的坐标为(2,3).
同理可求得B,C,D,E关于x轴的对称点B′,C′,D′,E′的坐标分别为B′(-1,-2),C′(-6,5),D′(,-1),E′(4,0).列表如下:
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
关于x轴的对称点
A′(2,3)
B′(-1,-2)
C′(-6,5)
续表
已知点
D(,1)
E(4,0)
关于x轴的对称点
D′(,-1)
E′(4,0)
[师]观察上表每对对称点坐标之间的关系,你发现什么规律?
[生]每对对称点的横坐标相同,纵坐标互为相反数.
[师]我们不仿再找几对关于x轴对称的点,写出它们的坐标,还有上面的规律吗?
学生亲自动手进一步尝试,在学生认可的情况下明确关于x轴对称的每对对称点的坐标的规律.
[师生共析]
关于x轴对称的每对对称点的坐标:横坐标相同,纵坐标互为相反数.
接着我们再来作出A,B,C,D,E关于y轴的对称点,并求出它们的坐标.
[生]同样,我们先作出A关于y轴的对称点A″,并求出A″的坐标.
过A作y轴的垂线AN,垂足为N,则N点坐标为(0,-3),然后在AN的延长线上截A″N,使A″N=AN,则A″就是所求的A关于y轴的对称点.A″在第三象限,AA″⊥y轴,且AN=A″N,所以A″的坐标为(-2,-3),同理可求得B,C,D,E关于y轴的对称点B″,C″,D″,E″的坐标分别为B″(1,2),C″(6,-5),D″(-,1),E″(-4,0).列表如下:
已知点
A(2,-3)
B(-1,2)
C(-6,-5)
关于y轴对称点
A″(-2,-3)
B″(1,2)
C″(6,-5)
续表
已知点
D(,1)
E(4,0)
关于y轴对称点
D″(,1)
E″(-4,0)
[师]观察上表,比较每对关于y轴的对称点的坐标,你能发现什么规律?
[生]关于y轴对称的每一对对称点的坐标纵坐标相同,横坐标互为相反数.
Ⅲ.随堂练习
[活动3]
练习:(教科书P41练习)
1.分别写出下列各点关于x轴和y轴对称的点的坐标:
(-2,6),(1,-2),(-1,3),(-4,-2),(1,0).
2.如图,△ABC关于x轴对称,点A的坐标为(1,-2),标出点B的坐标.
3.如图,利用关于坐标轴对称的点的坐标的特点,分别作出与△ABC关于x轴和y轴对称的图形.
设计意图:
巩固关于x轴、y轴对称的每对对称点的坐标规律.根据已知点,能求出关于x轴、y轴对称的点的坐标,并能利用关于坐标轴对称的点的坐标特点,作出与已知图形关于坐标轴对称的图形.
师生行为:
学生练习,教师巡视,师生共评.
[生]1.解:根据关于x轴对称的点的坐标的特点求得(-2,6),(1,-2),(-1,3),(-4,-2),(1,0)关于x轴对称的点的坐标分别为(-2,-6),(1,2),(-1,-3),(-4,2),(1,0).
根据关于y轴对称的点的坐标的特点可得(-2,6),(1,-2),(-1,3),(-4,-2),(1,0)关于y轴对称的点的坐标分别为(2,6),(-1,-2),(1,3),(4,-2),(-1,0).
2.△ABC关于x轴对称,则A、B为关于x轴的一对对称点,已知A的坐标为(1,-2),则B的坐标为(1,2).
3.分析:要作出与△ABC关于x轴、y轴的对称图形,只需把A、B、C关于x轴、y轴的对称点找到即可.
解:△ABC各顶点的坐标:A(-4,1),B(-1,-1),C(-3,2)它们关于x轴对称的点的坐标为A1(-4,-1),B1(-1,1),C1(-3,-2).在同一直角坐标系中描出A1(-4,-1),B1(-1,1),C1(-3,-2)连结A1B1,B1C1,C1A1,则△A1B1C1就是△ABC关于x轴对称的图形(如图).
A(-4,1),B(-1,-1),C(-3,2)它们关于y轴对称的点的坐标为A2(4,1),B2(1,-1),C2(3,2).在同一坐标系中描出A2(4,1),B2(1,-1),C2(3,2),连结A2B2,B2C2,C2A2,则△A2B2C2就是△ABC关于y轴对称的图形(如图).
[活动4]
补充练习:
1.将下图中的点(2,1),(5,1),(2,5)做如下变化:
(1)纵坐标不变,横坐标分别加2.
(2)横坐标不变,纵坐标分别加1.
(3)纵坐标不变,横坐标分别变为原来的2倍.
(4)横坐标不变,纵坐标分别变为原来的2倍.
(5)纵坐标不变,横坐标分别乘以-1.
(6)横坐标不变,纵坐标分别乘以-1.
(7)纵坐标、横都分别乘以-1,观察变化后的三角形与原三角形有什么变化?
设计意图:
进一步让同学们亲身经历点的坐标的变化与图形变换之间的关系.
师生行为:
学生练习,教师指导.
精析:行根据变化,把每次变化后的三个顶点坐标求出,在平面直角坐标系中描出它们,连结成新三角形,然后与原有的三角形进行比较.
精解:(1)纵坐标不变,横坐标分别加2得三个点依次为(4,1),(7,1),(4,5).将各点用线段依次连结起来,所得图形如图(1)所示,与原图形相比三角形的形状、大小不变,整个三角形向右平移了2个单位长度.
(2)横坐标不变,纵坐标分别加1,得三个点依次为(2,2),(5,2),(2,6).将各点用线段依次连结起来,所得图形如图(2)所示,与原图形相比,三角形的形状、大小不变,整个三角形向上平移了1个单位长度.
(3)纵坐标不变,横坐标分别变为原来的2倍,得三个点依次为(4,1),(10,1),(4,5).将各点用线段依次连结起来,所得图形如图(3)所示,与原图形相比,整个三角形被横向拉长为原来的2倍.
(4)横坐标不变,纵坐标分别变为原来的2倍,得三个点依次为(2,2),(5,2),(2,10).将各点依次用线段连结起来,所得图形如图(4)所示,与原图形相比,整个三角形被纵向拉长2倍.
(5)纵坐标不变,横坐标分别乘以-1,得三个点坐标为(-2,1),(-5,1),(-2,5).将各点依次用线段连结起来,如图(5)所示,与原图形相比,三角形的形状、大小不变,整个三角形与原三角形关于y轴对称.
(6)横坐标不变,纵坐标分别乘以-1,得三个点坐标为(2,-1),(5,-1),(2,-5).将各点用线段连结起来,如图(6)所示,与原图形相比,三角形的形状、大小不变,整个三角形与原三角形关于x轴对称.
(7)横纵坐标都分别乘以-1,得三个点坐标为(-2,-1),(-5,-1),(-2,-5).将各点用线段依次连结起来,如图(7)所示,与原图形相比,整个三角形的形状、大小不变,整个三角形与原三角形关于O点对称.
Ⅳ.课时小结
本节课的主要内容(由学生在教师的引导下共同回忆总结):
1.在直角坐标系中,探索了关于x轴,y轴对称的对称点坐标规律.
2.利用关于坐标轴对称的点的坐标的特点,作已知图形的轴对称图形,体现了数形结合的数学思想.
Ⅴ.课后作业
教科书习题12.2─2、3、4题,第6题、第7题(学有余力的同学做).
Ⅵ.活动与探究
如下图,以树干为对称轴,画出树的另一半.
分析:要画出树的另一半,根据轴对称图形的性质,关于对称轴对称的对应点的横坐标是互为相反数,纵坐标不变,因此需要在图中先建立直角坐标系,写出对称轴左侧某些点的坐标,然后对称地写出右侧的对应点的坐标,再进行连结.
解:如上图所示建立直角坐标系,对称轴为y轴,y轴左侧的点A、C两点的坐标为(-4,0)、(-3,4),对称点A′、C′的坐标为(4,0)、(3,4),O、B、D三点都在对称轴上,然后用线段连结起来.
2.A、B、C、D、E各点的坐标如下图所示,确定△ABE、△EBD、△ABC的面积,你是怎样做的?你发现了什么规律?
解:A、B、C、D、E各点的坐标分别为A(0,6),B(0,3),C(6,1),D(-2,-2),E(-8,0).
△ABE的面积为(8×6-8×3)=12.
△EBD的面积为8×5- ×8×3- ×2×5- ×6×2=17.
△ABC的面积为(6×5-2×6)=9.
规律为可以将每个三角形的面积看成边与坐标轴平行的矩形的一半.
板书设计
§12.2.2 用坐标表示轴对称
一、探索关于x轴、y轴对称的每对对称点的规律.
(1)关于x轴对称的点的坐标横坐标相同,纵坐标互为相反数.
(2)关于y轴对称的点的坐标纵坐标相同,横坐标互为相反数.
二、利用关于x轴、y轴对称的点的坐标的规律,能作出关于x轴、y轴对称的图形.
备课资料
(一)参考练习
1.已知A点坐标为(-1,3).
(1)与点A关于y轴对称的点坐标.
(2)与点A关于x轴对称的点坐标.
2.已知△ABC的顶点坐标分别为(3,3),(2,1),(4,1).请你在同一坐标系中作出:
(1)关于x轴对称的图形.
(2)关于y轴对称的图形.
3.描出图中的枫叶图案关于x轴的轴对称图形的简图.
