人教版小学六年级数学下3.2.2 圆锥的体积课件
文档属性
| 名称 | 人教版小学六年级数学下3.2.2 圆锥的体积课件 |  | |
| 格式 | zip | ||
| 文件大小 | 2.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-01-30 17:55:43 | ||
图片预览




文档简介
课件26张PPT。第3单元 圆柱与圆锥
2.圆锥
第5节 圆锥的体积
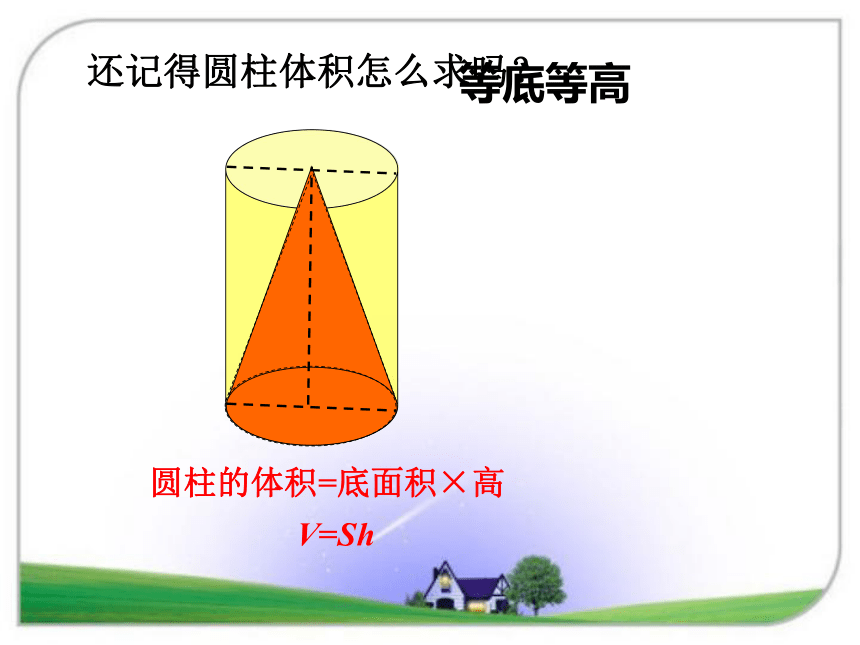
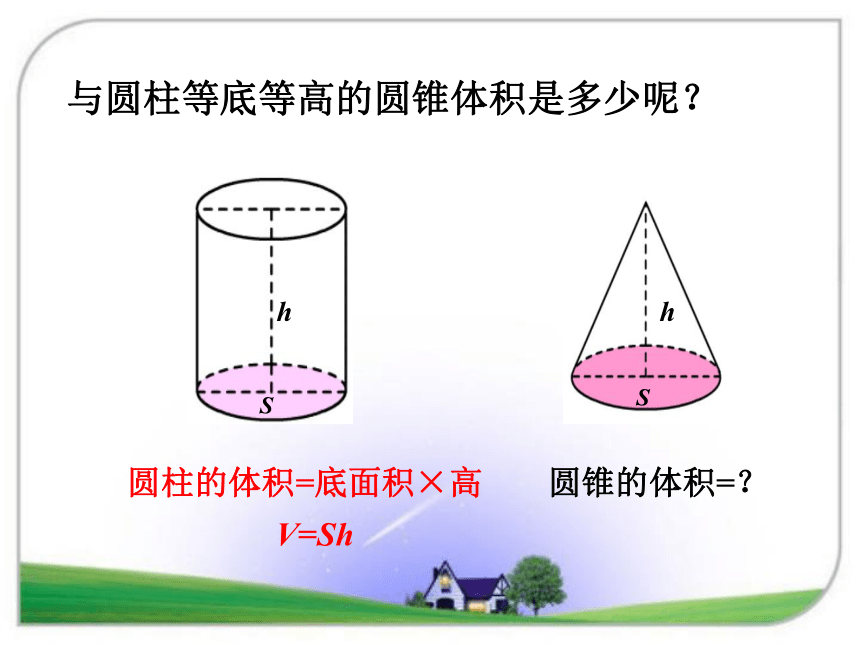
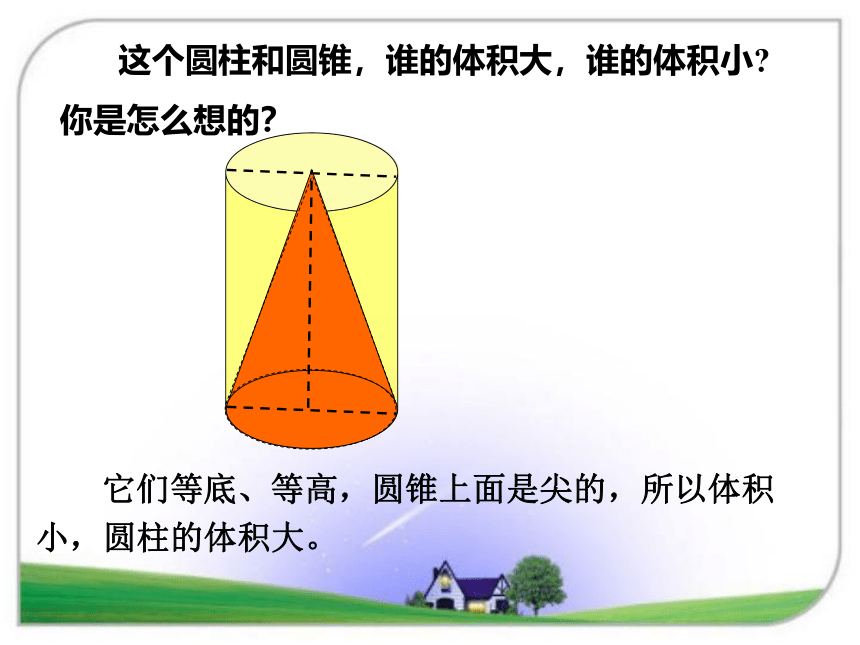
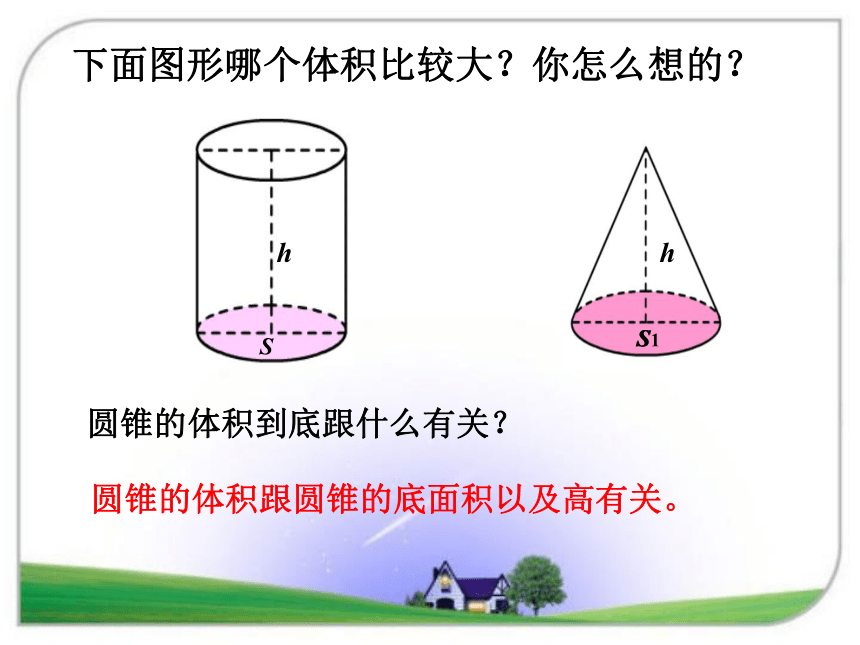
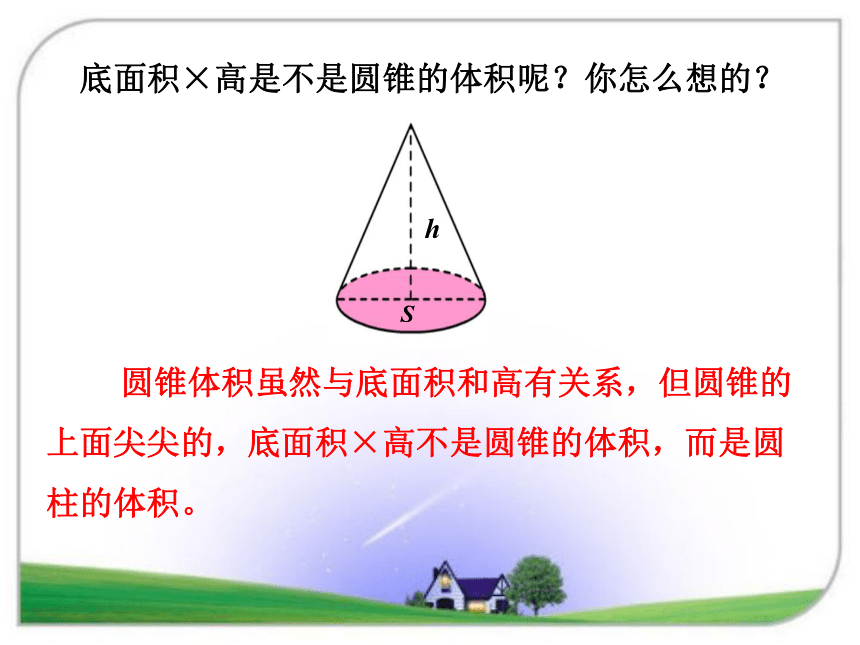
看到这些图片,你有什么感受?一、设疑引起学生兴趣,引出课题等底等高圆柱的体积=底面积×高V=Sh还记得圆柱体积怎么求吗?与圆柱等底等高的圆锥体积是多少呢?ShSh圆柱的体积=底面积×高V=Sh圆锥的体积=? 这个圆柱和圆锥,谁的体积大,谁的体积小?你是怎么想的? 它们等底、等高,圆锥上面是尖的,所以体积小,圆柱的体积大。下面图形哪个体积比较大?你怎么想的?ShShSh1下面图形哪个体积比较大?你怎么想的?ShShS1圆锥的体积到底跟什么有关? 圆锥的体积跟圆锥的底面积以及高有关。底面积×高是不是圆锥的体积呢?你怎么想的? 圆锥体积虽然与底面积和高有关系,但圆锥的上面尖尖的,底面积×高不是圆锥的体积,而是圆柱的体积。 以长方形的一条边为轴旋转一周,会形成什么形状?闭眼想象一下。 圆柱如果把长方形沿对角线平均分成两个完全一样的直角三角形,以它的一条直角边为轴旋转一周,会形成什么形状?闭眼想象一下。 圆锥三角形面积是长方形面积的二分之一,那么圆锥是圆柱体积的几分之几呢??科学不能靠想象,而是要靠科学的试验来验证。这个圆柱和圆锥有什么特点呢?等底、等高方法一:实验
方法二:计算
方法三:……二、科学验证,研究问题 到底是几分之几呢?你们有什么好办法来验证一下吗?方法一:实验方法二:计算 实心的圆锥和圆柱,将能沉入水中的圆柱和圆锥沉入容器水中,分别记录水位高度,或将与圆柱等底、等高的圆锥放入装满水的圆柱里,水会溢出来,水的体积就是圆锥的体积。方法三:借助其他工具,验证公式。 把等底、等高的圆柱和圆锥两种容器都装满大米,然后在天平上分别称出所装大米的质量,两种容器容纳的大米质量恰好成3倍关系。根据:同密度物体的体积与质量成正比研究结论 圆柱的体积是与它等底、等高的圆锥体积的3倍,或圆锥体积是与它等底、等高的圆柱体积的 。工地上有一堆沙子,近似于一个圆锥。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨?三、运用所学知识,解决问题 1.填空。
(1)一个圆柱的体积是75.36 m3,与它等底、等高的圆锥的体积是( ) m3 。
(2)一个圆锥的体积是141.3 cm3 ,与它等底、等高的圆柱的体积是( ) cm3 。25.12423.9四、巩固练习 2.动脑筋想一想,要使等底、等高的圆柱和圆锥的体积相等,你有什么办法吗? 老师这里有一个圆柱和圆锥,它们是等底、等高的,这时圆锥体积是圆柱体积的 ,圆柱体积是圆锥体积的3倍,如果要想使它们的体积相等,该怎么办? 把圆锥的高或底面积扩大到原来的3倍,使圆锥的体积扩大到原来的3倍,与圆柱的体积相等。 老师这里有一个圆柱和圆锥,它们是等底、等高的,这时圆锥体积是圆柱体积的 ,圆柱体积是圆锥体积的3倍,如果要想使它们的体积相等,该怎么办? 3.一个圆锥形的零件,底面积是19 cm2,高是12 cm,这个零件的体积是多少? 4.一个用钢铸造成的圆锥形铅锤,底面直径是4 cm,高5 cm。每立方厘米钢大约重7.8 g。这个铅锤重多少克?(得数保留整数。)通过这节课的学习,你有哪些收获?五、课堂小结谢谢大家!
再见!
2.圆锥
第5节 圆锥的体积
看到这些图片,你有什么感受?一、设疑引起学生兴趣,引出课题等底等高圆柱的体积=底面积×高V=Sh还记得圆柱体积怎么求吗?与圆柱等底等高的圆锥体积是多少呢?ShSh圆柱的体积=底面积×高V=Sh圆锥的体积=? 这个圆柱和圆锥,谁的体积大,谁的体积小?你是怎么想的? 它们等底、等高,圆锥上面是尖的,所以体积小,圆柱的体积大。下面图形哪个体积比较大?你怎么想的?ShShSh1下面图形哪个体积比较大?你怎么想的?ShShS1圆锥的体积到底跟什么有关? 圆锥的体积跟圆锥的底面积以及高有关。底面积×高是不是圆锥的体积呢?你怎么想的? 圆锥体积虽然与底面积和高有关系,但圆锥的上面尖尖的,底面积×高不是圆锥的体积,而是圆柱的体积。 以长方形的一条边为轴旋转一周,会形成什么形状?闭眼想象一下。 圆柱如果把长方形沿对角线平均分成两个完全一样的直角三角形,以它的一条直角边为轴旋转一周,会形成什么形状?闭眼想象一下。 圆锥三角形面积是长方形面积的二分之一,那么圆锥是圆柱体积的几分之几呢??科学不能靠想象,而是要靠科学的试验来验证。这个圆柱和圆锥有什么特点呢?等底、等高方法一:实验
方法二:计算
方法三:……二、科学验证,研究问题 到底是几分之几呢?你们有什么好办法来验证一下吗?方法一:实验方法二:计算 实心的圆锥和圆柱,将能沉入水中的圆柱和圆锥沉入容器水中,分别记录水位高度,或将与圆柱等底、等高的圆锥放入装满水的圆柱里,水会溢出来,水的体积就是圆锥的体积。方法三:借助其他工具,验证公式。 把等底、等高的圆柱和圆锥两种容器都装满大米,然后在天平上分别称出所装大米的质量,两种容器容纳的大米质量恰好成3倍关系。根据:同密度物体的体积与质量成正比研究结论 圆柱的体积是与它等底、等高的圆锥体积的3倍,或圆锥体积是与它等底、等高的圆柱体积的 。工地上有一堆沙子,近似于一个圆锥。这堆沙子的体积大约是多少?如果每立方米沙子重1.5 t,这堆沙子大约重多少吨?三、运用所学知识,解决问题 1.填空。
(1)一个圆柱的体积是75.36 m3,与它等底、等高的圆锥的体积是( ) m3 。
(2)一个圆锥的体积是141.3 cm3 ,与它等底、等高的圆柱的体积是( ) cm3 。25.12423.9四、巩固练习 2.动脑筋想一想,要使等底、等高的圆柱和圆锥的体积相等,你有什么办法吗? 老师这里有一个圆柱和圆锥,它们是等底、等高的,这时圆锥体积是圆柱体积的 ,圆柱体积是圆锥体积的3倍,如果要想使它们的体积相等,该怎么办? 把圆锥的高或底面积扩大到原来的3倍,使圆锥的体积扩大到原来的3倍,与圆柱的体积相等。 老师这里有一个圆柱和圆锥,它们是等底、等高的,这时圆锥体积是圆柱体积的 ,圆柱体积是圆锥体积的3倍,如果要想使它们的体积相等,该怎么办? 3.一个圆锥形的零件,底面积是19 cm2,高是12 cm,这个零件的体积是多少? 4.一个用钢铸造成的圆锥形铅锤,底面直径是4 cm,高5 cm。每立方厘米钢大约重7.8 g。这个铅锤重多少克?(得数保留整数。)通过这节课的学习,你有哪些收获?五、课堂小结谢谢大家!
再见!
