(沪教版)五年级数学下册 列方程解应用题 行程与工程问题专题 课件
文档属性
| 名称 | (沪教版)五年级数学下册 列方程解应用题 行程与工程问题专题 课件 |  | |
| 格式 | zip | ||
| 文件大小 | 1.0MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-01 20:01:54 | ||
图片预览






文档简介
课件18张PPT。列方程解应用题(2)
行程问题沪教版五年级数学下册行程问题的几个公式路程=速度×时间
s=v×t
速度=路程÷时间
v=s÷t
时间=路程÷速度
t=s÷v探究一:相遇问题 2.两辆车同时从相距441千米的甲、乙两地相向而行,客车每小时行78千米,货车每小时行48千米,多少小时后两车相遇?
解:x小时后两车相遇
78x+48x=441
126x=441
X=3.5
答:3.5小时后两车相遇。相向:相对的方向
分析:两车相对行驶,只要有交点,就算相遇,那么两车相加的路程就是甲、乙两地相距的路程。练习一:1.一列快车从天津开出,平均每小时行79千米;同时有一列慢车从济南开出,平均每小时行40千米。经过3小时两车相遇,天津到济南的铁路长多少米?解:设天津到济南的铁路长x千米
X=79×3+40×3
X=237+120
X=357
357千米=327000米
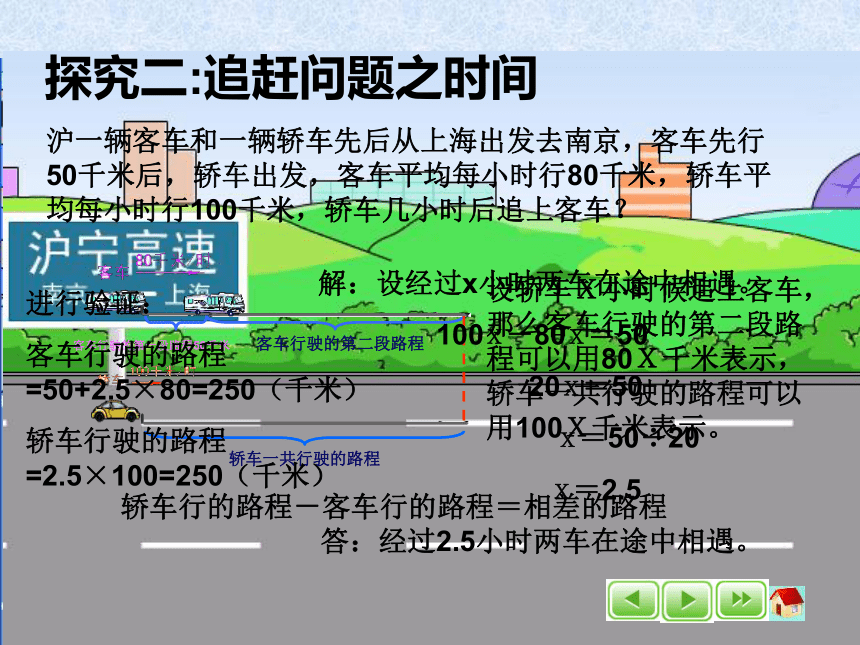
答:天津到济南的铁路长327000米。注意单位探究二:追赶问题之时间沪一辆客车和一辆轿车先后从上海出发去南京,客车先行50千米后,轿车出发,客车平均每小时行80千米,轿车平均每小时行100千米,轿车几小时后追上客车?客车行驶的第一段路程50千米客车行驶的第二段路程轿车一共行驶的路程设轿车X小时候追上客车,那么客车行驶的第二段路程可以用80X千米表示,轿车一共行驶的路程可以用100X千米表示。轿车行的路程-客车行的路程=相差的路程 解:设经过x小时两车在途中相遇。
100X-80X=50
20X=50
X=50÷20
X=2.5
答:经过2.5小时两车在途中相遇。 进行验证:
客车行驶的路程=50+2.5×80=250(千米)
轿车行驶的路程=2.5×100=250(千米) 练习二:1、小胖上学时忘了带文具盒,爸爸发现时,小胖刚好离家512米,正以72米/分的速度走向学校,爸爸骑车以200米/分的速度追赶,爸爸几分钟后在途中追上小胖? 解:设爸爸x分钟后在途中追上小胖
72x+512=200x
200x-72x=512
128x=512
X=4
答:爸爸4分钟后在途中追上小胖。
练习二:2、甲、乙两人赛跑,甲的速度是7米/秒,乙的速度是5.5米/秒,甲在乙后面21米,两人同时同向跑步,问甲经过几秒钟追上乙?解:设甲经过x秒追上乙
5.5x+21=7x
7x-5.5x=21
1.5x=21
X=14
答:甲经过14秒追上乙。
探究三:追赶问题之路程张兴和李忠两人分别从A、B两地同时由西向东而行,张兴骑摩托车从A地出发,速度是45千米/时,李忠骑自行车从B地出发,速度是15千米/时,2小时后张兴追上了李忠。求A、B两地的距离。AB张李45千米/时15千米/时2小时2小时?解:设A、B两地相距x千米。
15×2+x=45×2
30+x=90
x=60
答: A、B两地相距60千米。李忠行的路程+ A、B两地距离=张兴行的路程练习三:体育课上,小胖站在跑道的起点处,小亚站在他前面某处,两人同时同向起跑,30秒后小胖追上小亚。已知小亚平均每秒跑3米,小胖平均每秒跑5米,问小亚离起点多少米开始跑步?解:设小亚离起点x米开始跑步
x+3×30=5×30
x =150-90
x =60
答:小亚离起点60米开始起跑。
探究四:追赶问题之速度
小丁和小巧跑步锻炼身体,小巧跑出200米后小丁从起点出发,小丁平均每分钟跑170米,5分钟后在途中追上小巧,小巧平均每分钟跑多少米? 解:设小巧平均每分钟跑x米
200+5x=170×5
5x=850-200
5x=650
X=130
答:小巧平均每分钟跑130米。分析:
小巧:先跑出200米,然后从200米处走了5分钟。
小丁:从原点出发,走了5分钟
两人走的路程却是相同的。
练习四:1.一艘快艇从甲港经乙港开往丙,每小时行38千米,同时一艘轮船从乙港开往丙港,4小时后两船同时达到丙港。已知甲乙两港相距24千米,求轮船的速度。解:设轮船的速度为x
4×38-24=4x
4x=128
X=32
答:轮船的速度为32千米/小时。本课小结相遇问题:抓住相遇的交点,看看哪一个量是相遇两物体共有的,以此为基准找出相应的等量关系。
追赶问题:两物体在同一段路程中同向而行,尽管速度较慢的物体先行,但在一定的时间中,速度较快的车一定能追上速度较慢的物体。用多少时间能追上,我们可以根据题意找出相应的等量关系式。列方程解应用题(2)
工程问题沪教版五年级数学下册工程问题的几个公式工程量=速度×时间
速度=工程量÷时间
时间=工程量÷速度探究一:1.王师傅和他的徒弟零件加工厂工作,由于王师傅工作经验丰富,所以他能够一小时加工30个零件,徒弟一小时加工的个数是王师傅的一半,徒弟先做2小时,再由两人合作,能够完成一天165个的指标,请问两人合作的时间是多少。解:设两人合作的时间为x小时
15×2+30x+15x=165
30+45x=165
X=3
答:两人合作的时间为3小时。分析:
徒弟先做的工程,与师徒两人合作的工程加起来就是一天的指标,即总工程量。练习一:1.甲、乙两个工程队合作修建一条长45千米的铁路,甲修建的速度是5千米/小时,现接到通知,要求两队3小时内修建完毕,请问乙一小时至少要修多少米才能按时完成任务。解:设乙一小时至少要修x米才能按时完成任务
5×3+3x=45
2x=45-15
2x=30
X=15
答:乙一小时至少要修15米才能按时完成任务。复习:解答应用题的基本步骤:(1)审题——弄清题意,找出未知数,
并用x表示;
(3)计算——解方程;(4)检验——写出答案。(2)分析——找出应用题中数量之间的相等关系,列方程;列方程解应用题的思考方法读题-------理解每一句话的意义。设 -------设未知数为x。★划-------划出表示两个量关系的句子。★想-------根据关键句写出等量关系式。找 -------根据等量关系找出已知量和未知量的两个相关的条件。写 -------根据两个相关的条件写出小式子。列 --------列出方程求解。
行程问题沪教版五年级数学下册行程问题的几个公式路程=速度×时间
s=v×t
速度=路程÷时间
v=s÷t
时间=路程÷速度
t=s÷v探究一:相遇问题 2.两辆车同时从相距441千米的甲、乙两地相向而行,客车每小时行78千米,货车每小时行48千米,多少小时后两车相遇?
解:x小时后两车相遇
78x+48x=441
126x=441
X=3.5
答:3.5小时后两车相遇。相向:相对的方向
分析:两车相对行驶,只要有交点,就算相遇,那么两车相加的路程就是甲、乙两地相距的路程。练习一:1.一列快车从天津开出,平均每小时行79千米;同时有一列慢车从济南开出,平均每小时行40千米。经过3小时两车相遇,天津到济南的铁路长多少米?解:设天津到济南的铁路长x千米
X=79×3+40×3
X=237+120
X=357
357千米=327000米
答:天津到济南的铁路长327000米。注意单位探究二:追赶问题之时间沪一辆客车和一辆轿车先后从上海出发去南京,客车先行50千米后,轿车出发,客车平均每小时行80千米,轿车平均每小时行100千米,轿车几小时后追上客车?客车行驶的第一段路程50千米客车行驶的第二段路程轿车一共行驶的路程设轿车X小时候追上客车,那么客车行驶的第二段路程可以用80X千米表示,轿车一共行驶的路程可以用100X千米表示。轿车行的路程-客车行的路程=相差的路程 解:设经过x小时两车在途中相遇。
100X-80X=50
20X=50
X=50÷20
X=2.5
答:经过2.5小时两车在途中相遇。 进行验证:
客车行驶的路程=50+2.5×80=250(千米)
轿车行驶的路程=2.5×100=250(千米) 练习二:1、小胖上学时忘了带文具盒,爸爸发现时,小胖刚好离家512米,正以72米/分的速度走向学校,爸爸骑车以200米/分的速度追赶,爸爸几分钟后在途中追上小胖? 解:设爸爸x分钟后在途中追上小胖
72x+512=200x
200x-72x=512
128x=512
X=4
答:爸爸4分钟后在途中追上小胖。
练习二:2、甲、乙两人赛跑,甲的速度是7米/秒,乙的速度是5.5米/秒,甲在乙后面21米,两人同时同向跑步,问甲经过几秒钟追上乙?解:设甲经过x秒追上乙
5.5x+21=7x
7x-5.5x=21
1.5x=21
X=14
答:甲经过14秒追上乙。
探究三:追赶问题之路程张兴和李忠两人分别从A、B两地同时由西向东而行,张兴骑摩托车从A地出发,速度是45千米/时,李忠骑自行车从B地出发,速度是15千米/时,2小时后张兴追上了李忠。求A、B两地的距离。AB张李45千米/时15千米/时2小时2小时?解:设A、B两地相距x千米。
15×2+x=45×2
30+x=90
x=60
答: A、B两地相距60千米。李忠行的路程+ A、B两地距离=张兴行的路程练习三:体育课上,小胖站在跑道的起点处,小亚站在他前面某处,两人同时同向起跑,30秒后小胖追上小亚。已知小亚平均每秒跑3米,小胖平均每秒跑5米,问小亚离起点多少米开始跑步?解:设小亚离起点x米开始跑步
x+3×30=5×30
x =150-90
x =60
答:小亚离起点60米开始起跑。
探究四:追赶问题之速度
小丁和小巧跑步锻炼身体,小巧跑出200米后小丁从起点出发,小丁平均每分钟跑170米,5分钟后在途中追上小巧,小巧平均每分钟跑多少米? 解:设小巧平均每分钟跑x米
200+5x=170×5
5x=850-200
5x=650
X=130
答:小巧平均每分钟跑130米。分析:
小巧:先跑出200米,然后从200米处走了5分钟。
小丁:从原点出发,走了5分钟
两人走的路程却是相同的。
练习四:1.一艘快艇从甲港经乙港开往丙,每小时行38千米,同时一艘轮船从乙港开往丙港,4小时后两船同时达到丙港。已知甲乙两港相距24千米,求轮船的速度。解:设轮船的速度为x
4×38-24=4x
4x=128
X=32
答:轮船的速度为32千米/小时。本课小结相遇问题:抓住相遇的交点,看看哪一个量是相遇两物体共有的,以此为基准找出相应的等量关系。
追赶问题:两物体在同一段路程中同向而行,尽管速度较慢的物体先行,但在一定的时间中,速度较快的车一定能追上速度较慢的物体。用多少时间能追上,我们可以根据题意找出相应的等量关系式。列方程解应用题(2)
工程问题沪教版五年级数学下册工程问题的几个公式工程量=速度×时间
速度=工程量÷时间
时间=工程量÷速度探究一:1.王师傅和他的徒弟零件加工厂工作,由于王师傅工作经验丰富,所以他能够一小时加工30个零件,徒弟一小时加工的个数是王师傅的一半,徒弟先做2小时,再由两人合作,能够完成一天165个的指标,请问两人合作的时间是多少。解:设两人合作的时间为x小时
15×2+30x+15x=165
30+45x=165
X=3
答:两人合作的时间为3小时。分析:
徒弟先做的工程,与师徒两人合作的工程加起来就是一天的指标,即总工程量。练习一:1.甲、乙两个工程队合作修建一条长45千米的铁路,甲修建的速度是5千米/小时,现接到通知,要求两队3小时内修建完毕,请问乙一小时至少要修多少米才能按时完成任务。解:设乙一小时至少要修x米才能按时完成任务
5×3+3x=45
2x=45-15
2x=30
X=15
答:乙一小时至少要修15米才能按时完成任务。复习:解答应用题的基本步骤:(1)审题——弄清题意,找出未知数,
并用x表示;
(3)计算——解方程;(4)检验——写出答案。(2)分析——找出应用题中数量之间的相等关系,列方程;列方程解应用题的思考方法读题-------理解每一句话的意义。设 -------设未知数为x。★划-------划出表示两个量关系的句子。★想-------根据关键句写出等量关系式。找 -------根据等量关系找出已知量和未知量的两个相关的条件。写 -------根据两个相关的条件写出小式子。列 --------列出方程求解。
