5.4 平移同步练习
图片预览



文档简介
5.4平移同步练习
姓名________________考号_________总分____________
本节应掌握和应用的知识
平移:把一个图形整体沿某一直线方向移动 ,叫平移.
2. 平移的性质
(1)新图形与原图形形状、大小完全相同;
(2)新图形上的每一点都是由它的对应点平移后得到的;
(3)连接各组对应点的线段平行(或在同一条直线上)且相等 .
基础知识和能力拓展训练
一、选择题
1.下列现象中是平移的是( )
A. 将一张纸沿它的中线折叠????? B. 飞碟的快速转动?????
C. 电梯的上下移动????? D. 翻开书中的每一页纸张
2.下列选项中能由左图平移得到的是( )
A. B. C. D.
3.在以下现象中:①在笔直的公路上行驶的汽车;②用打气筒给自行车打气时,气筒里活塞的运动;③随风摆动的旗帜;④小河里流动的水流.属于平移的是( )
A.① B.①② C.①②③ D.①②③④
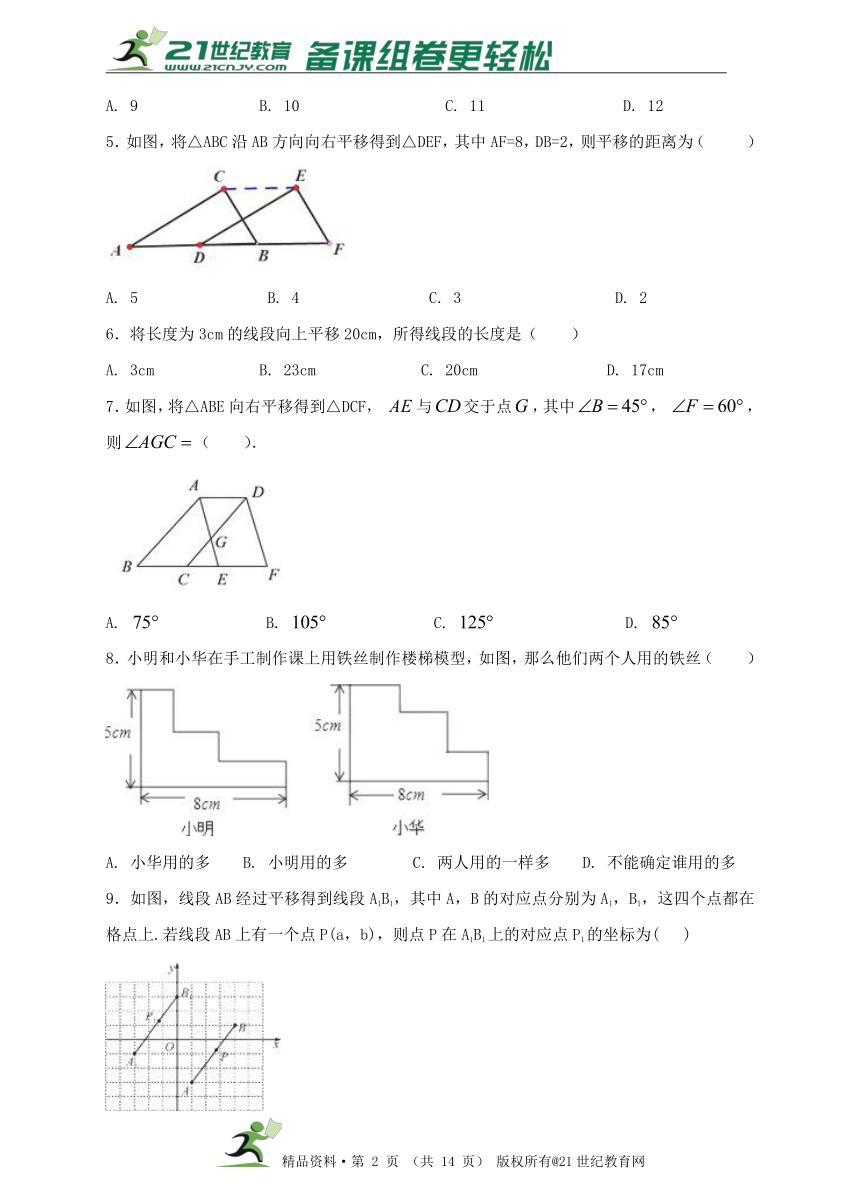
4.如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )www.21-cn-jy.com
A. 9 B. 10 C. 11 D. 12
5.如图,将△ABC沿AB方向向右平移得到△DEF,其中AF=8,DB=2,则平移的距离为( )
A. 5 B. 4 C. 3 D. 2
6.将长度为3cm的线段向上平移20cm,所得线段的长度是( )
A. 3cm B. 23cm C. 20cm D. 17cm
7.如图,将△ABE向右平移得到△DCF, 与交于点,其中, ,则( ).
A. B. C. D.
8.小明和小华在手工制作课上用铁丝制作楼梯模型,如图,那么他们两个人用的铁丝( )
A. 小华用的多 B. 小明用的多 C. 两人用的一样多 D. 不能确定谁用的多
9.如图,线段AB经过平移得到线段A1B1,其中A,B的对应点分别为A1,B1,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
A. (a-4,b+2) B. (a-4,b-2) C. (a+4,b+2) D. (a+4,b-2)
二、填空题
10.在如图所示的草坪上,铺设一条宽为2的小路,则小路的面积___________.
11.如图,将△ABC平移到△A′B′C′的位置(点B′在AC边上),若∠B=55°,∠C=100°,则∠AB′A′的度数为________________°21教育名师原创作品
12.如图,将线段AB沿箭头方向平移2 cm得到线段CD,若AB=3 cm,则四边形ABDC的周长为___cm.
13.如图所示,由三角形ABC平移得到的三角形有_______个.
14.如图,边长为4cm 的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形,此时阴影部分的面积为_______________cm2.
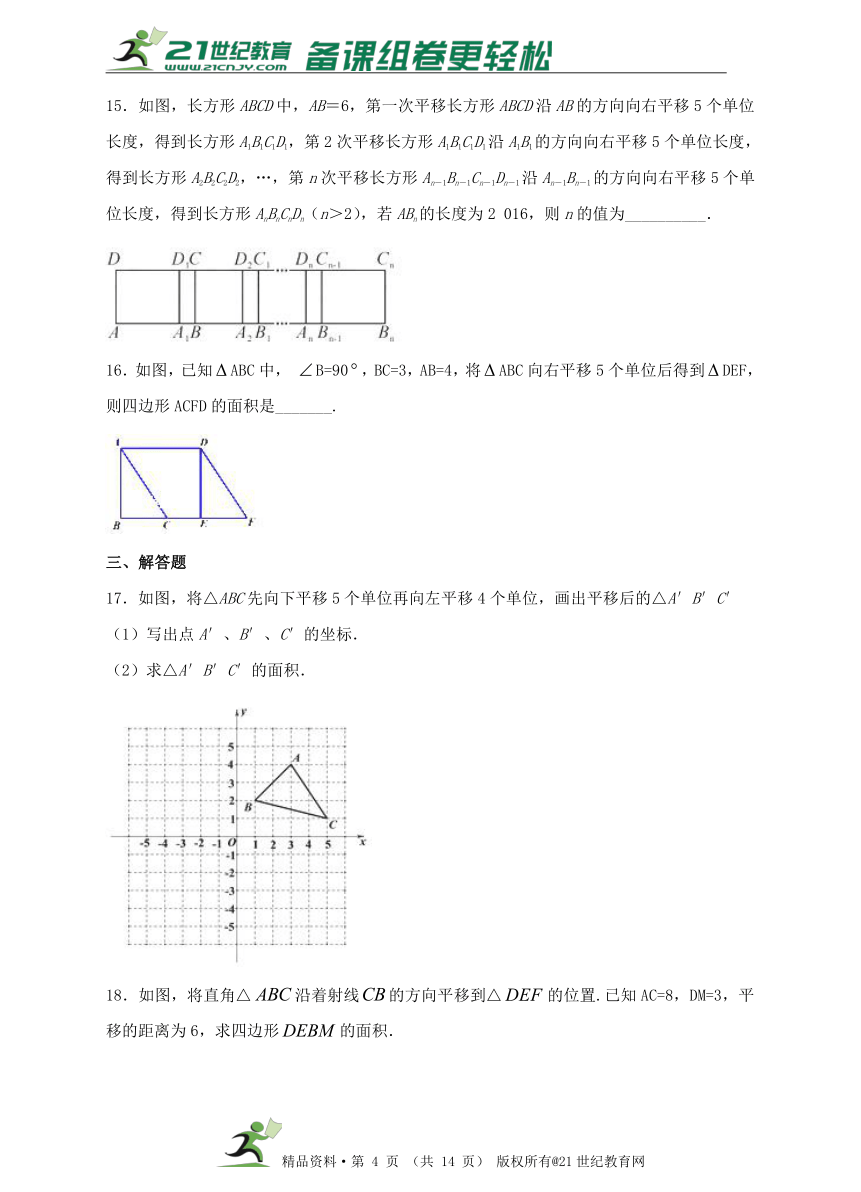
15.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2 016,则n的值为__________.
16.如图,已知ABC中, B=90,BC=3,AB=4,将ABC向右平移5个单位后得到DEF,则四边形ACFD的面积是_______.
三、解答题
17.如图,将△ABC先向下平移5个单位再向左平移4个单位,画出平移后的△A′B′C′
(1)写出点A′、B′、C′的坐标.
(2)求△A′B′C′的面积.
18.如图,将直角△沿着射线的方向平移到△的位置.已知AC=8,DM=3,平移的距离为6,求四边形的面积. 21教育网
19.(1)如图所示,小明准备在C处牵牛到河边AB饮水,按下列要求作图并说明理由.
①请用三角板作出小明的最短路线(不考虑其他因素);
②如图乙,若小明在C处牵牛到河边AB饮水,并且必须到河边D处观察河水的水质情况,请作出小明行走的最短路线。
(2)经过平移,图中左边图形上A点移到E点,作出平移后的图形。
理由: ;理由: 。
20.如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)
21. 白云宾馆在装修时,准备在主楼梯上铺上红地毯,已知这种地毯每平方米售价30元,主楼梯宽2m,其侧面如图所示,则购买这种地毯至少需要多少元?21*cnjy*com
参考答案
1.C
【解析】A. 将一张纸沿它的中线折叠,不符合平移定义,故本选项错误;
B. 飞蝶的快速转动,不符合平移定义,故本选项错误;
C. 电梯的上下移动,符合平移的定义,正确;
D. 翻开书中的每一页纸张,不符合平移的定义,故本选项错误。
故选C.
2.C
【解析】试题解析:能由左图平移得到的是:选项C. 故选C.
3.B
【解析】①在笔直的公路上行驶的汽车沿直线运动,符合平移的性质,故属平移;②用打气筒打气时,气筒里活塞沿直线运动,符合平移的性质,故属平移;③随风摆动的旗帜,在运动的过程中改变图形的形状,不符合平移的性质;④小河里流动的水流,在运动的过程中改变图形的方向,不符合平移的性质.故选B.【版权所有:21教育】
4.B
【解析】试题解析:根据题意,将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC;
又∵AB+BC+AC=8,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.
故选B.
5.C
【解析】试题解析:∵△ABC沿AB方向平移至△DEF,平移的距离是AD,
∴AD=CE,
∵BF=CE
∴AD= BF
∴AD=(AF-DB )÷2=(8-2)÷2=3.
故选C.
6.A
【解析】解:平移不改变图形的形状和大小,故线段的长度不变,长度是3cm.故选A.
7.B
【解析】∵△ABE向右平移得到△DCF,
∴AB∥CD,AE∥DF,
∴∠DCF=∠B=45°,
∴∠CDF=180°-45°-60°=75°,
∴∠AGC=180°-75°=105°
故选B.
8.C
【解析】解:因为经过平移两个图形可变为两个边长相等长方形,所以两人用的一样多.故选C.
点睛:本题主要考查的是平移的性质、熟练掌握平移的性质是解题的关键.
9.A
【解析】由图知B(4,1)移动以后,B1(0,3)所以,横坐标向下移动4个单位,纵坐标向上移动2个单位,P(a,b) 移动以后 P1(a-4,b+2),所以选A.21世纪教育网版权所有
点睛:点的平移
直角坐标系下将点(x,y)向右(或左)平移a个单位长度,对应点的横坐标加上a,(或减去a),纵坐标不变(x+a,y)或(x-a,y).21·cn·jy·com
直角坐标系下将点(x,y)向上(或下)平移a个单位长度,对应点的纵坐标加上a,(或减去a),横坐标不变(x,y+a)或(x,y-a).【来源:21cnj*y.co*m】
二、填空题
10.16
【解析】由题意可知小路的面积为:8×2=16,
故答案为:16.
11.25°
【解析】试题解析:∵将△ABC平移到达△的位置,
∴△ACB≌△,BC∥
∵∠ABC=55°,∠ACB=100°,
∴∠=55°,∠=100°,
则∠的度数为:180°-100°-55°=25°.
12.10cm
【解析】根据平移的性质得:AB=CD=3,AC=BD=2,则四边形ABDC的周长3+3+2+2=10.
【方法点睛】本题目是一道涉及平移的题目,运用了平移的性质——平移前后两个图形的对应边平行且相等,每对对应点的连线平行且相等.【出处:21教育名师】
13.5
【解析】∵平移只改变图形的位置,不改变图形的大小和形状,
∴图中的三角形1,2,3,4,5都可以由△ABC平移得到.故答案为5.
14.6
【解析】阴影部分为长方形,根据平移的性质可得阴影部分是长为3,宽为2,让长乘宽即为阴影部分的面积.
解:易知,当正方形ABCD向上平移2cm。则阴影长方形的宽=4-2=2cm 向右平移1cm则阴影长方形的长=4-1=3cm 所以阴影部分面积=2×3=6cm “点睛”本题难度较低,主要考查学生对平移知识点的掌握。要注意数形结合思想的培养,运用到考试中去。21cnjy.com
15.402.
【解析】根据平移的性质得出AA1=5,A1A2=5,A2B1=A1B1-A1A2=6-5=1,进而求出AB1和AB2的长,然后根据所求得出数字变化规律,进而得出ABn=(n+1)×5+1求出n即可.
解:∵AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,
∴AA1=5,A1A2=5,A2B1=A1B1?A1A2=6?5=1,
∴AB1=AA1+A1A2+A2B1=5+5+1=11=2×5+1,
∴AB2的长为:5+5+6=16=3×5+1;
……
∴ABn=(n+1)×5+1=2016,
解得:n=402.
故答案为:402.
点睛:本题主要考查找规律.根据所求出的数字找出其变化规律是解题的关键.
16.20
【解析】∵将ABC向右平移5个单位后得到DEF,
∴AD//CF,AD=CF=5,
∴四边形ACFD是平行四边形,
∴S平行四边形ACFD=.
故答案是:20.
三、解答题
17.(1)作图见解析;(2)点A′的坐标是(-1,-1),点B′的坐标是(-3,-3),点C′的坐标是(2,-4);(3)5.21·世纪*教育网
【解析】试题分析:(1)根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置,然后顺次连接即可;2-1-c-n-j-y
(2)根据平面直角坐标系写出各点的坐标即可;
(3)根据图形得到△ABC的底边AB和AB边上的高,利用三角形的面积公式列式计算即可得解.
试题解析:(1)画图如下,
(2)点A′的坐标是(-1,-1),点B′的坐标是(-3,-3),
点C′的坐标是(2,-4);
(3).
18.四边形DEBM的面积是39.
【解析】试题分析:先判断出四边形DEBM面积等于梯形ACFM的面积,再根据平移变化只改变图形的位置不改变图形的形状可得DF=CA,然后求出MF,根据平移的距离求出CF=6,然后利用梯形的面积公式列式计算即可得解.2·1·c·n·j·y
试题解析:
∵两个三角形大小一样,
∴四边形DEBM面积等于梯形ACFM的面积,
由平移的性质得,DF=AC,FC=6,
∵AC=8,DM=3,
∴MF=DF-DM=8-3=5,
∴四边形DEBM面积= (5+8)×6=39.
点睛:本题考查了平移的性质,对应点连线的长度等于平移距离,平移变化只改变图形的位置不改变图形的形状,熟记性质并判断出四边形DEBM面积等于梯形ACFM的面积是解题的关键.www-2-1-cnjy-com
19.(1) ①作图见解析;②作图见解析.
(2)作图见解析
【解析】试题分析:(1)①过点C作AB的垂线段,垂足为F,CF就是所求,理由是垂线段最短;②作点C关于小河AB的对称点M,连接MD,交l于点H,所求的路线为C→H→D,理由是两点之间线段最短.21*cnjy*com
(2)直接根据图形平移的性质作出平移后的图形即可
试题解析:(1)①如图,
理由是:垂线段最短.
②如图,
理由是:两点之间线段最短.
(2)如图,
20.(1)画图见解析;(2)画图见解析;(3)平行且相等;(4)12;(5)9
【解析】试题分析:(1)利用网格特点和平移的性质分别画出点A、B、C的对应点A′、B′、C′即可得到△A′B′C′;【来源:21·世纪·教育·网】
(2)找出线段A′C′的中点E′,连接B′E′;
(3)根据平移的性质求解;
(4)由于线段AB扫过的部分为平行四边形,则根据平行四边形的面积公式可求解.
(5)根据同底等高面积相等可知共有9个点.
试题解析:
(1)△A′B′C′如图所示;
(2)B′D′如图所示;
(3)BB′∥CC′,BB′=CC′;
(4)线段AB扫过的面积=4×3=12;
(5)有9个点.
【点睛】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
21.解:由平移的性质可知:铺设主要楼梯所需红地毯的长至少为5.8+ 2.5=8.4(m),由主楼梯宽为2m,则 地毯面积至少为8.4 ×2=16.8(m2), 所以购买这种地毯至少需要16.8×30=504(元).
姓名________________考号_________总分____________
本节应掌握和应用的知识
平移:把一个图形整体沿某一直线方向移动 ,叫平移.
2. 平移的性质
(1)新图形与原图形形状、大小完全相同;
(2)新图形上的每一点都是由它的对应点平移后得到的;
(3)连接各组对应点的线段平行(或在同一条直线上)且相等 .
基础知识和能力拓展训练
一、选择题
1.下列现象中是平移的是( )
A. 将一张纸沿它的中线折叠????? B. 飞碟的快速转动?????
C. 电梯的上下移动????? D. 翻开书中的每一页纸张
2.下列选项中能由左图平移得到的是( )
A. B. C. D.
3.在以下现象中:①在笔直的公路上行驶的汽车;②用打气筒给自行车打气时,气筒里活塞的运动;③随风摆动的旗帜;④小河里流动的水流.属于平移的是( )
A.① B.①② C.①②③ D.①②③④
4.如图,将△ABC沿BC方向平移1个单位得到△DEF,若△ABC的周长等于8,则四边形ABFD的周长等于( )www.21-cn-jy.com
A. 9 B. 10 C. 11 D. 12
5.如图,将△ABC沿AB方向向右平移得到△DEF,其中AF=8,DB=2,则平移的距离为( )
A. 5 B. 4 C. 3 D. 2
6.将长度为3cm的线段向上平移20cm,所得线段的长度是( )
A. 3cm B. 23cm C. 20cm D. 17cm
7.如图,将△ABE向右平移得到△DCF, 与交于点,其中, ,则( ).
A. B. C. D.
8.小明和小华在手工制作课上用铁丝制作楼梯模型,如图,那么他们两个人用的铁丝( )
A. 小华用的多 B. 小明用的多 C. 两人用的一样多 D. 不能确定谁用的多
9.如图,线段AB经过平移得到线段A1B1,其中A,B的对应点分别为A1,B1,这四个点都在格点上.若线段AB上有一个点P(a,b),则点P在A1B1上的对应点P1的坐标为( )
A. (a-4,b+2) B. (a-4,b-2) C. (a+4,b+2) D. (a+4,b-2)
二、填空题
10.在如图所示的草坪上,铺设一条宽为2的小路,则小路的面积___________.
11.如图,将△ABC平移到△A′B′C′的位置(点B′在AC边上),若∠B=55°,∠C=100°,则∠AB′A′的度数为________________°21教育名师原创作品
12.如图,将线段AB沿箭头方向平移2 cm得到线段CD,若AB=3 cm,则四边形ABDC的周长为___cm.
13.如图所示,由三角形ABC平移得到的三角形有_______个.
14.如图,边长为4cm 的正方形ABCD先向上平移2cm,再向右平移1cm,得到正方形,此时阴影部分的面积为_______________cm2.
15.如图,长方形ABCD中,AB=6,第一次平移长方形ABCD沿AB的方向向右平移5个单位长度,得到长方形A1B1C1D1,第2次平移长方形A1B1C1D1沿A1B1的方向向右平移5个单位长度,得到长方形A2B2C2D2,…,第n次平移长方形An-1Bn-1Cn-1Dn-1沿An-1Bn-1的方向向右平移5个单位长度,得到长方形AnBnCnDn(n>2),若ABn的长度为2 016,则n的值为__________.
16.如图,已知ABC中, B=90,BC=3,AB=4,将ABC向右平移5个单位后得到DEF,则四边形ACFD的面积是_______.
三、解答题
17.如图,将△ABC先向下平移5个单位再向左平移4个单位,画出平移后的△A′B′C′
(1)写出点A′、B′、C′的坐标.
(2)求△A′B′C′的面积.
18.如图,将直角△沿着射线的方向平移到△的位置.已知AC=8,DM=3,平移的距离为6,求四边形的面积. 21教育网
19.(1)如图所示,小明准备在C处牵牛到河边AB饮水,按下列要求作图并说明理由.
①请用三角板作出小明的最短路线(不考虑其他因素);
②如图乙,若小明在C处牵牛到河边AB饮水,并且必须到河边D处观察河水的水质情况,请作出小明行走的最短路线。
(2)经过平移,图中左边图形上A点移到E点,作出平移后的图形。
理由: ;理由: 。
20.如图,网格中每个小正方形边长为1,△ABC的顶点都在格点上.将△ABC向左平移2格,再向上平移3格,得到△A′B′C′.
(1)请在图中画出平移后的△A′B′C′;
(2)画出平移后的△A′B′C′的中线B′D′
(3)若连接BB′,CC′,则这两条线段的关系是________
(4)△ABC在整个平移过程中线段AB 扫过的面积为________
(5)若△ABC与△ABE面积相等,则图中满足条件且异于点C的格点E共有______个
(注:格点指网格线的交点)
21. 白云宾馆在装修时,准备在主楼梯上铺上红地毯,已知这种地毯每平方米售价30元,主楼梯宽2m,其侧面如图所示,则购买这种地毯至少需要多少元?21*cnjy*com
参考答案
1.C
【解析】A. 将一张纸沿它的中线折叠,不符合平移定义,故本选项错误;
B. 飞蝶的快速转动,不符合平移定义,故本选项错误;
C. 电梯的上下移动,符合平移的定义,正确;
D. 翻开书中的每一页纸张,不符合平移的定义,故本选项错误。
故选C.
2.C
【解析】试题解析:能由左图平移得到的是:选项C. 故选C.
3.B
【解析】①在笔直的公路上行驶的汽车沿直线运动,符合平移的性质,故属平移;②用打气筒打气时,气筒里活塞沿直线运动,符合平移的性质,故属平移;③随风摆动的旗帜,在运动的过程中改变图形的形状,不符合平移的性质;④小河里流动的水流,在运动的过程中改变图形的方向,不符合平移的性质.故选B.【版权所有:21教育】
4.B
【解析】试题解析:根据题意,将周长为8个单位的△ABC沿边BC向右平移1个单位得到△DEF,
∴AD=1,BF=BC+CF=BC+1,DF=AC;
又∵AB+BC+AC=8,
∴四边形ABFD的周长=AD+AB+BF+DF=1+AB+BC+1+AC=10.
故选B.
5.C
【解析】试题解析:∵△ABC沿AB方向平移至△DEF,平移的距离是AD,
∴AD=CE,
∵BF=CE
∴AD= BF
∴AD=(AF-DB )÷2=(8-2)÷2=3.
故选C.
6.A
【解析】解:平移不改变图形的形状和大小,故线段的长度不变,长度是3cm.故选A.
7.B
【解析】∵△ABE向右平移得到△DCF,
∴AB∥CD,AE∥DF,
∴∠DCF=∠B=45°,
∴∠CDF=180°-45°-60°=75°,
∴∠AGC=180°-75°=105°
故选B.
8.C
【解析】解:因为经过平移两个图形可变为两个边长相等长方形,所以两人用的一样多.故选C.
点睛:本题主要考查的是平移的性质、熟练掌握平移的性质是解题的关键.
9.A
【解析】由图知B(4,1)移动以后,B1(0,3)所以,横坐标向下移动4个单位,纵坐标向上移动2个单位,P(a,b) 移动以后 P1(a-4,b+2),所以选A.21世纪教育网版权所有
点睛:点的平移
直角坐标系下将点(x,y)向右(或左)平移a个单位长度,对应点的横坐标加上a,(或减去a),纵坐标不变(x+a,y)或(x-a,y).21·cn·jy·com
直角坐标系下将点(x,y)向上(或下)平移a个单位长度,对应点的纵坐标加上a,(或减去a),横坐标不变(x,y+a)或(x,y-a).【来源:21cnj*y.co*m】
二、填空题
10.16
【解析】由题意可知小路的面积为:8×2=16,
故答案为:16.
11.25°
【解析】试题解析:∵将△ABC平移到达△的位置,
∴△ACB≌△,BC∥
∵∠ABC=55°,∠ACB=100°,
∴∠=55°,∠=100°,
则∠的度数为:180°-100°-55°=25°.
12.10cm
【解析】根据平移的性质得:AB=CD=3,AC=BD=2,则四边形ABDC的周长3+3+2+2=10.
【方法点睛】本题目是一道涉及平移的题目,运用了平移的性质——平移前后两个图形的对应边平行且相等,每对对应点的连线平行且相等.【出处:21教育名师】
13.5
【解析】∵平移只改变图形的位置,不改变图形的大小和形状,
∴图中的三角形1,2,3,4,5都可以由△ABC平移得到.故答案为5.
14.6
【解析】阴影部分为长方形,根据平移的性质可得阴影部分是长为3,宽为2,让长乘宽即为阴影部分的面积.
解:易知,当正方形ABCD向上平移2cm。则阴影长方形的宽=4-2=2cm 向右平移1cm则阴影长方形的长=4-1=3cm 所以阴影部分面积=2×3=6cm “点睛”本题难度较低,主要考查学生对平移知识点的掌握。要注意数形结合思想的培养,运用到考试中去。21cnjy.com
15.402.
【解析】根据平移的性质得出AA1=5,A1A2=5,A2B1=A1B1-A1A2=6-5=1,进而求出AB1和AB2的长,然后根据所求得出数字变化规律,进而得出ABn=(n+1)×5+1求出n即可.
解:∵AB=6,第1次平移将矩形ABCD沿AB的方向向右平移5个单位,得到矩形A1B1C1D1,
第2次平移将矩形A1B1C1D1沿A1B1的方向向右平移5个单位,得到矩形A2B2C2D2…,
∴AA1=5,A1A2=5,A2B1=A1B1?A1A2=6?5=1,
∴AB1=AA1+A1A2+A2B1=5+5+1=11=2×5+1,
∴AB2的长为:5+5+6=16=3×5+1;
……
∴ABn=(n+1)×5+1=2016,
解得:n=402.
故答案为:402.
点睛:本题主要考查找规律.根据所求出的数字找出其变化规律是解题的关键.
16.20
【解析】∵将ABC向右平移5个单位后得到DEF,
∴AD//CF,AD=CF=5,
∴四边形ACFD是平行四边形,
∴S平行四边形ACFD=.
故答案是:20.
三、解答题
17.(1)作图见解析;(2)点A′的坐标是(-1,-1),点B′的坐标是(-3,-3),点C′的坐标是(2,-4);(3)5.21·世纪*教育网
【解析】试题分析:(1)根据网格结构找出点A、B、C平移后的对应点A′、B′、C′的位置,然后顺次连接即可;2-1-c-n-j-y
(2)根据平面直角坐标系写出各点的坐标即可;
(3)根据图形得到△ABC的底边AB和AB边上的高,利用三角形的面积公式列式计算即可得解.
试题解析:(1)画图如下,
(2)点A′的坐标是(-1,-1),点B′的坐标是(-3,-3),
点C′的坐标是(2,-4);
(3).
18.四边形DEBM的面积是39.
【解析】试题分析:先判断出四边形DEBM面积等于梯形ACFM的面积,再根据平移变化只改变图形的位置不改变图形的形状可得DF=CA,然后求出MF,根据平移的距离求出CF=6,然后利用梯形的面积公式列式计算即可得解.2·1·c·n·j·y
试题解析:
∵两个三角形大小一样,
∴四边形DEBM面积等于梯形ACFM的面积,
由平移的性质得,DF=AC,FC=6,
∵AC=8,DM=3,
∴MF=DF-DM=8-3=5,
∴四边形DEBM面积= (5+8)×6=39.
点睛:本题考查了平移的性质,对应点连线的长度等于平移距离,平移变化只改变图形的位置不改变图形的形状,熟记性质并判断出四边形DEBM面积等于梯形ACFM的面积是解题的关键.www-2-1-cnjy-com
19.(1) ①作图见解析;②作图见解析.
(2)作图见解析
【解析】试题分析:(1)①过点C作AB的垂线段,垂足为F,CF就是所求,理由是垂线段最短;②作点C关于小河AB的对称点M,连接MD,交l于点H,所求的路线为C→H→D,理由是两点之间线段最短.21*cnjy*com
(2)直接根据图形平移的性质作出平移后的图形即可
试题解析:(1)①如图,
理由是:垂线段最短.
②如图,
理由是:两点之间线段最短.
(2)如图,
20.(1)画图见解析;(2)画图见解析;(3)平行且相等;(4)12;(5)9
【解析】试题分析:(1)利用网格特点和平移的性质分别画出点A、B、C的对应点A′、B′、C′即可得到△A′B′C′;【来源:21·世纪·教育·网】
(2)找出线段A′C′的中点E′,连接B′E′;
(3)根据平移的性质求解;
(4)由于线段AB扫过的部分为平行四边形,则根据平行四边形的面积公式可求解.
(5)根据同底等高面积相等可知共有9个点.
试题解析:
(1)△A′B′C′如图所示;
(2)B′D′如图所示;
(3)BB′∥CC′,BB′=CC′;
(4)线段AB扫过的面积=4×3=12;
(5)有9个点.
【点睛】本题考查了作图-平移变换:确定平移后图形的基本要素有两个:平移方向、平移距离.作图时要先找到图形的关键点,分别把这几个关键点按照平移的方向和距离确定对应点后,再顺次连接对应点即可得到平移后的图形.
21.解:由平移的性质可知:铺设主要楼梯所需红地毯的长至少为5.8+ 2.5=8.4(m),由主楼梯宽为2m,则 地毯面积至少为8.4 ×2=16.8(m2), 所以购买这种地毯至少需要16.8×30=504(元).
