人教版七年级上册第三章一元一次方程3.1.2 等式的性质等式的性质 课件
文档属性
| 名称 | 人教版七年级上册第三章一元一次方程3.1.2 等式的性质等式的性质 课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 206.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-02 00:00:00 | ||
图片预览



文档简介
课件13张PPT。第三章 一元一次方程
等式的性质1.什么是方程?方程是含有未知数 的等式. 2.指出下列式子中,哪些是方程,哪些不是,并说明理由.3 + x = 5;
3x + 2y = 7;
2 + 3 = 3 + 2;
a + b = b + a (a、b已知);
5x + 7 = 3x – 5.3.上面的式子有哪些共同特点?都是等式.我们可以用a = b来表示一般的等式.一、创设情境,复习导入(1)3x-5=21;
(2)0.28-0.13y=0.27y+1. 用估算的方法可以求出简单的一元一次方程的解.
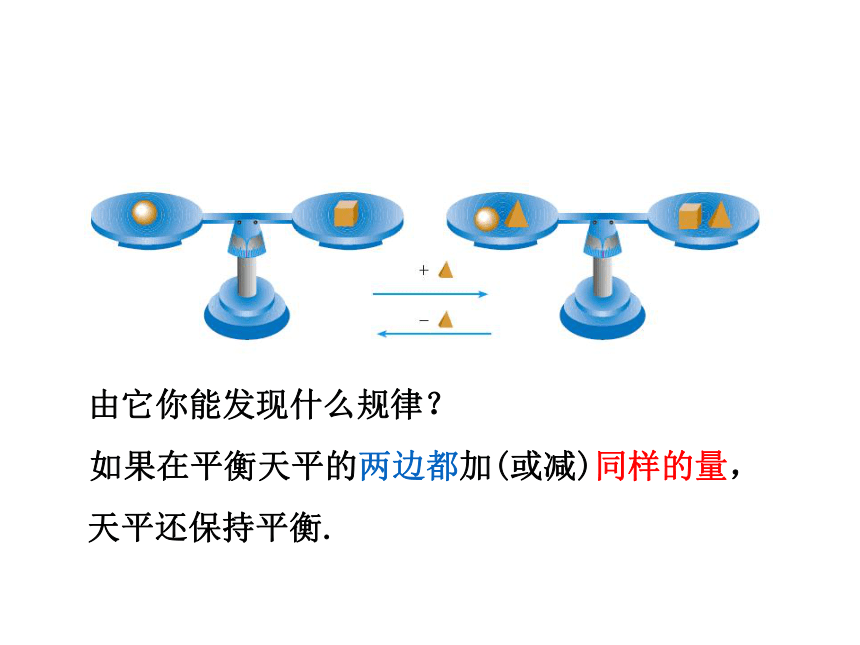
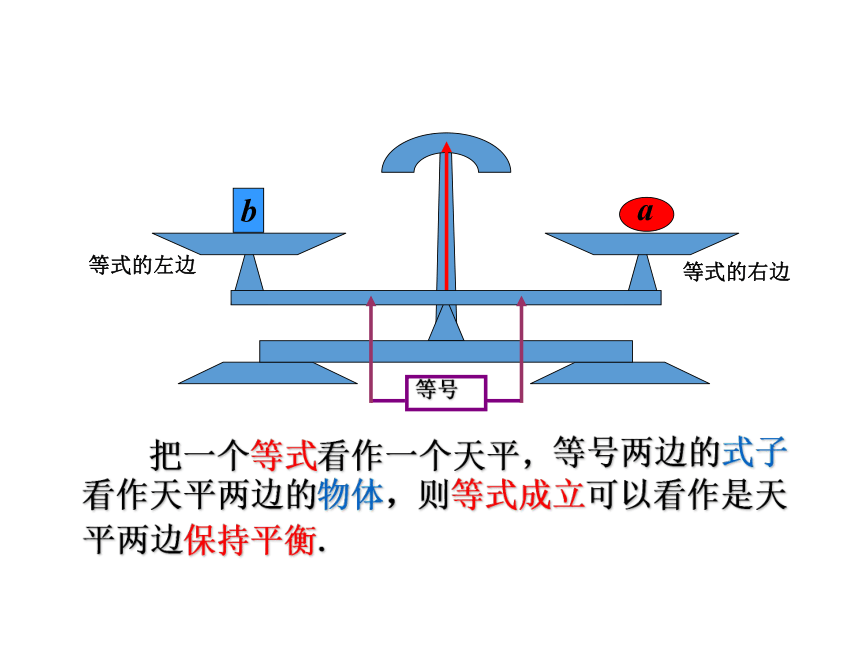
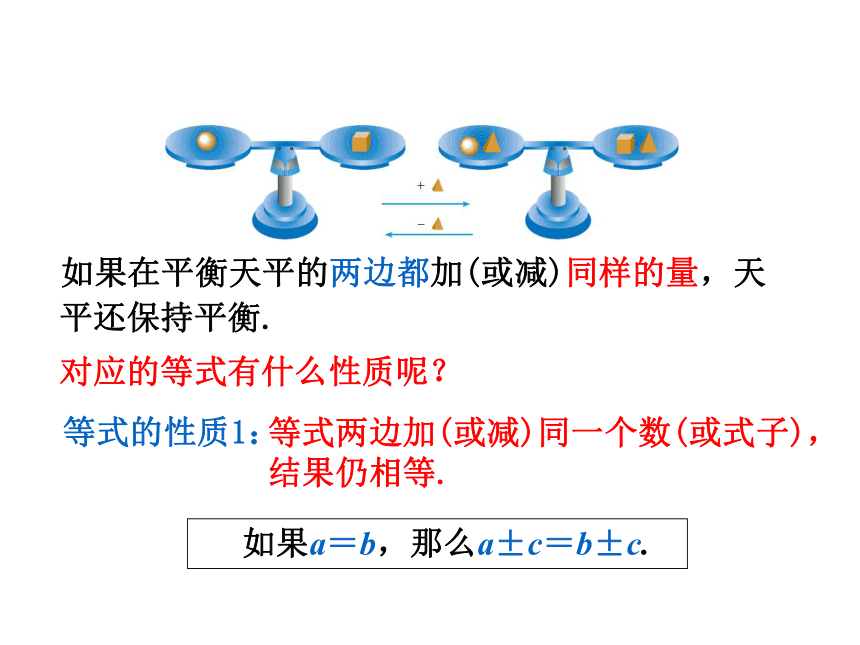
你能用估算的方法求出下列方程的解吗? 用估算的方法解比较复杂的方程是困难的.因此,我们需要讨论怎样解方程.一、创设情境,复习导入二、操作实验,探究新知由它你能发现什么规律?如果在平衡天平的两边都加(或减)同样的量,天平还保持平衡.二、操作实验,探究新知把一个等式看作一个天平,等式的左边等式的右边等号两边的式子看作天平两边的物体,则等式成立可以看作是天平两边保持平衡.二、操作实验,探究新知等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等. 如果a=b,那么a±c=b±c.对应的等式有什么性质呢?如果在平衡天平的两边都加(或减)同样的量,天平还保持平衡.二、操作实验,探究新知等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等. 如果a=b,那么ac=bc;
如果a=b(c≠0),那么对应的等式有什么性质呢?如果在平衡天平的两边都扩大(或缩小)相同的倍数,天平还保持平衡.二、操作实验,探究新知2.等式两边加或减,乘或除以的数一定是同一个数3.等式两边不能都除以0,因为0不能作除数(分母).1.等式两边都要参加运算,并且是作同一种运算.注意:等式的性质1: 如果a=b,那么a±c=b±c.等式的性质2: 如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .或同一个式子.三、应用举例,学以致用 学习了等式的性质后,小红发现运用等式的性质可使复杂的等式变得简洁,这使她异常兴奋. 她随手写了一个等式3a+b-2=7a+b-2,并用等式的性质对这个等式进行变形,过程如下: 两边加2,得 3a+b=7a+b. 两边减b,得 3a=7a.两边除以a,得 3=7. 小红感到很惊讶:居然能得出这样的等式!于是小红开始检查自己的变形过程,但怎么也找不出错误. 聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?三、应用举例,学以致用五、尝试练习,巩固性质练习:
已知2a-3=2b+1,试用等式的性质判断a和b的大小.a>b1.对自己说,你有什么收获?六、课堂小结,梳理新知2.对同学说,你有什么温馨提示?3.对老师说,你还有什么困惑?七、布置作业,深化新知3.作业:教科书习题3.1第8、9题. 1.如图a和图b分别表示两架处于平衡状态的简易天平,对a,b,c三种物体的质量判断正确的是( ).
A.a<c<b B.a<b<c C.c<b<a D.b<a<c 2.(1)方程x+3=1-2x变形为x+2x=1-3的依据是 .
(2)已知 ,可求得x= ,这是根据 .
等式的性质1.什么是方程?方程是含有未知数 的等式. 2.指出下列式子中,哪些是方程,哪些不是,并说明理由.3 + x = 5;
3x + 2y = 7;
2 + 3 = 3 + 2;
a + b = b + a (a、b已知);
5x + 7 = 3x – 5.3.上面的式子有哪些共同特点?都是等式.我们可以用a = b来表示一般的等式.一、创设情境,复习导入(1)3x-5=21;
(2)0.28-0.13y=0.27y+1. 用估算的方法可以求出简单的一元一次方程的解.
你能用估算的方法求出下列方程的解吗? 用估算的方法解比较复杂的方程是困难的.因此,我们需要讨论怎样解方程.一、创设情境,复习导入二、操作实验,探究新知由它你能发现什么规律?如果在平衡天平的两边都加(或减)同样的量,天平还保持平衡.二、操作实验,探究新知把一个等式看作一个天平,等式的左边等式的右边等号两边的式子看作天平两边的物体,则等式成立可以看作是天平两边保持平衡.二、操作实验,探究新知等式的性质1:等式两边加(或减)同一个数(或式子),结果仍相等. 如果a=b,那么a±c=b±c.对应的等式有什么性质呢?如果在平衡天平的两边都加(或减)同样的量,天平还保持平衡.二、操作实验,探究新知等式的性质2:等式两边乘同一个数,或除以同一个不为0的数,结果仍相等. 如果a=b,那么ac=bc;
如果a=b(c≠0),那么对应的等式有什么性质呢?如果在平衡天平的两边都扩大(或缩小)相同的倍数,天平还保持平衡.二、操作实验,探究新知2.等式两边加或减,乘或除以的数一定是同一个数3.等式两边不能都除以0,因为0不能作除数(分母).1.等式两边都要参加运算,并且是作同一种运算.注意:等式的性质1: 如果a=b,那么a±c=b±c.等式的性质2: 如果a=b,那么ac=bc;
如果a=b(c≠0),那么 .或同一个式子.三、应用举例,学以致用 学习了等式的性质后,小红发现运用等式的性质可使复杂的等式变得简洁,这使她异常兴奋. 她随手写了一个等式3a+b-2=7a+b-2,并用等式的性质对这个等式进行变形,过程如下: 两边加2,得 3a+b=7a+b. 两边减b,得 3a=7a.两边除以a,得 3=7. 小红感到很惊讶:居然能得出这样的等式!于是小红开始检查自己的变形过程,但怎么也找不出错误. 聪明的同学,你能让小红的愁眉在恍然大悟中舒展开来吗?三、应用举例,学以致用五、尝试练习,巩固性质练习:
已知2a-3=2b+1,试用等式的性质判断a和b的大小.a>b1.对自己说,你有什么收获?六、课堂小结,梳理新知2.对同学说,你有什么温馨提示?3.对老师说,你还有什么困惑?七、布置作业,深化新知3.作业:教科书习题3.1第8、9题. 1.如图a和图b分别表示两架处于平衡状态的简易天平,对a,b,c三种物体的质量判断正确的是( ).
A.a<c<b B.a<b<c C.c<b<a D.b<a<c 2.(1)方程x+3=1-2x变形为x+2x=1-3的依据是 .
(2)已知 ,可求得x= ,这是根据 .
