5.1.2垂线(课件)
图片预览







文档简介
(共32张PPT)
5.1.2垂线
人教版 七年级下
学习目标
1.在生动有趣的情境中,通过画、折等活动,进一步丰富对两条直线互相垂直的认识,掌握有关的符号表示。
2.会借助三角尺、量角器、方格纸画垂线,进一步丰富操作活动经验。
3.通过操作活动,探索有关垂直的一些性质。
一、实验探究
垂 直
1、在相交线的模型中,固定木条a,转动木条b。
⑴ 当 b 的位置变化时, a, b所成的角α也会发生变化。
a
b
转 动
⑵ 当 α=90°时,
a 与 b 互相垂直
90°
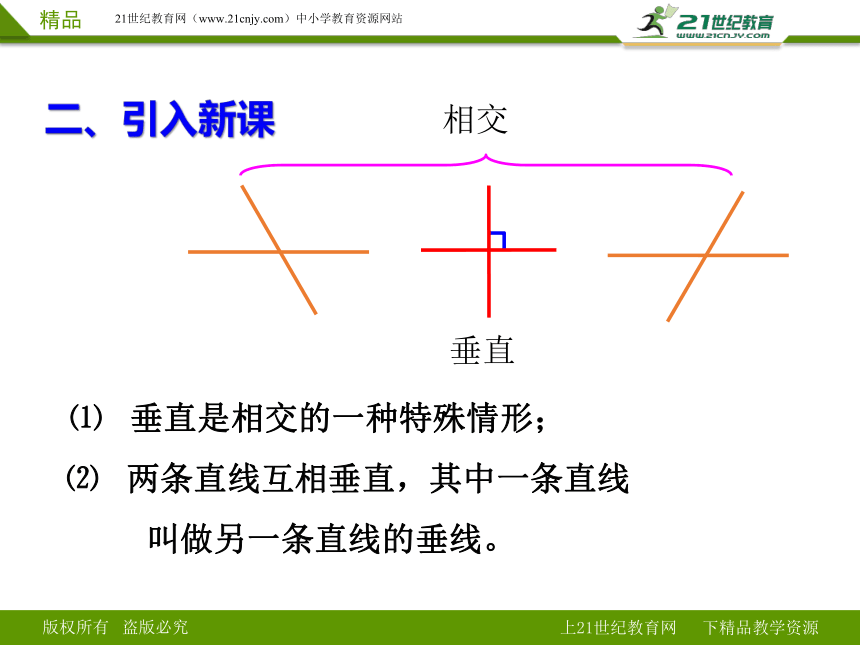
⑴ 垂直是相交的一种特殊情形;
相交
垂直
⑵ 两条直线互相垂直,其中一条直线
叫做另一条直线的垂线。
二、引入新课
⑴ 垂直是相交的一种特殊情形;
⑵ 两条直线互相垂直,其中一条直线
叫做另一条直线的垂线。
⑶ 它们的交点叫做垂足;
A
B
C
D
O
如图,直线 AB⊥CD
垂足为 O
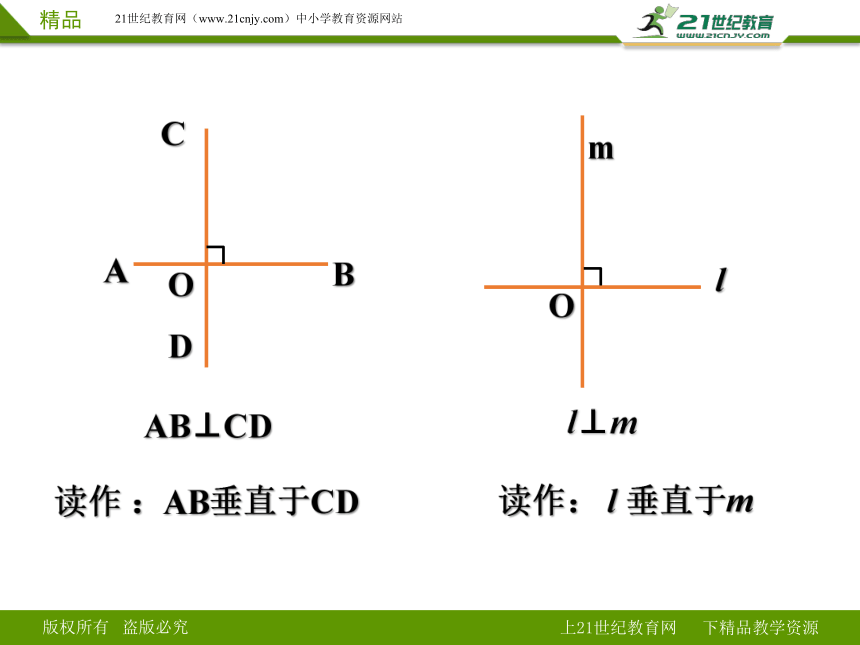
三、垂直的表示方法
l⊥m
AB⊥CD
O
D
C
A
B
m
l
O
读作 :AB垂直于CD
读作: l 垂直于m
A
B
C
D
O
根据两条直线垂直的定义可知:
如果两条直线相交所成的四个角中的任意一个角等于90°,那么这两条直线垂直。
如图,如果直线AB、CD相交于点O,∠AOC=90°,
那么AB⊥CD.
A
B
C
D
O
如图,如果直线AB、CD相交于点O,∠AOC=90°,
那么AB⊥CD.
这个推理过程可以写成下面形式:
∵∠AOC=90°
∴ AB⊥CD
(垂直的定义)
四、垂直的推理书写
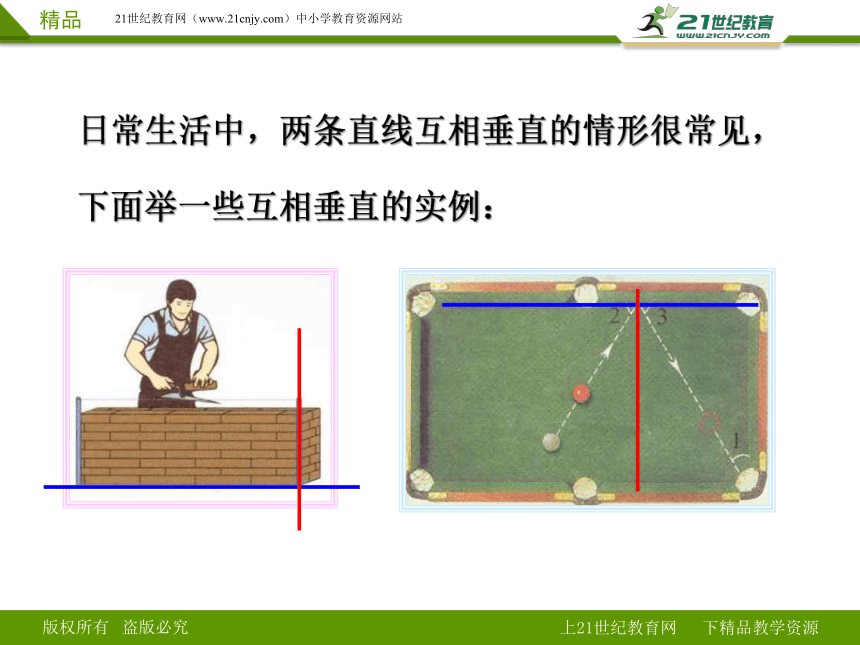
日常生活中,两条直线互相垂直的情形很常见,
下面举一些互相垂直的实例:
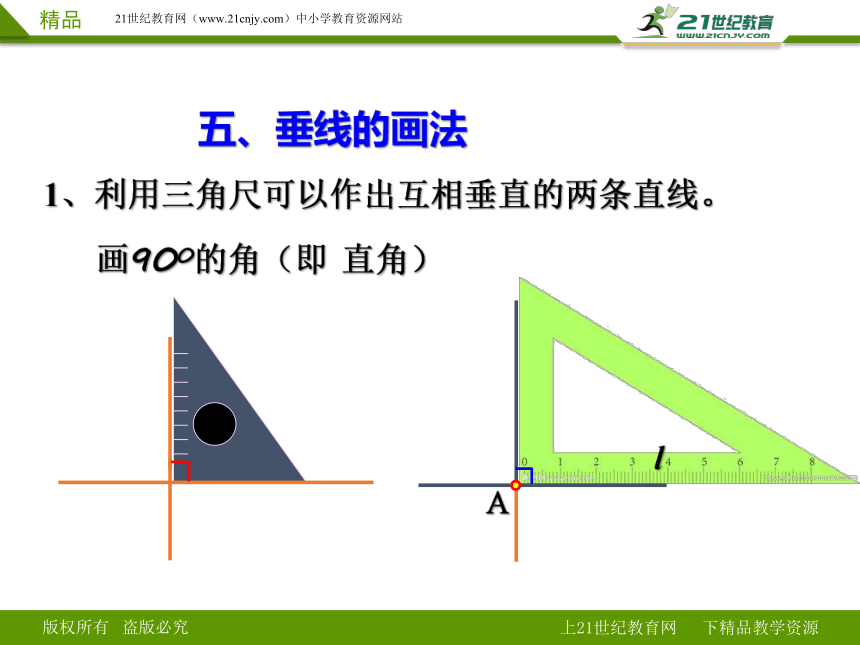
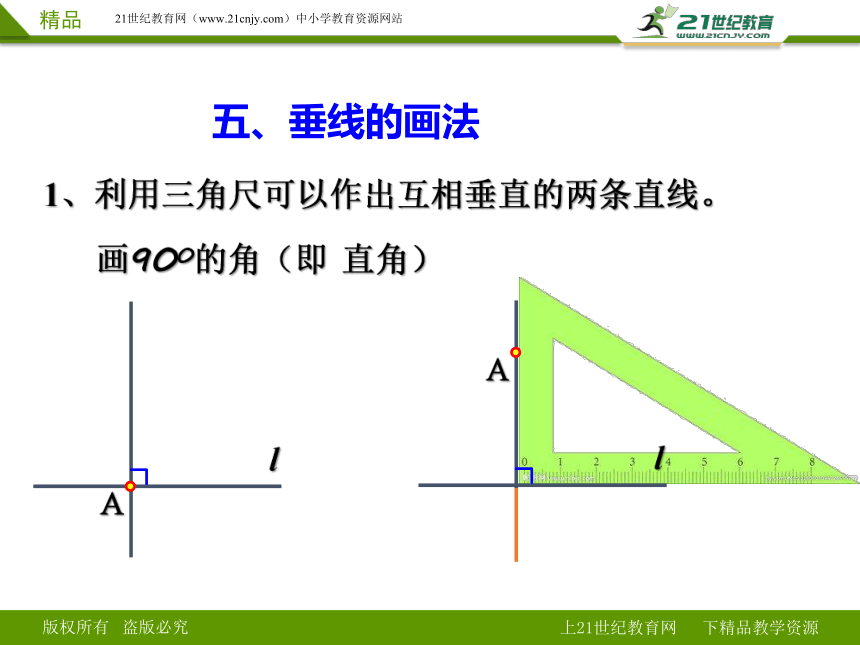
1、利用三角尺可以作出互相垂直的两条直线。
画900的角(即 直角)
五、垂线的画法
l
A
1、利用三角尺可以作出互相垂直的两条直线。
画900的角(即 直角)
五、垂线的画法
l
A
l
A
【问题】⑴ 过直线 l 上一点A作直线 l 的垂线,
你能作出多少条?
l
A
答:只能画出一条垂线。
【问题】⑵ 过直线 l 外一点A作直线 l 的垂线,
你能作出多少条?
l
A
答:只能画出一条垂线。
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线。
l
A
l
A
在同一平面内,过一点有且只有一条直线与已知直线垂直。
垂线的性质公理
1、找出下列各图中互相垂直的直线.
O
B
A
C
D
A
D
C
B
OA⊥OC
OB⊥OD
CD⊥AB
AC⊥BC
六、课堂练习
2. 利用方格纸可以用其中的横竖线作出互相垂直的两条直线,你还有其它方法吗?
3、画一条线段或射线的垂线,就是画它们所在的直线的垂线。如图,请你过点P画出射线AB或线段AB的垂线。
P
A
B
P
A
B
A
B
P
4、当两条直线相交所成的四个角都相等时,
这两条直线有什么位置关系?为什么?
O
D
C
A
B
∵∠AOC=∠BOC=∠BOD=∠AOD
解:这两条直线互相垂直,理由如下:
∴ 4∠AOC=360°
∴ ∠AOC=90°
∴ AB⊥CD
且∠AOC+∠BOC+∠BOD+∠AOD=360°
【思考】如图,在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?请你画图形。
P
H
【探究】如图,连接直线 l 外的一点P与直线l 上各点O,A1,A2,A3,···,其中PO⊥l (我们称PO为点P到直线的垂线段)。比较线段PO,PA1,PA2,PA3,···的长短,这些线段中,哪一条最短?
P
A1
A2
A3
A4
O
l
PO最短!
P
A1
A2
A3
A4
O
l
连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:
垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
课堂练习
1、画出下列各图中点P到直线AB的垂线段,指出
点P到直线AB的距离。
P
A
B
M
A
B
P
M
答:P到直线AB的距离是垂线段PM的长度。
2、如图,△ABC中,∠C=90°,△ABC的三条边AB,BC,CA哪条边最长?为什么?
A
C
B
答:边AB最长。理由如下 :
∵AC⊥BC
∴AC<AB
∵BC⊥AC
∴BC<AB
∴ AB、BC、CA中,边AB最长。
课堂练习
3、若A、B、C是直线 l 上的三点,P是直线 l 外一点,且PA=5cm,PB=4cm,PC=3cm,则点P到直线 l 的距离是【 】
(A)等于3cm; (B)大于3cm而小于4cm;
(C)不大于3cm; (D)小于3cm。
C
课堂练习
4、如图,点A、O、E在一条直线上,OB⊥AE,
OC⊥OD,则图中互余的角有 对,
互补的角有 对.
1
2
3
4
O
A
B
C
D
E
4
课堂练习
∠1+∠2=90°
解:互为余角有:
∠1+∠4=90°
∠3+∠2=90°
∠3+∠4=90°
4、如图,点A、O、E在一条直线上,OB⊥AE,
OC⊥OD,则图中互余的角有 对,
互补的角有 对.
1
2
3
4
O
A
B
C
D
E
4
5
课堂练习
∠1+∠COE=180°
解:互为补角有:
∠3+∠COE=180°
∠4+∠AOD=180°
∠2+∠AOD=180°
∠AOB+∠BOE=180°
5、如图,直线AB、EF相交于O,∠DOE=90°, ∠BOC=90°。说出∠AOD的余角、补角; ∠BOE的补角。
∠BOE的补角是:
∠AOE、 ∠COD、∠BOF
∠BOD、 ∠COE
∠AOE 、∠COD、∠BOF
答:∠AOD的余角有:
∠AOD的补角是:
A
O
B
C
D
E
F
6、直线AB、CD相交于O.
⑴OE、OF分别是∠AOC、 ∠BOD的平分线。画出这个图形。
A
B
C
D
O
F
E
⑵ 射线OE、OF在同一条直线上吗?
答: 射线OE、OF在同一条直线上。
6、直线AB、CD相交于O.
⑶ 画∠AOD的平分线OG,OE与OG有什么位置关系?
A
B
C
D
O
F
E
答: OG⊥OE。
G
一、垂线、垂直及表示方法、垂足、垂线段的概念
二、垂线的性质公理:
垂线的画法、点到直线的距离。
归纳与整理
在同一平面内,过一点有且只有一条直线与已知直线垂直。
垂线段最短。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
5.1.2垂线
人教版 七年级下
学习目标
1.在生动有趣的情境中,通过画、折等活动,进一步丰富对两条直线互相垂直的认识,掌握有关的符号表示。
2.会借助三角尺、量角器、方格纸画垂线,进一步丰富操作活动经验。
3.通过操作活动,探索有关垂直的一些性质。
一、实验探究
垂 直
1、在相交线的模型中,固定木条a,转动木条b。
⑴ 当 b 的位置变化时, a, b所成的角α也会发生变化。
a
b
转 动
⑵ 当 α=90°时,
a 与 b 互相垂直
90°
⑴ 垂直是相交的一种特殊情形;
相交
垂直
⑵ 两条直线互相垂直,其中一条直线
叫做另一条直线的垂线。
二、引入新课
⑴ 垂直是相交的一种特殊情形;
⑵ 两条直线互相垂直,其中一条直线
叫做另一条直线的垂线。
⑶ 它们的交点叫做垂足;
A
B
C
D
O
如图,直线 AB⊥CD
垂足为 O
三、垂直的表示方法
l⊥m
AB⊥CD
O
D
C
A
B
m
l
O
读作 :AB垂直于CD
读作: l 垂直于m
A
B
C
D
O
根据两条直线垂直的定义可知:
如果两条直线相交所成的四个角中的任意一个角等于90°,那么这两条直线垂直。
如图,如果直线AB、CD相交于点O,∠AOC=90°,
那么AB⊥CD.
A
B
C
D
O
如图,如果直线AB、CD相交于点O,∠AOC=90°,
那么AB⊥CD.
这个推理过程可以写成下面形式:
∵∠AOC=90°
∴ AB⊥CD
(垂直的定义)
四、垂直的推理书写
日常生活中,两条直线互相垂直的情形很常见,
下面举一些互相垂直的实例:
1、利用三角尺可以作出互相垂直的两条直线。
画900的角(即 直角)
五、垂线的画法
l
A
1、利用三角尺可以作出互相垂直的两条直线。
画900的角(即 直角)
五、垂线的画法
l
A
l
A
【问题】⑴ 过直线 l 上一点A作直线 l 的垂线,
你能作出多少条?
l
A
答:只能画出一条垂线。
【问题】⑵ 过直线 l 外一点A作直线 l 的垂线,
你能作出多少条?
l
A
答:只能画出一条垂线。
经过一点(已知直线上或直线外),能画出已知直线的一条垂线,并且只能画出一条垂线。
l
A
l
A
在同一平面内,过一点有且只有一条直线与已知直线垂直。
垂线的性质公理
1、找出下列各图中互相垂直的直线.
O
B
A
C
D
A
D
C
B
OA⊥OC
OB⊥OD
CD⊥AB
AC⊥BC
六、课堂练习
2. 利用方格纸可以用其中的横竖线作出互相垂直的两条直线,你还有其它方法吗?
3、画一条线段或射线的垂线,就是画它们所在的直线的垂线。如图,请你过点P画出射线AB或线段AB的垂线。
P
A
B
P
A
B
A
B
P
4、当两条直线相交所成的四个角都相等时,
这两条直线有什么位置关系?为什么?
O
D
C
A
B
∵∠AOC=∠BOC=∠BOD=∠AOD
解:这两条直线互相垂直,理由如下:
∴ 4∠AOC=360°
∴ ∠AOC=90°
∴ AB⊥CD
且∠AOC+∠BOC+∠BOD+∠AOD=360°
【思考】如图,在灌溉时,要把河中的水引到农田P处,如何挖渠能使渠道最短?请你画图形。
P
H
【探究】如图,连接直线 l 外的一点P与直线l 上各点O,A1,A2,A3,···,其中PO⊥l (我们称PO为点P到直线的垂线段)。比较线段PO,PA1,PA2,PA3,···的长短,这些线段中,哪一条最短?
P
A1
A2
A3
A4
O
l
PO最短!
P
A1
A2
A3
A4
O
l
连接直线外一点与直线上各点的所有线段中,垂线段最短。
简单说成:
垂线段最短。
直线外一点到这条直线的垂线段的长度,叫做点到直线的距离。
课堂练习
1、画出下列各图中点P到直线AB的垂线段,指出
点P到直线AB的距离。
P
A
B
M
A
B
P
M
答:P到直线AB的距离是垂线段PM的长度。
2、如图,△ABC中,∠C=90°,△ABC的三条边AB,BC,CA哪条边最长?为什么?
A
C
B
答:边AB最长。理由如下 :
∵AC⊥BC
∴AC<AB
∵BC⊥AC
∴BC<AB
∴ AB、BC、CA中,边AB最长。
课堂练习
3、若A、B、C是直线 l 上的三点,P是直线 l 外一点,且PA=5cm,PB=4cm,PC=3cm,则点P到直线 l 的距离是【 】
(A)等于3cm; (B)大于3cm而小于4cm;
(C)不大于3cm; (D)小于3cm。
C
课堂练习
4、如图,点A、O、E在一条直线上,OB⊥AE,
OC⊥OD,则图中互余的角有 对,
互补的角有 对.
1
2
3
4
O
A
B
C
D
E
4
课堂练习
∠1+∠2=90°
解:互为余角有:
∠1+∠4=90°
∠3+∠2=90°
∠3+∠4=90°
4、如图,点A、O、E在一条直线上,OB⊥AE,
OC⊥OD,则图中互余的角有 对,
互补的角有 对.
1
2
3
4
O
A
B
C
D
E
4
5
课堂练习
∠1+∠COE=180°
解:互为补角有:
∠3+∠COE=180°
∠4+∠AOD=180°
∠2+∠AOD=180°
∠AOB+∠BOE=180°
5、如图,直线AB、EF相交于O,∠DOE=90°, ∠BOC=90°。说出∠AOD的余角、补角; ∠BOE的补角。
∠BOE的补角是:
∠AOE、 ∠COD、∠BOF
∠BOD、 ∠COE
∠AOE 、∠COD、∠BOF
答:∠AOD的余角有:
∠AOD的补角是:
A
O
B
C
D
E
F
6、直线AB、CD相交于O.
⑴OE、OF分别是∠AOC、 ∠BOD的平分线。画出这个图形。
A
B
C
D
O
F
E
⑵ 射线OE、OF在同一条直线上吗?
答: 射线OE、OF在同一条直线上。
6、直线AB、CD相交于O.
⑶ 画∠AOD的平分线OG,OE与OG有什么位置关系?
A
B
C
D
O
F
E
答: OG⊥OE。
G
一、垂线、垂直及表示方法、垂足、垂线段的概念
二、垂线的性质公理:
垂线的画法、点到直线的距离。
归纳与整理
在同一平面内,过一点有且只有一条直线与已知直线垂直。
垂线段最短。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
