5.1.3 同位角、内错角、同旁内角(课件)
文档属性
| 名称 | 5.1.3 同位角、内错角、同旁内角(课件) |

|
|
| 格式 | ppt | ||
| 文件大小 | 5.9MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-02 00:00:00 | ||
图片预览




文档简介
(共41张PPT)
5.1.3 同位角、内错角、
同旁内角
人教版 七年级下
一、复习与巩固
1、我们研究了两条直线相交的情形:
1
2
3
4
⑴ 每一个角都有两个邻补角。
⑵ 每一个角都有一个对顶角。
1、我们研究了两条直线相交的情形:
1
2
3
4
⑶ 两条相交直线形成四对邻补角,
⑷ 两条相交直线形成两对对顶角。
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
四对邻补角
两对对顶角
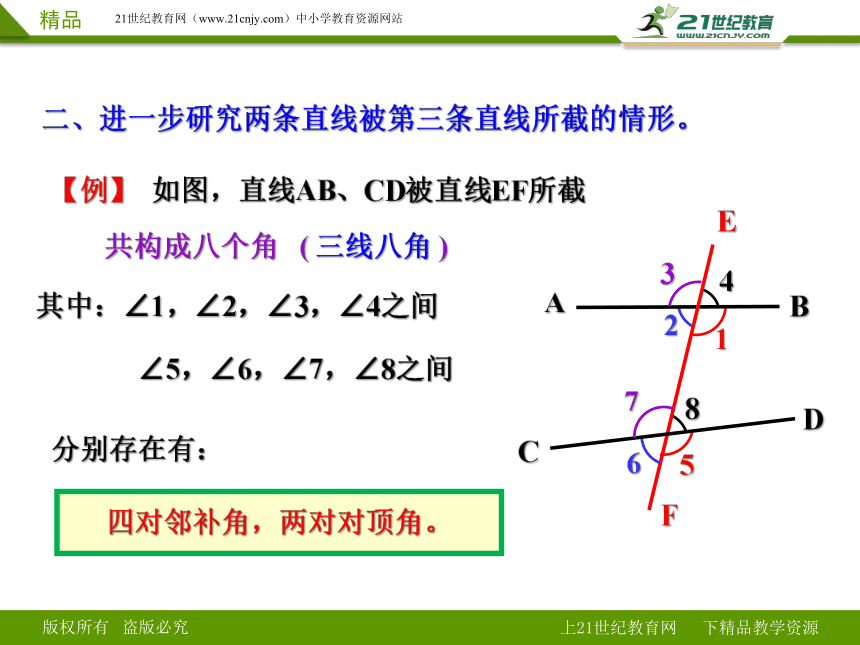
二、进一步研究两条直线被第三条直线所截的情形。
【例】 如图,直线AB、CD被直线EF所截
共构成八个角 ( 三线八角 )
A
B
C
D
E
F
1
5
2
6
3
8
7
4
其中:∠1,∠2,∠3,∠4之间
∠5,∠6,∠7,∠8之间
分别存在有:
四对邻补角,两对对顶角。
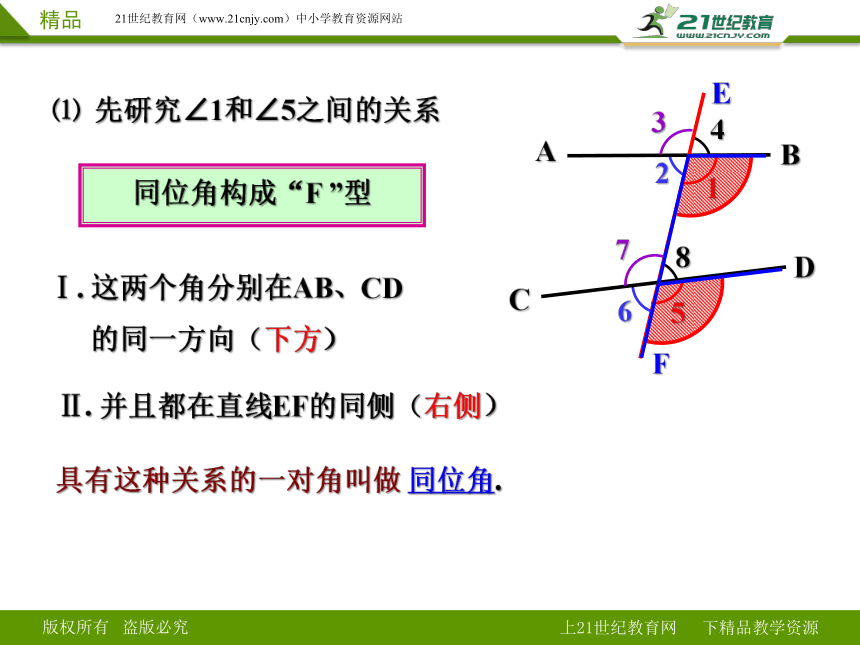
⑴ 先研究∠1和∠5之间的关系
Ⅰ. 这两个角分别在AB、CD
的同一方向(下方)
Ⅱ. 并且都在直线EF的同侧(右侧)
具有这种关系的一对角叫做 同位角.
A
B
C
D
E
F
1
5
2
6
3
8
7
4
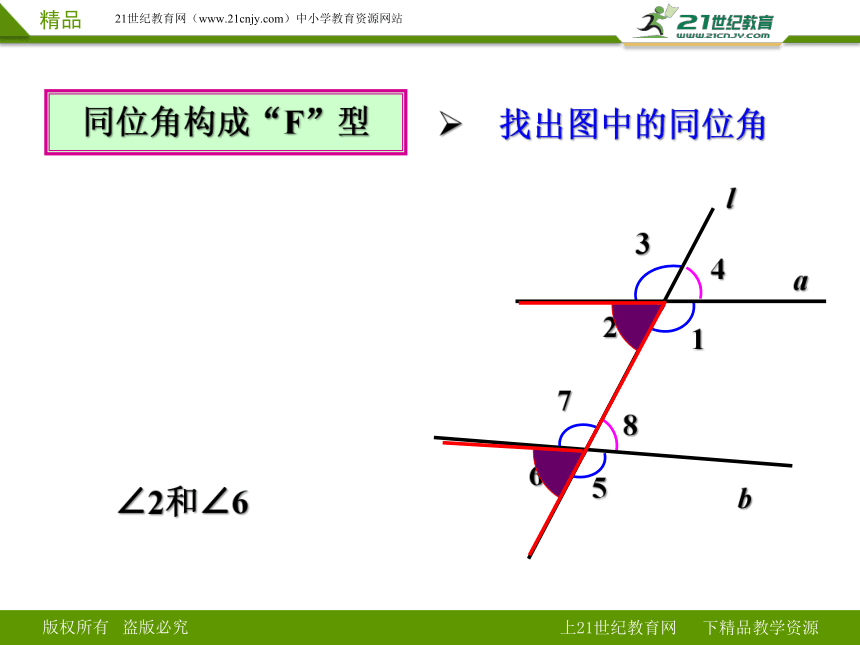
同位角构成“F ”型
3
2
1
4
6
5
8
7
b
a
l
找出图中的同位角
∠2和∠6
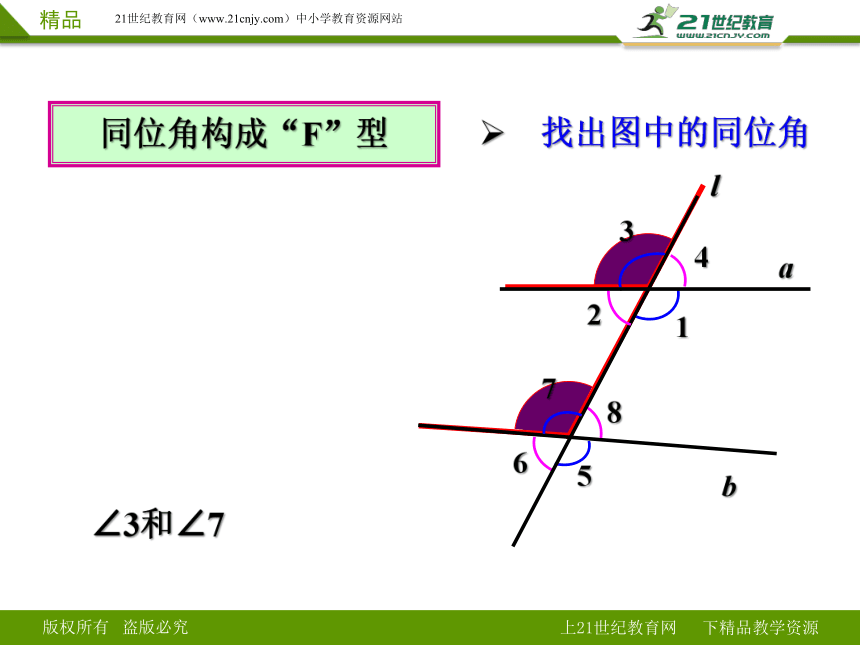
同位角构成“F”型
找出图中的同位角
∠3和∠7
同位角构成“F”型
3
2
1
4
6
5
8
7
b
a
l
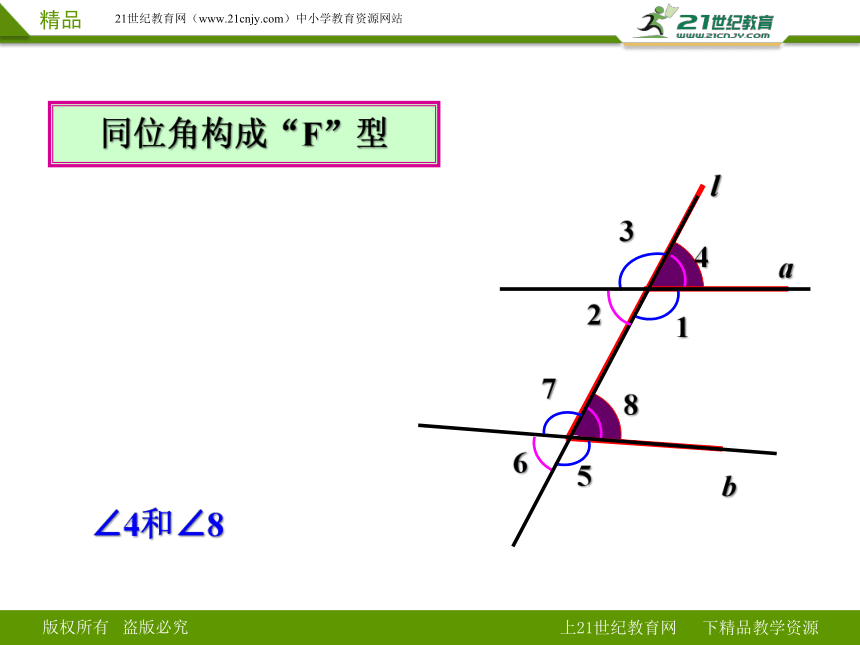
∠4和∠8
同位角构成“F”型
3
2
1
4
6
5
8
7
b
a
l
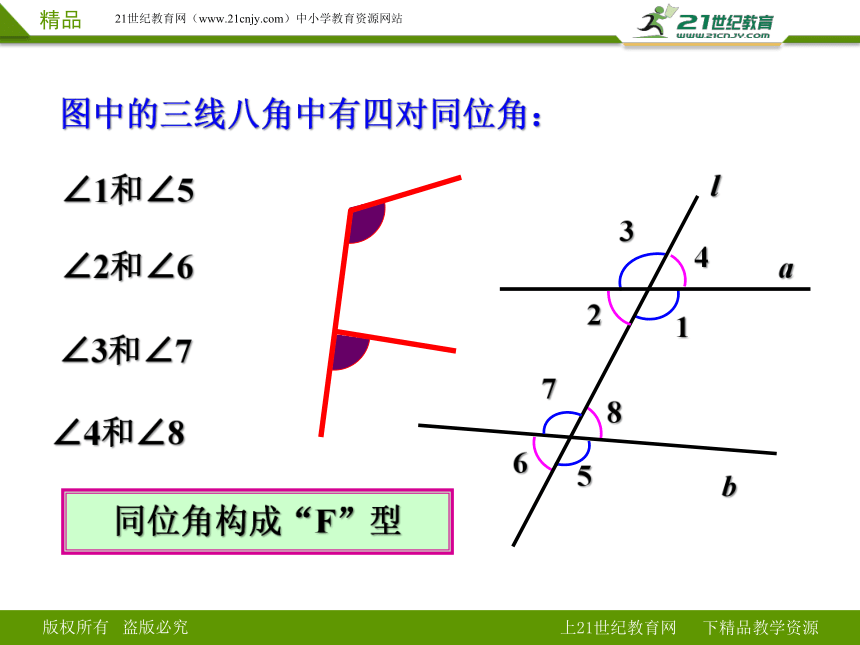
∠1和∠5
图中的三线八角中有四对同位角:
∠2和∠6
∠3和∠7
∠4和∠8
3
2
1
4
6
5
8
7
b
a
l
同位角构成“F”型
⑵ 再研究∠2和∠8的关系
Ⅰ. 这两个角都在AB、CD之间(内部)
Ⅱ. 并且分别在直线EF的两侧(交错位置)
具有这种关系的一对角叫做 内错角.
A
B
C
D
E
F
1
5
2
6
3
8
7
4
内错角构成“Z”字型
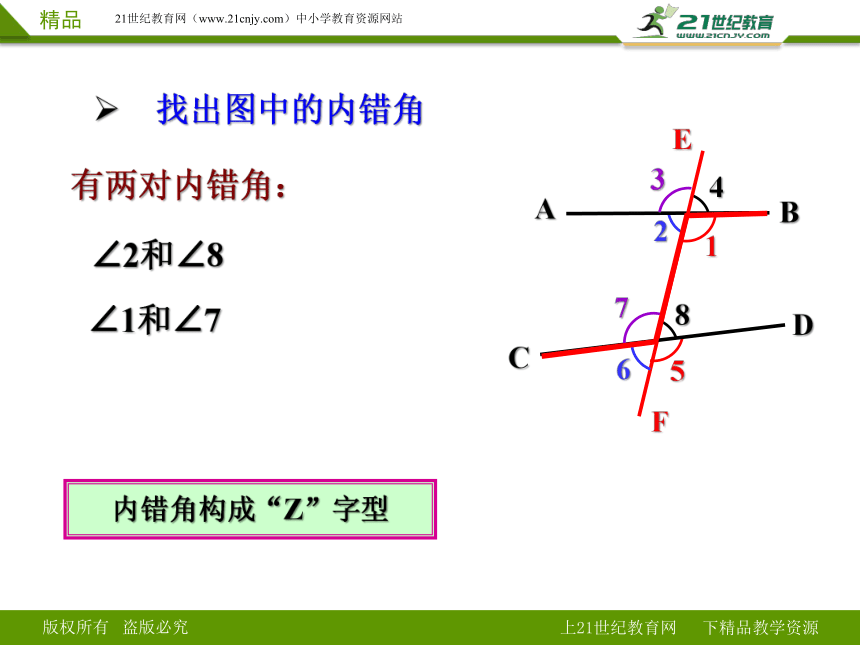
找出图中的内错角
∠2和∠8
有两对内错角:
∠1和∠7
A
B
C
D
E
F
1
5
2
6
3
8
7
4
内错角构成“Z”字型
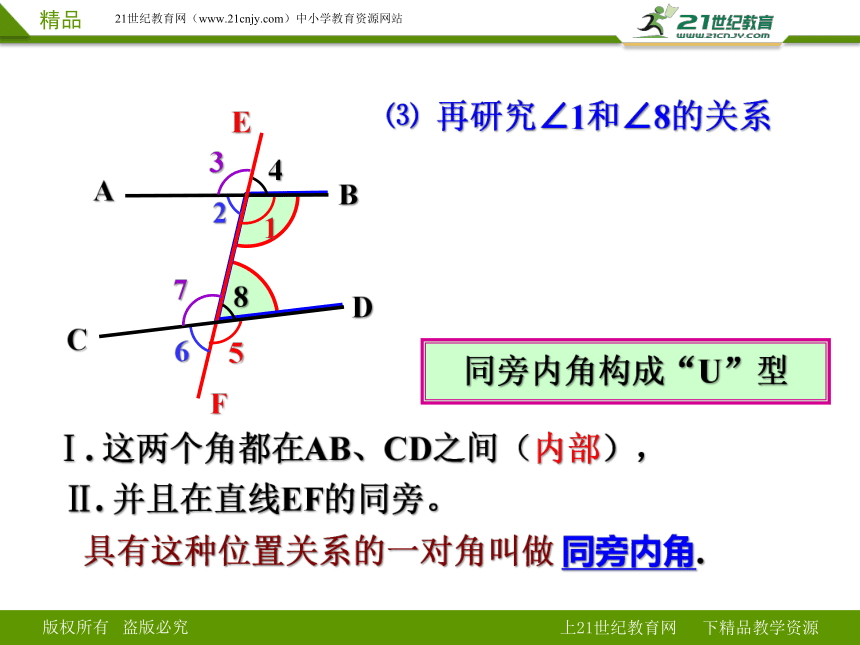
⑶ 再研究∠1和∠8的关系
Ⅰ. 这两个角都在AB、CD之间(内部),
Ⅱ. 并且在直线EF的同旁。
具有这种位置关系的一对角叫做 同旁内角.
同旁内角构成“U”型
A
B
C
D
E
F
1
5
2
6
3
8
7
4
找出图中的同旁内角
∠1和∠8
有两对同旁内角:
∠2和∠7
同旁内角构成“U”型
A
B
C
D
E
F
1
5
2
6
3
8
7
4
如图:直线a、b被直线 l 截的8个角中
四对同位角:
∠1与∠5;∠2与∠6;
∠3与∠7;∠4与∠8.
两对内错角:
∠1与∠7;∠2与∠8.
两对同旁内角:
∠1与∠8 ∠2与∠7
a
b
l
1
5
2
6
3
8
7
4
强化练习
1、与∠1是同位角的是 ,
与∠1是内错角的是 ,
与∠1是同旁内角的是 。
∠5
1
3
2
5
4
∠3
∠2
强化练习
2、 ∠1的同位角的是 ,
∠1的内错角的是 ,
∠1的同旁内角的是 。
1
2
3
4
5
∠3
∠5
∠2
3、如图,∠1与∠2是内错角的是【 】
D
1
2
(A)
1
2
(B)
【注】同位角、内错角、同旁内角必须有公共的边!
(D)
1
2
(C)
1
2
【技巧1】先找两角的公共线!
【技巧2】擦去无关的干扰线!
【技巧3】牢记三类形象的字母!
4、如图,∠1与∠2不是同位角的是【 】
(A)
1
2
(B)
1
2
(C)
1
2
(D)
1
2
C
5、与∠1是同旁内角的是【 】
B
A.∠2 B. ∠2或∠A C.∠3 D.∠4
1
3
2
5
A
B
C
D
E
4
1
2
1
A
6、∠1与∠2是同位角的是【 】
1
2
(A) (B) (C) (D)
1
2
2
1
1
2
【注】同位角、内错角、同旁内角必须有公共的边!
D
7、下列所示的四个图形中,∠1和∠2是同位角的是【 】
1
2
①
1
2
②
1
2
③
1
2
④
A. ②③ B. ①②③ C. ①②④ D. ①④
C
8、已知∠1 +∠2 =180°,则图中
与∠1相等的角是 。
∠8 、∠3、∠5
1
8
2
5
4
6
7
3
A
B
C
D
E
F
1
3
5
2
4
⑴ ∠1与∠2是直线 和 被直线 所
截而得的 角.
BC
AB
DE
同位
9.根据图形,填空 (本题有5个小题)
①画出公共线 (截线).
②找出两条线.
③由符号确定类型.
A
B
C
D
E
F
1
3
5
2
4
⑵∠1与∠3是直线 和 被直线 所
截而得的 角.
BC
DE
AB
内错
9.根据图形,填空 (本题有5个小题)
①画出公共线 (截线).
②找出两条线.
③由符号确定类型.
⑶ ∠3与∠4是直线 __和 _被直线 所
截而得的_______角.
BC
EF
DE
内错
A
B
C
D
E
F
1
3
5
2
4
①画出公共线 (截线).
②找出两条线.
③由符号确定类型.
9.根据图形,填空 (本题有5个小题)
⑷∠2与∠4是直线 和 被直线 所
截而得的 角.
BC
EF
DE
同位
A
B
C
D
E
F
1
3
5
2
4
①画出公共线 (截线).
②找出两条线.
③由符号确定类型.
9.根据图形,填空 (本题有5个小题)
⑸∠4与∠5是直线____和____被直线____ 所
截而得的________角.
DE
BC
A
B
C
D
E
F
1
3
5
2
4
①画出公共线 (截线).
EF
②找出两条线.
同旁内
③由符号确定类型.
9.根据图形,填空 (本题有5个小题)
10、两条直线a、c被第三条直线b所截,若∠α的同旁内角是140°,则∠α的同位角是多少度?
α
a
c
b
解:∠α的同旁内角∠1= 140°
= 180°-∠1
=40°
1
∠α的同位角∠2
2
= 180°- 140°
11、图中的同旁内角共有【 】
A
B
C
D
E
(A).7对 (B).8对 (C).9对 (D).10对
C
∠A和∠ADE
∠A和∠AED
∠ADE和∠AED
∠A和∠B
∠A和∠C
∠B和∠C
∠B和∠BDE
∠BDE和∠DEC
∠DEC和∠C
12、如图,直线DE和BC被第三条直线AB所截, 和
是同位角; 和 是同旁内角。
∠DBC
∠ADE
∠EDB
∠DBC
A
B
C
D
E
A
D
E
B
C
(A).4 (B).3
(C).2 (D).1
13、下列判断:
⑴∠A与∠1是同位角; ⑵∠A与∠B是同旁内角;
⑶∠4与∠1是内错角; ⑷∠1与∠3是同位角。
其中正确的个数是【 】
B
A
B
1
2
3
4
A
B
C
D
E
1
2
14.(本题共3个小题)
⑴∠1与∠C是直线 和 被直线 所
截而成的 角.
AD
BC
EC
同位
⑵∠2与∠B是直线 和 被直线 所
截而成的_________角.
AB
AD
BC
内错
A
B
C
D
E
1
2
⑶∠B与∠C是直线 和 被直线 所
截而成的_________角.
BC
AB
AC
同旁内
A
B
C
D
E
1
2
15、∠EAD与 是同位角;
∠ABC与 是同旁内角;
∠EAD与 是内错角。
∠ABC 或∠ABD
∠C或∠BAD
∠ADC或 ∠ADB
E
A
B
C
D
B
A
C
D
E
3
2
1
16. 找出图中∠B的同位角和同旁内角,图中所有的内错角.
答:⑴∠B的同位角是∠1
⑵ ∠B的同旁内角有:∠3、 ∠A、 ∠BCE
⑶图中的内错角有:
∠2和∠A
∠B的同位角是∠ACD
∠A和∠ACD。
17、试用两种不同的添线方法画出∠B 和∠C 的同位角。
A
B
C
D
E
1
3
2
4
∠ABC的同位角有:
∠1和∠2
∠ACB的同位角有:
∠3和∠4
18、∠B 和∠D 是同旁内角吗?为什么?
你能用直尺画出∠B的同旁内角吗?
A
B
C
D
E
F
G
答:⑴∠B 和∠D 不是同旁内角,因为这两个角没有公共边。
但是∠B 和∠BCD是同旁内角。
1
⑵ 如图画出的∠G 和∠1 都是∠B 的同旁内角。
1、判断三种角的方法
⑴先找“截线”, ⑵再找另外两直线,
⑶根据角的符号位置决定是哪一种角.
2、当图形复杂时可把暂时不需要的线段、角等遮住,也可采用图形分解法、图形涂色法以排除干扰.
小结
主要内容:两条直线被第三条直线所截而产生的
三种角——同位角、内错角、同旁内角.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
5.1.3 同位角、内错角、
同旁内角
人教版 七年级下
一、复习与巩固
1、我们研究了两条直线相交的情形:
1
2
3
4
⑴ 每一个角都有两个邻补角。
⑵ 每一个角都有一个对顶角。
1、我们研究了两条直线相交的情形:
1
2
3
4
⑶ 两条相交直线形成四对邻补角,
⑷ 两条相交直线形成两对对顶角。
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
四对邻补角
两对对顶角
二、进一步研究两条直线被第三条直线所截的情形。
【例】 如图,直线AB、CD被直线EF所截
共构成八个角 ( 三线八角 )
A
B
C
D
E
F
1
5
2
6
3
8
7
4
其中:∠1,∠2,∠3,∠4之间
∠5,∠6,∠7,∠8之间
分别存在有:
四对邻补角,两对对顶角。
⑴ 先研究∠1和∠5之间的关系
Ⅰ. 这两个角分别在AB、CD
的同一方向(下方)
Ⅱ. 并且都在直线EF的同侧(右侧)
具有这种关系的一对角叫做 同位角.
A
B
C
D
E
F
1
5
2
6
3
8
7
4
同位角构成“F ”型
3
2
1
4
6
5
8
7
b
a
l
找出图中的同位角
∠2和∠6
同位角构成“F”型
找出图中的同位角
∠3和∠7
同位角构成“F”型
3
2
1
4
6
5
8
7
b
a
l
∠4和∠8
同位角构成“F”型
3
2
1
4
6
5
8
7
b
a
l
∠1和∠5
图中的三线八角中有四对同位角:
∠2和∠6
∠3和∠7
∠4和∠8
3
2
1
4
6
5
8
7
b
a
l
同位角构成“F”型
⑵ 再研究∠2和∠8的关系
Ⅰ. 这两个角都在AB、CD之间(内部)
Ⅱ. 并且分别在直线EF的两侧(交错位置)
具有这种关系的一对角叫做 内错角.
A
B
C
D
E
F
1
5
2
6
3
8
7
4
内错角构成“Z”字型
找出图中的内错角
∠2和∠8
有两对内错角:
∠1和∠7
A
B
C
D
E
F
1
5
2
6
3
8
7
4
内错角构成“Z”字型
⑶ 再研究∠1和∠8的关系
Ⅰ. 这两个角都在AB、CD之间(内部),
Ⅱ. 并且在直线EF的同旁。
具有这种位置关系的一对角叫做 同旁内角.
同旁内角构成“U”型
A
B
C
D
E
F
1
5
2
6
3
8
7
4
找出图中的同旁内角
∠1和∠8
有两对同旁内角:
∠2和∠7
同旁内角构成“U”型
A
B
C
D
E
F
1
5
2
6
3
8
7
4
如图:直线a、b被直线 l 截的8个角中
四对同位角:
∠1与∠5;∠2与∠6;
∠3与∠7;∠4与∠8.
两对内错角:
∠1与∠7;∠2与∠8.
两对同旁内角:
∠1与∠8 ∠2与∠7
a
b
l
1
5
2
6
3
8
7
4
强化练习
1、与∠1是同位角的是 ,
与∠1是内错角的是 ,
与∠1是同旁内角的是 。
∠5
1
3
2
5
4
∠3
∠2
强化练习
2、 ∠1的同位角的是 ,
∠1的内错角的是 ,
∠1的同旁内角的是 。
1
2
3
4
5
∠3
∠5
∠2
3、如图,∠1与∠2是内错角的是【 】
D
1
2
(A)
1
2
(B)
【注】同位角、内错角、同旁内角必须有公共的边!
(D)
1
2
(C)
1
2
【技巧1】先找两角的公共线!
【技巧2】擦去无关的干扰线!
【技巧3】牢记三类形象的字母!
4、如图,∠1与∠2不是同位角的是【 】
(A)
1
2
(B)
1
2
(C)
1
2
(D)
1
2
C
5、与∠1是同旁内角的是【 】
B
A.∠2 B. ∠2或∠A C.∠3 D.∠4
1
3
2
5
A
B
C
D
E
4
1
2
1
A
6、∠1与∠2是同位角的是【 】
1
2
(A) (B) (C) (D)
1
2
2
1
1
2
【注】同位角、内错角、同旁内角必须有公共的边!
D
7、下列所示的四个图形中,∠1和∠2是同位角的是【 】
1
2
①
1
2
②
1
2
③
1
2
④
A. ②③ B. ①②③ C. ①②④ D. ①④
C
8、已知∠1 +∠2 =180°,则图中
与∠1相等的角是 。
∠8 、∠3、∠5
1
8
2
5
4
6
7
3
A
B
C
D
E
F
1
3
5
2
4
⑴ ∠1与∠2是直线 和 被直线 所
截而得的 角.
BC
AB
DE
同位
9.根据图形,填空 (本题有5个小题)
①画出公共线 (截线).
②找出两条线.
③由符号确定类型.
A
B
C
D
E
F
1
3
5
2
4
⑵∠1与∠3是直线 和 被直线 所
截而得的 角.
BC
DE
AB
内错
9.根据图形,填空 (本题有5个小题)
①画出公共线 (截线).
②找出两条线.
③由符号确定类型.
⑶ ∠3与∠4是直线 __和 _被直线 所
截而得的_______角.
BC
EF
DE
内错
A
B
C
D
E
F
1
3
5
2
4
①画出公共线 (截线).
②找出两条线.
③由符号确定类型.
9.根据图形,填空 (本题有5个小题)
⑷∠2与∠4是直线 和 被直线 所
截而得的 角.
BC
EF
DE
同位
A
B
C
D
E
F
1
3
5
2
4
①画出公共线 (截线).
②找出两条线.
③由符号确定类型.
9.根据图形,填空 (本题有5个小题)
⑸∠4与∠5是直线____和____被直线____ 所
截而得的________角.
DE
BC
A
B
C
D
E
F
1
3
5
2
4
①画出公共线 (截线).
EF
②找出两条线.
同旁内
③由符号确定类型.
9.根据图形,填空 (本题有5个小题)
10、两条直线a、c被第三条直线b所截,若∠α的同旁内角是140°,则∠α的同位角是多少度?
α
a
c
b
解:∠α的同旁内角∠1= 140°
= 180°-∠1
=40°
1
∠α的同位角∠2
2
= 180°- 140°
11、图中的同旁内角共有【 】
A
B
C
D
E
(A).7对 (B).8对 (C).9对 (D).10对
C
∠A和∠ADE
∠A和∠AED
∠ADE和∠AED
∠A和∠B
∠A和∠C
∠B和∠C
∠B和∠BDE
∠BDE和∠DEC
∠DEC和∠C
12、如图,直线DE和BC被第三条直线AB所截, 和
是同位角; 和 是同旁内角。
∠DBC
∠ADE
∠EDB
∠DBC
A
B
C
D
E
A
D
E
B
C
(A).4 (B).3
(C).2 (D).1
13、下列判断:
⑴∠A与∠1是同位角; ⑵∠A与∠B是同旁内角;
⑶∠4与∠1是内错角; ⑷∠1与∠3是同位角。
其中正确的个数是【 】
B
A
B
1
2
3
4
A
B
C
D
E
1
2
14.(本题共3个小题)
⑴∠1与∠C是直线 和 被直线 所
截而成的 角.
AD
BC
EC
同位
⑵∠2与∠B是直线 和 被直线 所
截而成的_________角.
AB
AD
BC
内错
A
B
C
D
E
1
2
⑶∠B与∠C是直线 和 被直线 所
截而成的_________角.
BC
AB
AC
同旁内
A
B
C
D
E
1
2
15、∠EAD与 是同位角;
∠ABC与 是同旁内角;
∠EAD与 是内错角。
∠ABC 或∠ABD
∠C或∠BAD
∠ADC或 ∠ADB
E
A
B
C
D
B
A
C
D
E
3
2
1
16. 找出图中∠B的同位角和同旁内角,图中所有的内错角.
答:⑴∠B的同位角是∠1
⑵ ∠B的同旁内角有:∠3、 ∠A、 ∠BCE
⑶图中的内错角有:
∠2和∠A
∠B的同位角是∠ACD
∠A和∠ACD。
17、试用两种不同的添线方法画出∠B 和∠C 的同位角。
A
B
C
D
E
1
3
2
4
∠ABC的同位角有:
∠1和∠2
∠ACB的同位角有:
∠3和∠4
18、∠B 和∠D 是同旁内角吗?为什么?
你能用直尺画出∠B的同旁内角吗?
A
B
C
D
E
F
G
答:⑴∠B 和∠D 不是同旁内角,因为这两个角没有公共边。
但是∠B 和∠BCD是同旁内角。
1
⑵ 如图画出的∠G 和∠1 都是∠B 的同旁内角。
1、判断三种角的方法
⑴先找“截线”, ⑵再找另外两直线,
⑶根据角的符号位置决定是哪一种角.
2、当图形复杂时可把暂时不需要的线段、角等遮住,也可采用图形分解法、图形涂色法以排除干扰.
小结
主要内容:两条直线被第三条直线所截而产生的
三种角——同位角、内错角、同旁内角.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
