5.3.1 平行线的性质(课件)
图片预览





文档简介
(共24张PPT)
5.3.1 平行线的性质
人教版 七年级下
一、引言
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行。
反过来,如果两条直线平行,同位角、内错角、同旁内角又各有什么关系呢?
这就是我们下面要学行线的性质。
类似于研究平行线的判定,我们先来研究两条直线平行时,它们被第三条直线截得的同位角的关系。
二、实验操作
⑴ 请你在画好的平行线上任意画一条截线
A
B
C
D
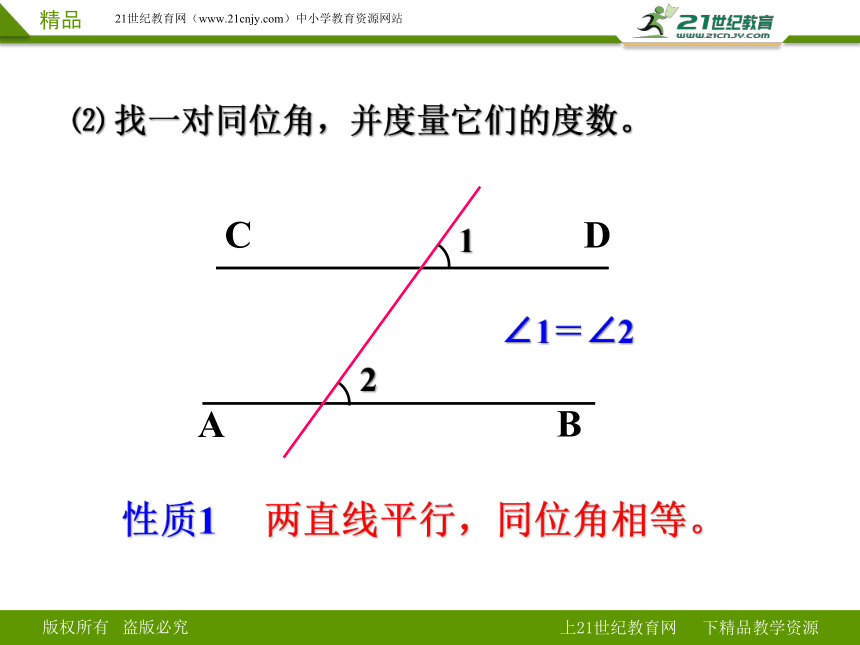
⑵ 找一对同位角,并度量它们的度数。
∠1=∠2
性质1 两直线平行,同位角相等。
1
2
A
B
C
D
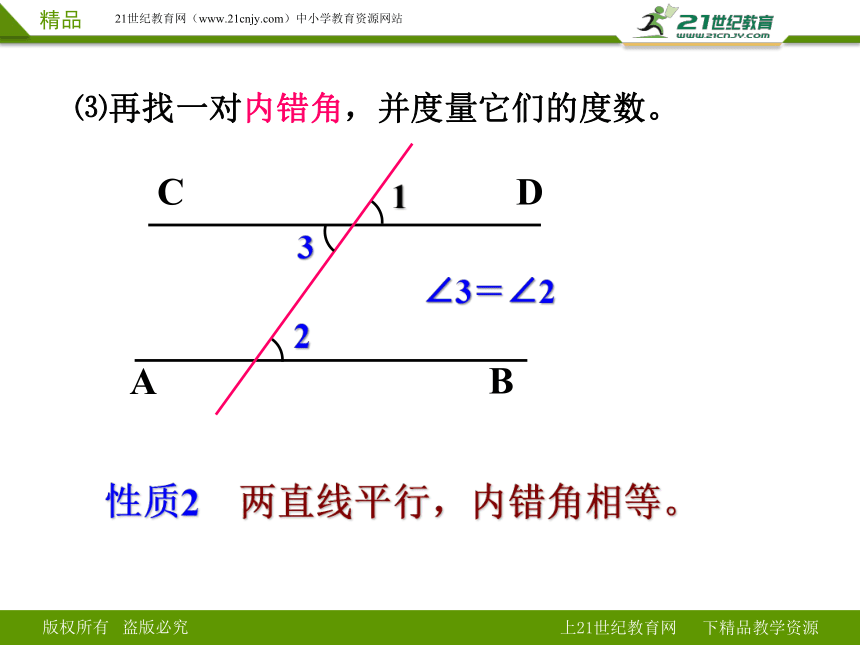
⑶再找一对内错角,并度量它们的度数。
性质2 两直线平行,内错角相等。
1
2
3
∠3=∠2
2
A
B
C
D
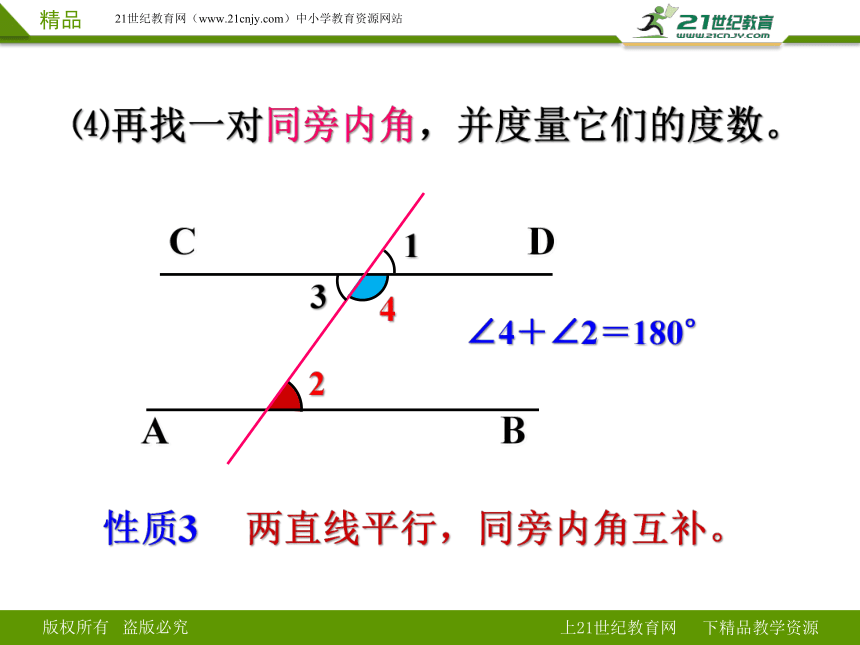
⑷再找一对同旁内角,并度量它们的度数。
性质3 两直线平行,同旁内角互补。
1
3
4
∠4+∠2=180°
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
平行线的性质
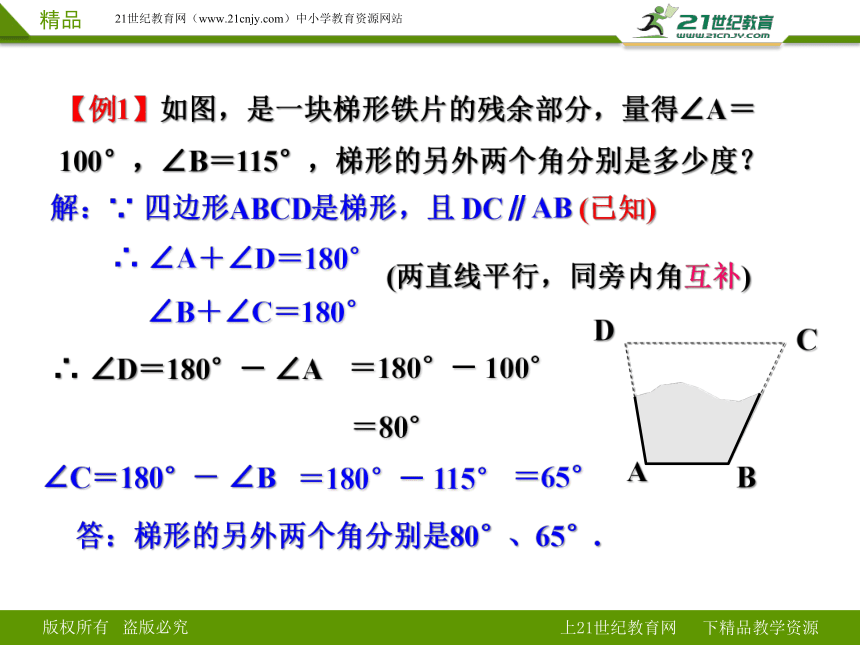
【例1】如图,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
A
B
C
D
解:∵ 四边形ABCD是梯形,且 DC∥AB (已知)
∴ ∠A+∠D=180°
∠B+∠C=180°
(两直线平行,同旁内角互补)
∴ ∠D=180°- ∠A
=180°- 100°
=80°
∠C=180°- ∠B
=180°- 115°
=65°
答:梯形的另外两个角分别是80°、65°.
课堂练习
1、如图,直线a∥b,∠1=54°,
求∠2,∠3,∠4的度数。
解:⑴ ∵∠2=∠1 (对顶角相等)
∠1=54°( 已知 )
1
2
3
4
a
b
∴∠2=54° (等量代换)
⑵ ∵ a∥b (已知)
∴∠2+∠3=180°
∴∠3=180°-∠2
=180°-54°
=126°
1、如图,直线a∥b,∠1=54°,
求∠2,∠3,∠4的度数。
1
2
3
4
a
b
(两直线平行同旁内角互补)
⑶ ∵ a∥b (已知)
∴∠4=∠1=54°
1、如图,直线a∥b,∠1=54°,
求∠2,∠3,∠4的度数。
1
2
3
4
a
b
(两直线平行同位角相等)
2、如图,△ABC中,D是AB上一点, E是AC上一点, ∠ADE=60°,∠B=60°,∠AED=40°。
⑴ DE和BC平行吗?为什么?
⑵ ∠C是多少度?为什么?
A
B
C
D
E
解:⑴ DE∥BC,理由如下:
∵∠ADE=60°,∠B=60° (已知)
∴ ∠ADE=∠B (等量代换)
∴ DE∥BC (同位角相等,两直线平行)
2、如图,△ABC中,D是AB上一点, E是AC上一点, ∠ADE=60°,∠B=60°,∠AED=40°。
⑴ DE和BC平行吗?为什么?
⑵ ∠C是多少度?为什么?
⑵ 由⑴知 DE∥BC
∵∠AED=60° (已知)
∴ ∠C=∠AED (两直线平行,同位角相等)
∴ ∠C=60° (等量代换)
A
B
C
D
E
3、如图a∥b,∠1=108°,则∠2的度数是【 】
A. 72° B.80° C.82° D.108°
1
2
a
b
A
3
∠3=180°-∠1
=180°-108°
=72°
∴∠2=∠3=72°
4. 如图,由AB∥CD,可以得到【 】
(A) ∠1=∠2 (B) ∠2=∠3
(C) ∠1=∠4 (D) ∠3=∠4
A
B
C
D
1
2
3
4
C
5、将一直角三角板与两边平行的纸条如图所示放置,
则下列结论:①∠1=∠2; ②∠3=∠4;
③∠2+∠4=90°;④∠4+∠5=180°。
其中正确结论的个数为【 】
A.1 B.2 C.3 D.4
1
4
3
2
5
D
6、如图,AB∥CD,直线HE⊥MN交MN于E,
∠1=130°,则∠2等于【 】
A.50° B.40° C.30° D.60°
A
B
C
D
M
N
E
H
F
1
2
B
∵AB∥CD
∠EFC=∠1=130°
∴∠AEM=∠EFC=130°
∴∠2=130°-90°
=40°
7、如图,如果AB∥CD,则角α、β、γ 之间的
关系式为【 】
A.α+β+γ=360 B.α-β+γ=180
C.α+β+γ=180 D.α+β-γ=180
A
B
C
D
E
α
β
γ
D
A
B
C
D
E
F
8、★如图,已知AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠EDC的关系是【 】
A. ∠ABE=3∠D
B.∠ABE+∠D=180°
C. ∠ABE-∠D=90°
D.∠ABE=2∠D
D
G
9、如图a∥b,∠ABC=120°,a ⊥AB
则∠1的 度数是 .
30°
1
a
A
b
B
C
120°
10、有一条直的等宽的纸带,按如图折叠,纸带重叠
部分中的∠α度数为 。
A
B
C
30°
D
75°
同位角相等,两直线平行。
判定方法1
判定方法2
内错角相等,两直线平行。
判定方法3
同旁内角互补,两直线平行。
两直线平行,同位角相等。
性质1
性质2
两直线平行,内错角相等。
性质3
两直线平行,同旁内角互补。
5.3.1 平行线的性质
人教版 七年级下
一、引言
利用同位角相等,或者内错角相等,或者同旁内角互补,可以判定两条直线平行。
反过来,如果两条直线平行,同位角、内错角、同旁内角又各有什么关系呢?
这就是我们下面要学行线的性质。
类似于研究平行线的判定,我们先来研究两条直线平行时,它们被第三条直线截得的同位角的关系。
二、实验操作
⑴ 请你在画好的平行线上任意画一条截线
A
B
C
D
⑵ 找一对同位角,并度量它们的度数。
∠1=∠2
性质1 两直线平行,同位角相等。
1
2
A
B
C
D
⑶再找一对内错角,并度量它们的度数。
性质2 两直线平行,内错角相等。
1
2
3
∠3=∠2
2
A
B
C
D
⑷再找一对同旁内角,并度量它们的度数。
性质3 两直线平行,同旁内角互补。
1
3
4
∠4+∠2=180°
两直线平行,同位角相等。
两直线平行,内错角相等。
两直线平行,同旁内角互补。
平行线的性质
【例1】如图,是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角分别是多少度?
A
B
C
D
解:∵ 四边形ABCD是梯形,且 DC∥AB (已知)
∴ ∠A+∠D=180°
∠B+∠C=180°
(两直线平行,同旁内角互补)
∴ ∠D=180°- ∠A
=180°- 100°
=80°
∠C=180°- ∠B
=180°- 115°
=65°
答:梯形的另外两个角分别是80°、65°.
课堂练习
1、如图,直线a∥b,∠1=54°,
求∠2,∠3,∠4的度数。
解:⑴ ∵∠2=∠1 (对顶角相等)
∠1=54°( 已知 )
1
2
3
4
a
b
∴∠2=54° (等量代换)
⑵ ∵ a∥b (已知)
∴∠2+∠3=180°
∴∠3=180°-∠2
=180°-54°
=126°
1、如图,直线a∥b,∠1=54°,
求∠2,∠3,∠4的度数。
1
2
3
4
a
b
(两直线平行同旁内角互补)
⑶ ∵ a∥b (已知)
∴∠4=∠1=54°
1、如图,直线a∥b,∠1=54°,
求∠2,∠3,∠4的度数。
1
2
3
4
a
b
(两直线平行同位角相等)
2、如图,△ABC中,D是AB上一点, E是AC上一点, ∠ADE=60°,∠B=60°,∠AED=40°。
⑴ DE和BC平行吗?为什么?
⑵ ∠C是多少度?为什么?
A
B
C
D
E
解:⑴ DE∥BC,理由如下:
∵∠ADE=60°,∠B=60° (已知)
∴ ∠ADE=∠B (等量代换)
∴ DE∥BC (同位角相等,两直线平行)
2、如图,△ABC中,D是AB上一点, E是AC上一点, ∠ADE=60°,∠B=60°,∠AED=40°。
⑴ DE和BC平行吗?为什么?
⑵ ∠C是多少度?为什么?
⑵ 由⑴知 DE∥BC
∵∠AED=60° (已知)
∴ ∠C=∠AED (两直线平行,同位角相等)
∴ ∠C=60° (等量代换)
A
B
C
D
E
3、如图a∥b,∠1=108°,则∠2的度数是【 】
A. 72° B.80° C.82° D.108°
1
2
a
b
A
3
∠3=180°-∠1
=180°-108°
=72°
∴∠2=∠3=72°
4. 如图,由AB∥CD,可以得到【 】
(A) ∠1=∠2 (B) ∠2=∠3
(C) ∠1=∠4 (D) ∠3=∠4
A
B
C
D
1
2
3
4
C
5、将一直角三角板与两边平行的纸条如图所示放置,
则下列结论:①∠1=∠2; ②∠3=∠4;
③∠2+∠4=90°;④∠4+∠5=180°。
其中正确结论的个数为【 】
A.1 B.2 C.3 D.4
1
4
3
2
5
D
6、如图,AB∥CD,直线HE⊥MN交MN于E,
∠1=130°,则∠2等于【 】
A.50° B.40° C.30° D.60°
A
B
C
D
M
N
E
H
F
1
2
B
∵AB∥CD
∠EFC=∠1=130°
∴∠AEM=∠EFC=130°
∴∠2=130°-90°
=40°
7、如图,如果AB∥CD,则角α、β、γ 之间的
关系式为【 】
A.α+β+γ=360 B.α-β+γ=180
C.α+β+γ=180 D.α+β-γ=180
A
B
C
D
E
α
β
γ
D
A
B
C
D
E
F
8、★如图,已知AB∥CD,BF平分∠ABE,且BF∥DE,则∠ABE与∠EDC的关系是【 】
A. ∠ABE=3∠D
B.∠ABE+∠D=180°
C. ∠ABE-∠D=90°
D.∠ABE=2∠D
D
G
9、如图a∥b,∠ABC=120°,a ⊥AB
则∠1的 度数是 .
30°
1
a
A
b
B
C
120°
10、有一条直的等宽的纸带,按如图折叠,纸带重叠
部分中的∠α度数为 。
A
B
C
30°
D
75°
同位角相等,两直线平行。
判定方法1
判定方法2
内错角相等,两直线平行。
判定方法3
同旁内角互补,两直线平行。
两直线平行,同位角相等。
性质1
性质2
两直线平行,内错角相等。
性质3
两直线平行,同旁内角互补。
