5.4 平移(课件)
图片预览



文档简介
(共25张PPT)
5.4 平移
人教版 七年级下
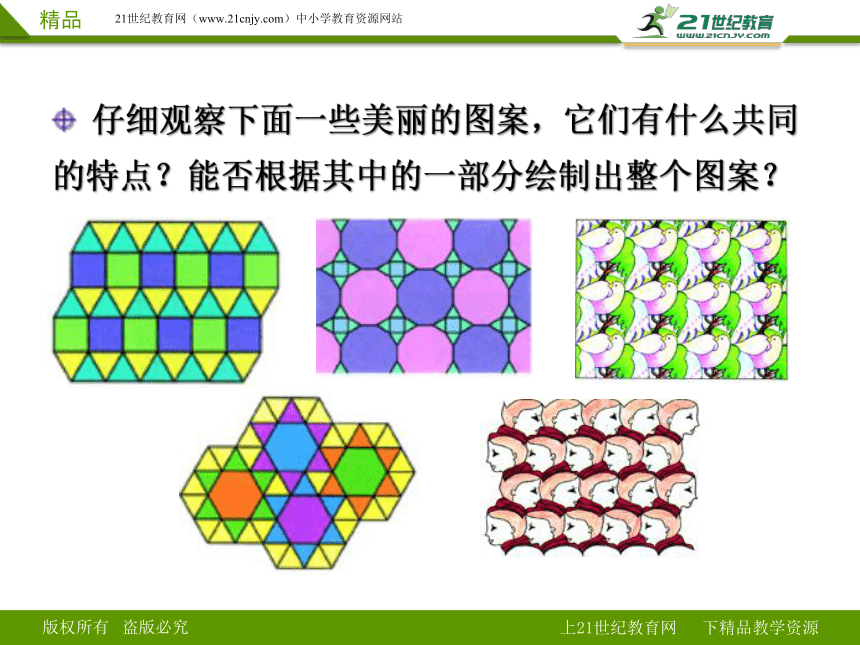
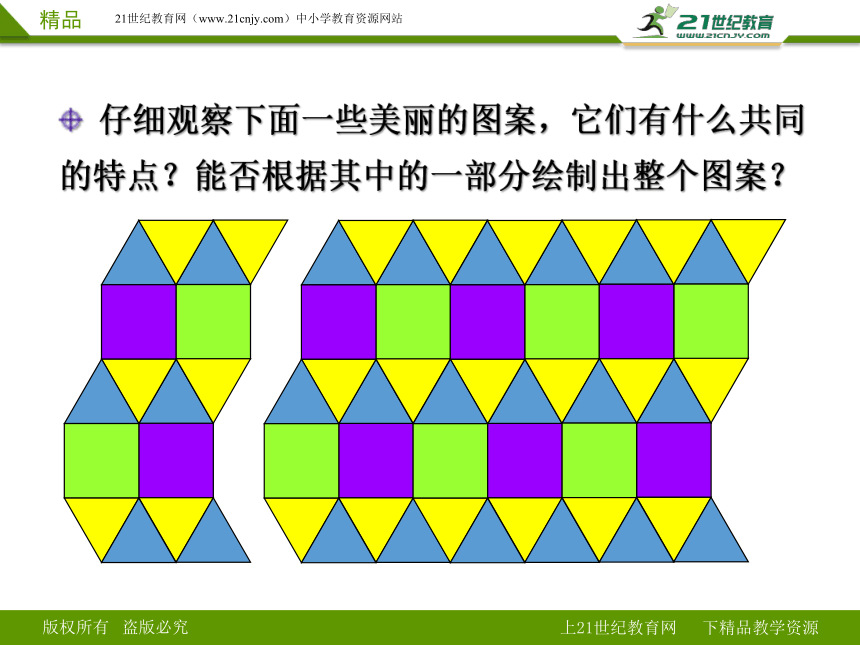
仔细观察下面一些美丽的图案,它们有什么共同的特点?能否根据其中的一部分绘制出整个图案?
仔细观察下面一些美丽的图案,它们有什么共同的特点?能否根据其中的一部分绘制出整个图案?
探究
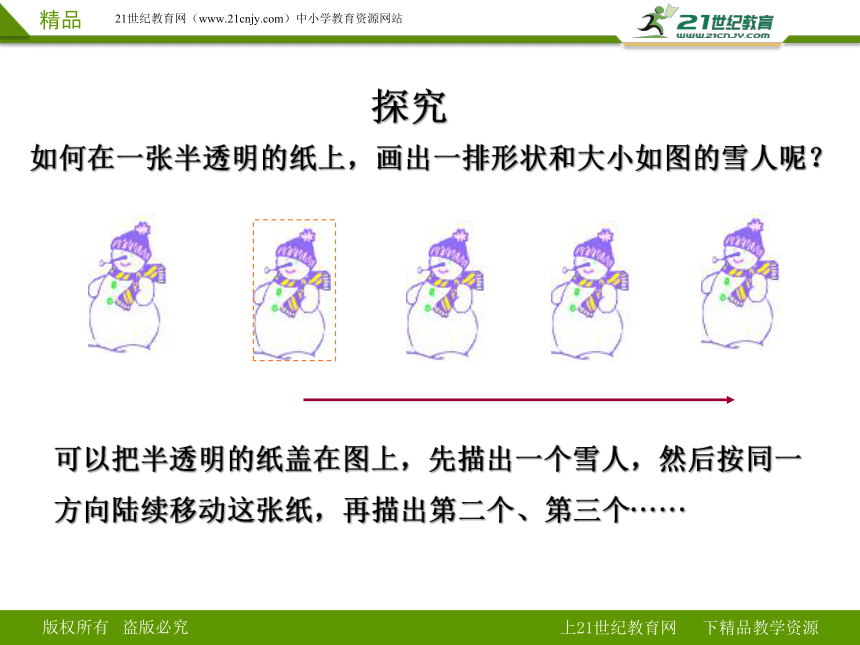
如何在一张半透明的纸上,画出一排形状和大小如图的雪人呢?
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个······
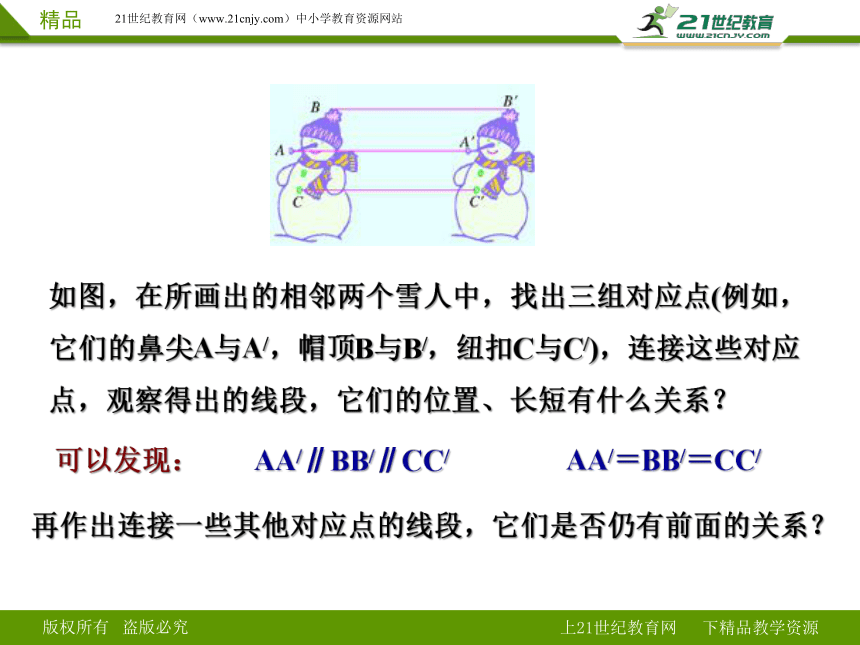
如图,在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A/,帽顶B与B/,纽扣C与C/),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
可以发现:
AA/∥BB/∥CC/
AA/=BB/=CC/
再作出连接一些其他对应点的线段,它们是否仍有前面的关系?
归纳
1、把一个图形整体沿某一直线方向移动,会得到一个新图形,新图形与原图形的形状和大小完全相同。
2、新图形中的每一点,都是原图形中的某一点移动后得到的,这两个点是对应点,连接对应点的线段平行(或在同一条直线上)且相等。
图形的这种移动叫做平移。
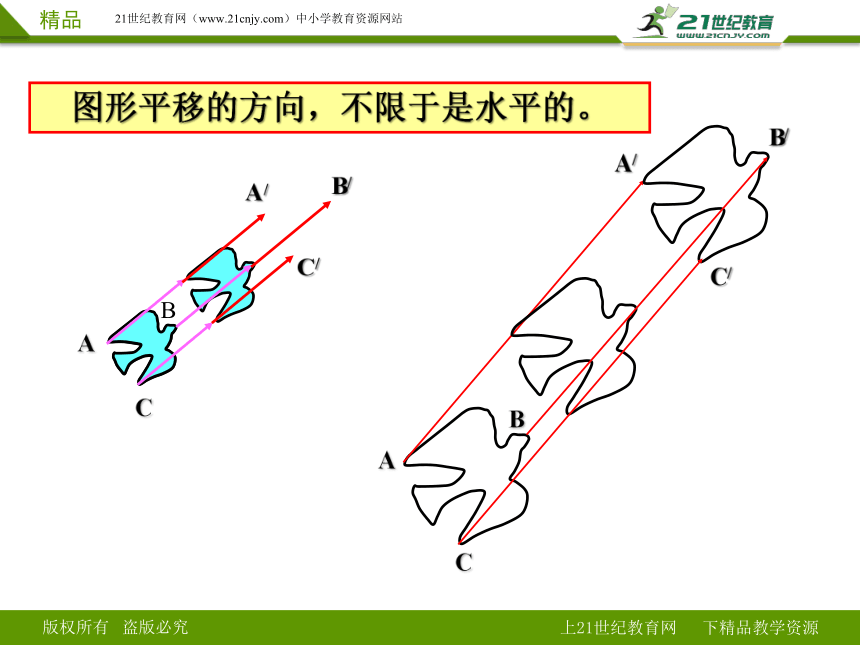
图形平移的方向,不限于是水平的。
A
B
C
A/
B/
C/
A
B
C
A/
B/
C/
平移在我们的生活中是很常见的,利用平移也可以制作很多美丽的图案,你能举出生活中一些利用平移的例子吗?
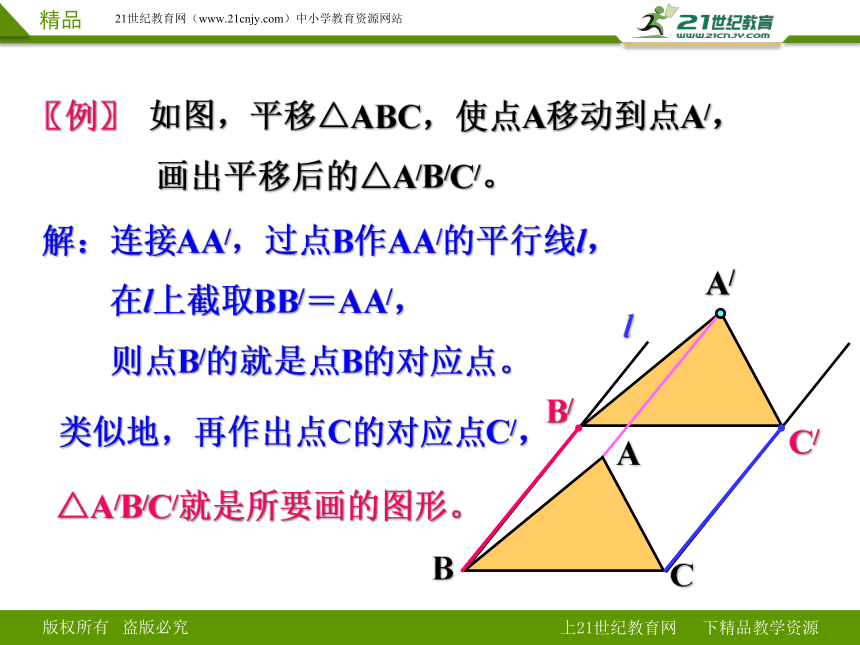
〖例〗 如图,平移△ABC,使点A移动到点A/,
画出平移后的△A/B/C/。
A
B
C
A/
解:连接AA/,过点B作AA/的平行线l,
在l上截取BB/=AA/,
则点B/的就是点B的对应点。
l
B/
类似地,再作出点C的对应点C/,
C/
△A/B/C/就是所要画的图形。
1、如图,△DEF是△ABC经过平移得到的,
则平移的距离是线段 的长度。
A
B
C
D
E
F
BE或CF
课堂练习
2、一个图形经过平移变换后,有以下几种说法,
其中不正确的说法是【 】
(A). 平移后图形的形状和大小都不改变;
(B).平移后的图形与原图形的对应线段平行
(或在同一条直线上)且相等,对应角相等。
(C). 平移后的图形形状不变,但大小可以改变;
(D). 利用基本图形的平移可以设计美丽的图案。
C
3、将长度为10cm的线段向上平移5cm,所得线段
的长度是【 】
A
(A). 10cm (B). 5cm (C). 0 (D). 无法确定。
10cm
10cm
5cm
5cm
4、如图,若△ABC可以看作由△DEF经过平移得到的,已知AB=3,BE=2,则BD等于【 】
(A). 1 (B). 2 (C). 3 (D). 5。
A
B
C
D
E
F
A
5、如图,它是由四个大小、形状完全一样的小三角形组成的,下列不可能实现的情况是【 】
(A). △ADE由△DBF平移得到;
(B).平移△BDF可以得到△FEC;
(C). 平移△EFC可以得到△ADE ;
(D). 通过平移△FEC可以得到△DEF。
D
A
B
C
D
E
F
6、如图, △ABC平移△DEF的位置,有下列结论:⑴ AD=BE=CF,AD∥BE∥CF
⑵ AB∥DE,BC∥EF,AC∥DF
⑶ AB=DE,BC=EF,AC=DF
其中正确的有【 】个
(A). 0; (B). 1; (C). 2; (D). 3。
D
A
B
C
D
E
F
7、如图, 面积为12cm2的△ABC沿BC方向平移到△DEF的位置,平移的距离是边BC长的2倍,则图中四边形ACFD的面积为【 】
(A). 24cm2;
(B). 36cm2;
(C). 48cm2;
(D). 无法确定。
C
A
B
C
D
E
F
G
8、如图,在一块长为am,宽为bm的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1m,就是它的右边线,求这块草地的绿地面积。
a
b
解:(a-1)b
中考链接
1、如图,△DEF是△ABC经过平移得到的,已知∠A=54°,∠ABC=36°,则下列结论不一定成立的是【 】
A
B
C
D
E
F
(A). ∠F=90°
(B). ∠BED=∠FED
(C). BC⊥DF
(D). DF∥AC
B
2、将△ABE的边AE沿所在的直线向右平移4cm,得到梯形ABCD,若△ABE的周长为11cm,则梯形ABCD的周长 。
19cm
A
B
C
D
E
4cm
4cm
3、如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分的面积。
8
24
A
B
C
D
E
F
W
G
H
6
解:由平移可知
S梯形ABCD=S梯形EFGH
∴ S阴影=S梯形DWGH
∵ CW=6cm
∴ DW=24-6=18(cm)
3、如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分的面积。
8
24
A
B
C
D
E
F
W
G
H
6
∵ CW=6cm
∴ DW=24-6=18(cm)
∴ S阴影=(DW+HG)×WG÷2
=(18+24)×8÷2
=168(cm2)
4、如图,⑴ 在3×3网格中,每一个小正方形的边长都是1,△ABC是网格中的等腰三角形,平移△ABC,要求平移后的△ABC各顶点必须在网格的交点上,共可以得到几个这样的三角形(包括△ABC)?
A
B
C
解:在3×3网格中
平移共可得到:4个等腰三角形
4=22
4、如图,⑵在4×4网格中,每一个小正方形的边长都是1,△ABC是网格中的等腰三角形,平移△ABC,要求平移后的△ABC各顶点必须在网格的交点上,共可以得到几个这样的三角形(包括△ABC)?
B
C
解:在4×4网格中
平移共可得到:9个等腰三角形
9=32
A
在5×5网格中
平移共可得到:16个等腰三角形
16=42
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
5.4 平移
人教版 七年级下
仔细观察下面一些美丽的图案,它们有什么共同的特点?能否根据其中的一部分绘制出整个图案?
仔细观察下面一些美丽的图案,它们有什么共同的特点?能否根据其中的一部分绘制出整个图案?
探究
如何在一张半透明的纸上,画出一排形状和大小如图的雪人呢?
可以把半透明的纸盖在图上,先描出一个雪人,然后按同一方向陆续移动这张纸,再描出第二个、第三个······
如图,在所画出的相邻两个雪人中,找出三组对应点(例如,它们的鼻尖A与A/,帽顶B与B/,纽扣C与C/),连接这些对应点,观察得出的线段,它们的位置、长短有什么关系?
可以发现:
AA/∥BB/∥CC/
AA/=BB/=CC/
再作出连接一些其他对应点的线段,它们是否仍有前面的关系?
归纳
1、把一个图形整体沿某一直线方向移动,会得到一个新图形,新图形与原图形的形状和大小完全相同。
2、新图形中的每一点,都是原图形中的某一点移动后得到的,这两个点是对应点,连接对应点的线段平行(或在同一条直线上)且相等。
图形的这种移动叫做平移。
图形平移的方向,不限于是水平的。
A
B
C
A/
B/
C/
A
B
C
A/
B/
C/
平移在我们的生活中是很常见的,利用平移也可以制作很多美丽的图案,你能举出生活中一些利用平移的例子吗?
〖例〗 如图,平移△ABC,使点A移动到点A/,
画出平移后的△A/B/C/。
A
B
C
A/
解:连接AA/,过点B作AA/的平行线l,
在l上截取BB/=AA/,
则点B/的就是点B的对应点。
l
B/
类似地,再作出点C的对应点C/,
C/
△A/B/C/就是所要画的图形。
1、如图,△DEF是△ABC经过平移得到的,
则平移的距离是线段 的长度。
A
B
C
D
E
F
BE或CF
课堂练习
2、一个图形经过平移变换后,有以下几种说法,
其中不正确的说法是【 】
(A). 平移后图形的形状和大小都不改变;
(B).平移后的图形与原图形的对应线段平行
(或在同一条直线上)且相等,对应角相等。
(C). 平移后的图形形状不变,但大小可以改变;
(D). 利用基本图形的平移可以设计美丽的图案。
C
3、将长度为10cm的线段向上平移5cm,所得线段
的长度是【 】
A
(A). 10cm (B). 5cm (C). 0 (D). 无法确定。
10cm
10cm
5cm
5cm
4、如图,若△ABC可以看作由△DEF经过平移得到的,已知AB=3,BE=2,则BD等于【 】
(A). 1 (B). 2 (C). 3 (D). 5。
A
B
C
D
E
F
A
5、如图,它是由四个大小、形状完全一样的小三角形组成的,下列不可能实现的情况是【 】
(A). △ADE由△DBF平移得到;
(B).平移△BDF可以得到△FEC;
(C). 平移△EFC可以得到△ADE ;
(D). 通过平移△FEC可以得到△DEF。
D
A
B
C
D
E
F
6、如图, △ABC平移△DEF的位置,有下列结论:⑴ AD=BE=CF,AD∥BE∥CF
⑵ AB∥DE,BC∥EF,AC∥DF
⑶ AB=DE,BC=EF,AC=DF
其中正确的有【 】个
(A). 0; (B). 1; (C). 2; (D). 3。
D
A
B
C
D
E
F
7、如图, 面积为12cm2的△ABC沿BC方向平移到△DEF的位置,平移的距离是边BC长的2倍,则图中四边形ACFD的面积为【 】
(A). 24cm2;
(B). 36cm2;
(C). 48cm2;
(D). 无法确定。
C
A
B
C
D
E
F
G
8、如图,在一块长为am,宽为bm的长方形草地上,有一条弯曲的小路,小路的左边线向右平移1m,就是它的右边线,求这块草地的绿地面积。
a
b
解:(a-1)b
中考链接
1、如图,△DEF是△ABC经过平移得到的,已知∠A=54°,∠ABC=36°,则下列结论不一定成立的是【 】
A
B
C
D
E
F
(A). ∠F=90°
(B). ∠BED=∠FED
(C). BC⊥DF
(D). DF∥AC
B
2、将△ABE的边AE沿所在的直线向右平移4cm,得到梯形ABCD,若△ABE的周长为11cm,则梯形ABCD的周长 。
19cm
A
B
C
D
E
4cm
4cm
3、如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分的面积。
8
24
A
B
C
D
E
F
W
G
H
6
解:由平移可知
S梯形ABCD=S梯形EFGH
∴ S阴影=S梯形DWGH
∵ CW=6cm
∴ DW=24-6=18(cm)
3、如图,把直角梯形ABCD沿AD方向平移到梯形EFGH,HG=24cm,WG=8cm,CW=6cm,求阴影部分的面积。
8
24
A
B
C
D
E
F
W
G
H
6
∵ CW=6cm
∴ DW=24-6=18(cm)
∴ S阴影=(DW+HG)×WG÷2
=(18+24)×8÷2
=168(cm2)
4、如图,⑴ 在3×3网格中,每一个小正方形的边长都是1,△ABC是网格中的等腰三角形,平移△ABC,要求平移后的△ABC各顶点必须在网格的交点上,共可以得到几个这样的三角形(包括△ABC)?
A
B
C
解:在3×3网格中
平移共可得到:4个等腰三角形
4=22
4、如图,⑵在4×4网格中,每一个小正方形的边长都是1,△ABC是网格中的等腰三角形,平移△ABC,要求平移后的△ABC各顶点必须在网格的交点上,共可以得到几个这样的三角形(包括△ABC)?
B
C
解:在4×4网格中
平移共可得到:9个等腰三角形
9=32
A
在5×5网格中
平移共可得到:16个等腰三角形
16=42
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
