5.1.1 相交线(课件)
图片预览




文档简介
(共29张PPT)
5.1.1相交线
人教版 七年级下
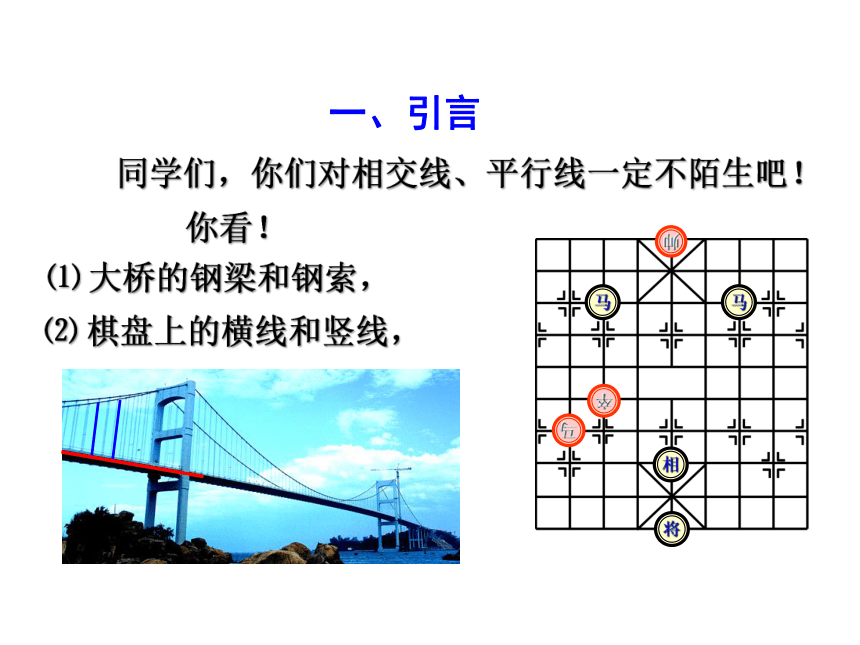
同学们,你们对相交线、平行线一定不陌生吧!
一、引言
你看!
马
马
帅
将
马
卒
相
⑵ 棋盘上的横线和竖线,
⑴ 大桥的钢梁和钢索,
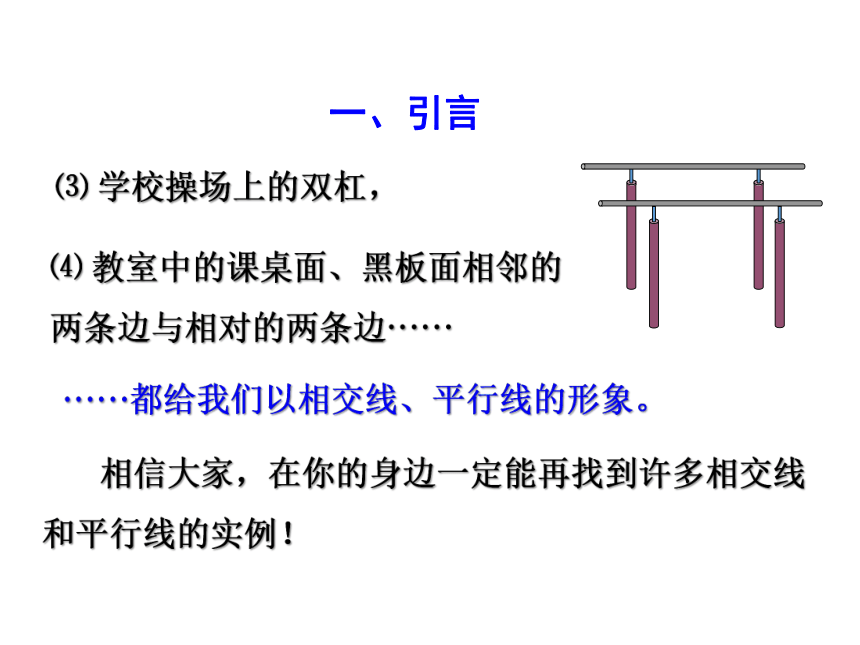
⑶ 学校操场上的双杠,
一、引言
······都给我们以相交线、平行线的形象。
⑷ 教室中的课桌面、黑板面相邻的两条边与相对的两条边······
相信大家,在你的身边一定能再找到许多相交线
和平行线的实例!
在上一章,我们认识了几何图形,并学习了一些基本的平面图形——直线、射线、线段和角。
本章将研究平面内不重合的两条直线的位置关系:
相交与平行
对于相交,我们要研究两条直线相交所成的角的位置关系和数量关系;对于平行,我们要借助于一条直线与另外两条直线相交所成的角,研究平行线的判定和性质。
在此基础上,再学习平移的有关知识,本章我们还将亲历简单推理得出数学结论的方法,培养言之有据的思考习惯。
一、相交线
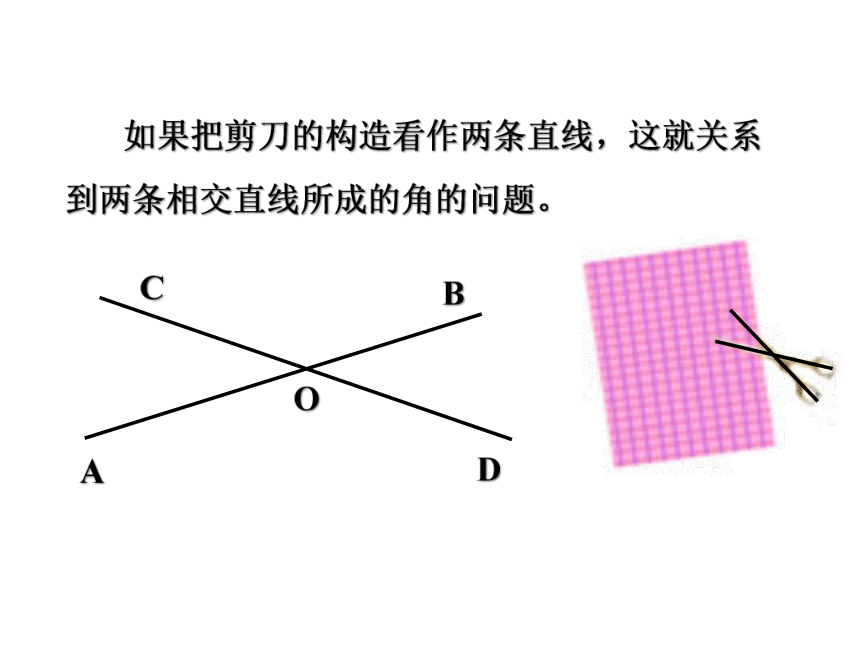
如图,观察剪刀剪开布片的过程中有关角的变化。
可以发现:握紧剪刀的把手时,随着两个把手之间角逐渐变小,剪刀之间的角也相应的变小,直到剪开布片。
如果把剪刀的构造看作两条直线,这就关系到两条相交直线所成的角的问题。
A
B
C
D
O
1
2
3
4
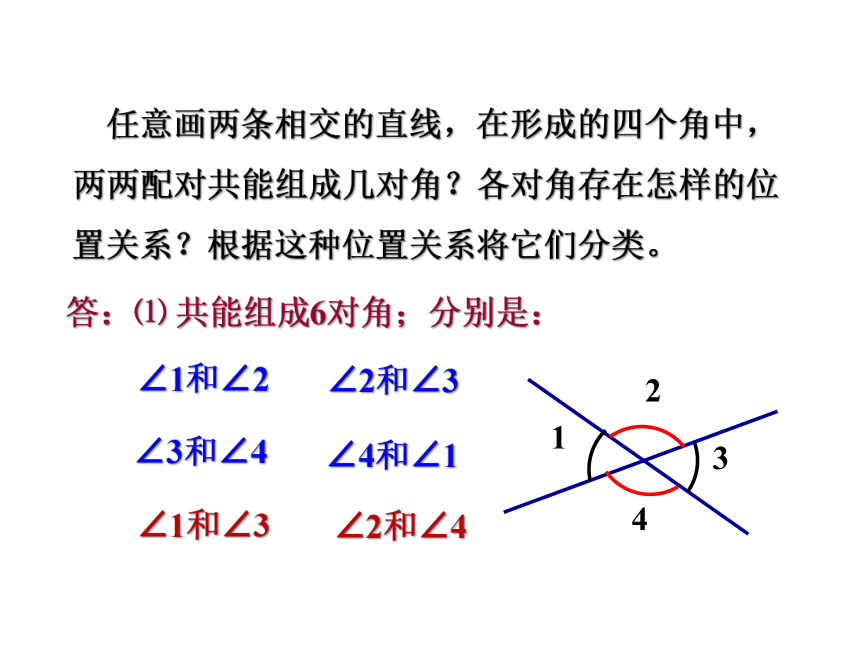
任意画两条相交的直线,在形成的四个角中,两两配对共能组成几对角?各对角存在怎样的位置关系?根据这种位置关系将它们分类。
答:⑴ 共能组成6对角;分别是:
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
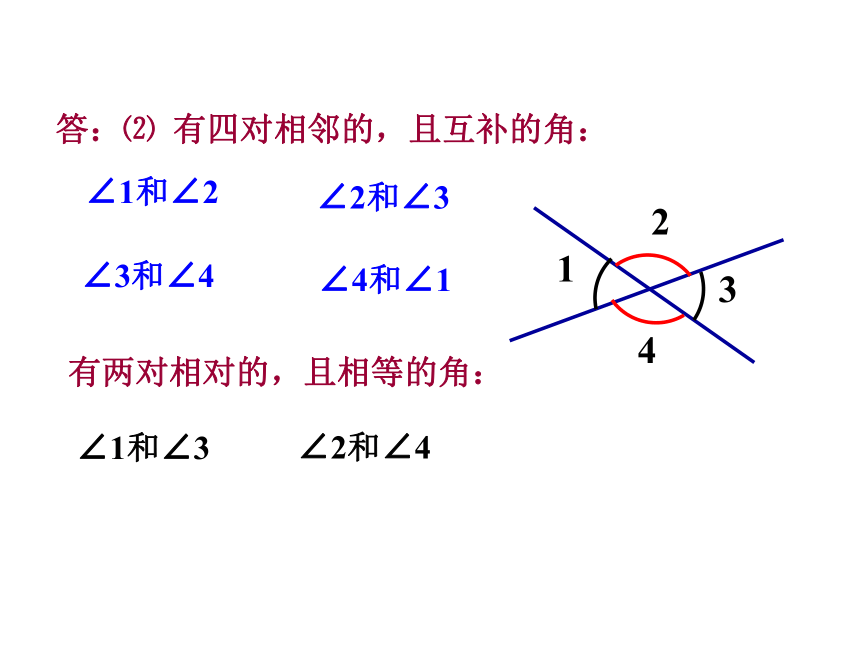
答:⑵ 有四对相邻的,且互补的角:
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
有两对相对的,且相等的角:
1
2
3
4
1
2
答:⑶ ∠1和∠2有一条公共边OC,
A
B
C
O
它们的另一边互为反向延长线.
( ∠1和∠2互补)
具有这种位置关系的两个角,叫做互为邻补角。
以下图形都是互为邻补角:
1
2
A
B
O
C
A
B
C
O
2
1
B
A
C
O
1
2
1
2
3
4
答:⑷ ∠1和∠3 或者 ∠2和∠4
② 并且∠1的两边分别是∠3的两边的
反向延长线,
① 有一个公共的顶点O,
O
具有这种位置关系的两个角,叫做互为对顶角.
A
B
C
D
2、两个角的边互为反向延长线;
【对顶角的本质特征】
1、两个角有公共顶点;
4、对顶角是成对出现的,对顶角是具有特殊
位置关系的两个角。
3、只有当两条直线相交时,才能产生对顶角。
A
B
C
D
O
1
2
【逗你玩】 1、指出下图中的对顶角?
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
2、如图所示,有一个破损的扇形文物,考古学家想知道这个扇形圆心角的度数,你能想一个办法量一量它的度数吗?你的根据是什么?
答:40°
根据是“对顶角相等”
【逗你玩】
答:只要量出∠1的对顶角就可以了!
1
2
∠1=∠2
3、如何测量黑板边沿上边很短的角的度数呢?
【逗你玩】
互为对顶角的两个角有什么关系呢
探究
∵ ∠1+∠2=180°
∠3+∠2=180°
∴∠1=∠3
(同角的补角相等)
对顶角相等
1
2
3
⑴对顶角相等。······〖 〗
⑶有公共顶点且相等的两个角是对顶角。······〖 〗
⑵相等的角是对顶角。 ······〖 〗
⑷不相等的两个角一定不是对顶角。 ······〖 〗
⑸两条直线相交,不相邻的两个角是对顶角。······〖 〗
一、判断题 (在正确的后面打“√”,在错误的后面打“×”)
课堂练习
二、选择题(共1道题)
1、如图,直线AB和CD相交于点O,因为∠1+∠3=180°, ∠2+∠3=180°,所以∠1=∠2,其推理依据是〖 〗
(A) 同角的余角相等;
(B) 同角的补角相等;
(D) 等角的补角相等。
(C) 对顶角相等;
B
A
D
C
O
1
2
3
B
1、若∠β与∠α是对顶角 ,∠α的余角是20°,
则∠β= 。
70°
α
β
解:∵ ∠α的余角是20°
∴ ∠α=90°-20°
=70°
∵ ∠β与∠α是对顶角.
∴ ∠β=∠α=70°
三、填空题(共3道题)
2、如图,直线AB与CD相交于点O, OA平分∠EOC, ∠EOC=70°,则∠BOD= , ∠BOC= 。
35°
145°
A
B
O
E
D
C
解: ∵OA平分∠EOC
=35°
∴∠AOC= ∠EOC
∴∠BOD=∠AOC
=35°
∠BOC=180°-∠AOC
=145°
3、如图,OA⊥OB,OC⊥OD,∠COB=50°,
则∠AOD= 。
130°
A
O
B
C
D
解: ∠AOC=90°- ∠COB
=90°- 50°
=40°
∠AOD=90°+40°
=130°
40°
1、如图,在长方形的台球桌面上,∠1+∠3=90°
∠ 2=∠3。已知∠2=58°,求∠1的度数。
答: ∠1= 32°
理由:∠1=90°-∠3
= 90°-∠2
= 90°-58 °
=32 °
解答题(共3道题)
2、当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象(如图所示)。图中∠1与∠2是对顶角吗?为什么?
答:∠1和∠2 不是对顶角。
因为:∠2的一条边不是∠1的反向延长线。
1
2
3、在长方形的台球桌面上,选择恰当的角度击打白球,可以使白球经过两次反弹后将红球直接撞入袋中。此时∠1=∠2,∠3 =∠4 ,并且∠2+∠3=90 °,∠4+∠5=90°。如果红球与洞口的连线和台球桌面边缘的夹角∠5=40 °,那么∠1应等于多少度才能保证红球准确入袋?请说明理由。
1
5
2
3
4
3、在长方形的台球桌面上,选择恰当的角度击打白球,可以使白球经过两次反弹后将红球直接撞入袋中。此时∠1=∠2,∠3 =∠4 ,并且∠2+∠3=90 °,∠4+∠5=90°。如果红球与洞口的连线和台球桌面边缘的夹角∠5=40 °,那么∠1应等于多少度才能保证红球准确入袋?请说明理由。
解:∵∠1=∠2,∠3=∠4
∠2+∠3=90 °
∴∠1+∠4=90 °
∵∠4+∠5=90 °
∴∠1=∠5=40 °
1
5
2
3
4
答:∠1=40 °才能保证红球准确入袋。
有四对邻补角,两对对顶角。
3、不重合的两条直线相交形成四个角
归纳与整理
对顶角的定义 → 对顶角相等.
2、互为补角→互为邻补角的定义
1、①同角或等角的余角相等;
②同角或等角的补角相等。
谢谢
5.1.1相交线
人教版 七年级下
同学们,你们对相交线、平行线一定不陌生吧!
一、引言
你看!
马
马
帅
将
马
卒
相
⑵ 棋盘上的横线和竖线,
⑴ 大桥的钢梁和钢索,
⑶ 学校操场上的双杠,
一、引言
······都给我们以相交线、平行线的形象。
⑷ 教室中的课桌面、黑板面相邻的两条边与相对的两条边······
相信大家,在你的身边一定能再找到许多相交线
和平行线的实例!
在上一章,我们认识了几何图形,并学习了一些基本的平面图形——直线、射线、线段和角。
本章将研究平面内不重合的两条直线的位置关系:
相交与平行
对于相交,我们要研究两条直线相交所成的角的位置关系和数量关系;对于平行,我们要借助于一条直线与另外两条直线相交所成的角,研究平行线的判定和性质。
在此基础上,再学习平移的有关知识,本章我们还将亲历简单推理得出数学结论的方法,培养言之有据的思考习惯。
一、相交线
如图,观察剪刀剪开布片的过程中有关角的变化。
可以发现:握紧剪刀的把手时,随着两个把手之间角逐渐变小,剪刀之间的角也相应的变小,直到剪开布片。
如果把剪刀的构造看作两条直线,这就关系到两条相交直线所成的角的问题。
A
B
C
D
O
1
2
3
4
任意画两条相交的直线,在形成的四个角中,两两配对共能组成几对角?各对角存在怎样的位置关系?根据这种位置关系将它们分类。
答:⑴ 共能组成6对角;分别是:
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
答:⑵ 有四对相邻的,且互补的角:
∠1和∠2
∠2和∠3
∠3和∠4
∠4和∠1
∠1和∠3
∠2和∠4
有两对相对的,且相等的角:
1
2
3
4
1
2
答:⑶ ∠1和∠2有一条公共边OC,
A
B
C
O
它们的另一边互为反向延长线.
( ∠1和∠2互补)
具有这种位置关系的两个角,叫做互为邻补角。
以下图形都是互为邻补角:
1
2
A
B
O
C
A
B
C
O
2
1
B
A
C
O
1
2
1
2
3
4
答:⑷ ∠1和∠3 或者 ∠2和∠4
② 并且∠1的两边分别是∠3的两边的
反向延长线,
① 有一个公共的顶点O,
O
具有这种位置关系的两个角,叫做互为对顶角.
A
B
C
D
2、两个角的边互为反向延长线;
【对顶角的本质特征】
1、两个角有公共顶点;
4、对顶角是成对出现的,对顶角是具有特殊
位置关系的两个角。
3、只有当两条直线相交时,才能产生对顶角。
A
B
C
D
O
1
2
【逗你玩】 1、指出下图中的对顶角?
O
A
B
C
D
O
A
B
C
D
O
A
B
C
D
2、如图所示,有一个破损的扇形文物,考古学家想知道这个扇形圆心角的度数,你能想一个办法量一量它的度数吗?你的根据是什么?
答:40°
根据是“对顶角相等”
【逗你玩】
答:只要量出∠1的对顶角就可以了!
1
2
∠1=∠2
3、如何测量黑板边沿上边很短的角的度数呢?
【逗你玩】
互为对顶角的两个角有什么关系呢
探究
∵ ∠1+∠2=180°
∠3+∠2=180°
∴∠1=∠3
(同角的补角相等)
对顶角相等
1
2
3
⑴对顶角相等。······〖 〗
⑶有公共顶点且相等的两个角是对顶角。······〖 〗
⑵相等的角是对顶角。 ······〖 〗
⑷不相等的两个角一定不是对顶角。 ······〖 〗
⑸两条直线相交,不相邻的两个角是对顶角。······〖 〗
一、判断题 (在正确的后面打“√”,在错误的后面打“×”)
课堂练习
二、选择题(共1道题)
1、如图,直线AB和CD相交于点O,因为∠1+∠3=180°, ∠2+∠3=180°,所以∠1=∠2,其推理依据是〖 〗
(A) 同角的余角相等;
(B) 同角的补角相等;
(D) 等角的补角相等。
(C) 对顶角相等;
B
A
D
C
O
1
2
3
B
1、若∠β与∠α是对顶角 ,∠α的余角是20°,
则∠β= 。
70°
α
β
解:∵ ∠α的余角是20°
∴ ∠α=90°-20°
=70°
∵ ∠β与∠α是对顶角.
∴ ∠β=∠α=70°
三、填空题(共3道题)
2、如图,直线AB与CD相交于点O, OA平分∠EOC, ∠EOC=70°,则∠BOD= , ∠BOC= 。
35°
145°
A
B
O
E
D
C
解: ∵OA平分∠EOC
=35°
∴∠AOC= ∠EOC
∴∠BOD=∠AOC
=35°
∠BOC=180°-∠AOC
=145°
3、如图,OA⊥OB,OC⊥OD,∠COB=50°,
则∠AOD= 。
130°
A
O
B
C
D
解: ∠AOC=90°- ∠COB
=90°- 50°
=40°
∠AOD=90°+40°
=130°
40°
1、如图,在长方形的台球桌面上,∠1+∠3=90°
∠ 2=∠3。已知∠2=58°,求∠1的度数。
答: ∠1= 32°
理由:∠1=90°-∠3
= 90°-∠2
= 90°-58 °
=32 °
解答题(共3道题)
2、当光线从空气射入水中时,光线的传播方向发生了改变,这就是折射现象(如图所示)。图中∠1与∠2是对顶角吗?为什么?
答:∠1和∠2 不是对顶角。
因为:∠2的一条边不是∠1的反向延长线。
1
2
3、在长方形的台球桌面上,选择恰当的角度击打白球,可以使白球经过两次反弹后将红球直接撞入袋中。此时∠1=∠2,∠3 =∠4 ,并且∠2+∠3=90 °,∠4+∠5=90°。如果红球与洞口的连线和台球桌面边缘的夹角∠5=40 °,那么∠1应等于多少度才能保证红球准确入袋?请说明理由。
1
5
2
3
4
3、在长方形的台球桌面上,选择恰当的角度击打白球,可以使白球经过两次反弹后将红球直接撞入袋中。此时∠1=∠2,∠3 =∠4 ,并且∠2+∠3=90 °,∠4+∠5=90°。如果红球与洞口的连线和台球桌面边缘的夹角∠5=40 °,那么∠1应等于多少度才能保证红球准确入袋?请说明理由。
解:∵∠1=∠2,∠3=∠4
∠2+∠3=90 °
∴∠1+∠4=90 °
∵∠4+∠5=90 °
∴∠1=∠5=40 °
1
5
2
3
4
答:∠1=40 °才能保证红球准确入袋。
有四对邻补角,两对对顶角。
3、不重合的两条直线相交形成四个角
归纳与整理
对顶角的定义 → 对顶角相等.
2、互为补角→互为邻补角的定义
1、①同角或等角的余角相等;
②同角或等角的补角相等。
谢谢
