人教版高中数学必修一1.1.3《集合的基本运算》教学课件 (共22张PPT)
文档属性
| 名称 | 人教版高中数学必修一1.1.3《集合的基本运算》教学课件 (共22张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 477.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-02 00:00:00 | ||
图片预览






文档简介
课件22张PPT。1.1.3集合的基本运算观察集合A,B,C元素间的关系: A={4,5,6,8},
B={3,5,7,8},
C={3,4,5,6,7,8}
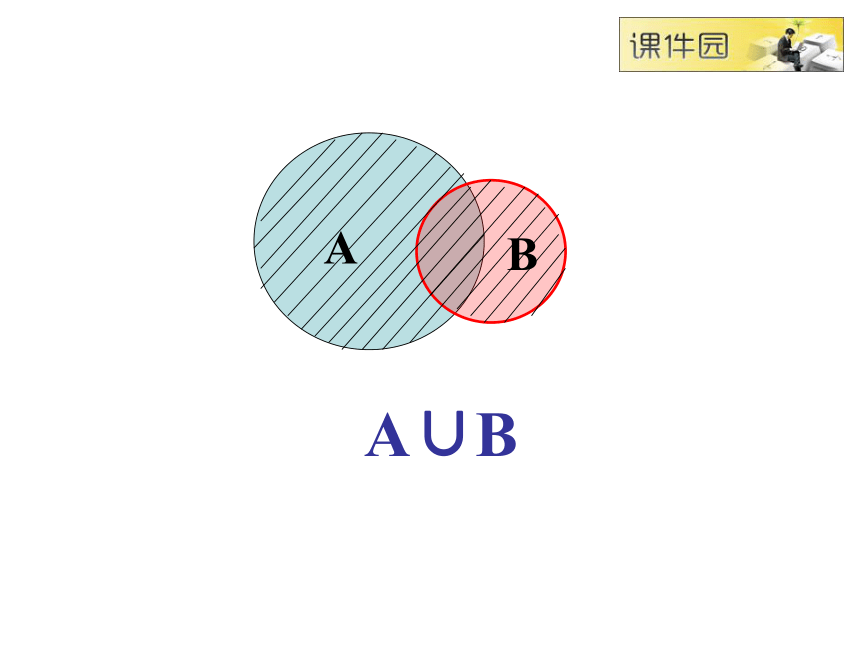
定 义一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,
记作 A∪B即A∪B={x x∈A,或x∈B} 读作 A并 BABA∪B例4设集合A={4,5,6,8},
集合B={3,5,7,8,9},
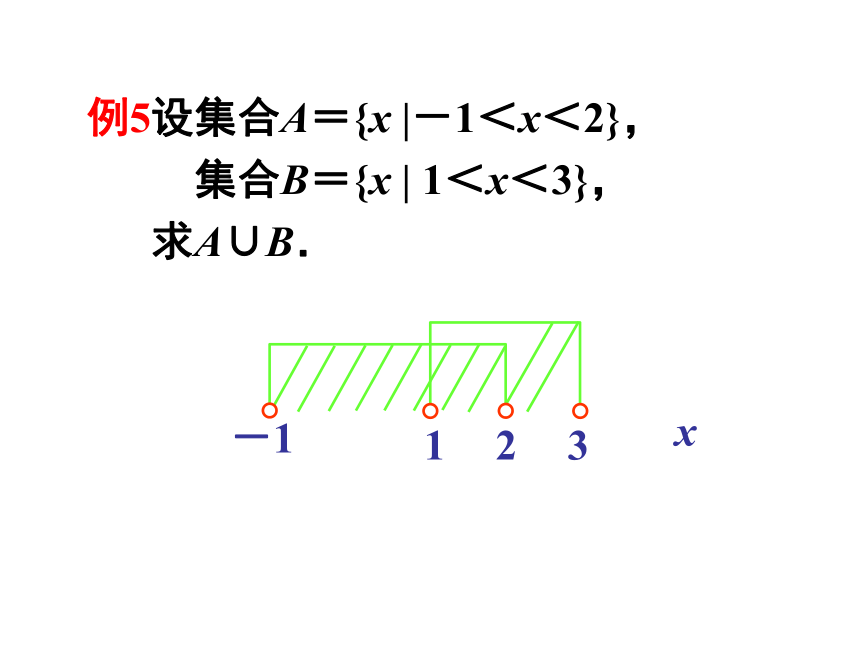
求A∪B.A∪B={3,4,5,6,7,8,9}.例5设集合A={x |-1<x<2},
集合B={x | 1<x<3},
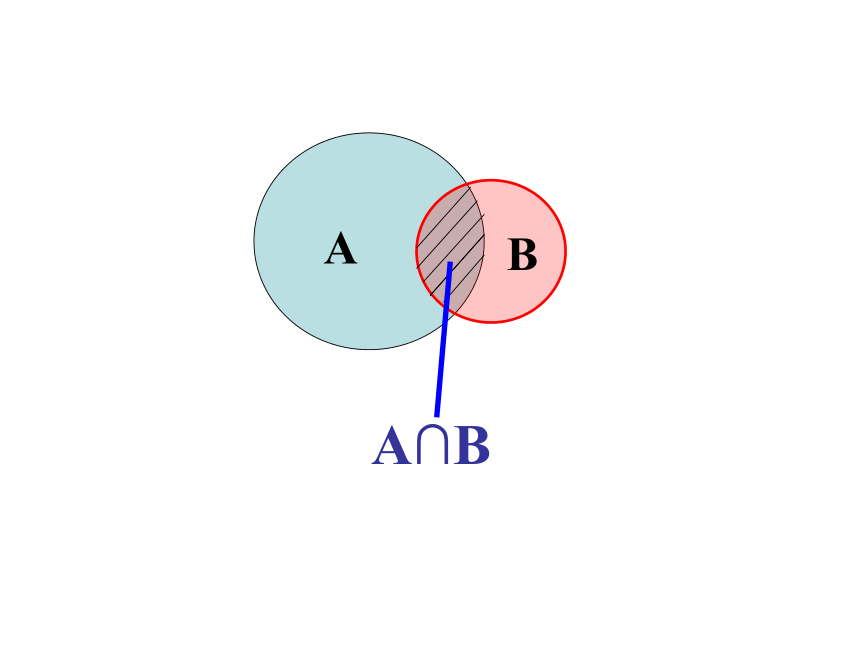
求A∪B.x-1123定 义一般地,由既属于集合A又属于集合B的所有元素组成的集合叫做A与B的交集.记作 A∩B 即 A∩B={x x∈A,且x∈B} 读作 A交 BABA∩B性 质⑴ A∩A = A∩φ = ⑵ A∪A = A∪φ =AAφA==A∪B B∪AA∩B B∩A例6 新华中学开运动会。设
A={x |x是新华中学高一年级参加百米赛的同学},
B={x |x是新华中学高一年级参加跳高比赛的同学},
求A∩B.解: A∩B={x |x是新华中学高一年级中既参加百米赛
的同学又参加跳高比赛的同学}。
例题讲解例7.设L1,L2分别是平面内两条直线l1和l2上点的集合,试用集合的运算表示这两条直线的位置关系。解:
当两条直线l1、l2相交于一点P时,L1∩L2={点P};
当两条直线l1、l2平行时,L1∩L2=Φ;
当两条直线l1、l2重合时,L1∩L2= L1=L2。练习: 设A={x x是等腰三角形},B={x x是直角三角形},则A∩B={等腰直角三角形}如:S={1,2,3,4,5,6}
A={1,3,5}
一般地,如果一个集合 中含有我们所要研究问题中的全部元素, 我们把它叫做
全集.{2,4,6}.全 集 一般地,设S是一个集合,A是S中
的一个子集, 即A?S ,则由S中所有不
属于A的元素组成的集合,叫做S中集合
A的补集(或余集),记作:补 集 对于一个集合A,由全集U中不
属于A的元素所有元素组成的集合,成为集合A相对于全集U的补集,简称为集合A的补集,记作:补 集例8:设U={x1,2,3,4,5,6}
A={1,3,5}
?如:S={1,2,3,4,5,6}
A={1,3,5}
{2,4,6}. 研究补集必须是在全集的条件下研
究,而全集因研究问题不同而异,全集
常用U来表示.注意:补集可以看成是集合的一种“运算”,它具有以下性质:若全集为U,A?U,则?UA练习7练习课堂小结1. 理解两个集合交集与并集补集的概念bb和性质. 2. 求两个集合的运算,常用 bbb数轴法和图示法.4. 注意对字母要进行讨论 . 3.注意灵活、准确地运用性质解题;教材P12 A组T6,7祝你愉快作业布置B组T3,课件22张PPT。1.1.3集合的基本运算观察集合A,B,C元素间的关系: A={4,5,6,8},
B={3,5,7,8},
C={3,4,5,6,7,8}
定 义一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,
记作 A∪B即A∪B={x x∈A,或x∈B} 读作 A并 BABA∪B例4设集合A={4,5,6,8},
集合B={3,5,7,8,9},
求A∪B.A∪B={3,4,5,6,7,8,9}.例5设集合A={x |-1<x<2},
集合B={x | 1<x<3},
求A∪B.x-1123定 义一般地,由既属于集合A又属于集合B的所有元素组成的集合叫做A与B的交集.记作 A∩B 即 A∩B={x x∈A,且x∈B} 读作 A交 BABA∩B性 质⑴ A∩A = A∩φ = ⑵ A∪A = A∪φ =AAφA==A∪B B∪AA∩B B∩A例6 新华中学开运动会。设
A={x |x是新华中学高一年级参加百米赛的同学},
B={x |x是新华中学高一年级参加跳高比赛的同学},
求A∩B.解: A∩B={x |x是新华中学高一年级中既参加百米赛
的同学又参加跳高比赛的同学}。
例题讲解例7.设L1,L2分别是平面内两条直线l1和l2上点的集合,试用集合的运算表示这两条直线的位置关系。解:
当两条直线l1、l2相交于一点P时,L1∩L2={点P};
当两条直线l1、l2平行时,L1∩L2=Φ;
当两条直线l1、l2重合时,L1∩L2= L1=L2。练习: 设A={x x是等腰三角形},B={x x是直角三角形},则A∩B={等腰直角三角形}如:S={1,2,3,4,5,6}
A={1,3,5}
一般地,如果一个集合 中含有我们所要研究问题中的全部元素, 我们把它叫做
全集.{2,4,6}.全 集 一般地,设S是一个集合,A是S中
的一个子集, 即A?S ,则由S中所有不
属于A的元素组成的集合,叫做S中集合
A的补集(或余集),记作:补 集 对于一个集合A,由全集U中不
属于A的元素所有元素组成的集合,成为集合A相对于全集U的补集,简称为集合A的补集,记作:补 集例8:设U={x1,2,3,4,5,6}
A={1,3,5}
?如:S={1,2,3,4,5,6}
A={1,3,5}
{2,4,6}. 研究补集必须是在全集的条件下研
究,而全集因研究问题不同而异,全集
常用U来表示.注意:补集可以看成是集合的一种“运算”,它具有以下性质:若全集为U,A?U,则?UA练习7练习课堂小结1. 理解两个集合交集与并集补集的概念bb和性质. 2. 求两个集合的运算,常用 bbb数轴法和图示法.4. 注意对字母要进行讨论 . 3.注意灵活、准确地运用性质解题;教材P12 A组T6,7祝你愉快作业布置B组T3,
B={3,5,7,8},
C={3,4,5,6,7,8}
定 义一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,
记作 A∪B即A∪B={x x∈A,或x∈B} 读作 A并 BABA∪B例4设集合A={4,5,6,8},
集合B={3,5,7,8,9},
求A∪B.A∪B={3,4,5,6,7,8,9}.例5设集合A={x |-1<x<2},
集合B={x | 1<x<3},
求A∪B.x-1123定 义一般地,由既属于集合A又属于集合B的所有元素组成的集合叫做A与B的交集.记作 A∩B 即 A∩B={x x∈A,且x∈B} 读作 A交 BABA∩B性 质⑴ A∩A = A∩φ = ⑵ A∪A = A∪φ =AAφA==A∪B B∪AA∩B B∩A例6 新华中学开运动会。设
A={x |x是新华中学高一年级参加百米赛的同学},
B={x |x是新华中学高一年级参加跳高比赛的同学},
求A∩B.解: A∩B={x |x是新华中学高一年级中既参加百米赛
的同学又参加跳高比赛的同学}。
例题讲解例7.设L1,L2分别是平面内两条直线l1和l2上点的集合,试用集合的运算表示这两条直线的位置关系。解:
当两条直线l1、l2相交于一点P时,L1∩L2={点P};
当两条直线l1、l2平行时,L1∩L2=Φ;
当两条直线l1、l2重合时,L1∩L2= L1=L2。练习: 设A={x x是等腰三角形},B={x x是直角三角形},则A∩B={等腰直角三角形}如:S={1,2,3,4,5,6}
A={1,3,5}
一般地,如果一个集合 中含有我们所要研究问题中的全部元素, 我们把它叫做
全集.{2,4,6}.全 集 一般地,设S是一个集合,A是S中
的一个子集, 即A?S ,则由S中所有不
属于A的元素组成的集合,叫做S中集合
A的补集(或余集),记作:补 集 对于一个集合A,由全集U中不
属于A的元素所有元素组成的集合,成为集合A相对于全集U的补集,简称为集合A的补集,记作:补 集例8:设U={x1,2,3,4,5,6}
A={1,3,5}
?如:S={1,2,3,4,5,6}
A={1,3,5}
{2,4,6}. 研究补集必须是在全集的条件下研
究,而全集因研究问题不同而异,全集
常用U来表示.注意:补集可以看成是集合的一种“运算”,它具有以下性质:若全集为U,A?U,则?UA练习7练习课堂小结1. 理解两个集合交集与并集补集的概念bb和性质. 2. 求两个集合的运算,常用 bbb数轴法和图示法.4. 注意对字母要进行讨论 . 3.注意灵活、准确地运用性质解题;教材P12 A组T6,7祝你愉快作业布置B组T3,课件22张PPT。1.1.3集合的基本运算观察集合A,B,C元素间的关系: A={4,5,6,8},
B={3,5,7,8},
C={3,4,5,6,7,8}
定 义一般地,由属于集合A或属于集合B的所有元素组成的集合叫做A与B的并集,
记作 A∪B即A∪B={x x∈A,或x∈B} 读作 A并 BABA∪B例4设集合A={4,5,6,8},
集合B={3,5,7,8,9},
求A∪B.A∪B={3,4,5,6,7,8,9}.例5设集合A={x |-1<x<2},
集合B={x | 1<x<3},
求A∪B.x-1123定 义一般地,由既属于集合A又属于集合B的所有元素组成的集合叫做A与B的交集.记作 A∩B 即 A∩B={x x∈A,且x∈B} 读作 A交 BABA∩B性 质⑴ A∩A = A∩φ = ⑵ A∪A = A∪φ =AAφA==A∪B B∪AA∩B B∩A例6 新华中学开运动会。设
A={x |x是新华中学高一年级参加百米赛的同学},
B={x |x是新华中学高一年级参加跳高比赛的同学},
求A∩B.解: A∩B={x |x是新华中学高一年级中既参加百米赛
的同学又参加跳高比赛的同学}。
例题讲解例7.设L1,L2分别是平面内两条直线l1和l2上点的集合,试用集合的运算表示这两条直线的位置关系。解:
当两条直线l1、l2相交于一点P时,L1∩L2={点P};
当两条直线l1、l2平行时,L1∩L2=Φ;
当两条直线l1、l2重合时,L1∩L2= L1=L2。练习: 设A={x x是等腰三角形},B={x x是直角三角形},则A∩B={等腰直角三角形}如:S={1,2,3,4,5,6}
A={1,3,5}
一般地,如果一个集合 中含有我们所要研究问题中的全部元素, 我们把它叫做
全集.{2,4,6}.全 集 一般地,设S是一个集合,A是S中
的一个子集, 即A?S ,则由S中所有不
属于A的元素组成的集合,叫做S中集合
A的补集(或余集),记作:补 集 对于一个集合A,由全集U中不
属于A的元素所有元素组成的集合,成为集合A相对于全集U的补集,简称为集合A的补集,记作:补 集例8:设U={x1,2,3,4,5,6}
A={1,3,5}
?如:S={1,2,3,4,5,6}
A={1,3,5}
{2,4,6}. 研究补集必须是在全集的条件下研
究,而全集因研究问题不同而异,全集
常用U来表示.注意:补集可以看成是集合的一种“运算”,它具有以下性质:若全集为U,A?U,则?UA练习7练习课堂小结1. 理解两个集合交集与并集补集的概念bb和性质. 2. 求两个集合的运算,常用 bbb数轴法和图示法.4. 注意对字母要进行讨论 . 3.注意灵活、准确地运用性质解题;教材P12 A组T6,7祝你愉快作业布置B组T3,
