16.3 二次根式的加减(2)同步练习
文档属性
| 名称 | 16.3 二次根式的加减(2)同步练习 |  | |
| 格式 | docx | ||
| 文件大小 | 524.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-02 17:05:57 | ||
图片预览



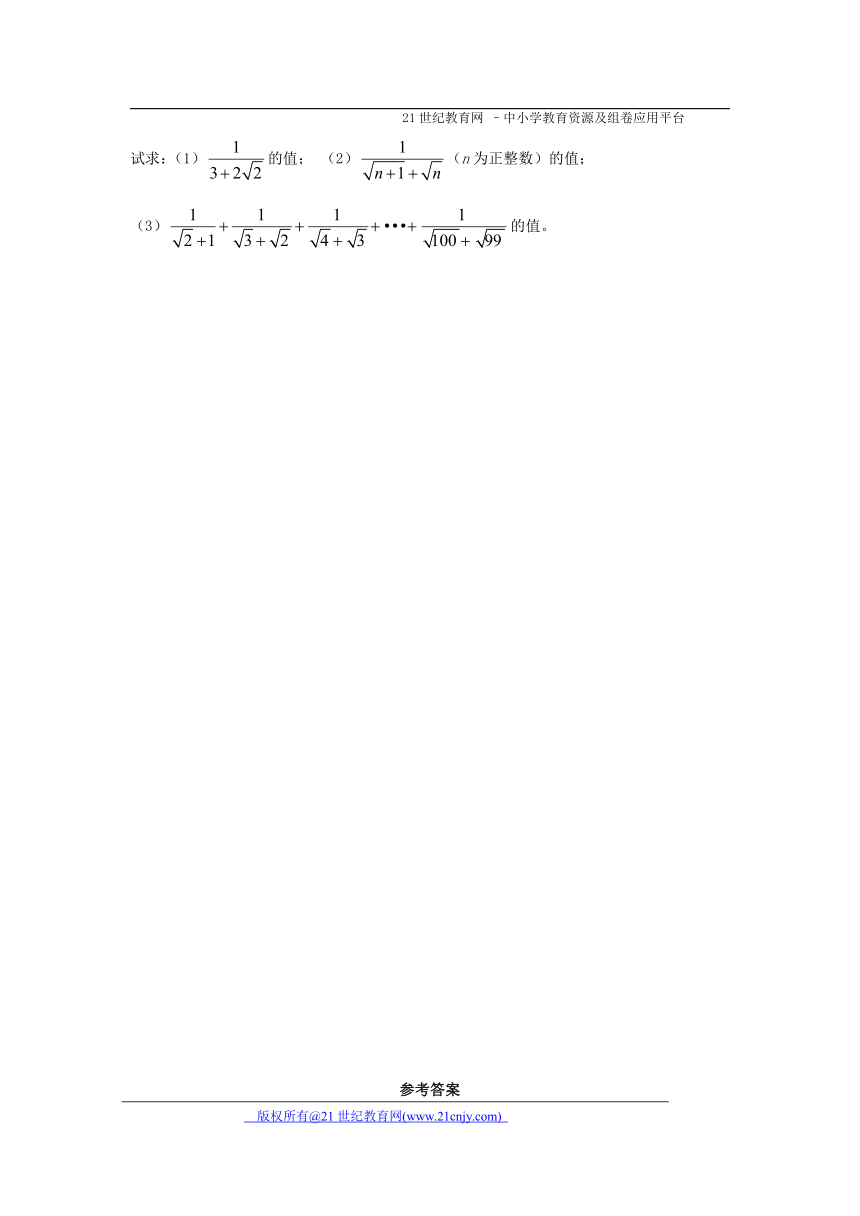

文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
16.3二次根式的加减(2)同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
1.二次根式的混合运算
(1)在二次根式的运算中,实数的运算性质和法则同样适用.
(2)二次根式的混合运算顺序与实数中的运算顺序一样,先算乘方、开方,再算乘除,最后算加减 ,有括号的先算括号里的.
2. 进行二次根式的混合运算时,一般先将二次根式转化为最简二次根式,再根据题目的特点确定合理的运算方法,同时要灵活运用乘法公式、因式分解等简化计算.
基础知识和能力拓展训练
一、选择题
1.下列计算正确的是( )
A. B. C.3+=4 D.×(﹣)=3
2.估计的运算结果应在( )之间.
A. 1和2 B. 2和3 C. 3和4 D. 4和5
3.若且,则化简的结果为( )
A. 4a B. 6x-2a C. 2x+2a D. 2a-2x
4.若三角形的面积为12,一条边的长为+1,则这条边上的高为( )
A. 12+12 B. 24-24 C. 12-12 D. 24+24
5.已知,则x等于( )
A. 4 B. ±2 C. 2 D. ±4
6.若a、b、c为有理数,且等式成立,则2a+999b+1001c的值是( )
A. 1999 B. 2000 C. 2001 D. 不能确定
7.化简 结果正确的是( )
A. 3+2 B. 3- C. 17+12 D. 17-12
8.若3,m,5为三角形三边,化简: 得( ).
A. -10 B. -2m+6 C. -2m-6 D. 2m-10
9.观察下列等式:①=1+-=;②=1+-=;③.根据上面三个等式提供的信息,请猜想的结果为( )
A. B. C. D.
二、填空题
10.计算: =________
11.已知﹣=2,则的值为_____.
12.的整数部分是x,小数部分是y,则y(x+)的值为________ .
13.当x=2+时,式子x2﹣4x+2017=________.
14.对于任意实数a,b,定义一种运算“◇”如下:a◇b=a(a-b)+b(a+b),如:3◇2=3×(3-2)+2×(3+2)=13,那么◇=_____.
15.已知a、b、c是△ABC的三边,则的值为________.
16.不等式(1-)x>1+的最大整数解是________.
17.设a,b是有理数,且满足等式,则__________.
18.将一组数,2,,2,,…,2按图中的方法排列:
若3的位置记为(2,3),2的位置记为(3,2),则这组数中最大数的位置记为______.
三、解答题
19.计算:
(1)9÷×;
(2)( --)×(-2);
(3) ++-+;
(4)(3-)2(3+)+(3+)2(3-).
20.化简 .
21.一圆形转盘的面积是25.12cm2,该圆形转盘的半径是多少?(π取3.14)
22.已知: , ,求代数式的值.
23.若a,b为实数,且++>b,化简|2b-1|-.
24.先化简,再求值,其中a=,b=.
25.阅读下面问题:
;
;……
试求:(1)的值; (2)(n为正整数)的值;
(3)的值。
参考答案
1.C
【解析】A选项中, ,故A错误;
B选项中, ,故B错误;
C选项中, ,故C正确;
D选项中, ,故D错误;
∴选C.
2.C
【解析】=
,1.4<
所以3.1<。
故选C.
3.A
【解析】解:∵﹣2a<x<﹣a,a>x,∴x+a<0,x+2a>0,x﹣a<0,∴原式=﹣(x+a)+ +2(x+2a)=﹣x﹣a+2x+4a+|x﹣a|=x+3a+|x﹣a|=x+3a﹣x+a=4a.故选A.
点睛:解答此题,要弄清两个问题:(1)定义:一般地,形如(a≥0)的代数式叫做二次根式.当a>0时, 表示a的算术平方根,当a=0时, =0,当a小于0时,二次根式无意义;(2)性质: =|a|.
4.B
【解析】设高为h,根据题意得: (+1)h=12,
h===24-24,
故选:B.
5.C
【解析】试题解析:已知,
∴x>0,
∴原式可化简为: ,
∴,
两边平方得:2x=4,
∴x=2,
故选C.
6.B
【解析】因 =,所以a=0,b=1,c=1,即可得2a+999b+1001c=999+1001=2000,故选B.
点睛:本题考查了二次根式的性质与化简,将复合二次根式根据完全平方公式化简并比较系数是解题的关键.
7.A
【解析】试题解析: =.
故选A.
8.D
【解析】根据题意,得:2∴2 m<0,m 8<0,
∴原式=m 2+m 8=2m 10.故选D.
9.D
【解析】====,
故选:D.
点睛:本题属于探索规律型,主要考查学生的观察及学习能力,并根据观察总结规律的能力.
10.6
【解析】试题解析: 原式=(+2)×
=3×
=6.
故答案为6.
11.4
【解析】∵﹣=2,
∴(﹣)2=4,
∴x+=6,
∴(x+)2=36,
∴+=34,
∴=.
故答案为:4.
点睛:对于化简求值题,关键是要认真分析题目中的隐含条件,挖掘已知条件与结论之间的内在关系与联系,进行适当化简,再求值中要注意有关性质、公式、运算法则的灵活运用,在求值后还要注意检查.
12.1
【解析】分析:本题考查的是无理数的整数部分和小数部分的相关计算,小数部分要用原数减去整数部分.
解析:∵ 的整数部分是3,∴小数部分是: -3,∴x=3,y=-3,∴y(x+)= .
故答案为1.
13.2016
【解析】把所求的式子化成(x﹣2)2+2013然后代入式子计算,即可得到:x2﹣4x+2017=(x﹣2)2+2013 =()2+2013=3+2013=2016.
故答案是:2016.
点睛:此题主要考查了配方法的应用,解题关键是把式子配成完全平方,然后整体代入即可求解,考查了学生对整体思想的认识和应用,学生对整体思想不熟时出错的主要原因.
14.5
【解析】◇==5.
故本题应填5.
点睛:理解新定义运算的运算规则,其实就是一个对应关系,a对应,b对应,即将a=,b=,代入到代数式a(a-b)+b(a+b)中,再根据二次根式的混合运算法则进行计算,注意最终的结果一定要化为最简二次根式.
15.2c-2a
【解析】∵a,b,c分别是△ABC的三边,
∴ac,
∴=b+c a a b+c=2c 2a,
故答案为:2c-2a.
16.-4
【解析】不等式(1-)x>1+两边同乘以1+得:(1-3)x>4+2,
解得x<-2-,
∵-4<-2-3√<-3,
∴最大整数解是-4.
故答案为:-4.
17.1或
【解析】b=-5, ,
a=,
或者-11.
18.(17,6)
【解析】观察、分析这组数据可发现:第一个数是的积;第二个数是的积;第三个数是的积, 的积.
∵这组数据中最大的数:,
∴是这组数据中的第102个数.
∵每一行排列了6个数,而
∴是第17行第6个数,
∴这组数据中最大的一个数应记为(17,6).
点睛:(1)这组数据组中的第个数为;(2)该组数据是按从左到右,从小到大,每行6个数进行排列的;(3)的商是数据所在的行数,的余数是数据所在的列数.
19.(1) (2)2(3)-(4)42
【解析】试题分析:(1)利用二次根式的乘除运算法则计算.(2)先化成最简二次根式,再计算.(3) 先化成最简二次根式,再计算.(4)利用公式提取公因式,再求值.
试题解析:
(1)9÷×=9=3.
(2)( --)×(-2)==2.
(3) ++-+=+=.
(4)(3-)2(3+)+(3+)2(3-)=(3-)(3+)(3-)=(9-2)6=42.
20.
【解析】试题分析:括号内先进行约分运算,然后通分进行加减运算后进行乘法运算,最后与前面的式子通分进行加减运算即可得.
试题解析:原式=
=
=
= .
21.该圆形转盘的半径是2 cm.
【解析】试题分析:设该圆形转盘的半径是Rcm,根据圆的面积公式得出R.
解:设该圆形转盘的半径是Rcm,
根据题意得πR2=25.12,
∴R2=8,
∴R=2,
答:该圆形转盘的半径是2 cm.
22.
【解析】试题分析:由题意列二元一次方程组,分别求出x、y的值,再将x、y的值代入要求的式子即可.
试题解析:
由题意得: ,
解得,
∴==.
点睛:本题关键在于根据根式的性质列出方程组.
23.-b
【解析】试题解析:先由+成立,得a=1,所以b<,再根据负数的绝对值是它的相反数和=|a|进行化简.
试题解析:由题意得,
解得a=1,故b<,
∴2b-1<0,b-1<0,
∴|2b-1|-=1-2b-|b-1|=1-2b-(1-b)=-b.
24.,
【解析】试题分析:先根据分式混合运算的法则把原式进行化简,再把a、b的值代入进行计算即可.
试题解析:原式=
=
= ,
当a=,b=时,a+b==,
所以原式=.
点睛:本题考查了分式的化简求值:先把各分式的分子或分母因式分解,再进行分式的乘除运算,然后进行分式的加减运算得到最简分式或整式,再把满足条件的字母的值代入计算得到对应的分式的值;有括号先算括号.也考查了二次根式的计算.
25.(1)3-2;
(2)
(3)9
【解析】试题分析:根据题意给出的过程即可求出答案.
试题解析:解:(1)
(2)
(3)原式===10-1=9
点睛:本题考查分母有理化,解题的关键是熟练运用二次根式的性质,本题属于基础题型.
版权所有@21世纪教育网(www.21cnjy.com)
16.3二次根式的加减(2)同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
1.二次根式的混合运算
(1)在二次根式的运算中,实数的运算性质和法则同样适用.
(2)二次根式的混合运算顺序与实数中的运算顺序一样,先算乘方、开方,再算乘除,最后算加减 ,有括号的先算括号里的.
2. 进行二次根式的混合运算时,一般先将二次根式转化为最简二次根式,再根据题目的特点确定合理的运算方法,同时要灵活运用乘法公式、因式分解等简化计算.
基础知识和能力拓展训练
一、选择题
1.下列计算正确的是( )
A. B. C.3+=4 D.×(﹣)=3
2.估计的运算结果应在( )之间.
A. 1和2 B. 2和3 C. 3和4 D. 4和5
3.若且,则化简的结果为( )
A. 4a B. 6x-2a C. 2x+2a D. 2a-2x
4.若三角形的面积为12,一条边的长为+1,则这条边上的高为( )
A. 12+12 B. 24-24 C. 12-12 D. 24+24
5.已知,则x等于( )
A. 4 B. ±2 C. 2 D. ±4
6.若a、b、c为有理数,且等式成立,则2a+999b+1001c的值是( )
A. 1999 B. 2000 C. 2001 D. 不能确定
7.化简 结果正确的是( )
A. 3+2 B. 3- C. 17+12 D. 17-12
8.若3,m,5为三角形三边,化简: 得( ).
A. -10 B. -2m+6 C. -2m-6 D. 2m-10
9.观察下列等式:①=1+-=;②=1+-=;③.根据上面三个等式提供的信息,请猜想的结果为( )
A. B. C. D.
二、填空题
10.计算: =________
11.已知﹣=2,则的值为_____.
12.的整数部分是x,小数部分是y,则y(x+)的值为________ .
13.当x=2+时,式子x2﹣4x+2017=________.
14.对于任意实数a,b,定义一种运算“◇”如下:a◇b=a(a-b)+b(a+b),如:3◇2=3×(3-2)+2×(3+2)=13,那么◇=_____.
15.已知a、b、c是△ABC的三边,则的值为________.
16.不等式(1-)x>1+的最大整数解是________.
17.设a,b是有理数,且满足等式,则__________.
18.将一组数,2,,2,,…,2按图中的方法排列:
若3的位置记为(2,3),2的位置记为(3,2),则这组数中最大数的位置记为______.
三、解答题
19.计算:
(1)9÷×;
(2)( --)×(-2);
(3) ++-+;
(4)(3-)2(3+)+(3+)2(3-).
20.化简 .
21.一圆形转盘的面积是25.12cm2,该圆形转盘的半径是多少?(π取3.14)
22.已知: , ,求代数式的值.
23.若a,b为实数,且++>b,化简|2b-1|-.
24.先化简,再求值,其中a=,b=.
25.阅读下面问题:
;
;……
试求:(1)的值; (2)(n为正整数)的值;
(3)的值。
参考答案
1.C
【解析】A选项中, ,故A错误;
B选项中, ,故B错误;
C选项中, ,故C正确;
D选项中, ,故D错误;
∴选C.
2.C
【解析】=
,1.4<
所以3.1<。
故选C.
3.A
【解析】解:∵﹣2a<x<﹣a,a>x,∴x+a<0,x+2a>0,x﹣a<0,∴原式=﹣(x+a)+ +2(x+2a)=﹣x﹣a+2x+4a+|x﹣a|=x+3a+|x﹣a|=x+3a﹣x+a=4a.故选A.
点睛:解答此题,要弄清两个问题:(1)定义:一般地,形如(a≥0)的代数式叫做二次根式.当a>0时, 表示a的算术平方根,当a=0时, =0,当a小于0时,二次根式无意义;(2)性质: =|a|.
4.B
【解析】设高为h,根据题意得: (+1)h=12,
h===24-24,
故选:B.
5.C
【解析】试题解析:已知,
∴x>0,
∴原式可化简为: ,
∴,
两边平方得:2x=4,
∴x=2,
故选C.
6.B
【解析】因 =,所以a=0,b=1,c=1,即可得2a+999b+1001c=999+1001=2000,故选B.
点睛:本题考查了二次根式的性质与化简,将复合二次根式根据完全平方公式化简并比较系数是解题的关键.
7.A
【解析】试题解析: =.
故选A.
8.D
【解析】根据题意,得:2
∴原式=m 2+m 8=2m 10.故选D.
9.D
【解析】====,
故选:D.
点睛:本题属于探索规律型,主要考查学生的观察及学习能力,并根据观察总结规律的能力.
10.6
【解析】试题解析: 原式=(+2)×
=3×
=6.
故答案为6.
11.4
【解析】∵﹣=2,
∴(﹣)2=4,
∴x+=6,
∴(x+)2=36,
∴+=34,
∴=.
故答案为:4.
点睛:对于化简求值题,关键是要认真分析题目中的隐含条件,挖掘已知条件与结论之间的内在关系与联系,进行适当化简,再求值中要注意有关性质、公式、运算法则的灵活运用,在求值后还要注意检查.
12.1
【解析】分析:本题考查的是无理数的整数部分和小数部分的相关计算,小数部分要用原数减去整数部分.
解析:∵ 的整数部分是3,∴小数部分是: -3,∴x=3,y=-3,∴y(x+)= .
故答案为1.
13.2016
【解析】把所求的式子化成(x﹣2)2+2013然后代入式子计算,即可得到:x2﹣4x+2017=(x﹣2)2+2013 =()2+2013=3+2013=2016.
故答案是:2016.
点睛:此题主要考查了配方法的应用,解题关键是把式子配成完全平方,然后整体代入即可求解,考查了学生对整体思想的认识和应用,学生对整体思想不熟时出错的主要原因.
14.5
【解析】◇==5.
故本题应填5.
点睛:理解新定义运算的运算规则,其实就是一个对应关系,a对应,b对应,即将a=,b=,代入到代数式a(a-b)+b(a+b)中,再根据二次根式的混合运算法则进行计算,注意最终的结果一定要化为最简二次根式.
15.2c-2a
【解析】∵a,b,c分别是△ABC的三边,
∴a
∴=b+c a a b+c=2c 2a,
故答案为:2c-2a.
16.-4
【解析】不等式(1-)x>1+两边同乘以1+得:(1-3)x>4+2,
解得x<-2-,
∵-4<-2-3√<-3,
∴最大整数解是-4.
故答案为:-4.
17.1或
【解析】b=-5, ,
a=,
或者-11.
18.(17,6)
【解析】观察、分析这组数据可发现:第一个数是的积;第二个数是的积;第三个数是的积, 的积.
∵这组数据中最大的数:,
∴是这组数据中的第102个数.
∵每一行排列了6个数,而
∴是第17行第6个数,
∴这组数据中最大的一个数应记为(17,6).
点睛:(1)这组数据组中的第个数为;(2)该组数据是按从左到右,从小到大,每行6个数进行排列的;(3)的商是数据所在的行数,的余数是数据所在的列数.
19.(1) (2)2(3)-(4)42
【解析】试题分析:(1)利用二次根式的乘除运算法则计算.(2)先化成最简二次根式,再计算.(3) 先化成最简二次根式,再计算.(4)利用公式提取公因式,再求值.
试题解析:
(1)9÷×=9=3.
(2)( --)×(-2)==2.
(3) ++-+=+=.
(4)(3-)2(3+)+(3+)2(3-)=(3-)(3+)(3-)=(9-2)6=42.
20.
【解析】试题分析:括号内先进行约分运算,然后通分进行加减运算后进行乘法运算,最后与前面的式子通分进行加减运算即可得.
试题解析:原式=
=
=
= .
21.该圆形转盘的半径是2 cm.
【解析】试题分析:设该圆形转盘的半径是Rcm,根据圆的面积公式得出R.
解:设该圆形转盘的半径是Rcm,
根据题意得πR2=25.12,
∴R2=8,
∴R=2,
答:该圆形转盘的半径是2 cm.
22.
【解析】试题分析:由题意列二元一次方程组,分别求出x、y的值,再将x、y的值代入要求的式子即可.
试题解析:
由题意得: ,
解得,
∴==.
点睛:本题关键在于根据根式的性质列出方程组.
23.-b
【解析】试题解析:先由+成立,得a=1,所以b<,再根据负数的绝对值是它的相反数和=|a|进行化简.
试题解析:由题意得,
解得a=1,故b<,
∴2b-1<0,b-1<0,
∴|2b-1|-=1-2b-|b-1|=1-2b-(1-b)=-b.
24.,
【解析】试题分析:先根据分式混合运算的法则把原式进行化简,再把a、b的值代入进行计算即可.
试题解析:原式=
=
= ,
当a=,b=时,a+b==,
所以原式=.
点睛:本题考查了分式的化简求值:先把各分式的分子或分母因式分解,再进行分式的乘除运算,然后进行分式的加减运算得到最简分式或整式,再把满足条件的字母的值代入计算得到对应的分式的值;有括号先算括号.也考查了二次根式的计算.
25.(1)3-2;
(2)
(3)9
【解析】试题分析:根据题意给出的过程即可求出答案.
试题解析:解:(1)
(2)
(3)原式===10-1=9
点睛:本题考查分母有理化,解题的关键是熟练运用二次根式的性质,本题属于基础题型.
版权所有@21世纪教育网(www.21cnjy.com)
