17.2 勾股定理的逆定理同步练习
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
17.2勾股定理的逆定理同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
利用 勾股定理 在数轴上表示无理数,说明实数与数轴上的点是 一一对应的关系.
如果两个命题的题设、结论正好相反,我们把这样的两个命题叫做互逆命题,其中一个叫做原命题,另一个叫做它的逆命题 .
如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理互为逆定理.
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形 .
基础知识和能力拓展训练
一、选择题
1.已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )
A. 等边三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
2.三角形的三边长a,b,c满足2ab=(a+b)2﹣c2,则此三角形是( )
A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等边三角形
3.如图,在四边形,,,,,则四边形的面积是( ).
A. B. C. D. 无法确定
4.下列四组数:①3、4、5;② 、、;③0.3、0.4、0.5;④、、,其中是勾股数的有 ( )
A. 4组 B. 3组 C. 2组 D. 1组
5.如图,在由单位正方形组成的网格图标中有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的线段是( )
A. AB,CD,EF B. AB,CD,GH C. AB,EF,GH D. CD,EF,GH
6.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向,且到医院的距离为300m,公园到医院的距离为400m.若公园到超市的距离为500m,则公园在医院的( )
A. 北偏东75°的方向上 B. 北偏东65°的方向上
C. 北偏东55°的方向上 D. 无法确定
7.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A. B. C. D.
8.在如图所示的网格中,每个小正方形的边长都为1,△ABC的顶点都在格点上,三边长分别为a、b、c,则a、b、c的大小关系是( )
A. a二、填空题
9.如图,在四边形ABCD中,AB,BC,CD,DA的长分别为2,2,2,2,且AB⊥BC,则∠BAD的度数等于____.
10.李老师要做一个直角三角形教具,做好后量得三边长分别是30cm,40cm,和50cm,则这个教具______________(填“合格”或“不合格”).
11.已知三角形三边长分别是6,8,10,则此三角形的面积为______.
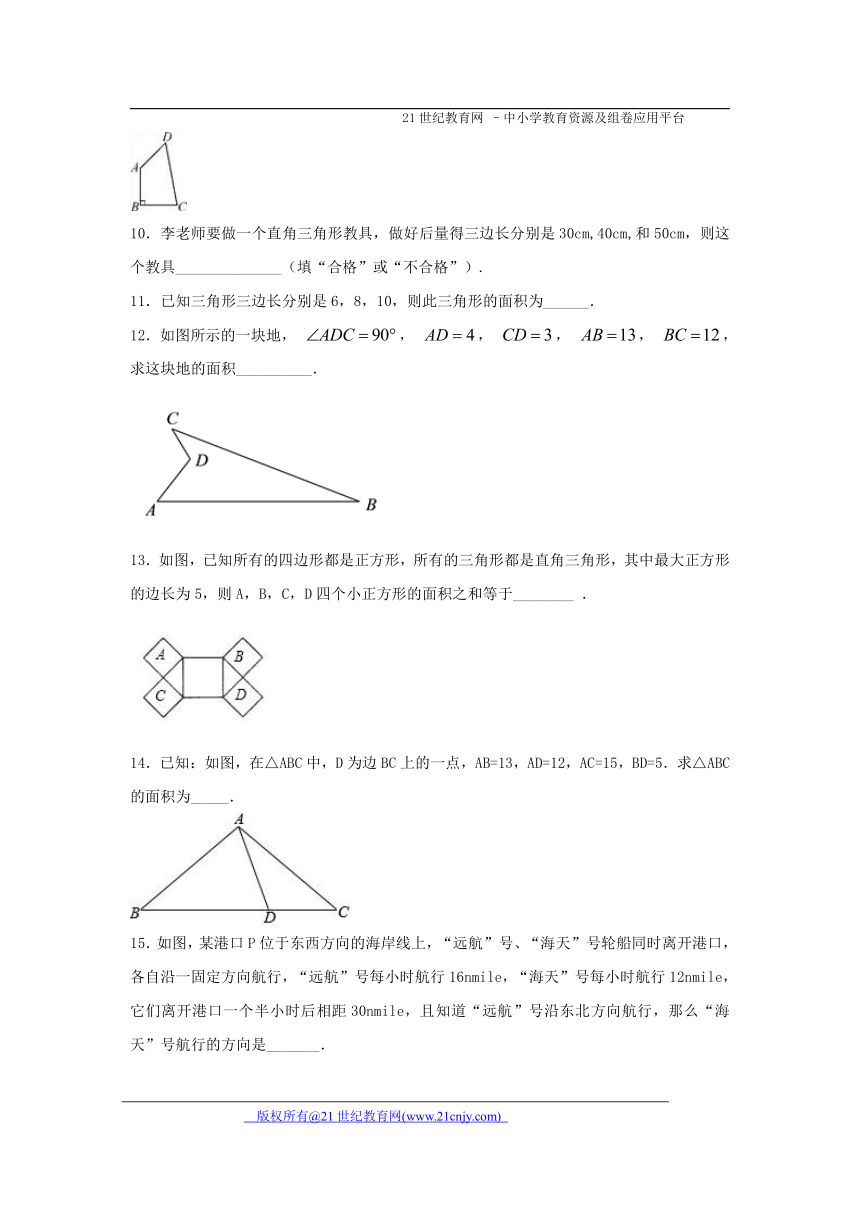
12.如图所示的一块地, , , , , ,求这块地的面积__________.
13.如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5,则A,B,C,D四个小正方形的面积之和等于________ .
14.已知:如图,在△ABC中,D为边BC上的一点,AB=13,AD=12,AC=15,BD=5.求△ABC的面积为_____.
15.如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16nmile,“海天”号每小时航行12nmile,它们离开港口一个半小时后相距30nmile,且知道“远航”号沿东北方向航行,那么“海天”号航行的方向是_______.
三、解答题
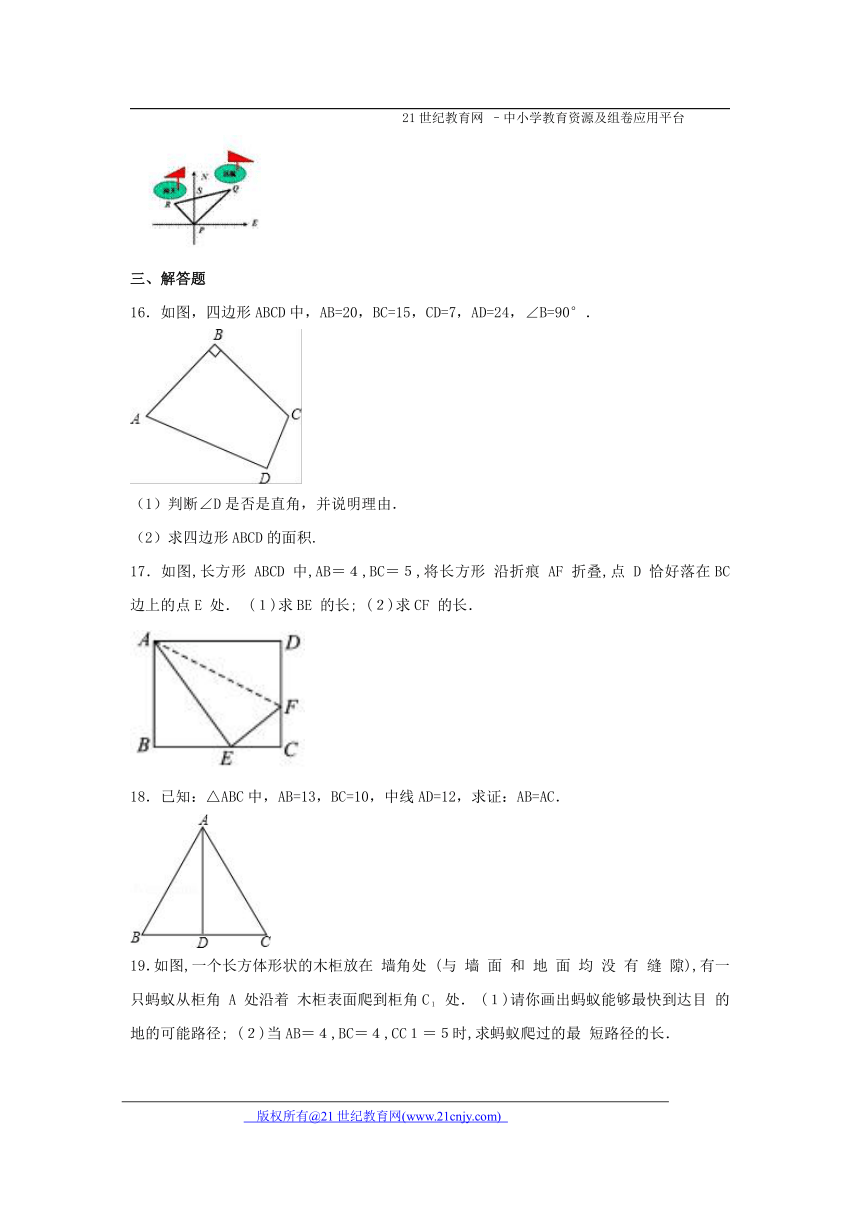
16.如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
17.如图,长方形 ABCD 中,AB=4,BC=5,将长方形 沿折痕 AF 折叠,点 D 恰好落在BC 边上的点E 处. (1)求BE 的长; (2)求CF 的长.
18.已知:△ABC中,AB=13,BC=10,中线AD=12,求证:AB=AC.
19.如图,一个长方体形状的木柜放在 墙角处 (与 墙 面 和 地 面 均 没 有 缝 隙),有一只蚂蚁从柜角 A 处沿着 木柜表面爬到柜角C1 处. (1)请你画出蚂蚁能够最快到达目 的地的可能路径; (2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最 短路径的长.
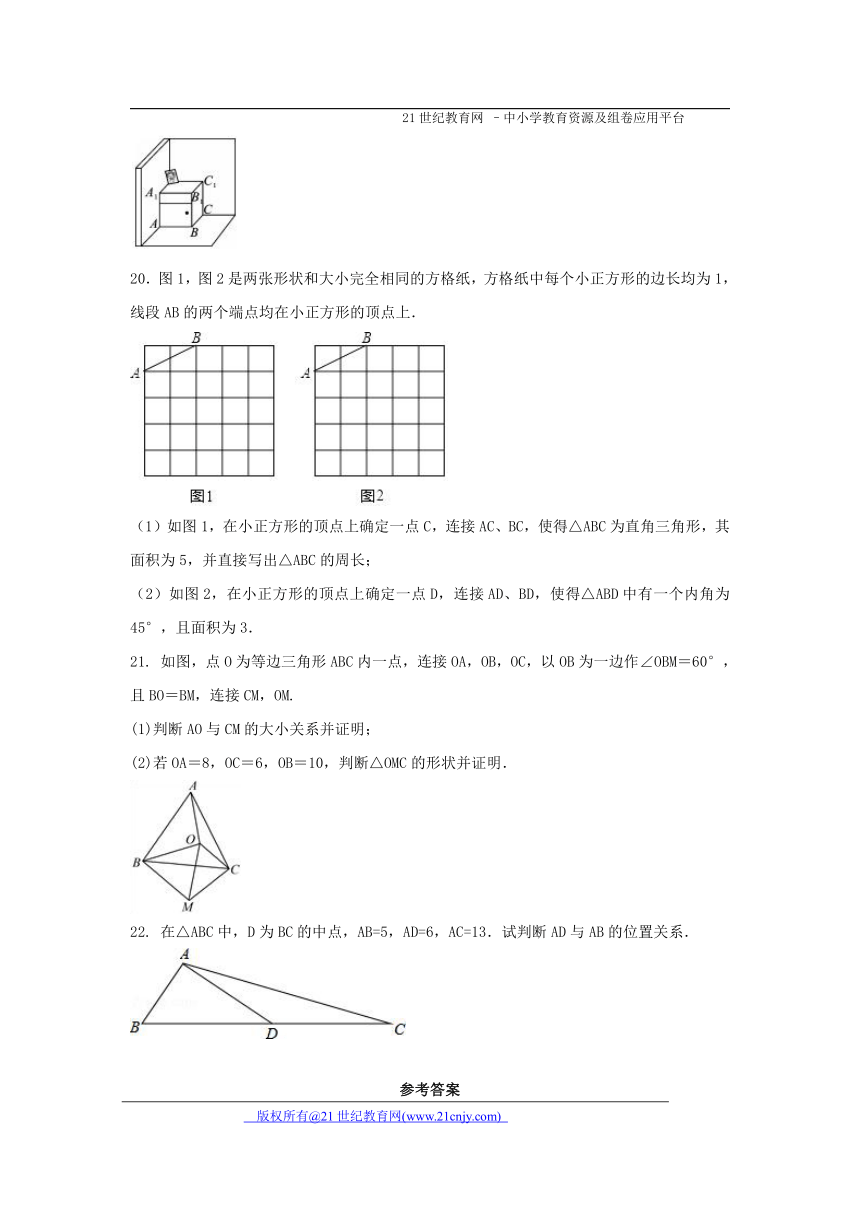
20.图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3.
21. 如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
22. 在△ABC中,D为BC的中点,AB=5,AD=6,AC=13.试判断AD与AB的位置关系.
参考答案
1.D
【解析】∵(a b)(a +b c )=0,
∴a b=0,或a +b c =0,
即a=b或a +b =c ,
∴△ABC的形状为等腰三角形或直角三角形。
故选:D.
2.C
【解析】∵原式可化为a2+b2=c2 ,
∴此三角形是直角三角形,
故选C.
3.B
【解析】
连接BD,
∵∠A=90°,AD=AB=4,
∴BD==4,
∵CD=2,BC=6,
∴BD2+CD2=BC2,
∴∠CDB=90°,
∴S四边形ABCD=S△ABD+S△BCD=×4×4+×4×2=8+4.
故选B.
点睛:若三角形三边之间的关系满足两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
4.D
【解析】解:∵勾股数是正整数,∴②③④都不是勾股数,∵32+42=52.∴①是勾股数,故选D.
5.C
【解析】由勾股定理知,EF=,AB=,CD=, ,
5+8=13, ,所以由勾股定理逆定理AB,EF,GH可以构成直角三角形.
所以选C.
点睛:
勾股定理:在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方.这个定理叫毕达哥拉斯定理,最早由毕达哥拉斯证明,中国商代发现了勾三股四弦五,仅仅是一个特例,严格讲不能叫定理.
设直角三角形两直角边为a和b,斜边为c,有 a2 + b2 = c2 .
勾股定理逆定理:如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.最长边所对的角为直角.
设三角形三边有 a2 + b2 = c2 . 则∠C=90°.
6.B
【解析】试题解析:如图,
∵3002+4002=5002,
∴∠AOB=90°,
∵超市在医院的南偏东25°的方向,
∴∠COB=90°-25°=65°,
∴∠AOC=90°-65°=25°,
∴∠AOD=90°-25°=65°.
故选B.
7.A
【解析】如图,BC==,所以OA=OB+BC=1+,所以a=-1-,故选A
8.C
【解析】根据勾股定理可得: , , ,即可得c9.135°
【解析】试题分析:连接AC.
∵AB⊥BC于B,
∴∠B=90°,
在Rt△ABC中,
∴AB2+BC2=AC2,
又∵AB=CB=2,
∴AC=,∠BAC=∠BCA=45°,
∵CD=,DA=2,
∴DA2+AC2=4+8=12,CD2=12,
∴DA2+AC2=CD2,
由勾股定理的逆定理得:∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=45°+90°=135°.
故答案为135.
点睛:本题考查了根据勾股定理逆定理判定直角三角形及勾股定理在直角三角形中的运用,本题中求证△ACD是直角三角形是解题的关键.
10.合格
【解析】因,根据勾股定理的逆定理可得这个三角形为直角三角形,故答案为合格.
11.24.
【解析】试题解析:
此三角形为直角三角形,
此三角形的面积为:
故答案为:
12.
【解析】连接,
∵, , .
∴
.
∵.
∴.
∴.
∴
.
13.50
【解析】试题解析:∵所有的三角形都是直角三角形,
∴正方形A和C的面积和就是大正方形的面积,
同理,正方形B和D的面积和等于大正方形的面积,
∴四个小正方形的面积=2×5×5=50.
故答案为:50.
14.84
【解析】∵AB=13,AD=12,BD=5,
∴AB2=169,AD2=144,BD2=25,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴∠ADC=90°,
∴DC=,
∴BC=BD+DC=5+9=14,
∴S△ABC=BC·AD=.
15.西北方向
【解析】根据路程=速度×时间分别求得PQ、PR的长,再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形,从而求解.
解:根据题意,得
PQ=16×1.5=24(海里),PR=12×1.5=18(海里),QR=30(海里).
∵242+182=302,
即PQ2+PR2=QR2,
∴∠QPR=90°.
由“远航号”沿东北方向航行可知,∠QPS=45°,则∠SPR=45°,
即“海天”号沿西北方向航行.
“点睛”此题主要是能够根据勾股定理的逆定理发现直角三角形.
16.(1)∠D是直角(2)234
【解析】试题分析:(1)∠D是直角,连接AC.首先根据勾股定理求得AC的长,再根据勾股定理的逆定理求得∠D=90°即可;
(2)由题意可知四边形ABCD的面积等于两个直角三角形的面积问题的解.
试题解析:解:(1)∠D是直角.理由如下:
连接AC.∵AB=20,BC=15,∠B=90°,∴由勾股定理得AC2=202+152=625.
又∵CD=7,AD=24,∴CD2十AD2=625,∴AC2=CD2+AD2,∴∠D=90°,∴AD与CD垂直;
(2)四边形ABCD的面积=AD DC+AB BC=×24×7+×20×15=234.
点睛:考查了勾股定理和勾股定理的逆定理,通过作辅助线可将一般的四边形转化为两个直角三角形,使面积的求解过程变得简单.
17.解:(1)由题意得:AE=AD=BC =5,EF=DF.在 Rt△ABE 中, BE== =3.
(2)∵BC=5,BE=3, ∴CE=2.
设CF=x,则DF=4-x,
∴EF=4-x,在Rt△CEF中,
∵EF2=CE2+CF2,
∴(4-x)2=22+x2,
解得x= ,即CF= .
18.见解析
【解析】试题分析:
由勾股定理的逆定理判断△ABD是直角三角形,再根据线段垂直平分线的性质即可得证.
试题解析:
∵AD是△ABC的中线,BC=10,∴BD=DC=BC=5.
∵BD2+AD2=52+122=132=AB2,∴AD⊥BC,
∵AD是△ABC的BC边的中线,
∴AD是BC的中垂线,
∴AB=AC.
19.解:(1)如 图,木 柜 的 表 面 展 开 图 是 两 个 矩 形 ABC1′D1 和ACC1A1.蚂蚁能够最快到达目的 地的可能路径有如图所示的 AC1′和AC1 两 种.
(2)蚂蚁沿着木柜表面经线段A1B1到C1′,爬过的路径的长l1= 42+(4+5)2=97.
蚂蚁 沿着木柜表面经线段 BB1到C1,爬过的路径的长l2=(4+4)2+52= 89.
∵l1>l2,∴最短路径的长是 89.
20.(1)5+3;(2)3.
【解析】试题分析:(1)构造直角三角形,AB=且是直角边,面积是5,可以求出另外一条直角边BC长度,最后连接AC.
(2)先构造一个45°角,再利用面积是3,可画出图象.
试题解析:
(1)解:如图1所示:△ABC即为所求,
△ABC的周长为: +2+5=5+3;
(2)解:如图2所示:△ABD中,∠ADB=45°,且面积为3.
21. (1)AO=CM (2)△OMC是直角三角形
【解析】试题分析:(1)先证明△OBM是等边三角形,得出OM=OB,∠ABC=∠OBC,由SAS证明△AOB≌△CMB,即可得出结论;
(2)由勾股定理的逆定理即可得出结论.
试题解析:解:(1)AO=CM.理由如下:
∵∠OBM=60°,OB=BM,∴△OBM是等边三角形,∴OM=OB=10,∠ABC=∠OBC=60°,
∴∠ABO=∠CBM.在△AOB和△CMB中,∵OB=OM,∠ABO=∠CBM,AB=BC,∴△AOB≌△CMB(SAS),∴OA=MC;
(2)△OMC是直角三角形;理由如下:
在△OMC中,OM2=100,OC2+CM2=62+82=100,∴OM2=OC2+CM2,∴△OMC是直角三角形.
点睛:本题考查了等边三角形的判定与性质、全等三角形的判定与性质、勾股定理的逆定理.证明三角形全等是解决问题的关键.
22. AD⊥AB,理由见解析
【解析】试题分析:
延长AD至E,使得AD=DE,连接BE,则易证△ADC≌△EDB(SAS),得EB=AC,在△ABE中由勾股定理的逆定理判断△ABE是直角三角形.
试题解析:
延长AD至E,使得AD=DE,连接BE,
∵D为BC的中点,∴BD=CD,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),∴EB=AC=13,
∵AD=6,∴AE=12,
∵52+122=132,∴AB2+AE2=EB2,
∴∠BAE=90°,
∴AD⊥AB.
版权所有@21世纪教育网(www.21cnjy.com)
17.2勾股定理的逆定理同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
利用 勾股定理 在数轴上表示无理数,说明实数与数轴上的点是 一一对应的关系.
如果两个命题的题设、结论正好相反,我们把这样的两个命题叫做互逆命题,其中一个叫做原命题,另一个叫做它的逆命题 .
如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理互为逆定理.
如果三角形的三边长a、b、c满足a2+b2=c2,那么这个三角形是直角三角形 .
基础知识和能力拓展训练
一、选择题
1.已知a、b、c为△ABC的三边,且满足(a﹣b)(a2+b2﹣c2)=0,则△ABC是( )
A. 等边三角形 B. 直角三角形
C. 等腰直角三角形 D. 等腰三角形或直角三角形
2.三角形的三边长a,b,c满足2ab=(a+b)2﹣c2,则此三角形是( )
A. 钝角三角形 B. 锐角三角形 C. 直角三角形 D. 等边三角形
3.如图,在四边形,,,,,则四边形的面积是( ).
A. B. C. D. 无法确定
4.下列四组数:①3、4、5;② 、、;③0.3、0.4、0.5;④、、,其中是勾股数的有 ( )
A. 4组 B. 3组 C. 2组 D. 1组
5.如图,在由单位正方形组成的网格图标中有AB,CD,EF,GH四条线段,其中能构成一个直角三角形三边的线段是( )
A. AB,CD,EF B. AB,CD,GH C. AB,EF,GH D. CD,EF,GH
6.如图是医院、公园和超市的平面示意图,超市在医院的南偏东25°的方向,且到医院的距离为300m,公园到医院的距离为400m.若公园到超市的距离为500m,则公园在医院的( )
A. 北偏东75°的方向上 B. 北偏东65°的方向上
C. 北偏东55°的方向上 D. 无法确定
7.如图所示,在数轴上点A所表示的数为a,则a的值为( )
A. B. C. D.
8.在如图所示的网格中,每个小正方形的边长都为1,△ABC的顶点都在格点上,三边长分别为a、b、c,则a、b、c的大小关系是( )
A. a
9.如图,在四边形ABCD中,AB,BC,CD,DA的长分别为2,2,2,2,且AB⊥BC,则∠BAD的度数等于____.
10.李老师要做一个直角三角形教具,做好后量得三边长分别是30cm,40cm,和50cm,则这个教具______________(填“合格”或“不合格”).
11.已知三角形三边长分别是6,8,10,则此三角形的面积为______.
12.如图所示的一块地, , , , , ,求这块地的面积__________.
13.如图,已知所有的四边形都是正方形,所有的三角形都是直角三角形,其中最大正方形的边长为5,则A,B,C,D四个小正方形的面积之和等于________ .
14.已知:如图,在△ABC中,D为边BC上的一点,AB=13,AD=12,AC=15,BD=5.求△ABC的面积为_____.
15.如图,某港口P位于东西方向的海岸线上,“远航”号、“海天”号轮船同时离开港口,各自沿一固定方向航行,“远航”号每小时航行16nmile,“海天”号每小时航行12nmile,它们离开港口一个半小时后相距30nmile,且知道“远航”号沿东北方向航行,那么“海天”号航行的方向是_______.
三、解答题
16.如图,四边形ABCD中,AB=20,BC=15,CD=7,AD=24,∠B=90°.
(1)判断∠D是否是直角,并说明理由.
(2)求四边形ABCD的面积.
17.如图,长方形 ABCD 中,AB=4,BC=5,将长方形 沿折痕 AF 折叠,点 D 恰好落在BC 边上的点E 处. (1)求BE 的长; (2)求CF 的长.
18.已知:△ABC中,AB=13,BC=10,中线AD=12,求证:AB=AC.
19.如图,一个长方体形状的木柜放在 墙角处 (与 墙 面 和 地 面 均 没 有 缝 隙),有一只蚂蚁从柜角 A 处沿着 木柜表面爬到柜角C1 处. (1)请你画出蚂蚁能够最快到达目 的地的可能路径; (2)当AB=4,BC=4,CC1=5时,求蚂蚁爬过的最 短路径的长.
20.图1,图2是两张形状和大小完全相同的方格纸,方格纸中每个小正方形的边长均为1,线段AB的两个端点均在小正方形的顶点上.
(1)如图1,在小正方形的顶点上确定一点C,连接AC、BC,使得△ABC为直角三角形,其面积为5,并直接写出△ABC的周长;
(2)如图2,在小正方形的顶点上确定一点D,连接AD、BD,使得△ABD中有一个内角为45°,且面积为3.
21. 如图,点O为等边三角形ABC内一点,连接OA,OB,OC,以OB为一边作∠OBM=60°,且BO=BM,连接CM,OM.
(1)判断AO与CM的大小关系并证明;
(2)若OA=8,OC=6,OB=10,判断△OMC的形状并证明.
22. 在△ABC中,D为BC的中点,AB=5,AD=6,AC=13.试判断AD与AB的位置关系.
参考答案
1.D
【解析】∵(a b)(a +b c )=0,
∴a b=0,或a +b c =0,
即a=b或a +b =c ,
∴△ABC的形状为等腰三角形或直角三角形。
故选:D.
2.C
【解析】∵原式可化为a2+b2=c2 ,
∴此三角形是直角三角形,
故选C.
3.B
【解析】
连接BD,
∵∠A=90°,AD=AB=4,
∴BD==4,
∵CD=2,BC=6,
∴BD2+CD2=BC2,
∴∠CDB=90°,
∴S四边形ABCD=S△ABD+S△BCD=×4×4+×4×2=8+4.
故选B.
点睛:若三角形三边之间的关系满足两边的平方和等于第三边的平方,那么这个三角形是直角三角形.
4.D
【解析】解:∵勾股数是正整数,∴②③④都不是勾股数,∵32+42=52.∴①是勾股数,故选D.
5.C
【解析】由勾股定理知,EF=,AB=,CD=, ,
5+8=13, ,所以由勾股定理逆定理AB,EF,GH可以构成直角三角形.
所以选C.
点睛:
勾股定理:在任何一个直角三角形中,两条直角边的平方之和一定等于斜边的平方.这个定理叫毕达哥拉斯定理,最早由毕达哥拉斯证明,中国商代发现了勾三股四弦五,仅仅是一个特例,严格讲不能叫定理.
设直角三角形两直角边为a和b,斜边为c,有 a2 + b2 = c2 .
勾股定理逆定理:如果三角形两条边的平方和等于第三边的平方,那么这个三角形就是直角三角形.最长边所对的角为直角.
设三角形三边有 a2 + b2 = c2 . 则∠C=90°.
6.B
【解析】试题解析:如图,
∵3002+4002=5002,
∴∠AOB=90°,
∵超市在医院的南偏东25°的方向,
∴∠COB=90°-25°=65°,
∴∠AOC=90°-65°=25°,
∴∠AOD=90°-25°=65°.
故选B.
7.A
【解析】如图,BC==,所以OA=OB+BC=1+,所以a=-1-,故选A
8.C
【解析】根据勾股定理可得: , , ,即可得c
【解析】试题分析:连接AC.
∵AB⊥BC于B,
∴∠B=90°,
在Rt△ABC中,
∴AB2+BC2=AC2,
又∵AB=CB=2,
∴AC=,∠BAC=∠BCA=45°,
∵CD=,DA=2,
∴DA2+AC2=4+8=12,CD2=12,
∴DA2+AC2=CD2,
由勾股定理的逆定理得:∠DAC=90°,
∴∠BAD=∠BAC+∠DAC=45°+90°=135°.
故答案为135.
点睛:本题考查了根据勾股定理逆定理判定直角三角形及勾股定理在直角三角形中的运用,本题中求证△ACD是直角三角形是解题的关键.
10.合格
【解析】因,根据勾股定理的逆定理可得这个三角形为直角三角形,故答案为合格.
11.24.
【解析】试题解析:
此三角形为直角三角形,
此三角形的面积为:
故答案为:
12.
【解析】连接,
∵, , .
∴
.
∵.
∴.
∴.
∴
.
13.50
【解析】试题解析:∵所有的三角形都是直角三角形,
∴正方形A和C的面积和就是大正方形的面积,
同理,正方形B和D的面积和等于大正方形的面积,
∴四个小正方形的面积=2×5×5=50.
故答案为:50.
14.84
【解析】∵AB=13,AD=12,BD=5,
∴AB2=169,AD2=144,BD2=25,
∴AD2+BD2=AB2,
∴∠ADB=90°,
∴∠ADC=90°,
∴DC=,
∴BC=BD+DC=5+9=14,
∴S△ABC=BC·AD=.
15.西北方向
【解析】根据路程=速度×时间分别求得PQ、PR的长,再进一步根据勾股定理的逆定理可以证明三角形PQR是直角三角形,从而求解.
解:根据题意,得
PQ=16×1.5=24(海里),PR=12×1.5=18(海里),QR=30(海里).
∵242+182=302,
即PQ2+PR2=QR2,
∴∠QPR=90°.
由“远航号”沿东北方向航行可知,∠QPS=45°,则∠SPR=45°,
即“海天”号沿西北方向航行.
“点睛”此题主要是能够根据勾股定理的逆定理发现直角三角形.
16.(1)∠D是直角(2)234
【解析】试题分析:(1)∠D是直角,连接AC.首先根据勾股定理求得AC的长,再根据勾股定理的逆定理求得∠D=90°即可;
(2)由题意可知四边形ABCD的面积等于两个直角三角形的面积问题的解.
试题解析:解:(1)∠D是直角.理由如下:
连接AC.∵AB=20,BC=15,∠B=90°,∴由勾股定理得AC2=202+152=625.
又∵CD=7,AD=24,∴CD2十AD2=625,∴AC2=CD2+AD2,∴∠D=90°,∴AD与CD垂直;
(2)四边形ABCD的面积=AD DC+AB BC=×24×7+×20×15=234.
点睛:考查了勾股定理和勾股定理的逆定理,通过作辅助线可将一般的四边形转化为两个直角三角形,使面积的求解过程变得简单.
17.解:(1)由题意得:AE=AD=BC =5,EF=DF.在 Rt△ABE 中, BE== =3.
(2)∵BC=5,BE=3, ∴CE=2.
设CF=x,则DF=4-x,
∴EF=4-x,在Rt△CEF中,
∵EF2=CE2+CF2,
∴(4-x)2=22+x2,
解得x= ,即CF= .
18.见解析
【解析】试题分析:
由勾股定理的逆定理判断△ABD是直角三角形,再根据线段垂直平分线的性质即可得证.
试题解析:
∵AD是△ABC的中线,BC=10,∴BD=DC=BC=5.
∵BD2+AD2=52+122=132=AB2,∴AD⊥BC,
∵AD是△ABC的BC边的中线,
∴AD是BC的中垂线,
∴AB=AC.
19.解:(1)如 图,木 柜 的 表 面 展 开 图 是 两 个 矩 形 ABC1′D1 和ACC1A1.蚂蚁能够最快到达目的 地的可能路径有如图所示的 AC1′和AC1 两 种.
(2)蚂蚁沿着木柜表面经线段A1B1到C1′,爬过的路径的长l1= 42+(4+5)2=97.
蚂蚁 沿着木柜表面经线段 BB1到C1,爬过的路径的长l2=(4+4)2+52= 89.
∵l1>l2,∴最短路径的长是 89.
20.(1)5+3;(2)3.
【解析】试题分析:(1)构造直角三角形,AB=且是直角边,面积是5,可以求出另外一条直角边BC长度,最后连接AC.
(2)先构造一个45°角,再利用面积是3,可画出图象.
试题解析:
(1)解:如图1所示:△ABC即为所求,
△ABC的周长为: +2+5=5+3;
(2)解:如图2所示:△ABD中,∠ADB=45°,且面积为3.
21. (1)AO=CM (2)△OMC是直角三角形
【解析】试题分析:(1)先证明△OBM是等边三角形,得出OM=OB,∠ABC=∠OBC,由SAS证明△AOB≌△CMB,即可得出结论;
(2)由勾股定理的逆定理即可得出结论.
试题解析:解:(1)AO=CM.理由如下:
∵∠OBM=60°,OB=BM,∴△OBM是等边三角形,∴OM=OB=10,∠ABC=∠OBC=60°,
∴∠ABO=∠CBM.在△AOB和△CMB中,∵OB=OM,∠ABO=∠CBM,AB=BC,∴△AOB≌△CMB(SAS),∴OA=MC;
(2)△OMC是直角三角形;理由如下:
在△OMC中,OM2=100,OC2+CM2=62+82=100,∴OM2=OC2+CM2,∴△OMC是直角三角形.
点睛:本题考查了等边三角形的判定与性质、全等三角形的判定与性质、勾股定理的逆定理.证明三角形全等是解决问题的关键.
22. AD⊥AB,理由见解析
【解析】试题分析:
延长AD至E,使得AD=DE,连接BE,则易证△ADC≌△EDB(SAS),得EB=AC,在△ABE中由勾股定理的逆定理判断△ABE是直角三角形.
试题解析:
延长AD至E,使得AD=DE,连接BE,
∵D为BC的中点,∴BD=CD,
在△ADC和△EDB中,
,
∴△ADC≌△EDB(SAS),∴EB=AC=13,
∵AD=6,∴AE=12,
∵52+122=132,∴AB2+AE2=EB2,
∴∠BAE=90°,
∴AD⊥AB.
版权所有@21世纪教育网(www.21cnjy.com)
