数学六年级下人教版6.4数学思考课件(20张)
文档属性
| 名称 | 数学六年级下人教版6.4数学思考课件(20张) |

|
|
| 格式 | zip | ||
| 文件大小 | 451.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版(新课程标准) | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-03 00:00:00 | ||
图片预览








文档简介
课件20张PPT。第6单元 整理和复习
4.数学思考
第9节 数学思考
第1课时 数学思考(1)
在小学阶段的数学课堂中我们学习了许多有趣的数学趣题,你还记得吗?
1. 鸡兔同笼;2.烙饼问题;3.抽屉原理……
还记得我们是如何解决这些数学问题的吗?一、回忆数学思想方法,揭示课题1. 数形结合;2.列举;3.假设;4.化繁为简……
这些数学思想和方法可以帮助我们有条理地思考,简捷地去解决问题。
二、探究学习例1 请你认真审题,尝试独立解决这个问题。然后和组内的同学说一说你是如何解决的。例1 6个点可以连多少条线段?8个点呢? 方法:
(1)运用数形结合的思想,先画图,再数线段的条数。
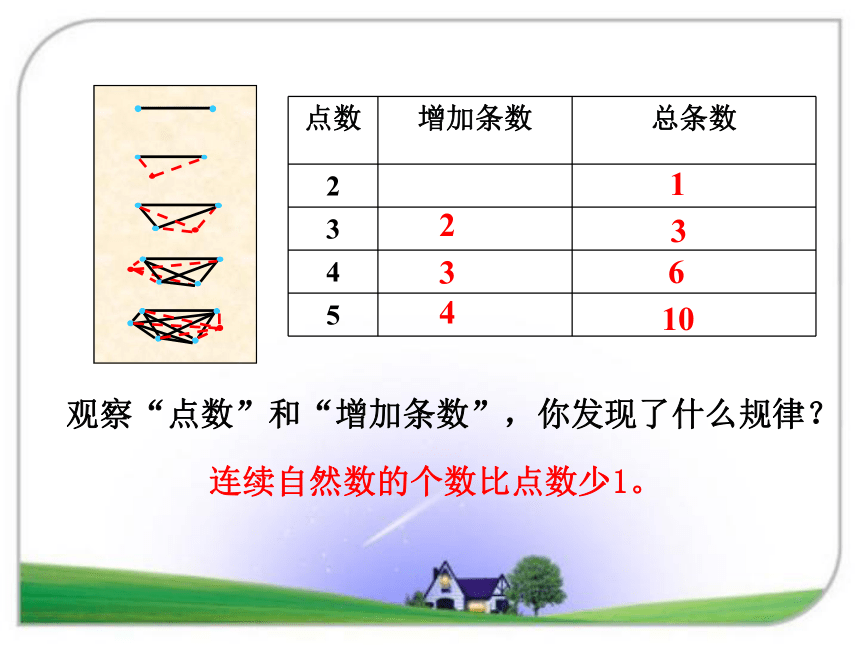
(2)运用化繁为简的思想,先从两点连成一条直线开始,逐渐发现规律。例1 6个点可以连多少条线段?8个点呢?观察“点数”和“增加条数”,你发现了什么规律?
连续自然数的个数比点数少1。 12336410 根据规律,你知道6个点、10个点、20个点能连成多少条线段吗?6个点:1+2+3+4+5=15(条)10个点:1+2+3+4+5+6+7+8+9
=(1+9)+(2+8)+(3+7)+(4+6)+5
=45(条) 根据规律,你知道6个点、10个点、20个点能连成多少条线段吗?20个点:1+2+3+4+5+6+7+8+9+10+11+
12+13+14+15+16+17+18+19
= (1+19)+ (2+18)+ (3+17)+…+ ( 8+12)
+ ( 9+11)+10
=190(条) n个点能连成线段的条数又该怎样表示呢? 因为连续自然数的个数比点数少1,比n少1的数即是(n-1),所以n个点连成的线段条数就是从1开始前(n-1)个连续自然数的和,即1+2+3+…+(n-1)。 另一种方法:n(n-1)÷2 1.足球邀请赛赛制如下:日本、中国、美国、英国、加拿大每两个球队进行一场比赛,一共要踢几场球?基本练习: 5×(5-1)÷2=10(场)
答:一共要踢10场球。 2.每两人握1次手,4个同学一共要握几次手?(学生相互握手)全班同学又该握几次呢?用哪种方法能快速解决这一问题?4×(4-1)÷2=6(次)
答:4个同学一共要握6次手。 例2 六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?三、探究学习例2汇报:你能得到哪些信息?用“/” 表示到会,用“○”表示没到会。 六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?(1)从第一次到会的情况,你可以看出什么?
A只可能和D、E或F同班。 (2)从第二次到会的情况,你可以判断出什么?
A只可能和D、E同班。 (3)从第三次到会的情况,你可以判断出什么?
A只可能和D同班那么B和C分别与谁同班? A和D同班,在剩下的B、C、E、F中,从第一次到会的情况可以看出,B只能和E或F同班;从第二次到会的情况可以看出,B只能和F同班。所以C只可能与E同班。 王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。请问:他们的职业各是什么?问题:你想用什么方法解决这个问题?××√√√√ 这节课我们复习了数学思考。学会了用观察、探究、记录、归纳、列表等方法解决数学实际问题,并且能运用一定规律解决较复杂的数学问题,感受到数学思想方法的重要性,从中体会到了数学的乐趣。四、全课总结这节课我们复习了什么?你有什么收获? 我们的数学源于生活又用于生活,生活中处处都可以发现数学和数学的美,所以希望每位同学喜欢数学、爱数学,我相信在以后的生活中,我们一定会有更神奇的发现,希望每位同学加油!谢谢大家!
再见!
4.数学思考
第9节 数学思考
第1课时 数学思考(1)
在小学阶段的数学课堂中我们学习了许多有趣的数学趣题,你还记得吗?
1. 鸡兔同笼;2.烙饼问题;3.抽屉原理……
还记得我们是如何解决这些数学问题的吗?一、回忆数学思想方法,揭示课题1. 数形结合;2.列举;3.假设;4.化繁为简……
这些数学思想和方法可以帮助我们有条理地思考,简捷地去解决问题。
二、探究学习例1 请你认真审题,尝试独立解决这个问题。然后和组内的同学说一说你是如何解决的。例1 6个点可以连多少条线段?8个点呢? 方法:
(1)运用数形结合的思想,先画图,再数线段的条数。
(2)运用化繁为简的思想,先从两点连成一条直线开始,逐渐发现规律。例1 6个点可以连多少条线段?8个点呢?观察“点数”和“增加条数”,你发现了什么规律?
连续自然数的个数比点数少1。 12336410 根据规律,你知道6个点、10个点、20个点能连成多少条线段吗?6个点:1+2+3+4+5=15(条)10个点:1+2+3+4+5+6+7+8+9
=(1+9)+(2+8)+(3+7)+(4+6)+5
=45(条) 根据规律,你知道6个点、10个点、20个点能连成多少条线段吗?20个点:1+2+3+4+5+6+7+8+9+10+11+
12+13+14+15+16+17+18+19
= (1+19)+ (2+18)+ (3+17)+…+ ( 8+12)
+ ( 9+11)+10
=190(条) n个点能连成线段的条数又该怎样表示呢? 因为连续自然数的个数比点数少1,比n少1的数即是(n-1),所以n个点连成的线段条数就是从1开始前(n-1)个连续自然数的和,即1+2+3+…+(n-1)。 另一种方法:n(n-1)÷2 1.足球邀请赛赛制如下:日本、中国、美国、英国、加拿大每两个球队进行一场比赛,一共要踢几场球?基本练习: 5×(5-1)÷2=10(场)
答:一共要踢10场球。 2.每两人握1次手,4个同学一共要握几次手?(学生相互握手)全班同学又该握几次呢?用哪种方法能快速解决这一问题?4×(4-1)÷2=6(次)
答:4个同学一共要握6次手。 例2 六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?三、探究学习例2汇报:你能得到哪些信息?用“/” 表示到会,用“○”表示没到会。 六年级有三个班,每班有2个班长。开班长会时,每次每班只要一个班长参加。第一次到会的有A、B、C;第二次有B、D、E;第三次有A、E、F。请问:哪两位班长是同班的?(1)从第一次到会的情况,你可以看出什么?
A只可能和D、E或F同班。 (2)从第二次到会的情况,你可以判断出什么?
A只可能和D、E同班。 (3)从第三次到会的情况,你可以判断出什么?
A只可能和D同班那么B和C分别与谁同班? A和D同班,在剩下的B、C、E、F中,从第一次到会的情况可以看出,B只能和E或F同班;从第二次到会的情况可以看出,B只能和F同班。所以C只可能与E同班。 王阿姨、刘阿姨、丁叔叔、李叔叔分别是工人、教师、军人。王阿姨是教师;丁叔叔不是工人;只有刘阿姨和李叔叔的职业相同。请问:他们的职业各是什么?问题:你想用什么方法解决这个问题?××√√√√ 这节课我们复习了数学思考。学会了用观察、探究、记录、归纳、列表等方法解决数学实际问题,并且能运用一定规律解决较复杂的数学问题,感受到数学思想方法的重要性,从中体会到了数学的乐趣。四、全课总结这节课我们复习了什么?你有什么收获? 我们的数学源于生活又用于生活,生活中处处都可以发现数学和数学的美,所以希望每位同学喜欢数学、爱数学,我相信在以后的生活中,我们一定会有更神奇的发现,希望每位同学加油!谢谢大家!
再见!
