6.3.2 实数(课件)
图片预览











文档简介
(共50张PPT)
6.3实数(2)
人教版 七年级下
有理数
实数
无理数
正有理数
0
负有理数
有限小数
或无限循环小数
有理数和无理数统称实数。
正无理数
负无理数
无限不循环小数
小练习:把下列各数分别填入相应的集合内
有理数集合
无理数集合
…
…
π
π
0
0.3737737773······
0
0.3737737773···
每个有理数都可以用数轴上的点来表示。
无理数是否也可以用数轴上的点来表示呢?
我们还知道
【问题1】 探究 π 在数轴上的表示
探究 2
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O/,点O/的坐标是多少?
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O/,点O/对应的数是多少?
0123
C=π
π
O/
点O/对应的数是 π
因此,无理数 π 可以用数轴上的点表示出来。
边长是1的正方形的对角线的长是
我们已经知道:
1
1
1
1
x
1
x
S大正方形=x2=2
1
【问题2】 探究 在数轴上如何表示?
和 也可以用数轴上的点表示出来。
【问题2】 探究 在数轴上如何表示?
-2 -1 0 1 2
事实上,每一个无理数都可以用数轴上的一个点表示出来。即数轴上的点有些是有理数,有些是无理数。
当数从有理数扩充到实数以后,实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示实数。
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大。
当我们将数的范围扩大之后,在实数范围内:相反数、倒数、绝对值的意义和有理范围内的相反数、倒数、绝对值的意义完全相同。
思考题
⑴ 的相反数是 .
-π的相反数是 .
0 的相反数是 .
π
0
⑴ 的相反数是 .
-π的相反数是 .
0 的相反数是 .
π
0
⑵ 的相反数是 .
的相反数是 .
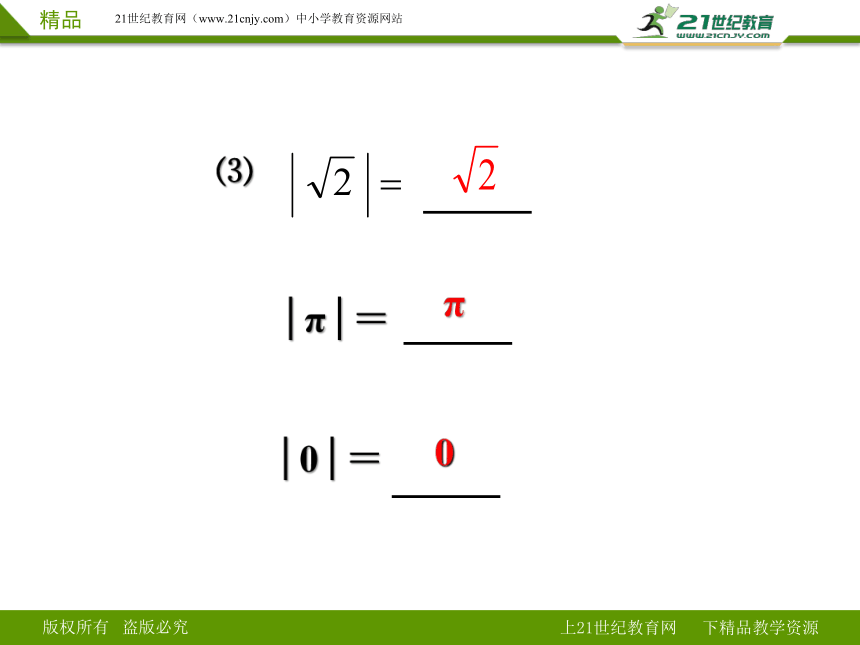
⑶
π
│π│=
│0│=
0
⑴ a是实数,它的相反数为 ,
它的绝对值为 ;
⑵ 如果a≠0,那么它的倒数为 ;
-a
│a│
填一填
关于绝对值的意义
⑴ 一个正实数的绝对值是它本身;
⑵ 一个负实数的绝对值是它的相反数;
⑶ 0的绝对值是0;
│a│=a ( a>0)
│a│=-a ( a<0)
│a│=
-a ( a<0)
a ( a>0)
0 ( a=0)
一个正实数的绝对值是它本身;
一个负实数的绝对值是它的相反数;
0的绝对值是0;
关于绝对值的意义
例1、填空题
⑴ 的相反数是 ;
⑵ π-3.14的相反数是 ;
⑶ 的绝对值是 ;
⑷ 若│x│= ,则 x= 。
3.14-π
4
当数从有理数扩充到实数以后,实数之间不仅可以进行加、减、乘、除(除数不为0)、乘方运算,而且正数及0可以进行开平方运算,任意一个实数可以进行开立方运算。在进行实数运算时,有理数的运算法则及运算性质同样适用。
例2、计算下列各式的值。
⑴
⑵
解:⑴ 原式=
⑵ 原式=
例3、计算(结果保留小数点后两位)
⑴
⑵
解:⑴ 原式≈2.236+3.142
≈5.38
⑵ 原式≈1.732×1.414
≈2.45
1、请将图中数轴上标有字母的各点与下列实数对应起来:
,-1.5, ,π,3
-3 -2 -1 0 1 2 3 4
A
B
C
DE
解:A对应-1.5,
B对应
C对应
D对应 3
E对应 π.
2.5, , , , 0。
2、求下列各数的相反数与绝对值:
解:2.5的相反数是-2.5;
的相反数是
的相反数是
│2.5│=2.5
的相反数是
0的相反数是0
2.5, , , , 0。
2、求下列各数的相反数与绝对值:
│0│=0
3、求下列各式中的实数 x (共4道小题)
⑴
⑵│x│=0
解:⑴
⑵
x=0
⑶
⑷│x│=π
⑶
⑷
x=±π
3、求下列各式中的实数 x (共4道小题)
4、计算(共5道题)
⑴
解:⑴ 原式=
⑵
解:原式=
4、计算(共5道题)
⑶
⑶ 原式=
4、计算(共5道题)
⑷
⑷ 原式=
4、计算(共5道题)
⑸
解:⑸原式=-8+3+2
=-3
4、计算(共5道题)
5、计算(共5道小题)
⑴
解:⑴ 原式=
⑵
⑵ 原式=
5、计算(共5道小题)
⑶
⑶ 原式=
⑷
⑷ 原式=
=3+1
=4
5、计算(共5道小题)
⑸
⑸ 原式=
5、计算(共5道小题)
非负数的应用专题训练
6、已知a,b,c,满足
则a= ,b= ,c= 。
3
4
解:∵
∴ a-3=0, b-4=0, c- =0
解,得 a=3, b=4, c=
7、已知数x,y满足:
则(x+y)2018= .
1
∴ x+5=0
y-4=0
x=-5
y=4
(x+y)2018=(-1)2018 =1
非负数的应用专题训练
解:∵
8、若式子 有意义,
则x的取值范围是【 】
(A) x≥ (B) ≤x≤1
(B) x≤1 (D)以上答案都不对
A
解:4x-1≥0
x≥
9、已知 y= ,求 的值。
解:由题意可得
x-3≥0
x≥3
3-x≥0
x≤3
x=3
y=0+0+9=9
=3
10、已知 y= ,求xy的值。
解:由题意可得
2x-1≥0
x≥0.5
1-2x≥0
x≤0.5
x=0.5
y=0+0+2=2
xy=
0.52=0.25
11、已知: ,求 yx 的平方根.
解:由题意可得
解,得 x=2
∴
y=9
yx 的平方根为
12、若
求 x+y+z 的立方根。
解:∵
∴ x-2011 =0
y+2012 =0
z+7=0
即 x=2011
y=-2012
z=-7
x+y+z=
2011-2012-7
=-8
=-2
13、已知 a 和 x 是有理数,且有:
则 x = .
只能取a=0
3x-5=4
3
解,得 x=3
14、已知实数a满足:
求a-20172的值。
解:由题意,可知
a-2018≥0
∴ a≥2018
因此,有:
a-2018=20172
∴ a-20172= 2018
15、已知 x+8 的算术平方根是3,y-5的立方根是2,
试求 的值。
解:由题意,可知
x+8=32
y-5=23
x=1
y=13
=-2
16、如图所示,数轴上表示1、 的对应点分别是
A、B,点B关于A的对称点为C,则点C表示
的数是 。
C
B
A
O
1
?
17、如图所示,数轴上表示3、 的点分别为点C、
B,且C是AB的中点,则点A表示的数是【 】
A
B
C
O
3
(A)
(B)
(C)
(D)
B
18、若 求 的平方根。
解:由题意,得
x-1=0
y-2=0
x=1
y=2
3
的平方根为:
19、求x的值 (共2道题)
⑴ 4x2=25 ⑵ (x-0.7)3=0.027
解:⑴
⑵
x-0.7=0.3
x=1
20、已知某数有两个平方根分别是a+3与2a-15,
求这个数。
(a+3)+(2a-15)=0
解:由题意,得
解,得
a=4
a+3=7
这个数是:
(a+3)2=72=49
21、实数a、b在数轴上的位置如图所示:化简
a 0 b
解:原式=
│a│-│b│+│a-b│
=-a-b-(a-b)
=-a-b-a+b
=-2a
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
6.3实数(2)
人教版 七年级下
有理数
实数
无理数
正有理数
0
负有理数
有限小数
或无限循环小数
有理数和无理数统称实数。
正无理数
负无理数
无限不循环小数
小练习:把下列各数分别填入相应的集合内
有理数集合
无理数集合
…
…
π
π
0
0.3737737773······
0
0.3737737773···
每个有理数都可以用数轴上的点来表示。
无理数是否也可以用数轴上的点来表示呢?
我们还知道
【问题1】 探究 π 在数轴上的表示
探究 2
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O/,点O/的坐标是多少?
如图,直径为1个单位长度的圆从原点沿数轴向右滚动一周,圆上的一点由原点到达点O/,点O/对应的数是多少?
0123
C=π
π
O/
点O/对应的数是 π
因此,无理数 π 可以用数轴上的点表示出来。
边长是1的正方形的对角线的长是
我们已经知道:
1
1
1
1
x
1
x
S大正方形=x2=2
1
【问题2】 探究 在数轴上如何表示?
和 也可以用数轴上的点表示出来。
【问题2】 探究 在数轴上如何表示?
-2 -1 0 1 2
事实上,每一个无理数都可以用数轴上的一个点表示出来。即数轴上的点有些是有理数,有些是无理数。
当数从有理数扩充到实数以后,实数与数轴上的点就是一一对应的,即每一个实数都可以用数轴上的一个点来表示;反过来,数轴上的每一个点都表示实数。
与规定有理数的大小一样,对于数轴上的任意两个点,右边的点表示的实数总比左边的点表示的实数大。
当我们将数的范围扩大之后,在实数范围内:相反数、倒数、绝对值的意义和有理范围内的相反数、倒数、绝对值的意义完全相同。
思考题
⑴ 的相反数是 .
-π的相反数是 .
0 的相反数是 .
π
0
⑴ 的相反数是 .
-π的相反数是 .
0 的相反数是 .
π
0
⑵ 的相反数是 .
的相反数是 .
⑶
π
│π│=
│0│=
0
⑴ a是实数,它的相反数为 ,
它的绝对值为 ;
⑵ 如果a≠0,那么它的倒数为 ;
-a
│a│
填一填
关于绝对值的意义
⑴ 一个正实数的绝对值是它本身;
⑵ 一个负实数的绝对值是它的相反数;
⑶ 0的绝对值是0;
│a│=a ( a>0)
│a│=-a ( a<0)
│a│=
-a ( a<0)
a ( a>0)
0 ( a=0)
一个正实数的绝对值是它本身;
一个负实数的绝对值是它的相反数;
0的绝对值是0;
关于绝对值的意义
例1、填空题
⑴ 的相反数是 ;
⑵ π-3.14的相反数是 ;
⑶ 的绝对值是 ;
⑷ 若│x│= ,则 x= 。
3.14-π
4
当数从有理数扩充到实数以后,实数之间不仅可以进行加、减、乘、除(除数不为0)、乘方运算,而且正数及0可以进行开平方运算,任意一个实数可以进行开立方运算。在进行实数运算时,有理数的运算法则及运算性质同样适用。
例2、计算下列各式的值。
⑴
⑵
解:⑴ 原式=
⑵ 原式=
例3、计算(结果保留小数点后两位)
⑴
⑵
解:⑴ 原式≈2.236+3.142
≈5.38
⑵ 原式≈1.732×1.414
≈2.45
1、请将图中数轴上标有字母的各点与下列实数对应起来:
,-1.5, ,π,3
-3 -2 -1 0 1 2 3 4
A
B
C
DE
解:A对应-1.5,
B对应
C对应
D对应 3
E对应 π.
2.5, , , , 0。
2、求下列各数的相反数与绝对值:
解:2.5的相反数是-2.5;
的相反数是
的相反数是
│2.5│=2.5
的相反数是
0的相反数是0
2.5, , , , 0。
2、求下列各数的相反数与绝对值:
│0│=0
3、求下列各式中的实数 x (共4道小题)
⑴
⑵│x│=0
解:⑴
⑵
x=0
⑶
⑷│x│=π
⑶
⑷
x=±π
3、求下列各式中的实数 x (共4道小题)
4、计算(共5道题)
⑴
解:⑴ 原式=
⑵
解:原式=
4、计算(共5道题)
⑶
⑶ 原式=
4、计算(共5道题)
⑷
⑷ 原式=
4、计算(共5道题)
⑸
解:⑸原式=-8+3+2
=-3
4、计算(共5道题)
5、计算(共5道小题)
⑴
解:⑴ 原式=
⑵
⑵ 原式=
5、计算(共5道小题)
⑶
⑶ 原式=
⑷
⑷ 原式=
=3+1
=4
5、计算(共5道小题)
⑸
⑸ 原式=
5、计算(共5道小题)
非负数的应用专题训练
6、已知a,b,c,满足
则a= ,b= ,c= 。
3
4
解:∵
∴ a-3=0, b-4=0, c- =0
解,得 a=3, b=4, c=
7、已知数x,y满足:
则(x+y)2018= .
1
∴ x+5=0
y-4=0
x=-5
y=4
(x+y)2018=(-1)2018 =1
非负数的应用专题训练
解:∵
8、若式子 有意义,
则x的取值范围是【 】
(A) x≥ (B) ≤x≤1
(B) x≤1 (D)以上答案都不对
A
解:4x-1≥0
x≥
9、已知 y= ,求 的值。
解:由题意可得
x-3≥0
x≥3
3-x≥0
x≤3
x=3
y=0+0+9=9
=3
10、已知 y= ,求xy的值。
解:由题意可得
2x-1≥0
x≥0.5
1-2x≥0
x≤0.5
x=0.5
y=0+0+2=2
xy=
0.52=0.25
11、已知: ,求 yx 的平方根.
解:由题意可得
解,得 x=2
∴
y=9
yx 的平方根为
12、若
求 x+y+z 的立方根。
解:∵
∴ x-2011 =0
y+2012 =0
z+7=0
即 x=2011
y=-2012
z=-7
x+y+z=
2011-2012-7
=-8
=-2
13、已知 a 和 x 是有理数,且有:
则 x = .
只能取a=0
3x-5=4
3
解,得 x=3
14、已知实数a满足:
求a-20172的值。
解:由题意,可知
a-2018≥0
∴ a≥2018
因此,有:
a-2018=20172
∴ a-20172= 2018
15、已知 x+8 的算术平方根是3,y-5的立方根是2,
试求 的值。
解:由题意,可知
x+8=32
y-5=23
x=1
y=13
=-2
16、如图所示,数轴上表示1、 的对应点分别是
A、B,点B关于A的对称点为C,则点C表示
的数是 。
C
B
A
O
1
?
17、如图所示,数轴上表示3、 的点分别为点C、
B,且C是AB的中点,则点A表示的数是【 】
A
B
C
O
3
(A)
(B)
(C)
(D)
B
18、若 求 的平方根。
解:由题意,得
x-1=0
y-2=0
x=1
y=2
3
的平方根为:
19、求x的值 (共2道题)
⑴ 4x2=25 ⑵ (x-0.7)3=0.027
解:⑴
⑵
x-0.7=0.3
x=1
20、已知某数有两个平方根分别是a+3与2a-15,
求这个数。
(a+3)+(2a-15)=0
解:由题意,得
解,得
a=4
a+3=7
这个数是:
(a+3)2=72=49
21、实数a、b在数轴上的位置如图所示:化简
a 0 b
解:原式=
│a│-│b│+│a-b│
=-a-b-(a-b)
=-a-b-a+b
=-2a
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
