7.1.2平面直角坐标系(课件)
图片预览




文档简介
(共23张PPT)
7.1.2平面直角坐标系
人教版 七年级下
大量确定位置的需要,早在17世纪初,法国数学家笛卡尔受到了经纬度的启发,他利用平面内互相垂直的两条数轴,来准确地确定平面内点的位置,由此,使一门新兴的数学(解析几何)诞生了。
一、平面直角坐标系的历史
二、从数轴到平面直角坐标系
如图,是一条数轴,数轴上的点与实数是一一对应的,数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标。
-5 -4 -3 -2 -1 0 1 2 3 4 5
例如:点A在数轴上的坐标为 。
A
-4
点B在数轴上的坐标为 。
B
2
二、从数轴到平面直角坐标系
-5 -4 -3 -2 -1 0 1 2 3 4 5
例如:点A在数轴上的坐标为 。
A
-4
点B在数轴上的坐标为 。
B
2
数轴上坐标为 5 的点是点 。
C
C
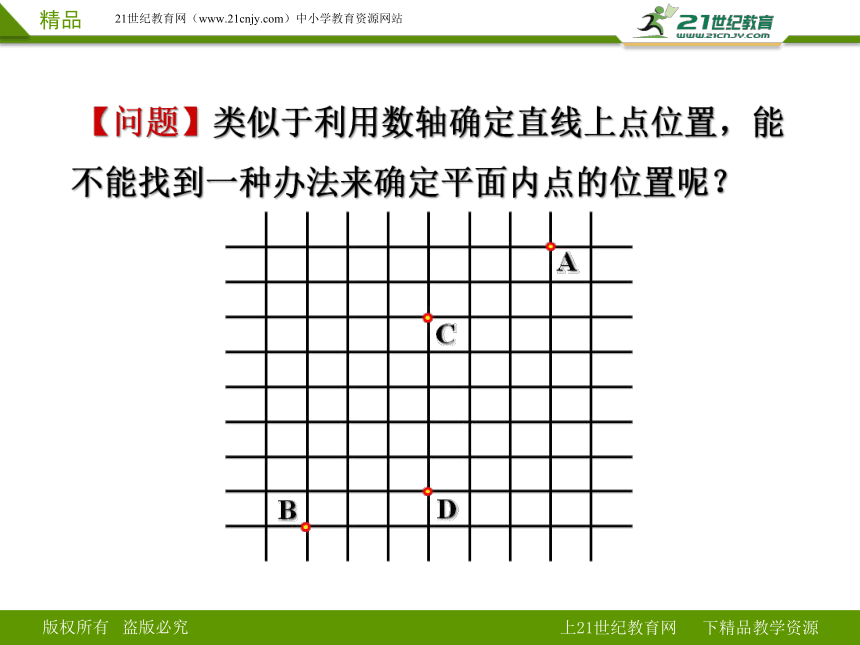
【问题】类似于利用数轴确定直线上点位置,能不能找到一种办法来确定平面内的点的位置呢?
【问题】类似于利用数轴确定直线上点位置,能不能找到一种办法来确定平面内点的位置呢?
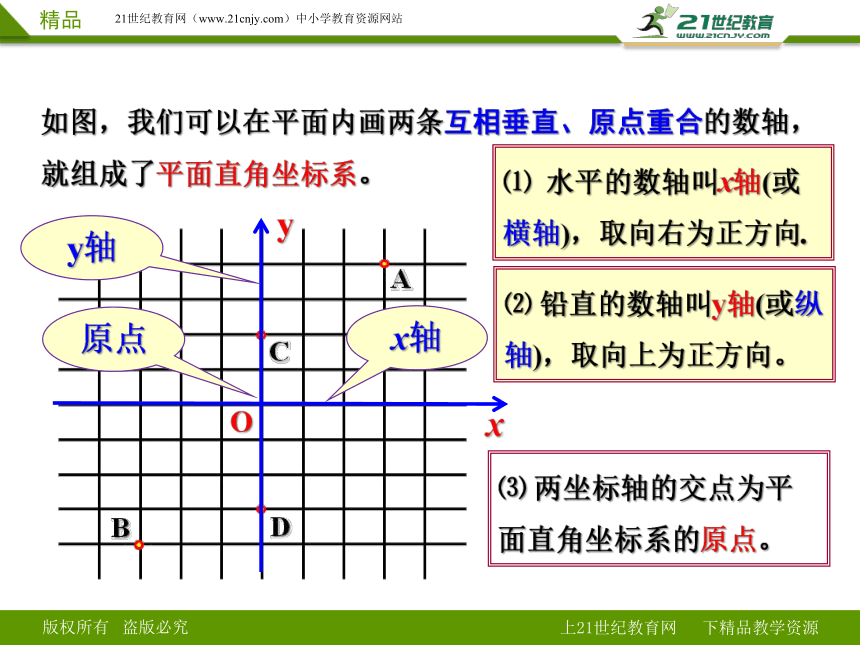
如图,我们可以在平面内画两条互相垂直、原点重合的数轴,就组成了平面直角坐标系。
x
y
O
x轴
y轴
⑴ 水平的数轴叫x轴(或横轴),取向右为正方向.
⑵ 铅直的数轴叫y轴(或纵轴),取向上为正方向。
⑶ 两坐标轴的交点为平面直角坐标系的原点。
原点
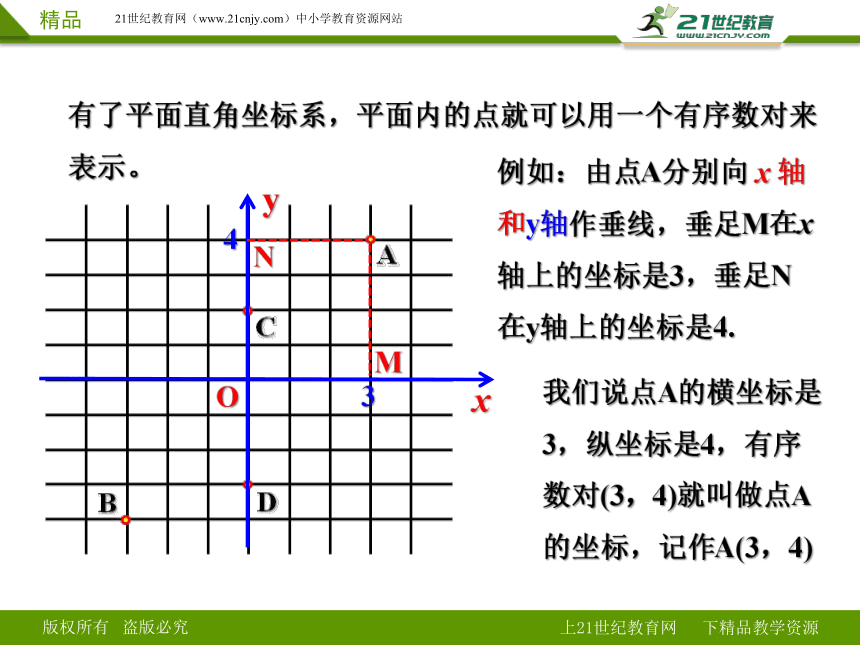
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示。
x
y
O
例如:由点A分别向 x 轴和y轴作垂线,垂足M在x轴上的坐标是3,垂足N在y轴上的坐标是4.
我们说点A的横坐标是3,纵坐标是4,有序数对(3,4)就叫做点A的坐标,记作A(3,4)
M
N
4
3
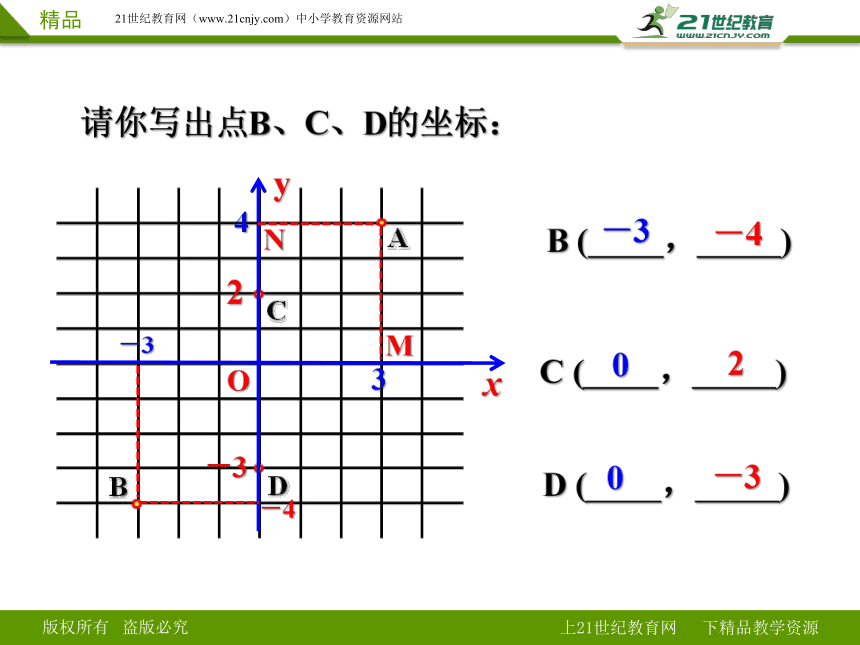
请你写出点B、C、D的坐标:
x
y
O
B ( , )
M
N
4
3
-3
-4
C ( , )
D ( , )
-3
-4
0
2
0
-3
2
-3
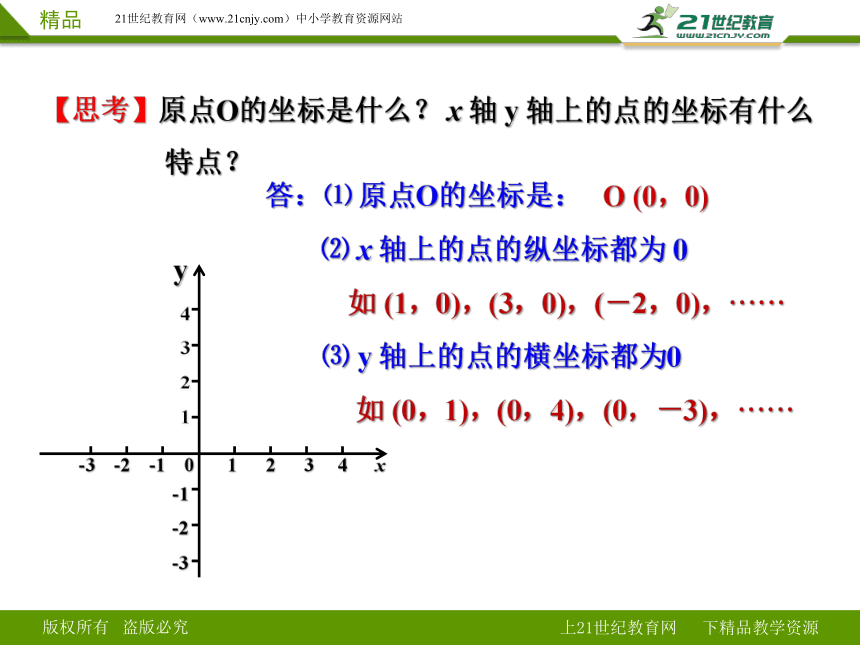
【思考】原点O的坐标是什么? x 轴 y 轴上的点的坐标有什么
特点?
-3 -2 -1 0 1 2 3 4 x
4
3
2
1
-1
-2
-3
y
答:⑴ 原点O的坐标是:
⑵ x 轴上的点的纵坐标都为 0
O (0,0)
⑶ y 轴上的点的横坐标都为0
如 (1,0),(3,0),(-2,0),······
如 (0,1),(0,4),(0,-3),······
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限、第四象限。
-3 -2 -1 0 1 2 3 4 x
4
3
2
1
-1
-2
-3
y
第一象限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限。
平面直角坐标系,
两条数轴作标记。
作垂线,定垂足,
找出对应的实数.
先横后纵再括号,
中间必须用逗号。
欣赏与理解
-3 -2 -1 0 1 2 3 4 x
4
3
2
1
-1
-2
-3
y
A(3,4)
第一象限
第二象限
第三象限
第四象限
【例1】 在平面直角坐标系中,描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4)
A
E
B
C
D
【例2】 写出A、B、C、D、E各点的坐标。
A
E
B
C
D
解:A( 2,3 )
B( 3,2 )
C( -2,1 )
D( -4,-3 )
E( 1,-2 )
【例3】写出如图所示的六边形ABCDEF各个顶点的坐标。
解:A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
E
D
C
B
A
F
x
y
O
1
1
E
D
C
B
A
F
x
y
O
1
1
【例4】⑴ 线段BC的位置有什么特点?
⑵ 线段CE的位置有什么特点?
答:⑴ 线段BC∥x轴.
⑵ 线段EC∥y轴.
点的位置 横坐标符号 纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
【例5】如图,建立平面直角坐标系,使点B,C的坐标分别为(0,0)和(4,0),写出点A,D,E,F,G的坐标,并指出它们所在的象限。
A
B
C
D
E
F
G
x
y
o
(0,0)
答:⑴A
(-2,3)
⑵B
(4,0)
⑶C
(6,1)
⑷D
(5,3)
⑸E
(3,2)
⑹F
(1,5)
⑺G
〖拓展练习〗
例6、过A(0,0),B(2,2)两点画直线.
B(2,2)
A
●
x
y
0
2
2
1
1
-1
-2
-1
-2
●
解:
【例7】顺次连接三点A(-1,-1),B(2,-1)
C(2,5) 得到了什么图形?
3
1
4
2
5
-2
-1
0
1
2
3
4
5
-4
-3
-2
-1
x
y
●
A
B
●
C
●
答:得到直角三角形ABC.
【例8】在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限:
⑴ 点P(x,y)的坐标满足 xy>0;
解:⑴ ∵ xy>0
∴ x>0,y>0 或 x<0,y<0
例如: A(2,3), B(-5,-1)
答: 这些点在第一象限或第三象限。
【例8】在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限:
⑵ 点P(x,y)的坐标满足 xy<0.
解:⑵ ∵ xy<0
∴ x>0,y<0 或 x<0,y>0
例如: C(2,-3), D(-6,4)
答: 这些点在第二象限或第四象限。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
7.1.2平面直角坐标系
人教版 七年级下
大量确定位置的需要,早在17世纪初,法国数学家笛卡尔受到了经纬度的启发,他利用平面内互相垂直的两条数轴,来准确地确定平面内点的位置,由此,使一门新兴的数学(解析几何)诞生了。
一、平面直角坐标系的历史
二、从数轴到平面直角坐标系
如图,是一条数轴,数轴上的点与实数是一一对应的,数轴上每个点都对应一个实数,这个实数叫做这个点在数轴上的坐标。
-5 -4 -3 -2 -1 0 1 2 3 4 5
例如:点A在数轴上的坐标为 。
A
-4
点B在数轴上的坐标为 。
B
2
二、从数轴到平面直角坐标系
-5 -4 -3 -2 -1 0 1 2 3 4 5
例如:点A在数轴上的坐标为 。
A
-4
点B在数轴上的坐标为 。
B
2
数轴上坐标为 5 的点是点 。
C
C
【问题】类似于利用数轴确定直线上点位置,能不能找到一种办法来确定平面内的点的位置呢?
【问题】类似于利用数轴确定直线上点位置,能不能找到一种办法来确定平面内点的位置呢?
如图,我们可以在平面内画两条互相垂直、原点重合的数轴,就组成了平面直角坐标系。
x
y
O
x轴
y轴
⑴ 水平的数轴叫x轴(或横轴),取向右为正方向.
⑵ 铅直的数轴叫y轴(或纵轴),取向上为正方向。
⑶ 两坐标轴的交点为平面直角坐标系的原点。
原点
有了平面直角坐标系,平面内的点就可以用一个有序数对来表示。
x
y
O
例如:由点A分别向 x 轴和y轴作垂线,垂足M在x轴上的坐标是3,垂足N在y轴上的坐标是4.
我们说点A的横坐标是3,纵坐标是4,有序数对(3,4)就叫做点A的坐标,记作A(3,4)
M
N
4
3
请你写出点B、C、D的坐标:
x
y
O
B ( , )
M
N
4
3
-3
-4
C ( , )
D ( , )
-3
-4
0
2
0
-3
2
-3
【思考】原点O的坐标是什么? x 轴 y 轴上的点的坐标有什么
特点?
-3 -2 -1 0 1 2 3 4 x
4
3
2
1
-1
-2
-3
y
答:⑴ 原点O的坐标是:
⑵ x 轴上的点的纵坐标都为 0
O (0,0)
⑶ y 轴上的点的横坐标都为0
如 (1,0),(3,0),(-2,0),······
如 (0,1),(0,4),(0,-3),······
建立了平面直角坐标系以后,坐标平面就被两条坐标轴分成Ⅰ、Ⅱ、Ⅲ、Ⅳ四个部分,每个部分称为象限,分别叫做第一象限、第二象限、第三象限、第四象限。
-3 -2 -1 0 1 2 3 4 x
4
3
2
1
-1
-2
-3
y
第一象限
Ⅰ
Ⅱ
Ⅲ
Ⅳ
第二象限
第三象限
第四象限
注意:坐标轴上的点不属于任何象限。
平面直角坐标系,
两条数轴作标记。
作垂线,定垂足,
找出对应的实数.
先横后纵再括号,
中间必须用逗号。
欣赏与理解
-3 -2 -1 0 1 2 3 4 x
4
3
2
1
-1
-2
-3
y
A(3,4)
第一象限
第二象限
第三象限
第四象限
【例1】 在平面直角坐标系中,描出下列各点:
A(4,5),B(-2,3),C(-4,-1),D(2.5,-2),E(0,-4)
A
E
B
C
D
【例2】 写出A、B、C、D、E各点的坐标。
A
E
B
C
D
解:A( 2,3 )
B( 3,2 )
C( -2,1 )
D( -4,-3 )
E( 1,-2 )
【例3】写出如图所示的六边形ABCDEF各个顶点的坐标。
解:A(-2,0)
B(0,-3)
C(3,-3)
D(4,0)
E(3,3)
F(0,3)
E
D
C
B
A
F
x
y
O
1
1
E
D
C
B
A
F
x
y
O
1
1
【例4】⑴ 线段BC的位置有什么特点?
⑵ 线段CE的位置有什么特点?
答:⑴ 线段BC∥x轴.
⑵ 线段EC∥y轴.
点的位置 横坐标符号 纵坐标符号
在第一象限
在第二象限
在第三象限
在第四象限
在x轴上 在正半轴上
在负半轴上
在y轴上 在正半轴上
在负半轴上
原点
【例5】如图,建立平面直角坐标系,使点B,C的坐标分别为(0,0)和(4,0),写出点A,D,E,F,G的坐标,并指出它们所在的象限。
A
B
C
D
E
F
G
x
y
o
(0,0)
答:⑴A
(-2,3)
⑵B
(4,0)
⑶C
(6,1)
⑷D
(5,3)
⑸E
(3,2)
⑹F
(1,5)
⑺G
〖拓展练习〗
例6、过A(0,0),B(2,2)两点画直线.
B(2,2)
A
●
x
y
0
2
2
1
1
-1
-2
-1
-2
●
解:
【例7】顺次连接三点A(-1,-1),B(2,-1)
C(2,5) 得到了什么图形?
3
1
4
2
5
-2
-1
0
1
2
3
4
5
-4
-3
-2
-1
x
y
●
A
B
●
C
●
答:得到直角三角形ABC.
【例8】在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限:
⑴ 点P(x,y)的坐标满足 xy>0;
解:⑴ ∵ xy>0
∴ x>0,y>0 或 x<0,y<0
例如: A(2,3), B(-5,-1)
答: 这些点在第一象限或第三象限。
【例8】在平面直角坐标系中选择一些横、纵坐标满足下面条件的点,标出它们的位置,看看它们在第几象限:
⑵ 点P(x,y)的坐标满足 xy<0.
解:⑵ ∵ xy<0
∴ x>0,y<0 或 x<0,y>0
例如: C(2,-3), D(-6,4)
答: 这些点在第二象限或第四象限。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
