7.2.2用坐标表示平移(课件)
图片预览





文档简介
(共20张PPT)
7.2.2用坐标表示
平移
人教版 七年级下
在平面直角坐标系中,对一个图形进行平移,图形上的点的位置发生了变化,坐标也一定会发生变化。
但是,平移过程中,坐标的变化规律是怎样呢?下面我们就通过具体例题来进行探究,从中发现其中的规律。
【例1】如图,将点A(-2,-3)向右平移5个单位长度,
得到点A1 ,⑴ 在图上标出这个点,并写出它的坐标。
●
(-2,-3)
A
x
y
0
A1
A(-2,-3)
A1(3,-3)
向右平移5个单位
(3,-3)
横坐标加5,纵坐标不变
-2
3
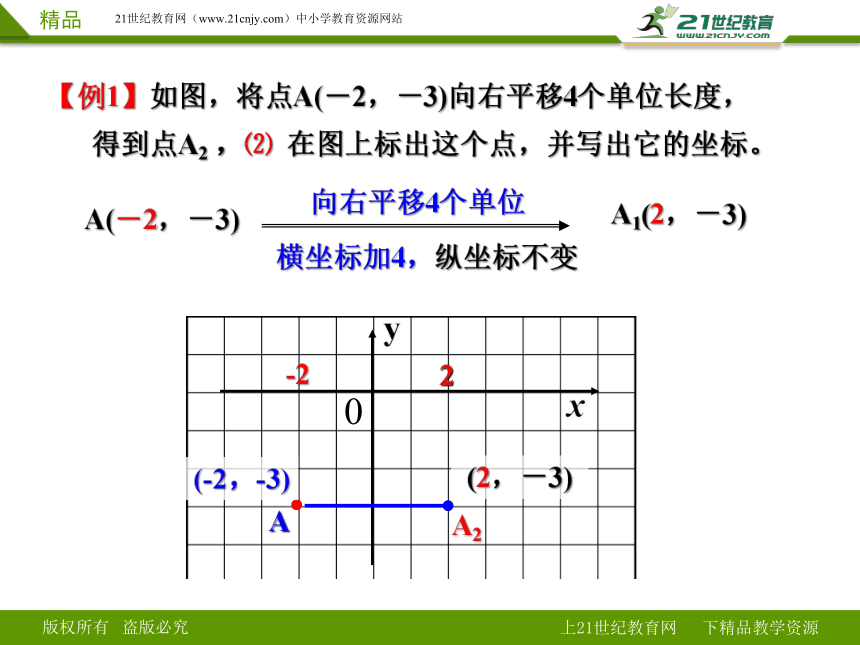
【例1】如图,将点A(-2,-3)向右平移4个单位长度,
得到点A2 ,⑵ 在图上标出这个点,并写出它的坐标。
●
(-2,-3)
A
x
y
0
A2
A(-2,-3)
A1(2,-3)
向右平移4个单位
(2,-3)
横坐标加4,纵坐标不变
-2
2
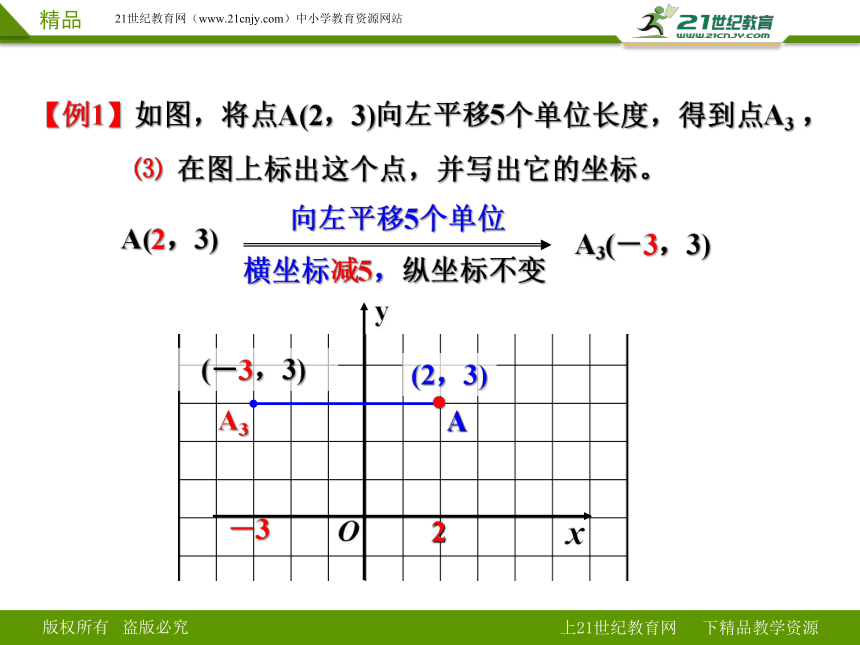
【例1】如图,将点A(2,3)向左平移5个单位长度,得到点A3 ,
⑶ 在图上标出这个点,并写出它的坐标。
(2,3)
A
x
y
O
A3
A(2,3)
A3(-3,3)
向左平移5个单位
(-3,3)
横坐标减5,纵坐标不变
●
2
-3
⑴在平面直角坐标系中,将点(x,y)向右或(向左)平移a个单位长度,可以得到对应点( ) 或( )
左右平移 引起坐标的变化规律
x-a,y
x+a,y
A(x,y)
A1(x+a,y)
向右平移a个单位
向左平移a个单位
A2(x-a,y)
横坐标加或减a,纵坐标不变.
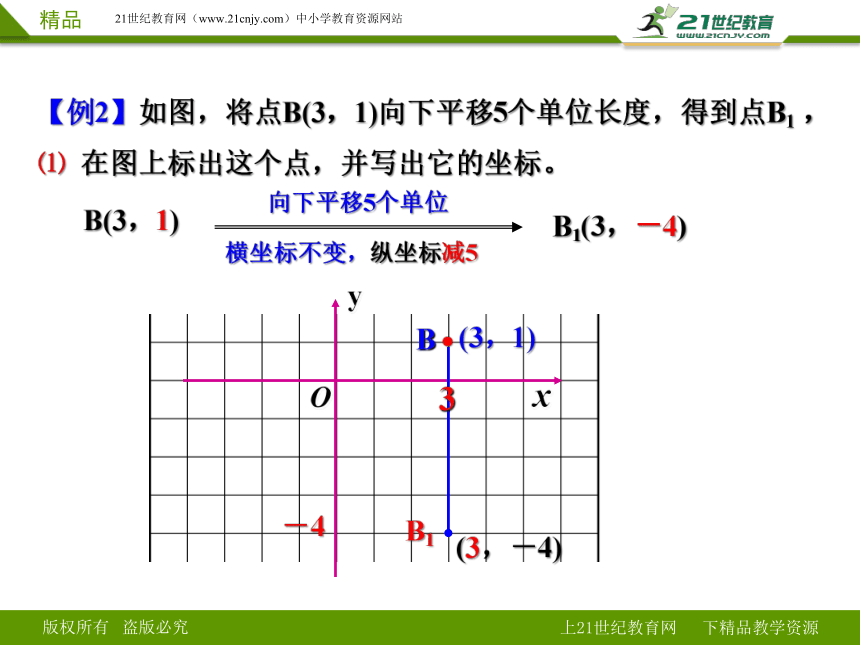
【例2】如图,将点B(3,1)向下平移5个单位长度,得到点B1 ,⑴ 在图上标出这个点,并写出它的坐标。
(3,1)
B
x
y
O
B1
B(3,1)
B1(3,-4)
向下平移5个单位
(3,-4)
横坐标不变,纵坐标减5
3
-4
●
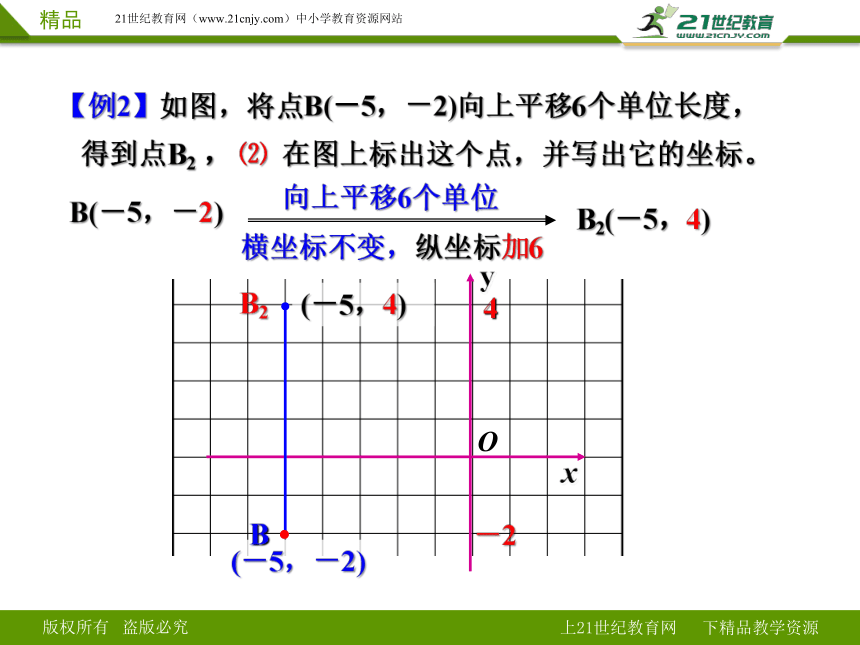
【例2】如图,将点B(-5,-2)向上平移6个单位长度,
得到点B2 , ⑵ 在图上标出这个点,并写出它的坐标。
(-5,-2)
B
x
y
O
B2
B(-5,-2)
B2(-5,4)
向上平移6个单位
(-5,4)
横坐标不变,纵坐标加6
-2
4
●
⑵在平面直角坐标系中,将点(x,y)向上或(向下)平移a个单位长度,可以得到对应点( ) 或( )
上下平移引起坐标的变化规律
x,y-a
x,y+a
A(x,y)
A1(x,y+a)
向上平移 a 个单位
向下平移 a 个单位
A2(x,y -a)
横坐标不变,纵坐标加或减 a.
【例3】如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E、F、G、H,它们的坐标分别是什么?如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
x
A
B
C
D
y
x
A
B
C
D
H
E
F
G
y
【例3】 ·······,两次平移后四个顶点相应变为点E、F、G、H,它们的坐标分别是什么?如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
x
A
B
C
D
H
E
F
G
y
解:⑴ E(6,-3)
、F(6,-4)
、F(7,-4)
、G(7,-3)
⑵ 如果直接平移正方形ABCD,使点A移到点E,
它和我们前面得到的正方形位置相同。
x
A
B
C
D
H
E
F
G
y
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到。
⑴这个图形上所有点的坐标都要发生相应的变化;
对一个图形进行平移
⑵ 反过来,从图形上点的坐标的某种变化,我们也
可以看出对这个图形进行了怎样的平移。
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到。
【例4】如图,△ABC三个顶点的坐标分别是A(4,3),
B(3,1),C(1,2)。
⑴将△ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,依次连接A1,B1,C1各点,所得△A1B1C1与△ABC的大小、形状和位置有什么关系?
1
2
3
4
0
-1
-2
-3
-4
1
2
3
4
x
y
5
A
B
C
A(4,3)
横坐标减去6
A1(-2,3)
纵坐标不变
B(3,1)
横坐标减去6
B1(-3,1)
纵坐标不变
C(1,2)
横坐标减去6
C1(-5,2)
纵坐标不变
●
A1
●
●
B1
C1
⑵将△ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2,B2,C2,依次连接A2,B2,C2各点,所得△A2B2C2与△ABC的大小、形状和位置有什么关系?
1
2
3
4
0
-1
-2
-3
-4
1
2
3
x
-1
-2
-3
-4
y
5
A
B
C
A(4,3)
横坐标不变
A2(4,-2)
纵坐标减5
B(3,1)
横坐标不变
B2(3,-4)
纵坐标减5
C(1,2)
横坐标不变
C2(1,-3)
纵坐标减5
●
A2
●
●
B2
C2
1
2
3
4
0
-1
-2
-3
-4
1
2
3
4
x
-1
-2
-3
-4
y
5
A
B
C
A1
B1
C1
A2
B2
C2
答:⑴ 所得△A1B1C1与△ABC的大小、形状完全相同, △A1B1C1可以看作将△ABC向左平移6个单位长度得到的。
⑵ 所得△A2B2C2与△ABC的大小、形状完全相同, △A2B2C2可以看作将△ABC向下平移5个单位长度得到的。
⑴ 在平面直角坐标系中,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右或(向左)平移a个单位长度;
⑵ 如果把各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上或(向下)平移a个单位长度。
归纳与整理
【例5】如图,将□ABCD向左平移2单位长度,然后再向上平移3个单位长度,可以得到□A/B/C/D/ ,画出平移后的图形,并指出其各个顶点的坐标。
1
2
3
4
0
-1
-2
-3
-4
1
2
3
4
x
-1
-2
-3
-4
y
5
A
B
C
D
A/
B/
C/
D/
A(-1,-2)
横坐标减2
A/(-3,1)
纵坐标加3
B(3,-2)
横坐标减2
B/(1,1)
纵坐标加3
C(4,1)
横坐标减2
C/(2,4)
纵坐标加3
D(0,1)
横坐标减2
D/(-2,4)
纵坐标加3
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
7.2.2用坐标表示
平移
人教版 七年级下
在平面直角坐标系中,对一个图形进行平移,图形上的点的位置发生了变化,坐标也一定会发生变化。
但是,平移过程中,坐标的变化规律是怎样呢?下面我们就通过具体例题来进行探究,从中发现其中的规律。
【例1】如图,将点A(-2,-3)向右平移5个单位长度,
得到点A1 ,⑴ 在图上标出这个点,并写出它的坐标。
●
(-2,-3)
A
x
y
0
A1
A(-2,-3)
A1(3,-3)
向右平移5个单位
(3,-3)
横坐标加5,纵坐标不变
-2
3
【例1】如图,将点A(-2,-3)向右平移4个单位长度,
得到点A2 ,⑵ 在图上标出这个点,并写出它的坐标。
●
(-2,-3)
A
x
y
0
A2
A(-2,-3)
A1(2,-3)
向右平移4个单位
(2,-3)
横坐标加4,纵坐标不变
-2
2
【例1】如图,将点A(2,3)向左平移5个单位长度,得到点A3 ,
⑶ 在图上标出这个点,并写出它的坐标。
(2,3)
A
x
y
O
A3
A(2,3)
A3(-3,3)
向左平移5个单位
(-3,3)
横坐标减5,纵坐标不变
●
2
-3
⑴在平面直角坐标系中,将点(x,y)向右或(向左)平移a个单位长度,可以得到对应点( ) 或( )
左右平移 引起坐标的变化规律
x-a,y
x+a,y
A(x,y)
A1(x+a,y)
向右平移a个单位
向左平移a个单位
A2(x-a,y)
横坐标加或减a,纵坐标不变.
【例2】如图,将点B(3,1)向下平移5个单位长度,得到点B1 ,⑴ 在图上标出这个点,并写出它的坐标。
(3,1)
B
x
y
O
B1
B(3,1)
B1(3,-4)
向下平移5个单位
(3,-4)
横坐标不变,纵坐标减5
3
-4
●
【例2】如图,将点B(-5,-2)向上平移6个单位长度,
得到点B2 , ⑵ 在图上标出这个点,并写出它的坐标。
(-5,-2)
B
x
y
O
B2
B(-5,-2)
B2(-5,4)
向上平移6个单位
(-5,4)
横坐标不变,纵坐标加6
-2
4
●
⑵在平面直角坐标系中,将点(x,y)向上或(向下)平移a个单位长度,可以得到对应点( ) 或( )
上下平移引起坐标的变化规律
x,y-a
x,y+a
A(x,y)
A1(x,y+a)
向上平移 a 个单位
向下平移 a 个单位
A2(x,y -a)
横坐标不变,纵坐标加或减 a.
【例3】如图,正方形ABCD四个顶点的坐标分别是A(-2,4),B(-2,3),C(-1,3),D(-1,4),将正方形ABCD向下平移7个单位长度,再向右平移8个单位长度,两次平移后四个顶点相应变为点E、F、G、H,它们的坐标分别是什么?如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
x
A
B
C
D
y
x
A
B
C
D
H
E
F
G
y
【例3】 ·······,两次平移后四个顶点相应变为点E、F、G、H,它们的坐标分别是什么?如果直接平移正方形ABCD,使点A移到点E,它和我们前面得到的正方形位置相同吗?
x
A
B
C
D
H
E
F
G
y
解:⑴ E(6,-3)
、F(6,-4)
、F(7,-4)
、G(7,-3)
⑵ 如果直接平移正方形ABCD,使点A移到点E,
它和我们前面得到的正方形位置相同。
x
A
B
C
D
H
E
F
G
y
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到。
⑴这个图形上所有点的坐标都要发生相应的变化;
对一个图形进行平移
⑵ 反过来,从图形上点的坐标的某种变化,我们也
可以看出对这个图形进行了怎样的平移。
一般地,将一个图形依次沿两个坐标轴方向平移所得到的图形,可以通过将原来的图形作一次平移得到。
【例4】如图,△ABC三个顶点的坐标分别是A(4,3),
B(3,1),C(1,2)。
⑴将△ABC三个顶点的横坐标都减去6,纵坐标不变,分别得到点A1,B1,C1,依次连接A1,B1,C1各点,所得△A1B1C1与△ABC的大小、形状和位置有什么关系?
1
2
3
4
0
-1
-2
-3
-4
1
2
3
4
x
y
5
A
B
C
A(4,3)
横坐标减去6
A1(-2,3)
纵坐标不变
B(3,1)
横坐标减去6
B1(-3,1)
纵坐标不变
C(1,2)
横坐标减去6
C1(-5,2)
纵坐标不变
●
A1
●
●
B1
C1
⑵将△ABC三个顶点的纵坐标都减去5,横坐标不变,分别得到点A2,B2,C2,依次连接A2,B2,C2各点,所得△A2B2C2与△ABC的大小、形状和位置有什么关系?
1
2
3
4
0
-1
-2
-3
-4
1
2
3
x
-1
-2
-3
-4
y
5
A
B
C
A(4,3)
横坐标不变
A2(4,-2)
纵坐标减5
B(3,1)
横坐标不变
B2(3,-4)
纵坐标减5
C(1,2)
横坐标不变
C2(1,-3)
纵坐标减5
●
A2
●
●
B2
C2
1
2
3
4
0
-1
-2
-3
-4
1
2
3
4
x
-1
-2
-3
-4
y
5
A
B
C
A1
B1
C1
A2
B2
C2
答:⑴ 所得△A1B1C1与△ABC的大小、形状完全相同, △A1B1C1可以看作将△ABC向左平移6个单位长度得到的。
⑵ 所得△A2B2C2与△ABC的大小、形状完全相同, △A2B2C2可以看作将△ABC向下平移5个单位长度得到的。
⑴ 在平面直角坐标系中,如果把一个图形各个点的横坐标都加(或减去)一个正数a,相应的新图形就是把原图形向右或(向左)平移a个单位长度;
⑵ 如果把各个点的纵坐标都加(或减去)一个正数a,相应的新图形就是把原图形向上或(向下)平移a个单位长度。
归纳与整理
【例5】如图,将□ABCD向左平移2单位长度,然后再向上平移3个单位长度,可以得到□A/B/C/D/ ,画出平移后的图形,并指出其各个顶点的坐标。
1
2
3
4
0
-1
-2
-3
-4
1
2
3
4
x
-1
-2
-3
-4
y
5
A
B
C
D
A/
B/
C/
D/
A(-1,-2)
横坐标减2
A/(-3,1)
纵坐标加3
B(3,-2)
横坐标减2
B/(1,1)
纵坐标加3
C(4,1)
横坐标减2
C/(2,4)
纵坐标加3
D(0,1)
横坐标减2
D/(-2,4)
纵坐标加3
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
