8.2用加减法解二元一次方程组(1)课件
图片预览







文档简介
(共23张PPT)
加减消元法⑴
人教版 七年级下
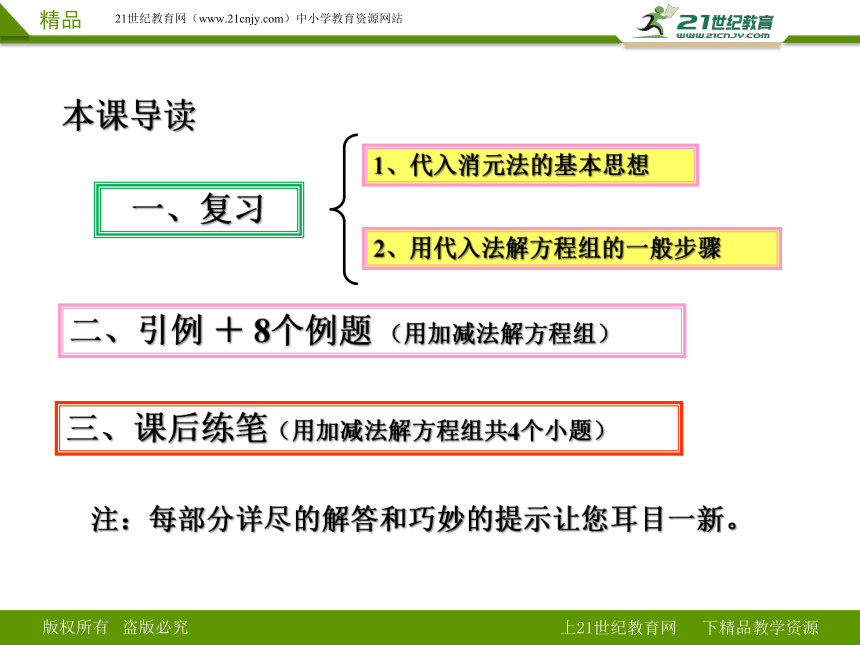
本课导读
一、复习
1、代入消元法的基本思想
2、用代入法解方程组的一般步骤
二、引例 + 8个例题 (用加减法解方程组)
三、课后练笔(用加减法解方程组共4个小题)
注:每部分详尽的解答和巧妙的提示让您耳目一新。
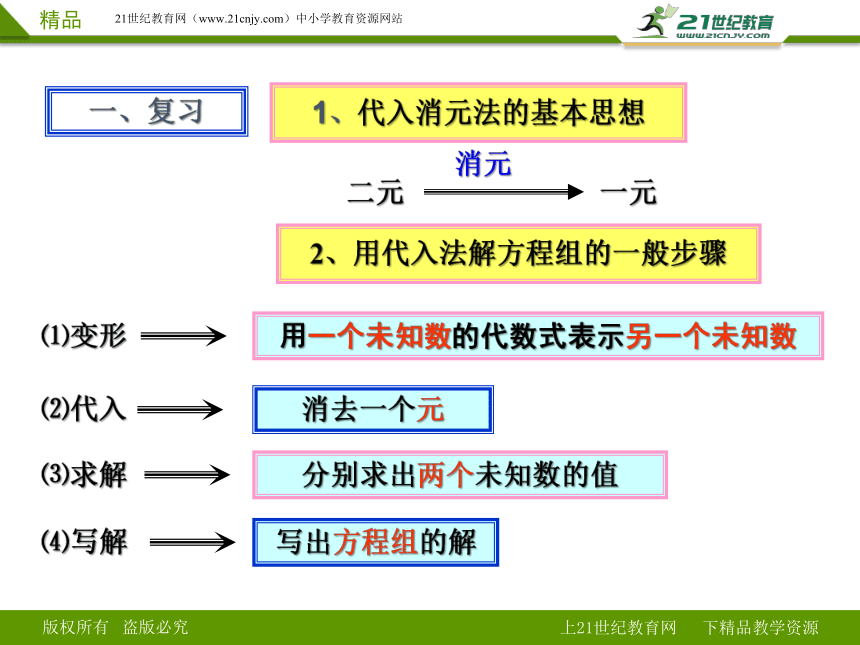
一、复习
1、代入消元法的基本思想
⑷写解
⑶求解
⑵代入
消去一个元
分别求出两个未知数的值
写出方程组的解
⑴变形
用一个未知数的代数式表示另一个未知数
2、用代入法解方程组的一般步骤
二元 一元
消元
用代入消元法解方程组.
二、巩固练习
①
②
解:由①,得
x =22-3y ③
把③代入②,得
2 (22-3y)+3y=26
y =6
把y=6代入③,得
x=4
所以原方程组的解是:
引例
请看下面解方程组的方法:
①
②
(2x+y)-(x+y)=8-6
解:方程 ②-①,得
2x+y-x-y=2
x=2
把x=2代入 ①,得
2+y=6
∴ y=4
所以原方程组的解是:
特征:y的系数相同
2、目的是消去其中的一个未知数y。
①
②
(2x+y)-(x+y)
=8-6
“方程 ②-①” 包含两层意思,就是:
1、方程 ②的左边减去方程①的左边;
同时方程②的右边减去方程①的右边。
【例1】解方程组
①
②
解:①+②,得
4x=8
x=2
把x=2代入 ①,得
2+2y=4
∴ y=1
∴ 原方程组的解是:
特征:y的系数
互为相反数
①
②
【例2】解方程组
解:①+②,得
19x=19
x=1
把x=1代入 ①,得
4+10y=11
y=0.7
所以原方程组的解是:
特征:y的系数互为相反数
两个二元一次方程中同一未知数的系数相反或相等时,直接把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。这种方法叫做加减消元法,简称加减法。
归纳
加减消元法
相反相加、相同相减
①
②
【例4】用加减法解二元一次方程组
你是否认为两个方程中的 x 和 y 的系数都没有相等或相反的,无法进行加或减?怎么办呢?
你是否觉得和前面三个例题不一样?
①
②
【例4】用加减法解二元一次方程组
利用等式的性质,将某个未知数的系数化为相等
因为,两个方程中y的系数是倍数有关系,
将y的系数化为相等比较方便,
10x+4y=50 ③
解:①×2,得
③-②,得
①
②
【例4】用加减法解二元一次方程组
7x=35
x=5
把x=5代入 ①,得
25+2y=25
y=0
所以原方程组的解是:
⑴ 当两个二元一次方程中同一个未知数的系数相反或相等
时,可以直接相加或相减。
心有灵犀一点通
⑵ 当两个二元一次方程中同一个未知数的系数是整倍数关系
时,可以将其中一个变形,化为系数相反或相等。
①
②
解:①×2,得
4x+6y=8 ③
③-②,得
15y=-30
y=-2
把y=-2代入①,得
2x-6=4
x=5
所以原方程组的解是:
解法一:消 x
【例5】解方程组
解:①×3,得
6x+9y=12 ③
③+②,得
10x=50
x=5
把x=5代入①,得
10+3y=4
y=-2
所以原方程组的解是:
①
②
解法二:消 y
【例5】解方程组
①
②
【例6】用加减法解二元一次方程组
解:①×2,得
18x+4y=30 ③
③-②,得
15x=20
把 x= 代入②,得
4+4y=10
所以原方程组的解是:
解法一:消 y
解:②×3,得
9x+12y=30 ③
③-①,得
10y=15
3x+6=10
所以原方程组的解是:
把y= 代入②,得
①
②
【例6】用加减法解二元一次方程组
解法二:消 x
⑶ 当两个未知数的系数都是整倍数关系时,就有两种解法,可以任意选择一个方程,化为系数相反或相等,再用加减法进行解题。
体会与感悟
【例7】用加减法解方程组
解:①×3,得
9x+12y=48 ③
② ×2,得
10x-12y=66 ④
③+④,得
19x=114
x=6
把x=6代入①,得
18+4y=16
y=-0.5
所以原方程组的解是:
①
②
【例8】用加减法解方程组
解:①×3,得
6x+15y=21 ③
② ×2,得
6x+4y=10 ④
③-④,得
11y=11
y=1
把y=1代入①,得
2x+5=7
x=1
所以原方程组的解是:
⑷ 当两个未知数的系数都不是整倍数关系时,就需要选择一个未知数,找到两个方程中的同一个未知数的这两个系数,将它们化为最小公倍数,就具备系数相反或相等,再用加减法进行解题。
方法与技巧
统一x的系数
统一y的系数
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
加减消元法⑴
人教版 七年级下
本课导读
一、复习
1、代入消元法的基本思想
2、用代入法解方程组的一般步骤
二、引例 + 8个例题 (用加减法解方程组)
三、课后练笔(用加减法解方程组共4个小题)
注:每部分详尽的解答和巧妙的提示让您耳目一新。
一、复习
1、代入消元法的基本思想
⑷写解
⑶求解
⑵代入
消去一个元
分别求出两个未知数的值
写出方程组的解
⑴变形
用一个未知数的代数式表示另一个未知数
2、用代入法解方程组的一般步骤
二元 一元
消元
用代入消元法解方程组.
二、巩固练习
①
②
解:由①,得
x =22-3y ③
把③代入②,得
2 (22-3y)+3y=26
y =6
把y=6代入③,得
x=4
所以原方程组的解是:
引例
请看下面解方程组的方法:
①
②
(2x+y)-(x+y)=8-6
解:方程 ②-①,得
2x+y-x-y=2
x=2
把x=2代入 ①,得
2+y=6
∴ y=4
所以原方程组的解是:
特征:y的系数相同
2、目的是消去其中的一个未知数y。
①
②
(2x+y)-(x+y)
=8-6
“方程 ②-①” 包含两层意思,就是:
1、方程 ②的左边减去方程①的左边;
同时方程②的右边减去方程①的右边。
【例1】解方程组
①
②
解:①+②,得
4x=8
x=2
把x=2代入 ①,得
2+2y=4
∴ y=1
∴ 原方程组的解是:
特征:y的系数
互为相反数
①
②
【例2】解方程组
解:①+②,得
19x=19
x=1
把x=1代入 ①,得
4+10y=11
y=0.7
所以原方程组的解是:
特征:y的系数互为相反数
两个二元一次方程中同一未知数的系数相反或相等时,直接把这两个方程的两边分别相加或相减,就能消去这个未知数,得到一个一元一次方程。这种方法叫做加减消元法,简称加减法。
归纳
加减消元法
相反相加、相同相减
①
②
【例4】用加减法解二元一次方程组
你是否认为两个方程中的 x 和 y 的系数都没有相等或相反的,无法进行加或减?怎么办呢?
你是否觉得和前面三个例题不一样?
①
②
【例4】用加减法解二元一次方程组
利用等式的性质,将某个未知数的系数化为相等
因为,两个方程中y的系数是倍数有关系,
将y的系数化为相等比较方便,
10x+4y=50 ③
解:①×2,得
③-②,得
①
②
【例4】用加减法解二元一次方程组
7x=35
x=5
把x=5代入 ①,得
25+2y=25
y=0
所以原方程组的解是:
⑴ 当两个二元一次方程中同一个未知数的系数相反或相等
时,可以直接相加或相减。
心有灵犀一点通
⑵ 当两个二元一次方程中同一个未知数的系数是整倍数关系
时,可以将其中一个变形,化为系数相反或相等。
①
②
解:①×2,得
4x+6y=8 ③
③-②,得
15y=-30
y=-2
把y=-2代入①,得
2x-6=4
x=5
所以原方程组的解是:
解法一:消 x
【例5】解方程组
解:①×3,得
6x+9y=12 ③
③+②,得
10x=50
x=5
把x=5代入①,得
10+3y=4
y=-2
所以原方程组的解是:
①
②
解法二:消 y
【例5】解方程组
①
②
【例6】用加减法解二元一次方程组
解:①×2,得
18x+4y=30 ③
③-②,得
15x=20
把 x= 代入②,得
4+4y=10
所以原方程组的解是:
解法一:消 y
解:②×3,得
9x+12y=30 ③
③-①,得
10y=15
3x+6=10
所以原方程组的解是:
把y= 代入②,得
①
②
【例6】用加减法解二元一次方程组
解法二:消 x
⑶ 当两个未知数的系数都是整倍数关系时,就有两种解法,可以任意选择一个方程,化为系数相反或相等,再用加减法进行解题。
体会与感悟
【例7】用加减法解方程组
解:①×3,得
9x+12y=48 ③
② ×2,得
10x-12y=66 ④
③+④,得
19x=114
x=6
把x=6代入①,得
18+4y=16
y=-0.5
所以原方程组的解是:
①
②
【例8】用加减法解方程组
解:①×3,得
6x+15y=21 ③
② ×2,得
6x+4y=10 ④
③-④,得
11y=11
y=1
把y=1代入①,得
2x+5=7
x=1
所以原方程组的解是:
⑷ 当两个未知数的系数都不是整倍数关系时,就需要选择一个未知数,找到两个方程中的同一个未知数的这两个系数,将它们化为最小公倍数,就具备系数相反或相等,再用加减法进行解题。
方法与技巧
统一x的系数
统一y的系数
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
