9.1.2利用不等式的性质解不等式(课件)
文档属性
| 名称 | 9.1.2利用不等式的性质解不等式(课件) |

|
|
| 格式 | ppt | ||
| 文件大小 | 3.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-08 00:00:00 | ||
图片预览




文档简介
(共12张PPT)
利用不等式的性质
解不等式
人教版 七年级下
空心圆圈
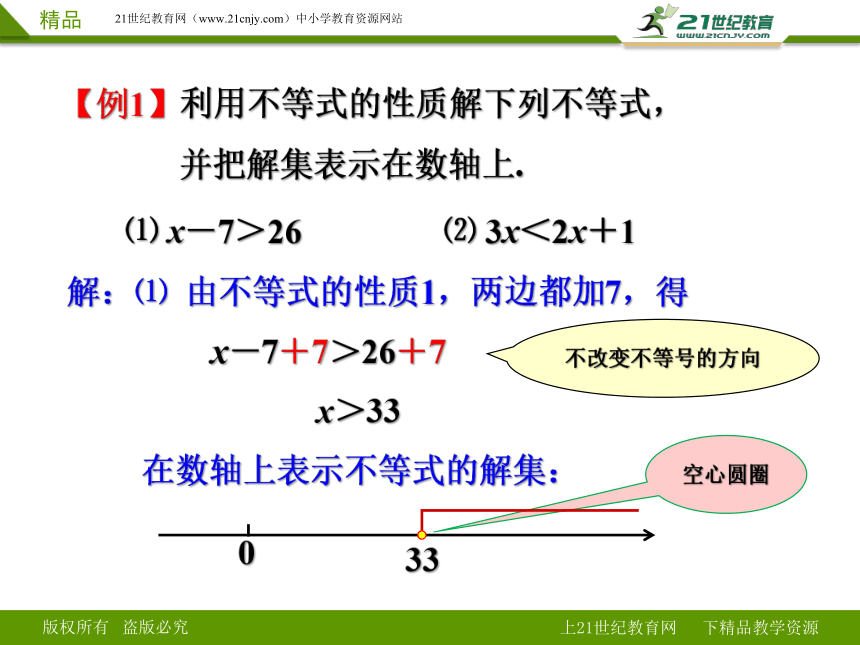
【例1】利用不等式的性质解下列不等式,
并把解集表示在数轴上.
⑴ x-7>26 ⑵ 3x<2x+1
解:⑴ 由不等式的性质1,两边都加7,得
x-7+7>26+7
x>33
在数轴上表示不等式的解集:
0
33
不改变不等号的方向
【例1】利用不等式的性质解下列不等式,
并把解集表示在数轴上.
⑴ x-7>26 ⑵ 3x<2x+1
解:⑵ 由不等式的性质1,两边都减2x,得
3x-2x<2x+1-2x
x<1
在数轴上表示不等式的解集:
0
1
空心圆圈
不改变不等号的方向
空心圆圈
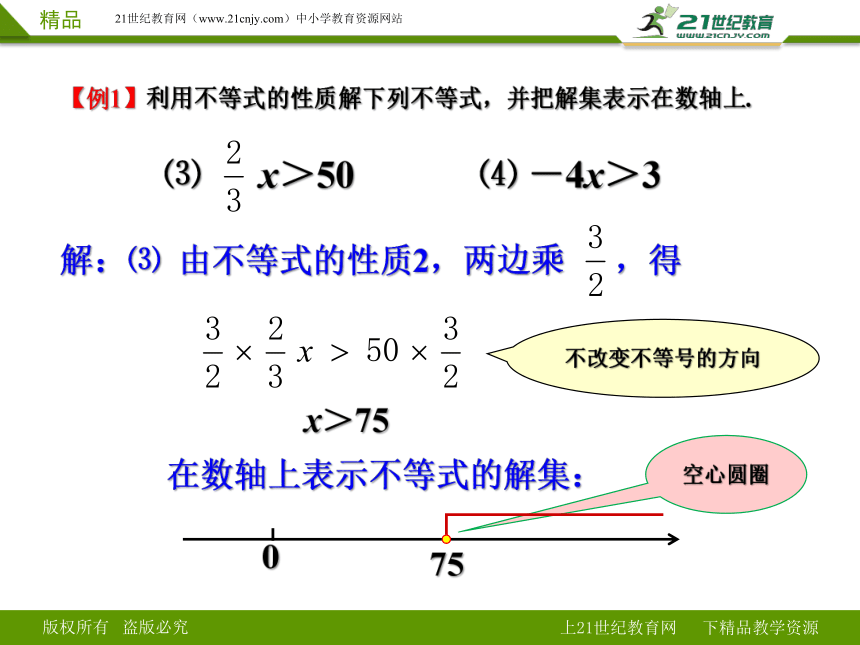
⑶ x>50 ⑷ -4x>3
【例1】利用不等式的性质解下列不等式,并把解集表示在数轴上.
解:⑶ 由不等式的性质2,两边乘 ,得
x>75
在数轴上表示不等式的解集:
0
75
不改变不等号的方向
⑶ x>50 ⑷ -4x>3
【例1】利用不等式的性质解下列不等式,并把解集表示在数轴上.
解:⑷ 由不等式的性质3,两边除以-4,得
在数轴上表示不等式的解集:
0
改变不等号的方向
空心圆圈
像a≥b或a≤b这样的式子,也经常用来表示两个数量的大小关系。
例如:为了表示2017年1月20日安阳的最低气温是-7℃,最高气温是5℃,我们可以用t表示这一天任一时刻的气温,t是随时间变化的,但是它有一定的变化范围,即
t≥-7℃且t≤5℃
或者表示为 -7℃≤t≤5℃
符号“≥”读作:大于或等于,
t≥-7℃且t≤5℃
或者表示为 -7℃≤t≤5℃
而a≥b 或a≤b形式的式子,同样具有前面所说的不等式的三个基本性质。
或读作:不小于.
符号“≤”读作:小于或等于,
或读作:不大于.
即解不等式时,也是运用不等式的三个基本性质。
【例2】某长方体形状的容器长5cm,宽3cm,高10cm. 容器内原有水的高度为3cm,现准备向它继续注水。用V(单位:cm3)表示新注水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积
的和不能超过容器的容积,即
5cm
3cm
10cm
3cm
V+5×3×3≤5×3×10
V=?
5×3×3
5×3×10
V≤105
V+45≤150
又由于新注入水的体积V不能是负数,
解:新注入水的体积V与原有水的体积
的和不能超过容器的容积,即
5cm
3cm
10cm
3cm
V+5×3×3≤5×3×10
V=?
5×3×3
5×3×10
V≤105
V+45≤150
又由于新注入水的体积V不能是负数,
V的取值范围是:
V≥0且V≤105
即 0≤V≤105 (读作:V大于等于0,小于等于105)
在数轴上表示V的范围是:
0
105
实心圆点
小结
1、会利用不等式的三个性质解不等式;
2、特别要注意:
⑴ 用不等式的性质1和性质2都不改变不等号的方向,
⑵ 用不等式的性质3时,一定要改变不等号的方向!
3、在数轴上表示解集时要注意:
⑴“>、<”都用空心圆圈!⑵“≥、≤”都用实心圆点!
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
利用不等式的性质
解不等式
人教版 七年级下
空心圆圈
【例1】利用不等式的性质解下列不等式,
并把解集表示在数轴上.
⑴ x-7>26 ⑵ 3x<2x+1
解:⑴ 由不等式的性质1,两边都加7,得
x-7+7>26+7
x>33
在数轴上表示不等式的解集:
0
33
不改变不等号的方向
【例1】利用不等式的性质解下列不等式,
并把解集表示在数轴上.
⑴ x-7>26 ⑵ 3x<2x+1
解:⑵ 由不等式的性质1,两边都减2x,得
3x-2x<2x+1-2x
x<1
在数轴上表示不等式的解集:
0
1
空心圆圈
不改变不等号的方向
空心圆圈
⑶ x>50 ⑷ -4x>3
【例1】利用不等式的性质解下列不等式,并把解集表示在数轴上.
解:⑶ 由不等式的性质2,两边乘 ,得
x>75
在数轴上表示不等式的解集:
0
75
不改变不等号的方向
⑶ x>50 ⑷ -4x>3
【例1】利用不等式的性质解下列不等式,并把解集表示在数轴上.
解:⑷ 由不等式的性质3,两边除以-4,得
在数轴上表示不等式的解集:
0
改变不等号的方向
空心圆圈
像a≥b或a≤b这样的式子,也经常用来表示两个数量的大小关系。
例如:为了表示2017年1月20日安阳的最低气温是-7℃,最高气温是5℃,我们可以用t表示这一天任一时刻的气温,t是随时间变化的,但是它有一定的变化范围,即
t≥-7℃且t≤5℃
或者表示为 -7℃≤t≤5℃
符号“≥”读作:大于或等于,
t≥-7℃且t≤5℃
或者表示为 -7℃≤t≤5℃
而a≥b 或a≤b形式的式子,同样具有前面所说的不等式的三个基本性质。
或读作:不小于.
符号“≤”读作:小于或等于,
或读作:不大于.
即解不等式时,也是运用不等式的三个基本性质。
【例2】某长方体形状的容器长5cm,宽3cm,高10cm. 容器内原有水的高度为3cm,现准备向它继续注水。用V(单位:cm3)表示新注水的体积,写出V的取值范围。
解:新注入水的体积V与原有水的体积
的和不能超过容器的容积,即
5cm
3cm
10cm
3cm
V+5×3×3≤5×3×10
V=?
5×3×3
5×3×10
V≤105
V+45≤150
又由于新注入水的体积V不能是负数,
解:新注入水的体积V与原有水的体积
的和不能超过容器的容积,即
5cm
3cm
10cm
3cm
V+5×3×3≤5×3×10
V=?
5×3×3
5×3×10
V≤105
V+45≤150
又由于新注入水的体积V不能是负数,
V的取值范围是:
V≥0且V≤105
即 0≤V≤105 (读作:V大于等于0,小于等于105)
在数轴上表示V的范围是:
0
105
实心圆点
小结
1、会利用不等式的三个性质解不等式;
2、特别要注意:
⑴ 用不等式的性质1和性质2都不改变不等号的方向,
⑵ 用不等式的性质3时,一定要改变不等号的方向!
3、在数轴上表示解集时要注意:
⑴“>、<”都用空心圆圈!⑵“≥、≤”都用实心圆点!
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
