9.3.2 一元一次不等式组的应用(2)课件
文档属性
| 名称 | 9.3.2 一元一次不等式组的应用(2)课件 |  | |
| 格式 | ppt | ||
| 文件大小 | 2.4MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-10 10:43:58 | ||
图片预览








文档简介
(共23张PPT)
一元一次不等式组的应用(2)
人教版 七年级下
1、将若干只鸡放在若干个笼里,若每个笼里放4只鸡,则剩下一只鸡无笼可放;若每个笼里放5只鸡,则有一笼无鸡可放。那么有几只鸡?多少个笼?
分析:设有笼 x 个,有鸡 y 只;则
由 “若每个笼里放4只,则剩下一只鸡无笼可放;”
y=4x+1
由 “若每个笼里放5只鸡,则有一笼无鸡可放”
5 (x-1)
y-
=0
把 ① 代入 ②,得
①
②
4x+1-5 (x-1) =0
x =6
解:设有笼 x 个,有鸡 y 只,则
1、将若干只鸡放在若干个笼里,若每个笼里放4只鸡,则剩下一只鸡无笼可放;若每个笼里放5只鸡,则有一笼无鸡可放。那么有几只鸡?多少个笼?
y=4×6+1
=25
答:有25只鸡,6个笼。
把 x =6 代入① ,得
∴方程组的解为:
x=6
y=25
2、一群女生住若干间宿舍,每间住4人,剩19人无房住;每间住6人,有一间宿舍住不满。⑴设有x 间宿舍,请写出x应满足的不等式组。⑵可能有多少间宿舍和多少名学生?
解:⑴ 设有x间宿舍,则有(4x+19)名女生,根据题意,得
⑵ 解不等式组,得
9.5<x≤12
因为 x 是整数,所以 x=10,11,12
因此有三种可能,
第一种:有10间宿舍,59名女生;
第二种:有11间宿舍,63名女生;
第三种:有12间宿舍,67名女生。
3、一堆玩具分给若干个小朋友,若每人分2件,则剩余3件;若前面每人分3件,则最后一个人得到的玩具数不足2件。求小朋友的人数与玩具数。
解:设小朋友有 x 人,则玩具有2x+3件;
①
②
解不等式 ①,得
x≤5
x > 4
解不等式 ②,得
不等式组的解集是
4<x≤5
x是整数,只能取 x=5
2x+3
=13(个)
答:有5个小朋友,
13个玩具。
4、把若干个橘子分给几个小朋友,若每个小朋友分3个则多余8个;每个小朋友分5个则最后一名小朋友分到了橘子但不满5个。问一共有多少名小朋友?多少个橘子?
解:设有 x 名小朋友,则有橘子3x+8个;
①
②
解不等式 ①,得
x≤6
x > 4
解不等式 ②,得
不等式组的解集是
4<x≤6
x是整数,可取 x=5或6
3x+8
=23 (个)
答:有5个小朋友,23个橘子或有6个小朋友,26个橘子。
3x+8
=26 (个)
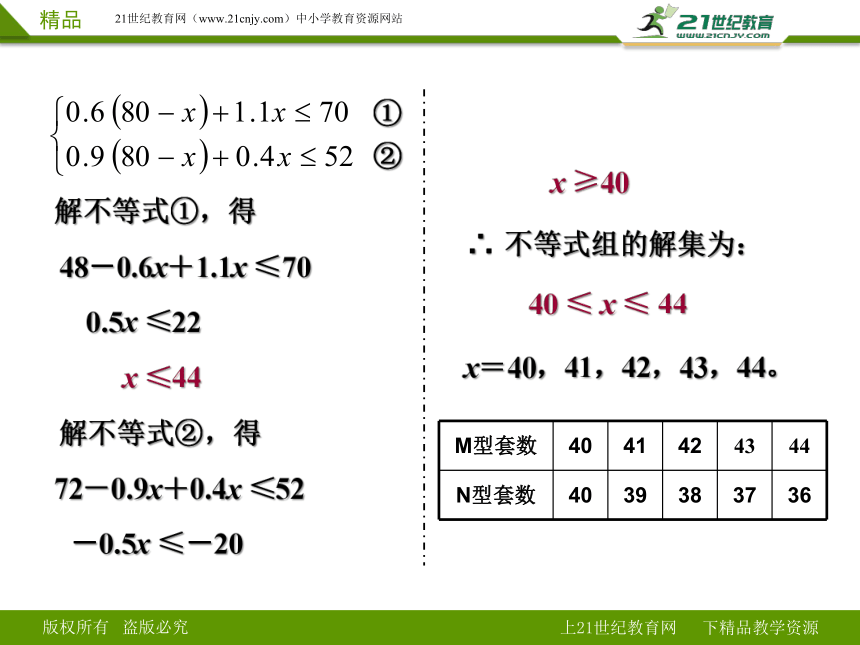
5、已知利民服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M,N两种型号的时装共80套,已知做一套M型号时装需A种布料0.6米,B种布料0.9米;做一套N型号时装需A种布料1.1米,B种布料0.4米;若设生产N型号的时装套数为x,用这批布料生产这两种型号的时装有几种方案。
分析:M型用A米数+N型用A米数≤70米
解:根据题意,得
M型用B米数+N型用B米数≤52米
①
②
①
②
解不等式①,得
48-0.6x+1.1x ≤70
0.5x ≤22
x ≤44
解不等式②,得
72-0.9x+0.4x ≤52
-0.5x ≤-20
x ≥40
∴ 不等式组的解集为:
40 ≤ x ≤ 44
x=40,41,42,43,44。
M型套数 40 41 42 43 44
N型套数 40 39 38 37 36
6、火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用A、B两种型号的车厢共50节,将这批货物运至北京,已知每节A型货厢的运费是0.5万元,每节B型货厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,共有哪几种方案?请你设计出来;并说明哪种方案的运费最少?
6、火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用A、B两种型号的车厢共50节,将这批货物运至北京,已知每节A型货厢的运费是0.5万元,每节B型货厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,共有哪几种方案?请你设计出来;并说明哪种方案的运费最少?
A型装甲货吨数+B型装甲货吨数≥1530
解:设安排A型车厢x节, 则
A型装乙货吨数+B型装乙货吨数≥1150
①
②
解不等式①,得
35x+1250-25x ≥1530
①
②
解不等式①,得
35x+1250-25x ≥1530
10x ≥280
x≥28
解不等式②,得
15x+1750-35x ≥1150
-20x ≥-600
x ≤30
∴ 不等式组的解集为:
28≤x≤30
x=28,29,30。
A型车厢节数 28 29 30
B型车厢节数 22 21 20
0.5×28+0.8×22
=31.6 (万元)
0.5×29+0.8×21
=31.3 (万元)
0.5×30+0.8×20
=31.0 (万元)
7、某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A、B两种产品共50件。已知生产一件A种产品需甲种原料9kg,乙种原料3kg,生产一件B种产品需甲种原料4kg,乙种原料10kg。
⑴、设生产x件A种产品,写出x应满足的不等式组;
⑵、有哪几种符合题意的生产方案?
分析:A用甲kg数+ B用甲kg数≤360kg
解:⑴ 根据题意,得
A用乙kg数+ B用乙kg数≤290kg
7、某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A、B两种产品共50件。已知生产一件A种产品需甲种原料9kg,乙种原料3kg,生产一件B种产品需甲种原料4kg,乙种原料10kg。
⑴、设生产x件A种产品,写出x应满足的不等式组;
⑵、有哪几种符合题意的生产方案?
解:⑴ 根据题意,得
①
②
30 ≤x≤32
⑵ 解不等式组,得
x=30,31,32。
生产A种件数 30 31 32
生产B种件数 20 19 18
8、某中学为了加强现代信息技术教学,要投资建一个初级计算机房和一个高级计算机房,每个机房配置教师用机一台,学生用机若干台,其中初级机房教师用机每台8000元,学生用机每台3500元;高级机房教师用机每台11500元,学生用机每台7000元,已知两机房购买计算机的总钱数相等,且学校用于购置计算机的投资不少于40万元,也不超过42万元,则此校建的初级机房、高级机房各有多少台计算机?
8、某中学为了加强现代信息技术教学,要投资建一个初级计算机房和一个高级计算机房,每个机房配置教师用机一台,学生用机若干台,其中初级机房教师用机每台8000元,学生用机每台3500元;高级机房教师用机每台11500元,学生用机每台7000元,已知两机房购买计算机的总钱数相等,且学校用于购置计算机的投资不少于40万元,也不超过42万元,则此校建的初级机房、高级机房各有多少台计算机?
解:设初级机房学生用机 x 台,高级机房学生用机 y 台;
①
②
解不等式②,得
解:设初级机房学生用机 x 台,高级机房学生用机 y 台;则
①
②
解不等式②,得
整数 x=55, 56, 57。
y=27,27.5, 28。
答:初级机房学生用机55台,高级机房学生用机27台;
或初级机房学生用机57台,高级机房学生用机28台.
9、某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
A B
成本(万元 / 套) 25 28
售价(万元 / 套) 30 34
⑴ 该公司对这两种户型住房有哪几种建房方案?
解:设A种户型住房建 x 套,则B种户型住房建 (80- x)套,
48≤x≤50
解,得
⑴ 该公司对这两种户型住房有哪几种建房方案?
解:设A种户型住房建 x 套,则B种户型住房建 (80- x)套,
48≤x≤50
解,得
x=48,49,50。
A型套数 48 49 50
B型套数 32 31 30
A B
成本(万元 / 套) 25 28
售价(万元 / 套) 30 34
⑵ 该公司如何建房获得利润最大?
A型套数 48 49 50
B型套数 32 31 30
解:设该公司建房获得利润为W万元,
W=5x+6×(80-x)
=480-x
当x=48时,利润最大,
W最大=480-48=432 (万元)
A B
成本(万元 / 套) 25 28
售价(万元 / 套) 30 34
⑶ 根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得的利润最大?
⑶由题意,知
W=(5+a) x+6×(80-x)
=480+(a-1) x
① 当a-1<0时,即0<a<1时,且x=48,利润W最大,
即A型住房建48套, B型住房建32套,利润最大,
② 当a-1=0时,即a=1时,三种建房方案获得利润相等。
③ 当a-1>0时,即a>1时,且 x=50,利润W最大。
即A型住房建50套, B型住房建30套,利润最大,
⑶ 根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得的利润最大?
① 当a-1<0时,即0<a<1时,且x=48,利润W最大,
即A型住房建48套, B型住房建32套,利润最大,
⑶由题意,知
W=(5+a) x+6×(80-x)
=480+(a-1) x
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
一元一次不等式组的应用(2)
人教版 七年级下
1、将若干只鸡放在若干个笼里,若每个笼里放4只鸡,则剩下一只鸡无笼可放;若每个笼里放5只鸡,则有一笼无鸡可放。那么有几只鸡?多少个笼?
分析:设有笼 x 个,有鸡 y 只;则
由 “若每个笼里放4只,则剩下一只鸡无笼可放;”
y=4x+1
由 “若每个笼里放5只鸡,则有一笼无鸡可放”
5 (x-1)
y-
=0
把 ① 代入 ②,得
①
②
4x+1-5 (x-1) =0
x =6
解:设有笼 x 个,有鸡 y 只,则
1、将若干只鸡放在若干个笼里,若每个笼里放4只鸡,则剩下一只鸡无笼可放;若每个笼里放5只鸡,则有一笼无鸡可放。那么有几只鸡?多少个笼?
y=4×6+1
=25
答:有25只鸡,6个笼。
把 x =6 代入① ,得
∴方程组的解为:
x=6
y=25
2、一群女生住若干间宿舍,每间住4人,剩19人无房住;每间住6人,有一间宿舍住不满。⑴设有x 间宿舍,请写出x应满足的不等式组。⑵可能有多少间宿舍和多少名学生?
解:⑴ 设有x间宿舍,则有(4x+19)名女生,根据题意,得
⑵ 解不等式组,得
9.5<x≤12
因为 x 是整数,所以 x=10,11,12
因此有三种可能,
第一种:有10间宿舍,59名女生;
第二种:有11间宿舍,63名女生;
第三种:有12间宿舍,67名女生。
3、一堆玩具分给若干个小朋友,若每人分2件,则剩余3件;若前面每人分3件,则最后一个人得到的玩具数不足2件。求小朋友的人数与玩具数。
解:设小朋友有 x 人,则玩具有2x+3件;
①
②
解不等式 ①,得
x≤5
x > 4
解不等式 ②,得
不等式组的解集是
4<x≤5
x是整数,只能取 x=5
2x+3
=13(个)
答:有5个小朋友,
13个玩具。
4、把若干个橘子分给几个小朋友,若每个小朋友分3个则多余8个;每个小朋友分5个则最后一名小朋友分到了橘子但不满5个。问一共有多少名小朋友?多少个橘子?
解:设有 x 名小朋友,则有橘子3x+8个;
①
②
解不等式 ①,得
x≤6
x > 4
解不等式 ②,得
不等式组的解集是
4<x≤6
x是整数,可取 x=5或6
3x+8
=23 (个)
答:有5个小朋友,23个橘子或有6个小朋友,26个橘子。
3x+8
=26 (个)
5、已知利民服装厂现有A种布料70米,B种布料52米,现计划用这两种布料生产M,N两种型号的时装共80套,已知做一套M型号时装需A种布料0.6米,B种布料0.9米;做一套N型号时装需A种布料1.1米,B种布料0.4米;若设生产N型号的时装套数为x,用这批布料生产这两种型号的时装有几种方案。
分析:M型用A米数+N型用A米数≤70米
解:根据题意,得
M型用B米数+N型用B米数≤52米
①
②
①
②
解不等式①,得
48-0.6x+1.1x ≤70
0.5x ≤22
x ≤44
解不等式②,得
72-0.9x+0.4x ≤52
-0.5x ≤-20
x ≥40
∴ 不等式组的解集为:
40 ≤ x ≤ 44
x=40,41,42,43,44。
M型套数 40 41 42 43 44
N型套数 40 39 38 37 36
6、火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用A、B两种型号的车厢共50节,将这批货物运至北京,已知每节A型货厢的运费是0.5万元,每节B型货厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,共有哪几种方案?请你设计出来;并说明哪种方案的运费最少?
6、火车站有某公司待运的甲种货物1530吨,乙种货物1150吨,现计划用A、B两种型号的车厢共50节,将这批货物运至北京,已知每节A型货厢的运费是0.5万元,每节B型货厢的运费是0.8万元;甲种货物35吨和乙种货物15吨可装满一节A型货厢,甲种货物25吨和乙种货物35吨可装满一节B型货厢,按此要求安排A、B两种货厢的节数,共有哪几种方案?请你设计出来;并说明哪种方案的运费最少?
A型装甲货吨数+B型装甲货吨数≥1530
解:设安排A型车厢x节, 则
A型装乙货吨数+B型装乙货吨数≥1150
①
②
解不等式①,得
35x+1250-25x ≥1530
①
②
解不等式①,得
35x+1250-25x ≥1530
10x ≥280
x≥28
解不等式②,得
15x+1750-35x ≥1150
-20x ≥-600
x ≤30
∴ 不等式组的解集为:
28≤x≤30
x=28,29,30。
A型车厢节数 28 29 30
B型车厢节数 22 21 20
0.5×28+0.8×22
=31.6 (万元)
0.5×29+0.8×21
=31.3 (万元)
0.5×30+0.8×20
=31.0 (万元)
7、某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A、B两种产品共50件。已知生产一件A种产品需甲种原料9kg,乙种原料3kg,生产一件B种产品需甲种原料4kg,乙种原料10kg。
⑴、设生产x件A种产品,写出x应满足的不等式组;
⑵、有哪几种符合题意的生产方案?
分析:A用甲kg数+ B用甲kg数≤360kg
解:⑴ 根据题意,得
A用乙kg数+ B用乙kg数≤290kg
7、某工厂现有甲种原料360kg,乙种原料290kg,计划利用这两种原料生产A、B两种产品共50件。已知生产一件A种产品需甲种原料9kg,乙种原料3kg,生产一件B种产品需甲种原料4kg,乙种原料10kg。
⑴、设生产x件A种产品,写出x应满足的不等式组;
⑵、有哪几种符合题意的生产方案?
解:⑴ 根据题意,得
①
②
30 ≤x≤32
⑵ 解不等式组,得
x=30,31,32。
生产A种件数 30 31 32
生产B种件数 20 19 18
8、某中学为了加强现代信息技术教学,要投资建一个初级计算机房和一个高级计算机房,每个机房配置教师用机一台,学生用机若干台,其中初级机房教师用机每台8000元,学生用机每台3500元;高级机房教师用机每台11500元,学生用机每台7000元,已知两机房购买计算机的总钱数相等,且学校用于购置计算机的投资不少于40万元,也不超过42万元,则此校建的初级机房、高级机房各有多少台计算机?
8、某中学为了加强现代信息技术教学,要投资建一个初级计算机房和一个高级计算机房,每个机房配置教师用机一台,学生用机若干台,其中初级机房教师用机每台8000元,学生用机每台3500元;高级机房教师用机每台11500元,学生用机每台7000元,已知两机房购买计算机的总钱数相等,且学校用于购置计算机的投资不少于40万元,也不超过42万元,则此校建的初级机房、高级机房各有多少台计算机?
解:设初级机房学生用机 x 台,高级机房学生用机 y 台;
①
②
解不等式②,得
解:设初级机房学生用机 x 台,高级机房学生用机 y 台;则
①
②
解不等式②,得
整数 x=55, 56, 57。
y=27,27.5, 28。
答:初级机房学生用机55台,高级机房学生用机27台;
或初级机房学生用机57台,高级机房学生用机28台.
9、某房地产开发公司计划建A、B两种户型的住房共80套,该公司所筹资金不少于2090万元,但不超过2096万元,且所筹资金全部用于建房,两种户型的建房成本和售价如下表:
A B
成本(万元 / 套) 25 28
售价(万元 / 套) 30 34
⑴ 该公司对这两种户型住房有哪几种建房方案?
解:设A种户型住房建 x 套,则B种户型住房建 (80- x)套,
48≤x≤50
解,得
⑴ 该公司对这两种户型住房有哪几种建房方案?
解:设A种户型住房建 x 套,则B种户型住房建 (80- x)套,
48≤x≤50
解,得
x=48,49,50。
A型套数 48 49 50
B型套数 32 31 30
A B
成本(万元 / 套) 25 28
售价(万元 / 套) 30 34
⑵ 该公司如何建房获得利润最大?
A型套数 48 49 50
B型套数 32 31 30
解:设该公司建房获得利润为W万元,
W=5x+6×(80-x)
=480-x
当x=48时,利润最大,
W最大=480-48=432 (万元)
A B
成本(万元 / 套) 25 28
售价(万元 / 套) 30 34
⑶ 根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得的利润最大?
⑶由题意,知
W=(5+a) x+6×(80-x)
=480+(a-1) x
① 当a-1<0时,即0<a<1时,且x=48,利润W最大,
即A型住房建48套, B型住房建32套,利润最大,
② 当a-1=0时,即a=1时,三种建房方案获得利润相等。
③ 当a-1>0时,即a>1时,且 x=50,利润W最大。
即A型住房建50套, B型住房建30套,利润最大,
⑶ 根据市场调查,每套B型住房的售价不会改变,每套A型住房的售价将会提高a万元(a>0),且所建的两种住房可全部售出,该公司又将如何建房获得的利润最大?
① 当a-1<0时,即0<a<1时,且x=48,利润W最大,
即A型住房建48套, B型住房建32套,利润最大,
⑶由题意,知
W=(5+a) x+6×(80-x)
=480+(a-1) x
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
