2.2 探索直线平行的条件(2)同步练习
文档属性
| 名称 | 2.2 探索直线平行的条件(2)同步练习 |  | |
| 格式 | docx | ||
| 文件大小 | 306.2KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-09 10:55:08 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
2.2探索直线平行的条件(2)同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
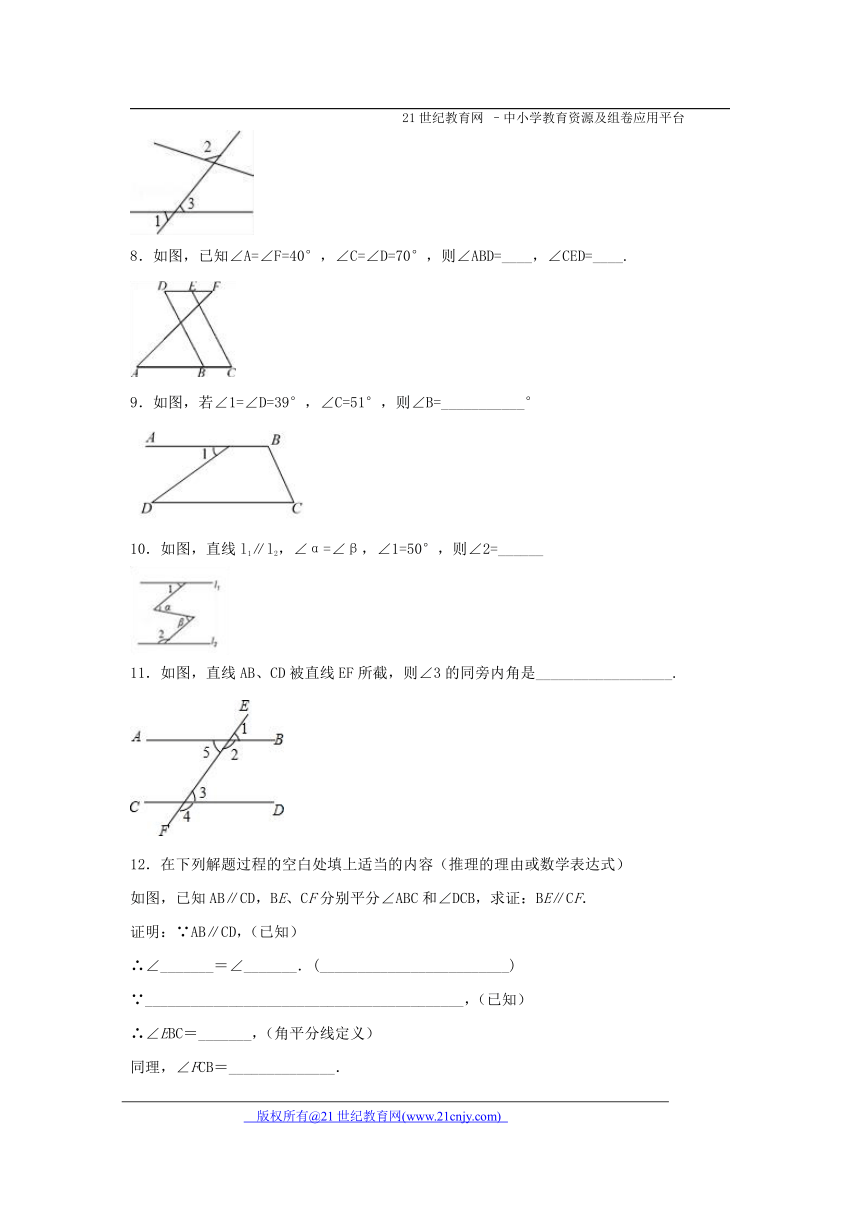
1.如图,直线AB、CD 与EF相交: 内错角有∠3与∠5,∠4与∠6;同旁内角有∠3与∠6,∠4与∠5;同位角有4组.
2.内错角相等,两直线平行;同旁内角互补,两直线平行.
基础知识和能力拓展训练
一、选择题
1.如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
A. ∠1=∠3 B. ∠2=∠4 C. ∠C=∠CBE D. ∠C+∠ABC=180
2.学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等;
②两直线平行,内错角相等;
③同位角相等,两直线平行;
④内错角相等,两直线平行.
A. ①② B. ②③ C. ③④ D. ①④
3.如图,描述同位角、内错角、同旁内角关系不正确的是( )
A. ∠1与∠4是同位角 B. ∠2与∠3是内错角
C. ∠3与∠4是同旁内角 D. ∠2与∠4是同旁内角
4.如图,下列选项中,不可以得到l1∥l2的是( )
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠5 D. ∠3+∠4=180°
5.如图,能判定EB∥AC的条件是( )
A. ∠A=∠ABE B. ∠A=∠EBD C. ∠C=∠ABC D. ∠C=∠ABE
6.如图所示,直线a 、b被直线c所截,现给出下列四种条件:①∠2=∠6 ②∠1=∠7 ③∠1+∠4=180° ④∠3=∠8,其中能推断a∥b的条件的序号是( )
A. ①② B. ①③ C. ①④ D. ③④
二、填空题
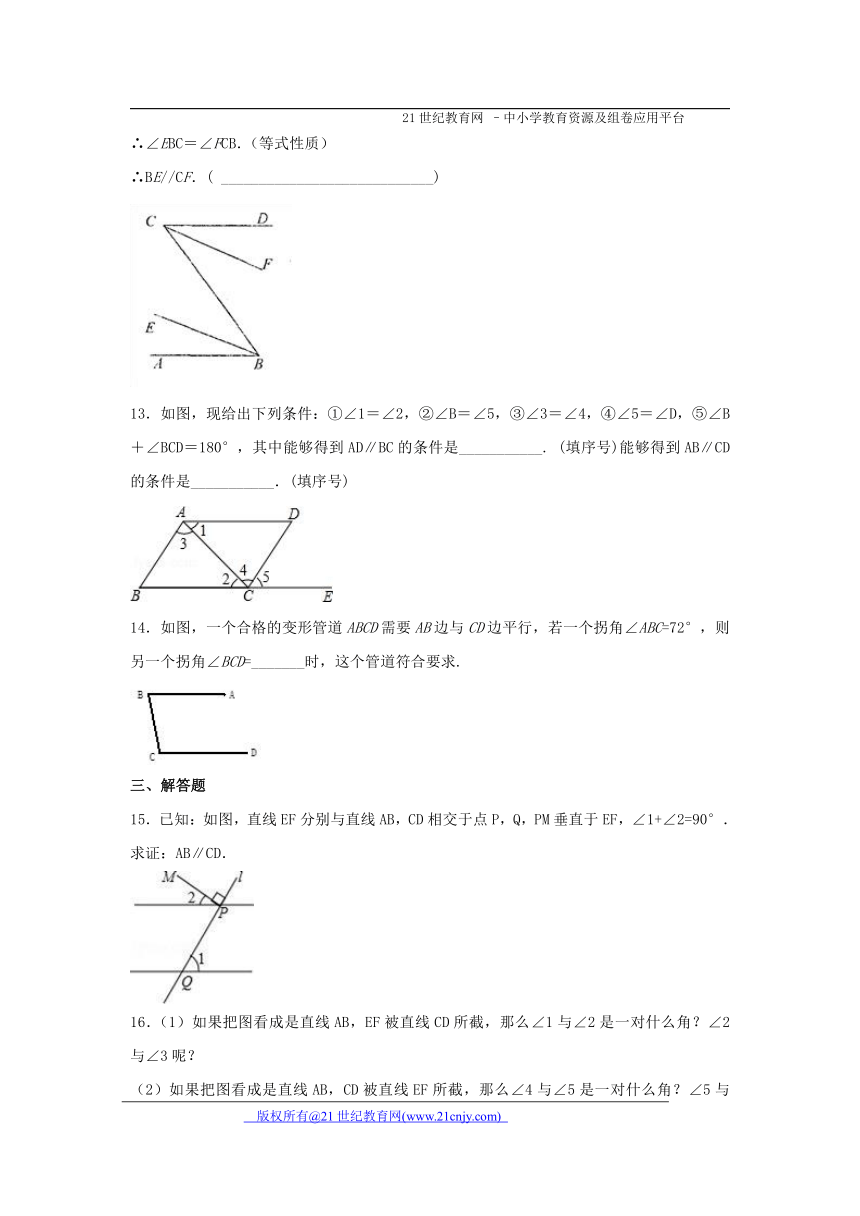
7.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .
8.如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=____,∠CED=____.
9.如图,若∠1=∠D=39°,∠C=51°,则∠B=___________°
10.如图,直线l1∥l2,∠α=∠β,∠1=50°,则∠2=______
11.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是__________________.
12.在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:∵AB∥CD,(已知)
∴∠_______=∠_______.(_________________________)
∵__________________________________________,(已知)
∴∠EBC=_______,(角平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( ____________________________)
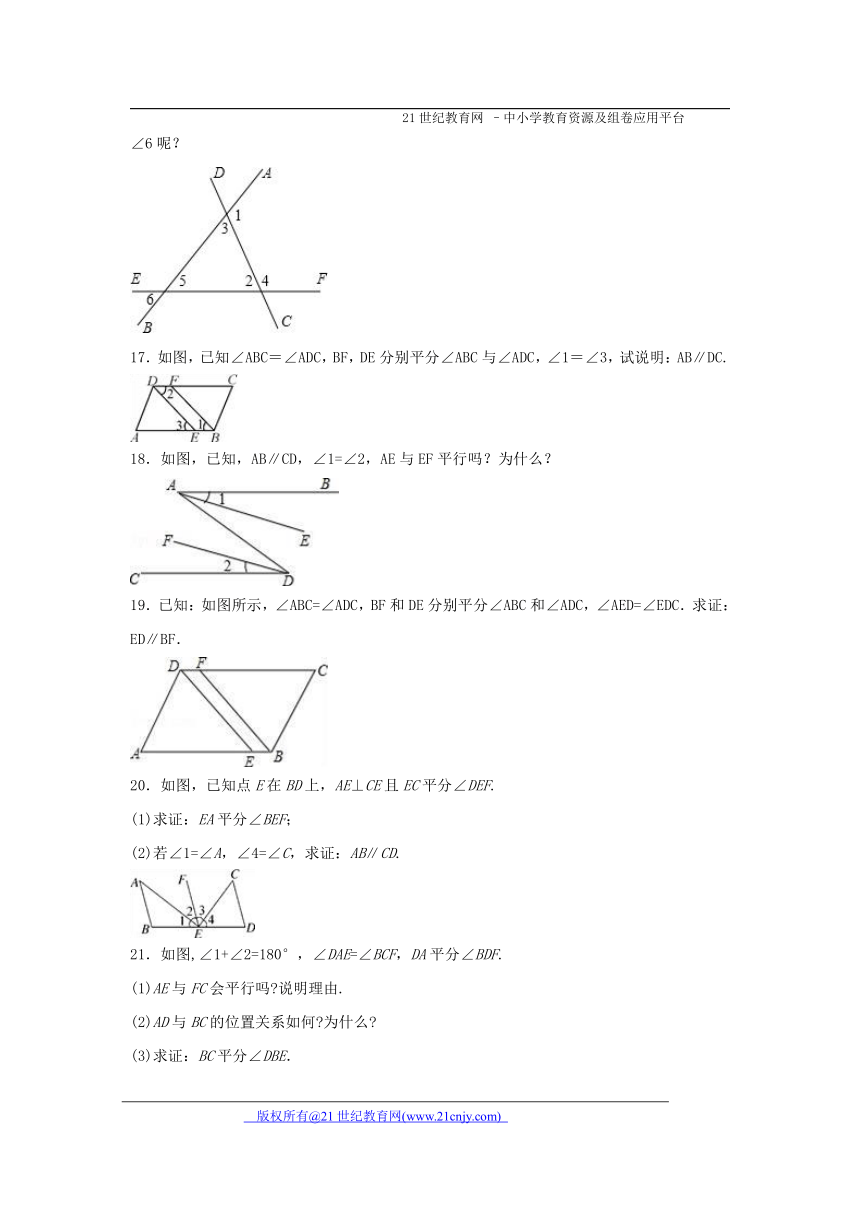
13.如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是___________. (填序号)能够得到AB∥CD的条件是___________.(填序号)
14.如图,一个合格的变形管道ABCD需要AB边与CD边平行,若一个拐角∠ABC=72°,则另一个拐角∠BCD=_______时,这个管道符合要求.
三、解答题
15.已知:如图,直线EF分别与直线AB,CD相交于点P,Q,PM垂直于EF,∠1+∠2=90°.
求证:AB∥CD.
16.(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角?∠2与∠3呢?
(2)如果把图看成是直线AB,CD被直线EF所截,那么∠4与∠5是一对什么角?∠5与∠6呢?
17.如图,已知∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,∠1=∠3,试说明:AB∥DC.
18.如图,已知,AB∥CD,∠1=∠2,AE与EF平行吗?为什么?
19.已知:如图所示,∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,∠AED=∠EDC.求证:ED∥BF.
20.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
21.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗 说明理由.
(2)AD与BC的位置关系如何 为什么
(3)求证:BC平分∠DBE.
参考答案
1.B
【解析】A. ∵∠1=∠3,∴AB∥CD, 故不正确;
B. ∵ ∠2=∠4 , ∴AD∥BC, 故正确;
C. ∵∠C=∠CBE , ∴AB∥CD, 故不正确;
D. ∵∠C+∠ABC=180 , ∴AB∥CD, 故不正确;
故选B.
2.C
【解析】试题解析:由作图过程可知, 为内错角相等, 为同位角相等.
可知小敏画平行线的依据有:③同位角相等,两直线平行;④内错角相等,两直线平行.
故选C.
3.D
【解析】解:A.∠1与∠4是同位角,故A选项正确;
B.∠2与∠3是内错角,故B选项正确;
C.∠3与∠4是同旁内角,故C选项正确;
D.∠2与∠4是同旁内角,故D选项错误.
故选D.
点睛:本题主要考查了同位角、内错角、同旁内角,解题的关键是熟记同位角、内错角、同旁内角的特征.
4.C
【解析】试卷分析:根据平行线的判定定理分别对各选项进行判断即可.
解:∵∠1=∠2,
∴l1∥l2(同位角相等 ,两直线平行);
∵∠2=∠3,
∴l1∥l2(内错角相等 ,两直线平行);
∵∠3+∠4=180°,
∴l1∥l2(同旁内角互补,两直线平行);
选项A、B、D均能得到l1∥l2.
而选项C中的∠3=∠5不能判断两直线平行.
故选C.
5.A
【解析】试题解析:A、∠A=∠ABE,根据内错角相等,两直线平行,可以得出EB∥AC,故本选项正确.
B、∠A=∠EBD不能判断出EB∥AC,故本选项错误;
C、∠C=∠ABC只能判断出AB=AC,不能判断出EB∥AC,故本选项错误;
D、∠C=∠ABE不能判断出EB∥AC,故本选项错误;
故选A.
6.A
【解析】试题解析:①∵∠2=∠6,
∴a∥b(同位角相等,两直线平行).
②∵∠2=∠8,∠6=∠8
∴∠2=∠6,
∴a∥b(同位角相等,两直线平行).
③∠1与∠4是邻补角不能判定两直线平行.
④∠3+∠8=180°,∠6=∠8
∴∠3+∠6=180°
∴a∥b(同旁内角互补,两直线平行),故∠3=∠8不能判定两直线平行.
故选A.
【点睛】本题考查了平行线的判定方法,难度适中,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
7.80°;80°;100°.
【解析】如图,已知∠2=100°,根据邻补角的定义和对顶角相等可得∠4=80°,∠5=100°,∠6=80°,再由同位角、内错角、同旁内角的定义可得∠3的同位角是∠6=80°,∠3的内错角是∠4=80°,∠3的同旁内角是∠5=100°.
8. 70° 110°
【解析】试题解析:∵∠A=∠F=40°,
∴DF∥AC,
∵∠D=70°,
∴∠D=∠ABD=70°,
∵DF∥AC,
∴∠CED+∠C=180°,
∵∠C=70°,
∴∠CED=110°.
点睛:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.
9.129°
【解析】∵∠1=∠D=39°,∴AB∥CD.
∵∠C=51°,∴∠B=180°-51°=129°.
10.130°
【解析】试题解析:如图,
∵l1∥l2,
∴∠3=∠1=50°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-50°=130°.
11.∠2
【解析】∵∠2与∠3都在直线AB、CD之间,且它们都在直线EF的同旁,
∴∠3的同旁内角是∠2,
故答案是:∠2.
12.答案见解析
【解析】证明:∵AB∥CD,(已知)
∴∠_ABC__=∠__DCB__.(__两直线平行,内错角相等__)
∵____ BE、CF分别平分∠ABC和∠DCB ___,(已知)
∴∠EBC=_∠ABC_,(角平分线定义)
同理,∠FCB=__∠DCB_,_.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( _内错角相等,两直线平行__)
13. ①④ ②③⑤
【解析】试题解析:①∵∠1=∠2,∴AD∥BC;
②∵∠B=∠5,∴AB∥CD;
③∵∠3=∠4,∴AB∥CD;
④∵∠5=∠D,∴AD∥BC;
⑤∵∠B+∠BCD=180°,∴AB∥CD.
∴能够得到AD∥BC的条件是①④; 能够得到AB∥CD的条件是②③⑤.
【点睛】本题考查的是平行线的判定,熟知同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解答此题的关键.
14.108°
【解析】∵当∠ABC+∠BCD=180°时,AB∥CD,
∴当∠BCD=180°-∠ABC=180°-72°-108°时,这个管道符合要求.
15.证明见解析.
【解析】试题分析:先根据垂直的定义得出∠APQ+∠2=90°,再由∠1+∠2=90°得出∠APQ=∠1,进而可得出结论.
试题解析:如图,
∵PM⊥EF(已知),
∴∠APQ+∠2=90°(垂直定义).
∵∠1+∠2=90°(已知),
∴∠APQ=∠1(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
16.(1)∠1与∠2是内错角,∠2与∠3是同旁内角;(2)∠4与∠5是同位角,∠5与∠6是对顶角.
【解析】试题分析:根据同位角、同旁内角、同位角、对顶角的定义进行判断即可.
试题解析:(1)观察图形,根据内错角的定义可知∠1与∠2是内错角,根据同旁内角的定义可知∠2与∠3是同旁内角;
(2)根据同位角的定义可知∠4与∠5是同位角,根据对顶角的定义可知∠5与∠6是对顶角.
17.见解析
【解析】试题分析:先根据角平分线定义可证明∠1=∠2,进而利用平行线的判定方法得出答案.
试题解析:证明:∵BF平分∠ABC,∴∠1=∠FBC.
∵DE平分∠ADC,∴∠2=∠ADE.
∵∠ABC=∠ADC,∴∠1+∠FBC=∠2+∠ADE,
∴2∠1=2∠2,即∠1=∠2.
又∵∠1=∠3,∴∠2=∠3,
∴AB∥DC.
18.AE∥DF,理由见解析.
【解析】试题分析:根据平行线的性质推出∠BAD=∠ADC,求出∠EAD=∠ADF,根据平行线的判定得出即可.
试题解析:AE∥DF,理由如下:
∵AB∥CD(已知),
∴∠BAD=∠ADC(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠BAD﹣∠1=∠ADC﹣∠2,
即∠EAD=∠ADF (等式的性质),
∴BE∥CF(内错角相等,两直线平行).
19.证明见解析.
【解析】试题分析:由于DE平分∠CDA,BF平分∠ABC,那么有∠1=∠2,∠4=∠5,而∠ABC=∠CDA,易得∠2=∠4,而∠2=∠3,于是∠3=∠4,从而可证DE∥BF.
试题解析:如图所示,
∵DE平分∠CDA,BF平分∠ABC,
∴∠1=∠2,∠4=∠5,
又∵∠ABC=∠CDA,
∴∠2=∠4,
∵∠2=∠3,
∴∠3=∠4,
∴DE∥BF.
20.(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由AE⊥CE易得∠2+∠3=90°且∠1+∠4=90°,由EC平分∠DEF易得∠3=∠4,从而∠1=∠2,故EA平分∠BEF;
(2)由(1)得∠3=∠4,进而得出EF∥DC,再利用AE⊥CE得出,∠1=∠2,进而得出AB∥CD.
试题解析:证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°.
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF.
(2)∵AE⊥CE,
∴∠AEC=90°,
∴∠1+∠4=90°.
∵∠1=∠A,∠4=∠C,
∴∠B+∠D=180°-2∠1+180°-2∠4=360°-2(∠1+∠4)=180°,
∴AB∥CD.
21.(1)平行,理由见解析;(2)平行,理由见解析;(3)证明见解析
【解析】试题分析:(1)证明∠1=∠CDB,利用同位角相等,两直线平行即可证得;
(2)平行,根据平行线的性质可以证得∠A=∠CBE,然后利用平行线的判定方法即可证得;
(3)∠EBC=∠CBD,根据平行线的性质即可证得.
试题解析:(1)平行,理由如下:
∵∠2+∠CDB=180°,∠1+∠2=180°,
∴∠CDB=∠1,∴AE∥FC.
(2)平行,理由如下:
∵AE∥FC,
∴∠CDA+∠DAE=180°,
∵∠DAE=∠BCF∴∠CDA+∠BCF=180°,
∴AD∥BC.
(3)平分,理由如下:
∵AE∥FC,
∴∠EBC=∠BCF,
∵AD∥BC,
∴∠BCF=∠FDA,∠DBC=∠BDA,
又∵DA平分∠BDF,即∠FDA=∠BDA,
∴∠EBC=∠DBC,
∴BC平分∠DBE
版权所有@21世纪教育网(www.21cnjy.com)
2.2探索直线平行的条件(2)同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
1.如图,直线AB、CD 与EF相交: 内错角有∠3与∠5,∠4与∠6;同旁内角有∠3与∠6,∠4与∠5;同位角有4组.
2.内错角相等,两直线平行;同旁内角互补,两直线平行.
基础知识和能力拓展训练
一、选择题
1.如图,点E在AB的延长线上,下列条件中能判断AD∥BC的是( )
A. ∠1=∠3 B. ∠2=∠4 C. ∠C=∠CBE D. ∠C+∠ABC=180
2.学行线后,小敏想出了过己知直线外一点画这条直线的平行线的新方法,她是通过折一张半透明的纸得到的(如图(1)~(4)),从图中可知,小敏画平行线的依据有( )
①两直线平行,同位角相等;
②两直线平行,内错角相等;
③同位角相等,两直线平行;
④内错角相等,两直线平行.
A. ①② B. ②③ C. ③④ D. ①④
3.如图,描述同位角、内错角、同旁内角关系不正确的是( )
A. ∠1与∠4是同位角 B. ∠2与∠3是内错角
C. ∠3与∠4是同旁内角 D. ∠2与∠4是同旁内角
4.如图,下列选项中,不可以得到l1∥l2的是( )
A. ∠1=∠2 B. ∠2=∠3 C. ∠3=∠5 D. ∠3+∠4=180°
5.如图,能判定EB∥AC的条件是( )
A. ∠A=∠ABE B. ∠A=∠EBD C. ∠C=∠ABC D. ∠C=∠ABE
6.如图所示,直线a 、b被直线c所截,现给出下列四种条件:①∠2=∠6 ②∠1=∠7 ③∠1+∠4=180° ④∠3=∠8,其中能推断a∥b的条件的序号是( )
A. ①② B. ①③ C. ①④ D. ③④
二、填空题
7.如图,如果∠1=40°,∠2=100°,那么∠3的同位角等于 ,∠3的内错角等于 ,∠3的同旁内角等于 .
8.如图,已知∠A=∠F=40°,∠C=∠D=70°,则∠ABD=____,∠CED=____.
9.如图,若∠1=∠D=39°,∠C=51°,则∠B=___________°
10.如图,直线l1∥l2,∠α=∠β,∠1=50°,则∠2=______
11.如图,直线AB、CD被直线EF所截,则∠3的同旁内角是__________________.
12.在下列解题过程的空白处填上适当的内容(推理的理由或数学表达式)
如图,已知AB∥CD,BE、CF分别平分∠ABC和∠DCB,求证:BE∥CF.
证明:∵AB∥CD,(已知)
∴∠_______=∠_______.(_________________________)
∵__________________________________________,(已知)
∴∠EBC=_______,(角平分线定义)
同理,∠FCB=______________.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( ____________________________)
13.如图,现给出下列条件:①∠1=∠2,②∠B=∠5,③∠3=∠4,④∠5=∠D,⑤∠B+∠BCD=180°,其中能够得到AD∥BC的条件是___________. (填序号)能够得到AB∥CD的条件是___________.(填序号)
14.如图,一个合格的变形管道ABCD需要AB边与CD边平行,若一个拐角∠ABC=72°,则另一个拐角∠BCD=_______时,这个管道符合要求.
三、解答题
15.已知:如图,直线EF分别与直线AB,CD相交于点P,Q,PM垂直于EF,∠1+∠2=90°.
求证:AB∥CD.
16.(1)如果把图看成是直线AB,EF被直线CD所截,那么∠1与∠2是一对什么角?∠2与∠3呢?
(2)如果把图看成是直线AB,CD被直线EF所截,那么∠4与∠5是一对什么角?∠5与∠6呢?
17.如图,已知∠ABC=∠ADC,BF,DE分别平分∠ABC与∠ADC,∠1=∠3,试说明:AB∥DC.
18.如图,已知,AB∥CD,∠1=∠2,AE与EF平行吗?为什么?
19.已知:如图所示,∠ABC=∠ADC,BF和DE分别平分∠ABC和∠ADC,∠AED=∠EDC.求证:ED∥BF.
20.如图,已知点E在BD上,AE⊥CE且EC平分∠DEF.
(1)求证:EA平分∠BEF;
(2)若∠1=∠A,∠4=∠C,求证:AB∥CD.
21.如图,∠1+∠2=180°,∠DAE=∠BCF,DA平分∠BDF.
(1)AE与FC会平行吗 说明理由.
(2)AD与BC的位置关系如何 为什么
(3)求证:BC平分∠DBE.
参考答案
1.B
【解析】A. ∵∠1=∠3,∴AB∥CD, 故不正确;
B. ∵ ∠2=∠4 , ∴AD∥BC, 故正确;
C. ∵∠C=∠CBE , ∴AB∥CD, 故不正确;
D. ∵∠C+∠ABC=180 , ∴AB∥CD, 故不正确;
故选B.
2.C
【解析】试题解析:由作图过程可知, 为内错角相等, 为同位角相等.
可知小敏画平行线的依据有:③同位角相等,两直线平行;④内错角相等,两直线平行.
故选C.
3.D
【解析】解:A.∠1与∠4是同位角,故A选项正确;
B.∠2与∠3是内错角,故B选项正确;
C.∠3与∠4是同旁内角,故C选项正确;
D.∠2与∠4是同旁内角,故D选项错误.
故选D.
点睛:本题主要考查了同位角、内错角、同旁内角,解题的关键是熟记同位角、内错角、同旁内角的特征.
4.C
【解析】试卷分析:根据平行线的判定定理分别对各选项进行判断即可.
解:∵∠1=∠2,
∴l1∥l2(同位角相等 ,两直线平行);
∵∠2=∠3,
∴l1∥l2(内错角相等 ,两直线平行);
∵∠3+∠4=180°,
∴l1∥l2(同旁内角互补,两直线平行);
选项A、B、D均能得到l1∥l2.
而选项C中的∠3=∠5不能判断两直线平行.
故选C.
5.A
【解析】试题解析:A、∠A=∠ABE,根据内错角相等,两直线平行,可以得出EB∥AC,故本选项正确.
B、∠A=∠EBD不能判断出EB∥AC,故本选项错误;
C、∠C=∠ABC只能判断出AB=AC,不能判断出EB∥AC,故本选项错误;
D、∠C=∠ABE不能判断出EB∥AC,故本选项错误;
故选A.
6.A
【解析】试题解析:①∵∠2=∠6,
∴a∥b(同位角相等,两直线平行).
②∵∠2=∠8,∠6=∠8
∴∠2=∠6,
∴a∥b(同位角相等,两直线平行).
③∠1与∠4是邻补角不能判定两直线平行.
④∠3+∠8=180°,∠6=∠8
∴∠3+∠6=180°
∴a∥b(同旁内角互补,两直线平行),故∠3=∠8不能判定两直线平行.
故选A.
【点睛】本题考查了平行线的判定方法,难度适中,正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键,不能遇到相等或互补关系的角就误认为具有平行关系,只有同位角相等、内错角相等、同旁内角互补,才能推出两被截直线平行.
7.80°;80°;100°.
【解析】如图,已知∠2=100°,根据邻补角的定义和对顶角相等可得∠4=80°,∠5=100°,∠6=80°,再由同位角、内错角、同旁内角的定义可得∠3的同位角是∠6=80°,∠3的内错角是∠4=80°,∠3的同旁内角是∠5=100°.
8. 70° 110°
【解析】试题解析:∵∠A=∠F=40°,
∴DF∥AC,
∵∠D=70°,
∴∠D=∠ABD=70°,
∵DF∥AC,
∴∠CED+∠C=180°,
∵∠C=70°,
∴∠CED=110°.
点睛:平行线的性质有:①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补.
9.129°
【解析】∵∠1=∠D=39°,∴AB∥CD.
∵∠C=51°,∴∠B=180°-51°=129°.
10.130°
【解析】试题解析:如图,
∵l1∥l2,
∴∠3=∠1=50°,
∵∠α=∠β,
∴AB∥CD,
∴∠2+∠3=180°,
∴∠2=180°-∠3=180°-50°=130°.
11.∠2
【解析】∵∠2与∠3都在直线AB、CD之间,且它们都在直线EF的同旁,
∴∠3的同旁内角是∠2,
故答案是:∠2.
12.答案见解析
【解析】证明:∵AB∥CD,(已知)
∴∠_ABC__=∠__DCB__.(__两直线平行,内错角相等__)
∵____ BE、CF分别平分∠ABC和∠DCB ___,(已知)
∴∠EBC=_∠ABC_,(角平分线定义)
同理,∠FCB=__∠DCB_,_.
∴∠EBC=∠FCB.(等式性质)
∴BE//CF.( _内错角相等,两直线平行__)
13. ①④ ②③⑤
【解析】试题解析:①∵∠1=∠2,∴AD∥BC;
②∵∠B=∠5,∴AB∥CD;
③∵∠3=∠4,∴AB∥CD;
④∵∠5=∠D,∴AD∥BC;
⑤∵∠B+∠BCD=180°,∴AB∥CD.
∴能够得到AD∥BC的条件是①④; 能够得到AB∥CD的条件是②③⑤.
【点睛】本题考查的是平行线的判定,熟知同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补,两直线平行是解答此题的关键.
14.108°
【解析】∵当∠ABC+∠BCD=180°时,AB∥CD,
∴当∠BCD=180°-∠ABC=180°-72°-108°时,这个管道符合要求.
15.证明见解析.
【解析】试题分析:先根据垂直的定义得出∠APQ+∠2=90°,再由∠1+∠2=90°得出∠APQ=∠1,进而可得出结论.
试题解析:如图,
∵PM⊥EF(已知),
∴∠APQ+∠2=90°(垂直定义).
∵∠1+∠2=90°(已知),
∴∠APQ=∠1(同角的余角相等),
∴AB∥CD(内错角相等,两直线平行).
16.(1)∠1与∠2是内错角,∠2与∠3是同旁内角;(2)∠4与∠5是同位角,∠5与∠6是对顶角.
【解析】试题分析:根据同位角、同旁内角、同位角、对顶角的定义进行判断即可.
试题解析:(1)观察图形,根据内错角的定义可知∠1与∠2是内错角,根据同旁内角的定义可知∠2与∠3是同旁内角;
(2)根据同位角的定义可知∠4与∠5是同位角,根据对顶角的定义可知∠5与∠6是对顶角.
17.见解析
【解析】试题分析:先根据角平分线定义可证明∠1=∠2,进而利用平行线的判定方法得出答案.
试题解析:证明:∵BF平分∠ABC,∴∠1=∠FBC.
∵DE平分∠ADC,∴∠2=∠ADE.
∵∠ABC=∠ADC,∴∠1+∠FBC=∠2+∠ADE,
∴2∠1=2∠2,即∠1=∠2.
又∵∠1=∠3,∴∠2=∠3,
∴AB∥DC.
18.AE∥DF,理由见解析.
【解析】试题分析:根据平行线的性质推出∠BAD=∠ADC,求出∠EAD=∠ADF,根据平行线的判定得出即可.
试题解析:AE∥DF,理由如下:
∵AB∥CD(已知),
∴∠BAD=∠ADC(两直线平行,内错角相等),
又∵∠1=∠2(已知),
∴∠BAD﹣∠1=∠ADC﹣∠2,
即∠EAD=∠ADF (等式的性质),
∴BE∥CF(内错角相等,两直线平行).
19.证明见解析.
【解析】试题分析:由于DE平分∠CDA,BF平分∠ABC,那么有∠1=∠2,∠4=∠5,而∠ABC=∠CDA,易得∠2=∠4,而∠2=∠3,于是∠3=∠4,从而可证DE∥BF.
试题解析:如图所示,
∵DE平分∠CDA,BF平分∠ABC,
∴∠1=∠2,∠4=∠5,
又∵∠ABC=∠CDA,
∴∠2=∠4,
∵∠2=∠3,
∴∠3=∠4,
∴DE∥BF.
20.(1)证明见解析;(2)证明见解析.
【解析】试题分析:(1)由AE⊥CE易得∠2+∠3=90°且∠1+∠4=90°,由EC平分∠DEF易得∠3=∠4,从而∠1=∠2,故EA平分∠BEF;
(2)由(1)得∠3=∠4,进而得出EF∥DC,再利用AE⊥CE得出,∠1=∠2,进而得出AB∥CD.
试题解析:证明:(1)∵AE⊥CE,
∴∠AEC=90°,
∴∠2+∠3=90°且∠1+∠4=90°.
又∵EC平分∠DEF,
∴∠3=∠4,
∴∠1=∠2,
∴EA平分∠BEF.
(2)∵AE⊥CE,
∴∠AEC=90°,
∴∠1+∠4=90°.
∵∠1=∠A,∠4=∠C,
∴∠B+∠D=180°-2∠1+180°-2∠4=360°-2(∠1+∠4)=180°,
∴AB∥CD.
21.(1)平行,理由见解析;(2)平行,理由见解析;(3)证明见解析
【解析】试题分析:(1)证明∠1=∠CDB,利用同位角相等,两直线平行即可证得;
(2)平行,根据平行线的性质可以证得∠A=∠CBE,然后利用平行线的判定方法即可证得;
(3)∠EBC=∠CBD,根据平行线的性质即可证得.
试题解析:(1)平行,理由如下:
∵∠2+∠CDB=180°,∠1+∠2=180°,
∴∠CDB=∠1,∴AE∥FC.
(2)平行,理由如下:
∵AE∥FC,
∴∠CDA+∠DAE=180°,
∵∠DAE=∠BCF∴∠CDA+∠BCF=180°,
∴AD∥BC.
(3)平分,理由如下:
∵AE∥FC,
∴∠EBC=∠BCF,
∵AD∥BC,
∴∠BCF=∠FDA,∠DBC=∠BDA,
又∵DA平分∠BDF,即∠FDA=∠BDA,
∴∠EBC=∠DBC,
∴BC平分∠DBE
版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
