2.3 平行线的性质（1）同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
2.3平行线的性质（1）同步练习
姓名：__________班级：__________学号：__________
本节应掌握和应用的知识点
两直线平行同位角相等 ;
两直线平行,内错角相等;
两直线平行,同旁内角互补 ．
基础知识和能力拓展训练
一、选择题
1．如图，从A处出发沿北偏东60°方向行走至B处，又沿北偏西20°方向行走至C处，则∠ABC的度数是( ) ．21·cn·jy·com
( http: / / www.21cnjy.com / )
A. 80° B. 90° C. 100° D. 95°
2．如图，将等腰直角三角板的直角顶点放在直尺的一边上，若∠1=70°，则∠2的度数为（　　）
( http: / / www.21cnjy.com / )
A. 95° B. 105° C. 115° D. 125°
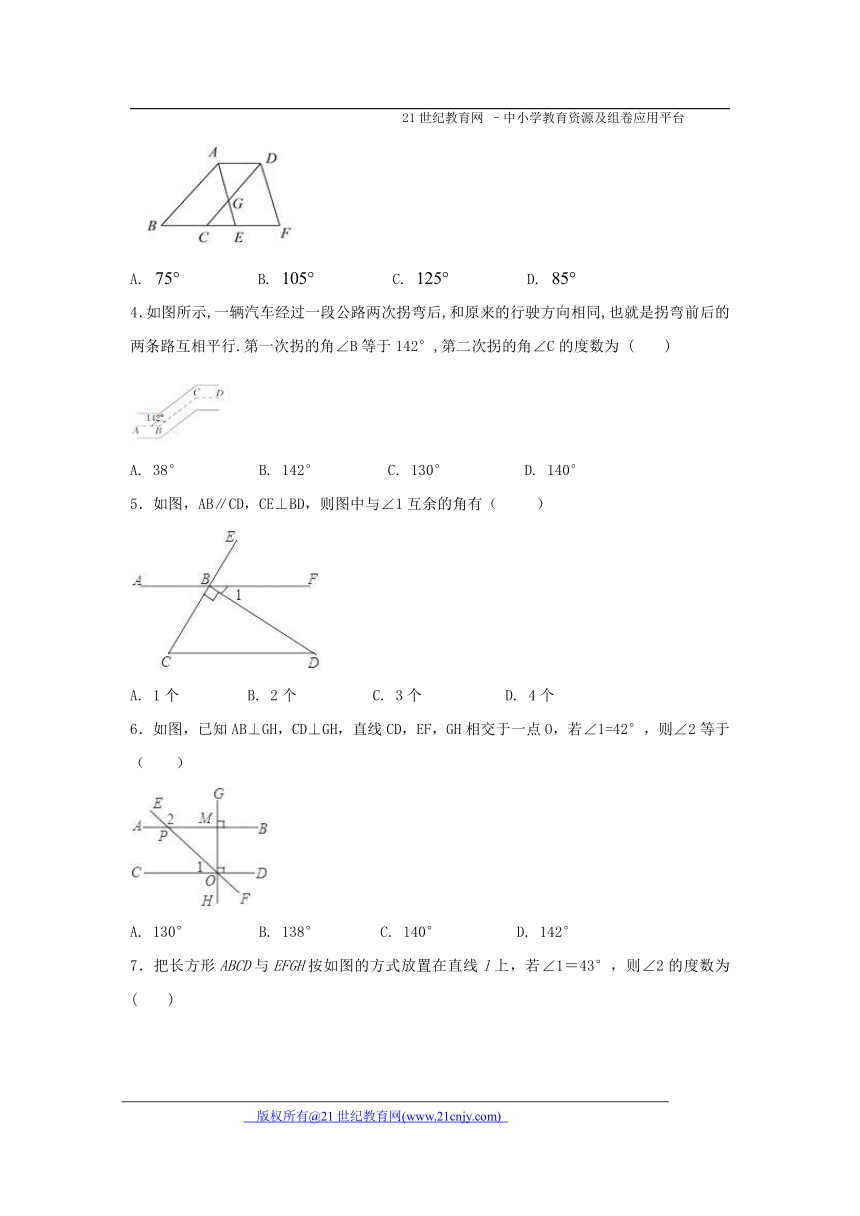
3．如图，将向右平移得到， 与交于点，其中， ，则（ ）．
( http: / / www.21cnjy.com / )
A. B. C. D.
4．如图所示,一辆汽车经过一段公路两次拐 ( http: / / www.21cnjy.com )弯后,和原来的行驶方向相同,也就是拐弯前后的两条路互相平行.第一次拐的角∠B等于142°,第二次拐的角∠C的度数为 (　　)
( http: / / www.21cnjy.com / )
A. 38° B. 142° C. 130° D. 140°
5．如图，AB∥CD，CE⊥BD，则图中与∠1互余的角有（ ）
( http: / / www.21cnjy.com / )
A. 1个 B. 2个 C. 3个 D. 4个
6．如图，已知AB⊥GH，CD⊥GH，直线CD，EF，GH相交于一点O，若∠1=42°，则∠2等于（　　）2·1·c·n·j·y
( http: / / www.21cnjy.com / )
A. 130° B. 138° C. 140° D. 142°
7．把长方形ABCD与EFGH按如图的方式放置在直线l上，若∠1＝43°，则∠2的度数为(　　)
( http: / / www.21cnjy.com / )
A. 43° B. 47° C. 37° D. 53°
8．如图所示,AB∥CD,P为AB,CD之间的一点,已知∠1=32°,∠2=25°,∠BPC的度数为 (　　)www-2-1-cnjy-com
( http: / / www.21cnjy.com / )
A. 57° B. 47° C. 58° D. 42°
9．如图，AB∥CD∥EF，则下列各式中正确的是（ ）
( http: / / www.21cnjy.com / )
A. ∠1+∠3=180° B. ∠1+∠2=∠3
C. ∠2+∠3+∠1=180° D. ∠2+∠3﹣∠1=180°
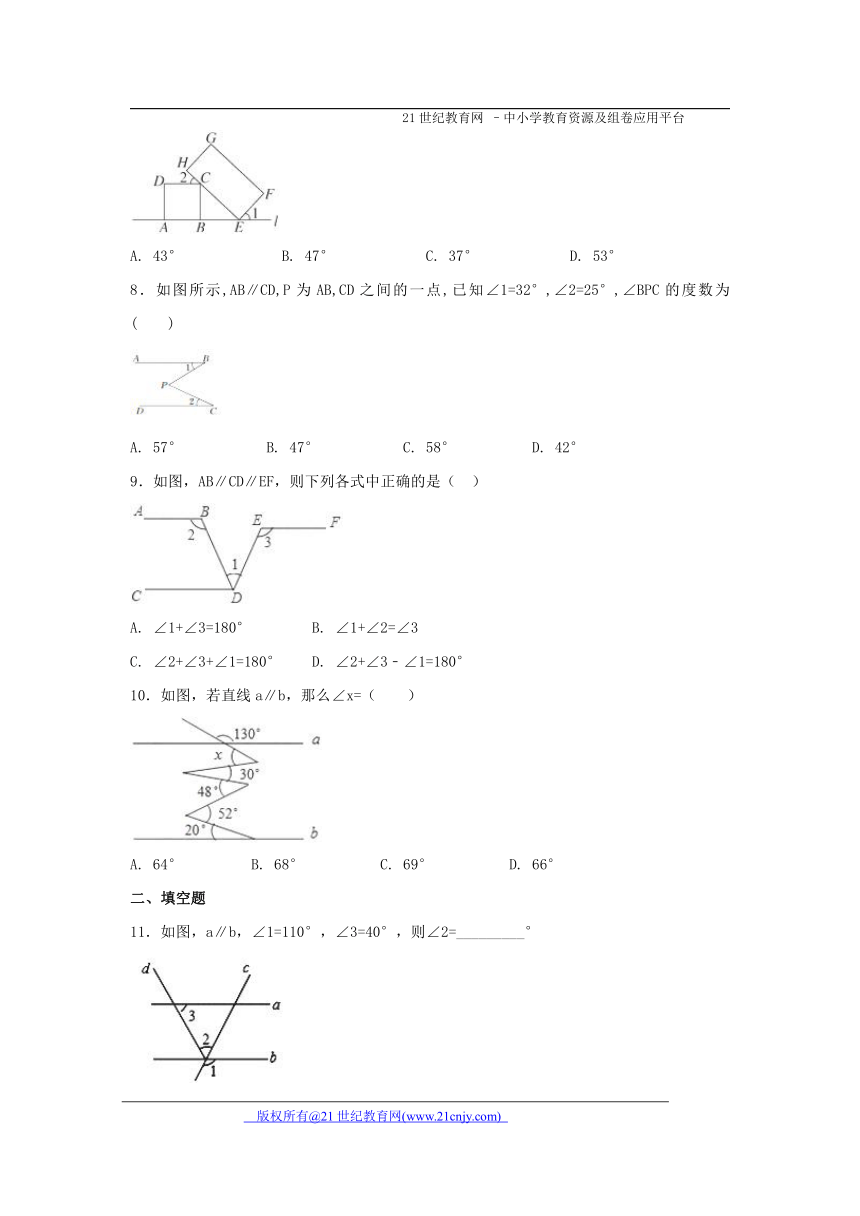
10．如图，若直线a∥b，那么∠x=（　　）
( http: / / www.21cnjy.com / )
A. 64° B. 68° C. 69° D. 66°
二、填空题
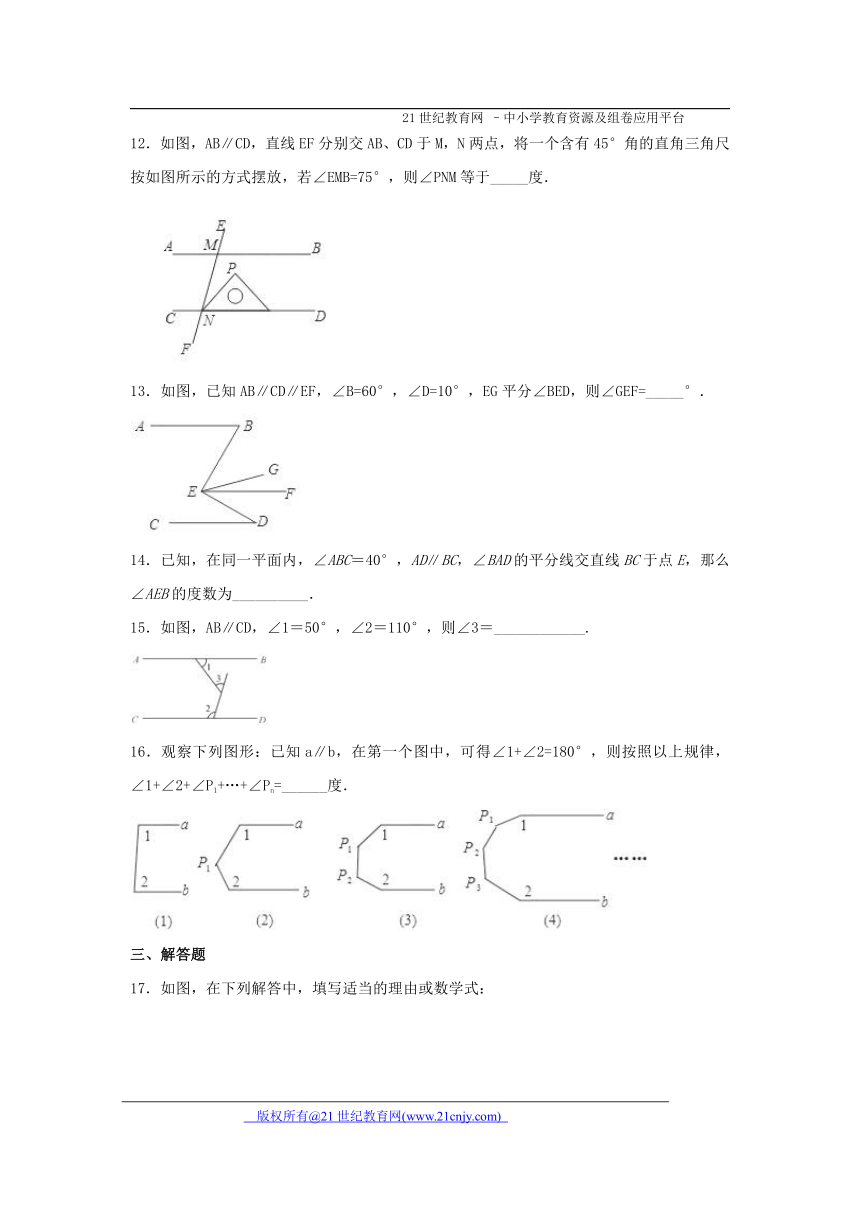
11．如图，a∥b，∠1=110°，∠3=40°，则∠2=_________°
( http: / / www.21cnjy.com / )
12．如图，AB∥CD，直线EF分别交AB ( http: / / www.21cnjy.com )、CD于M，N两点，将一个含有45°角的直角三角尺按如图所示的方式摆放，若∠EMB=75°，则∠PNM等于_____度．【出处：21教育名师】
( http: / / www.21cnjy.com / )
13．如图，已知AB∥CD∥EF，∠B=60°，∠D=10°，EG平分∠BED，则∠GEF=_____°．
( http: / / www.21cnjy.com / )
14．已知，在同一平面内，∠ABC＝40°，AD∥BC，∠BAD的平分线交直线BC于点E，那么∠AEB的度数为__________．21教育名师原创作品
15．如图，AB∥CD，∠1＝50°，∠2＝110°，则∠3＝____________.
( http: / / www.21cnjy.com / )
16．观察下列图形：已知a∥b，在第一个图中，可得∠1+∠2=180°，则按照以上规律，∠1+∠2+∠P1+…+∠Pn=______度．
( http: / / www.21cnjy.com / )
三、解答题
17．如图，在下列解答中，填写适当的理由或数学式：
( http: / / www.21cnjy.com / )
（1）∵ ∠ABD=∠CDB， （ 已知 ）
∴ ∥ . （ ）
（2）∵ ∠ADC+∠DCB=180°， （ 已知 ）
∴ ∥ . （ ）
（3）∵ AD∥BE， （ 已知 ）
∴ ∠DCE=∠ . （ ）
（4）∵ ∥ ， （ 已知 ）
∴ ∠BAE=∠CFE. （ ）
18．如图，AB∥CD，直线EF分别交AB，CD于点E，F，FG平分∠EFD，若∠1＝110°，求∠2的度数．
( http: / / www.21cnjy.com / )
19．如图， 中，点在边上， ⊥， ⊥，垂足分别是、，∠1＝∠2.
（1）与平行吗？为什么？
（2）若∠＝51°，∠＝54°，求∠的度数．
( http: / / www.21cnjy.com / )
20．如图：AB∥CD，直线l交AB、CD分别于点E、F，点M在EF上，N是直线CD上的一个动点（点N不与F重合）
（1）当点N在射线FC上运动时，∠FMN+∠FNM=∠AEF，说明理由；
（2）当点N在射线FD上运动时，∠FMN+∠FNM与∠AEF有什么关系并说明理由．
( http: / / www.21cnjy.com / )
21．（10分）如图，AB//CD，AE平分MAB交CD于点F，NF⊥CD，垂足为点F，
( http: / / www.21cnjy.com / )
(1)求证：CAF=EFD
(2)若MCD=80 ，求NFE的度数。
22．如图1，直线AB∥CD，直线l与直线 ( http: / / www.21cnjy.com )AB、CD相交于点E、F，点P是射线EA上的一个动点（不包括端点E），将△EPF沿PF折叠，使顶点E落在点Q处.
⑴ 若∠PEF=48°，点Q恰好落在其中的一条平行线上，请直接写出∠EFP的度数.
⑵ 若∠PEF＝75°，∠CFQ＝∠PFC，求∠EFP的度数.
( http: / / www.21cnjy.com / )
23．长江汛期即将来临，防 ( http: / / www.21cnjy.com )汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图，灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是a°/秒，灯B转动的速度是b°/秒，且a、b满足|a﹣3b|+（a+b﹣4）2=0．假定这一带长江两岸河堤是平行的，即PQ∥MN，且∠BAN=45°.
（1）求a、b的值；
（2）若灯B射线先转动20秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？
（3）如图，两灯同时转动，在灯A射线到 ( http: / / www.21cnjy.com )达AN之前．若射出的光束交于点C，过C作CD⊥AC交PQ于点D，则在转动过程中，∠BAC与∠BCD的数量关系是否发生变化？若不变，请求出其数量关系；若改变，请求出其取值范围．
( http: / / www.21cnjy.com / )
参考答案
1．C
【解析】试题解析：∵向北方向线是平行的，
∴∠A+∠ABF=180°，
∴∠ABF=180°-60°=120°，
∴∠ABC=∠ABF-∠CBF=120°-20°=100°，
故选C．
2．C
【解析】 ( http: / / www.21cnjy.com / )
∵∠1=70°，∠4=45°，
∴∠3=70°+45°=115°.
∵a∥b,
∴∠2=∠3=115°.
故选C.
3．B
【解析】∵△ABE向右平移得到△DCF,
∴AB∥CD,AE∥DF,
∴∠DCF=∠B=45°,
∴∠CDF=180°-45°-60°=75°,
∴∠AGC=180°-75°=105°
故选B.
4．B
【解析】试题分析：∵拐弯前后的两条路互相平行，
∴∠C＝∠B＝142°（两直线平行，内错角相等）．
故选B．
5．C
【解析】解：∵AB∥CD，
∴∠1=∠D.
∵∠C+∠D=90°,
∴∠C+∠1=90°;
∵∠EBF+∠1=90°, ∠EBF=∠ABC,
∴∠ABC+∠1=90°;
∴图中与∠1互余的角有3个，
故选C.
6．B
【解析】试题解析：如图：
( http: / / www.21cnjy.com / )
∵AB⊥GH，CD⊥GH，
∴∠GMB=∠GOD=90°，
∴AB∥CD，
∴∠BPF=∠1=42°，
∴∠2=180°-∠BPF=180°-42°=138°，
故选B．21cnjy.com
7．B
【解析】试题分析：∵∠1＝43°，∠HEF＝90°，
∴∠CEB＝47°，
∵CD∥AB，
∴∠2＝∠CEB＝47°，
故选：B．
8．A
【解析】试题分析：如图，过点P作PE∥AB，
( http: / / www.21cnjy.com / )
∵PE∥AB，
∴∠BPE＝∠1＝32°，
∵PE∥AB，AB∥CD，
∴PE∥CD，
∴∠CPE＝∠2＝25°，
∴∠BPC＝∠BPE＋∠CPE
＝32°＋25°
＝57°，
故选A．
点睛：本题主要考查了平行公理的推论和平行线的性质，正确地作出辅助线是解决此题的关键．
9．D
【解析】∵AB∥CD，
∴∠2+∠BDC=180°,即∠BDC=180° ∠2，
∵EF∥CD，
∴∠BDC+∠1=∠3，即∠BDC=∠3 ∠1，
∴180° ∠2=∠3 ∠1,即∠2+∠3=180°+∠1，
故选：D.
10．A
【解析】试题解析：令与130°互补的角为∠1，如图所示．
( http: / / www.21cnjy.com / )
∵∠1+130°=180°，
∴∠1=50°．
∵a∥b，
∴x+48°+20°=∠1+30°+52°，
∴x=64°．
故选A.
【点睛】本题考查了平行线的性质、平 ( http: / / www.21cnjy.com )行线间的折线问题以及角的计算，解题的关键是：利用“两平行线间的折线所成的角之间的关系-左边角之和等于右边角之和”规律做题．
11．70°
【解析】试题解析：如图，
( http: / / www.21cnjy.com / )
∵a∥b，∠3=40°，
∴∠4=∠3=40°．
∵∠1=∠2+∠4=110°，
∴∠2=110°-∠4=110°-40°=70°．
故答案为：70．
12．30
【解析】试题解析： ,
故答案为：30.
13．25
【解析】∵AB∥CD∥EF，∠B=60°，∠D=10°，
∴∠B=∠BEF=60°，∠CDE=∠FED=10°，
∴∠BED=∠BEF+∠FED=70°，
又∵EG平分∠BED，
∴∠GED=35°=∠FED+∠GEF，
∴∠GEF=25°，
故答案为：25．
14．70°或20°
【解析】试题解析：i).如图1，
( http: / / www.21cnjy.com / )
∵AD∥BC
∴∠BAD+∠ABC=180°
∵∠ABC＝40°
∴∠BAD=180°-40°=140°
∵AE是∠BAD的平分线
∴∠BAE=∠BAD=×140°=70°
ii).如图2，
( http: / / www.21cnjy.com / )
∵AD∥BC
∴∠BAD=∠ABC
∵∠ABC＝40°
∴∠BAD=40°
∵AE是∠BAD的平分线
∴∠BAE=∠BAD=×40°=20°
故∠BAE=70°或20°.
15．60°
【解析】试题解析：如图，
( http: / / www.21cnjy.com / )
∵∠2=110°，
∴∠4=70°，
∵AB∥CD，
∴∠5=∠1=50°，
∴∠3=180°-∠4-∠5=60°．
故选A．21教育网
点睛：两直线平行，同旁内角互补．
16．（n﹣1）×180
【解析】如图，
( http: / / www.21cnjy.com / )
分别过P1、P2、P3作直线AB的 ( http: / / www.21cnjy.com )平行线P1E，P2F，P3G，
∵AB∥CD，
∴AB∥P1E∥P2F∥P3G．
由平行线的性质可得出：∠1+∠3=180°，∠5+∠6=180°，∠7+∠8=180°，∠4+∠2=180°
∴（1）∠1+∠2=180°，【来源：21·世纪·教育·网】
（2）∠1+∠P1+∠2=2×180，
（3）∠1+∠P1+∠P2+∠2=3×180°，
（4）∠1+∠P1+∠P2+∠P3+∠2=4 ( http: / / www.21cnjy.com )×180°，
∴∠1+∠2+∠P1+…+∠Pn=（n+1）×180°．
故答案为：（n+1）×180．21·世纪*教育网
【点睛】分别过P1、P2、 ( http: / / www.21cnjy.com )P3作直线AB的平行线P1E，P2F，P3G，由平行线的性质可得出：∠1+∠3=180°，∠5+∠6=180°，∠7+∠8=180°，∠4+∠2=180°于是得到∠1+∠2=10°，∠1+∠P1+∠2=2×180，∠1+∠P1+∠P2+∠2=3×180°，∠1+∠P1+∠P2+∠P3+∠2=4×180°，根据规律得到结果∠1+∠2+∠P1+…+∠Pn=（n+1）×180°．2-1-c-n-j-y
17．答案见解析
【解析】试题分析：（1） ( http: / / www.21cnjy.com )根据内错角相等，两直线平行解答；（2）根据同旁内角互补，两直线平行解答；（3）根据两直线平行，内错角相等解答；（4）根据两直线平行，同位角相等解答.21*cnjy*com
（1）∵ ∠ABD=∠CDB， （ 已知 ）
∴ AB∥DC. （ 内错角相等，两直线平行 ）
（2）∵ ∠ADC+∠DCB=180°，（ 已知 ）
∴ AD∥BE . （ 同旁内角互补，两直线平行 ）
（3）∵ AD∥BE， （ 已知 ）
∴ ∠DCE=∠ADC . （ 两直线平行，内错角相等 ）
（4）∵ AB∥DC，（ 已知 ）
∴ ∠BAE=∠CFE. （ 两直线平行，同位角相等 ）
18．35°
【解析】试题分析：根据邻补角的定义求出∠3，根据两直线平行，内错角相等可得∠EFD=∠3，然后根据角平分线的定义可得∠4=∠EFD，再根据两直线平行，内错角相等可得∠2=∠4．
试题解析：如图，
( http: / / www.21cnjy.com / )
∵∠1=110°，
∴∠3=180°-∠1=180°-110°=70°，
∵FG平分∠EFD，
∴∠4=∠EFD=×70°=35°，
∵AB∥CD，
∴∠2=∠4=35°．【版权所有：21教育】
19．（1）平行（2）75°
【解析】试题分析：（1）根据平行线的判定推出AD∥EF，根据平行线的性质得出∠1=∠2=∠3，根据平行线的判定推出即可；21*cnjy*com
（2）由三角形内角和定理可求∠CAB，再由DG∥AB可得结论.
试题解析：（1）平行，理由如下：
∵EF⊥BC，AD⊥BC，∴∠BFE＝∠BDA＝90°，∴EF∥AD，∴∠2＝∠3，
∵∠1＝∠2，∴∠1＝∠3，∴DG∥AB.
（2）∵DG∥AB，∴∠CDG＝∠B＝51°，∵∠C＋∠CDG ＋∠CGD＝180°，∠C＝54°，
∴∠CGD＝180°-51°-54°＝75°．
点睛：平行线的性质有：①两直线平行，同位角相等，②两直线平行，内错角相等，③两直线平行，同旁内角互补，反之亦然．
20．（1）证明见解析；（2）∠FMN+∠FNM+∠AEF=180°，理由见解析.
【解析】试题分析:（1）利用两直线平行，同旁内角互补和三角形的内角和为180°，易得∠FMN+∠FNM=∠AEF；
（2）根据两直线平行，内错角相等和三角形的内角和为180°，易得∠FMN+∠FNM+∠AEF=180°．
解：（1）∵AB∥CD，
∴∠AEF+∠MFN=180°．
∵∠MFN+∠FMN+∠FNM=180°，
∴∠FMN+∠FNM=∠AEF．
（2）∠FMN+∠FNM+∠AEF=180°．
理由：∵AB∥CD，
∴∠AEF=∠MFN．
∵∠MFN+∠FMN+∠FNM=180°，
∴∠FMN+∠FNM+∠AEF=180°．
( http: / / www.21cnjy.com / )
21．(1)见解析；（2）见解析.
【解析】试题分析：（1）根据平行线的性质得到∠FAB=∠EFD （两直线平行，同位角相等），根据角平分线的定义得到∠CAF=∠FAB（角平分线的定义），等量代换得到∠CAF=∠EFD；
（2）根据角平分线的定义得到∠CAB=∠MCD=80°，根据角平分线的定义得到∠CAF=∠CAB＝40°，根据已知条件得到结论．
试题解析：
（1）证明：∵AB//CD（已知）
∴FAB=EFD （ 两直线平行，同位角相等 ）
∵AE平分MAB（已知）
∴CAF= FAB （ 角的平分线的定义 ）
∴CAF=EFD
（2）∵ AB//CD MCD=80
∴CAB=MCD=80
∵AE平分MAB
∴CAF=
由（1）有：EFD=CAF=40
∵ NF⊥CD
∴ NFE=
22．⑴ ∠EFP=42°或66°
⑵∠EFP的度数为35°或63°.
【解析】试题分析： HYPERLINK "http://www.21cnjy.com" 当点落在上，根据三角形的内角和即可得到结论；当点落在上，由折叠的性质得到垂直平分，得到，根据平行线的性质即可得到结论；
①如图，当点在平行线，之间时，设，由折叠可得根据平行线的性质即可得到结论；②如图，当点在的下方时，设 由得，.根据平行线的性质即可得到结论．【来源：21cnj*y.co*m】
试题解析： 或
ⅰ如图1，当点在平行线，之间时：
设的度数为，由折叠可得：
,
解得：
即：
( http: / / www.21cnjy.com / )
ⅱ如图2，当点在的下方时,
设
由得：
由折叠得
解得：
综上：的度数为或
23．（1）a=3，b=1；
（2）当t=10秒或85秒时，两灯的光束互相平行；
（3）2∠BAC=3∠BCD.
【解析】试题分析：（1）根据|a-3b ( http: / / www.21cnjy.com )|+（a+b-4）2=0，可得a-3b=0，且a+b-4=0，进而得出a、b的值；（2）设A灯转动x秒，两灯的光束互相平行，分两种情况进行讨论：①在灯A射线转到AN之前，②在灯A射线转到AN之后，分别求得t的值即可；（3）设灯A射线转动时间为t秒，根据∠BAC=45°-（180°-3t）=3t-135°，∠BCD=90°-∠BCA=90°-（180°-2t）=2t-90°，可得∠BAC与∠BCD的数量关系．21世纪教育网版权所有
试题解析：
(1)∵a、b满足|a 3b|+(a+b 4)2=0，
∴a 3b=0，且a+b 4=0，
∴a=3，b=1；
(2)设A灯转动x秒，两灯的光束互相平行，
①在灯A射线转到AN之前，
3t=(20+t)×1，
解得t=10；
②在灯A射线转到AN之后，
3t 3×60+(20+t)×1=180°，
解得t=85，
综上所述，当t=10秒或85秒时，两灯的光束互相平行；
(3)设灯A射线转动时间为t秒，
∵∠CAN=180° 3t，
∴∠BAC=45° (180° 3t)=3t 135°，
又∵PQ∥MN，
∴∠BCA=∠CBD+∠CAN=t+180° 3t=180° 2t，
而∠ACD=90°，
∴∠BCD=90° ∠BCA=90° (180° 2t)=2t 90°，
∴∠BAC:∠BCD=3:2，
即2∠BAC=3∠BCD.
点睛：本题主要考查了平行线的性质， ( http: / / www.21cnjy.com )非负数的性质以及角的和差关系的运用，解决问题的关键是运用分类的思想进行求解，解题时注意：任何一个数的绝对值都是非负数，当几个数或式子的绝对值相加得0时，则期中的每一项都必须等于0.www.21-cn-jy.com
( http: / / www.21cnjy.com / )
版权所有@21世纪教育网(www.21cnjy.com)