2.3 平行线的性质(2)同步练习
文档属性
| 名称 | 2.3 平行线的性质(2)同步练习 |

|
|
| 格式 | docx | ||
| 文件大小 | 432.7KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-09 00:00:00 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
2.3平行线的性质(2)同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
1. 平行线的性质与判定的综合:弄清平行线的性质与判定,并能利用平行线的性质和判定解题.
2.平行线的性质与判定的区别与联系:
(1)区别: 1)性质:根据两条直线平行,证角相等或互补.2)判定:根据两角相等或互补,证两条直线平行.
(2)联系:它们都是两条直 线被第三直线所截为前提;它们的条件和结论是互逆的.
(3)总 结:已知平行用性质,要证平行用判定.
基础知识和能力拓展训练
一、选择题
1.如图:∠1与∠2互补,需要具备的条件是( )
A. ∠1=∠3 B. ∠3+∠4=180° C. ∠3=∠4 D. ∠3+∠4=90°
2.如图,已知直线AB//CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为( ).
A. 120° B. 130° C. 150° D. 100°
3.如图,AB∥EF,CD⊥EF于点D,若∠BCD=140°,则∠ABC的度数为( )
A. 60° B. 50° C. 40° D. 30°
4.如图,已知∠1=∠2,则下列结论一定正确的是( )
A. ∠3=∠4 B. AB∥CD C. AD∥BC D. ∠B=∠D
5.如图,如果∠1+∠2=180°,那么( )
A. ∠2+∠4=180° B. ∠3+∠4=180° C. ∠1+∠3=180° D. ∠1=∠4
6.如图,下列推理错误的是( )
A. 因为∥,所以∠1=∠3
B. 因为∠2=∠4,所以∥
C. 因为∥,所以∠2=∠4
D. 因为∠1=∠3,∠2=∠4,所以∥
7.如图, AB∥EF, ,则、、的关系为( ).
A. B.
C. D. 不存在
8.如图,AB,CD,EF,MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
A. 35° B. 40° C. 45° D. 50°
9.如图,已知∠1=120°,∠2=60°,∠4=125°,则∠3的度数为( )
A. 120° B. 55° C. 60° D. 125°
10.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯的角∠A是110°,第二次拐弯的角∠B是150°,第三次拐弯的角是∠C,这时道路恰好和第一次拐弯之前的道路平行,则∠C是( )
A. 1200 B. 1300 C. 1400 D. 1500
二、填空题
11.如图,直线,将含有角的三角板的直角顶点放在直线上,若,则的度数为________
12.如图,两直线AB与CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=________°.
13.如图,若∠1=∠2,∠=,则∠的度数是_______.
三、解答题
14.如图,已知, , ,试说明:BE∥CF.
完善下面的解答过程,并填写理由或数学式:
解:∵ (已知)
∴AE∥ ( )
∴( )
∵(已知)
∴ ( )
∴DC∥AB( )
∴( )
即
∵(已知)
∴( )
即
∴BE∥CF( ) .
15.如图是明明设计的智力拼图玩具的一部分,现在明明遇到了两个问题,请你帮助解决:
问题1:∠D=32°,∠ACD=60°,为保证AB∥DE,则∠A等于多少度?
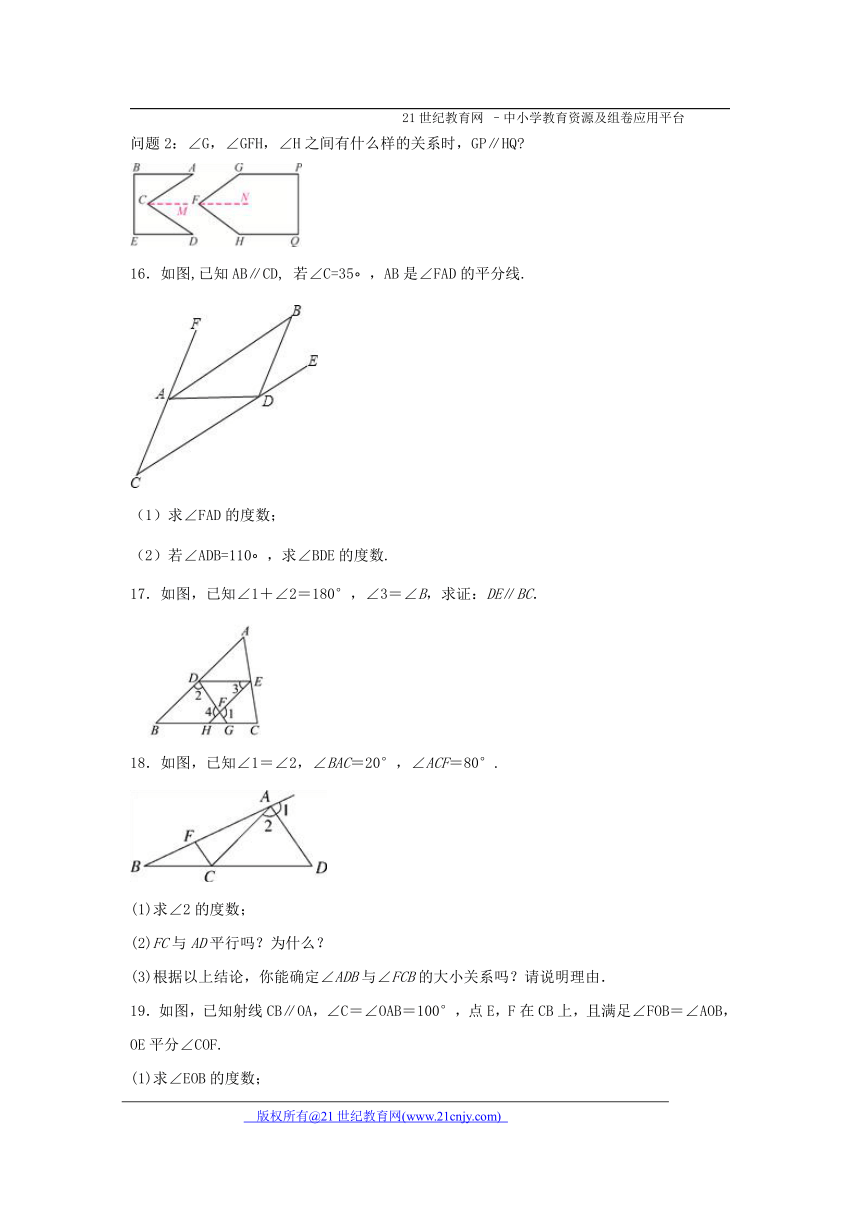
问题2:∠G,∠GFH,∠H之间有什么样的关系时,GP∥HQ
16.如图,已知AB∥CD, 若∠C=35 ,AB是∠FAD的平分线.
(1)求∠FAD的度数;
(2)若∠ADB=110 ,求∠BDE的度数.
17.如图,已知∠1+∠2=180°,∠3=∠B,求证:DE∥BC.
18.如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°.
(1)求∠2的度数;
(2)FC与AD平行吗?为什么?
(3)根据以上结论,你能确定∠ADB与∠FCB的大小关系吗?请说明理由.
19.如图,已知射线CB∥OA,∠C=∠OAB=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若向右平移AB,其他条件都不变,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值.
20.如图,AE∥CF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由;
(3)若AD平分∠BDF,试说明BC平分∠DBE.
参考答案
1.C
【解析】如图所示:
∵∠3=∠4,
∴a//b
∴∠1+∠2=180o,即∠1与∠2互补。
2.A
【解析】∵∠CDE=150o, ∠CDE+∠CDB=180o,
∴∠CDB=30o,
∵AB//CD,
∴∠ABD=∠CDB=30o, ∠ABC+∠C=180o,
∵BE平分∠ABC,
∴∠ABC=2∠ABD=60o,
又∵∠ABC+∠C=180o,
∴∠C=180o-∠ABC=(180-120)o=60 o;
故选A。
3.B
【解析】过点C作CG∥AB,
由题意可得:AB∥EF∥CG,
故∠B=∠BCG,
∵CD⊥EF于点D,
∴∠GCD=90°,
∵∠BCD=140°.
∴∠BCG=50°,
∴∠ABC=50°,
故选:B.
4.B
【解析】∵∠1=∠2
∴AB∥CD(内错角相等,两直线平行)
故选B.
5.C
【解析】∵∠1+∠2=180°,
∴AB∥CD,
∴∠2=∠4,∠3=∠4,
∵∠1+∠2=180°,∠2=∠3,
∴∠1+∠3=180°,
由邻补角定义得:∠1+∠4=180°,
故选C.
6.A
【解析】A选项:∠1和∠3不是AB和CD被截形成的角,不能证相等,故命题错误;
B选项:根据同位角相等两直线平行可证得AE∥CF,命题正确;
C选项:根据两直线平行,同位角相等即可征得∠2=∠4,命题正确;
D选项:∠1=∠3,∠2=∠4,则∠1+∠2=∠3+∠4,然后根据同位角相等两直线平行,可证得AB∥CD,命题正确.
故选A.
7.D
【解析】解:方法一:
延长交于,延长交于.
直角中, ; 中, .
因为,所以,于是,故.
故选.
方法二:
过点作,过点作,则由平行线的性质可得: , , ,∴,故,故选项.
点睛:本题考查通过构造辅助线,同时利用三角形外角的性质以及平行线的性质建立角之间的关系.
8.D
【解析】试卷分析:根据平行线的判定得出AB∥CD,根据平行线的性质得出∠BGP=∠GPC=80°,求出∠BGM=100°,则∠1根据角平分线定义求出即可.
解:∵∠2=∠3=70°,
∴AB∥CD,
∴∠BGP=∠GPC,
∵∠GPC=80°,
∴∠BGP=80°,
∴∠BGM=180° ∠BGP=100°,
∵GH平分∠MGB,
∴∠1=∠BGM=50°,
故选D.
9.D
【解析】如图所示:
∵∠5=∠2=60°(对顶角相等),
∴∠5+∠1=60°+120°=180°,
∴a∥b,
∴∠3=∠4=125°,
故选D.
10.C
【解析】试题分析:如图,首先过点B作BE∥AD,由AD∥CF,可得BE∥AD∥CF,然后根据两直线平行,内错角相等,两直线平行,同旁内角互补,即可求得∠C=140°.
点睛:此题考查了平行线的性质.此题难度不大,解题的关键是注意掌握两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用,注意数形结合思想的应用,注意辅助线的作法.
11.20
【解析】试题分析:过B作BE∥m,则根据平行公理及推论可知l∥BE,然后可证明得到∠1+∠2=∠ABC=45°,因此可求得∠2=20°.
故答案为:20.
12.900
【解析】试题解析:分别过E点,F点,G点,H点作 平行于AB,
利用内错角和同旁内角,把这六个角转化一下,可得有5个180°的角,
∴180×5=900°.
13.
【解析】∵∠1=∠2,
∴AD//BC,
∴∠+∠=180o,
又∵∠=,
∴∠=(180-78)o=.
故答案是: .
14.答案见解析.
【解析】试题分析:根据平行线的判定与性质,灵活判断同位角、内错角、同旁内角,逐步可求解.
试题解析:解:∵(已知)
∴AE∥ BC ( 内错角相等,两直线平行)
∴ ( 两直线平行,内错角相等)
∵(已知)
∴ ( 等量代换)
∴DC∥AB ( 同位角相等,两直线平行)
∴ ( 两直线平行,同旁内角互补)
即
∵(已知)
∴( 等量代换 )
即
∴BE∥CF ( 同旁内角互补,两直线平行 ) .
15.28°,∠G+∠GFH+∠H=360°
【解析】试题分析:(1)过C作CM∥AB,根据平行线的性质可得∠A=∠1=28°,再计算∠2=∠D=32°可得答案;
(2)当∠G+∠GFH+∠H=360°时,GP∥HQ;过F作FN∥GP,然后证明∠2+∠H=180°进而可得FN∥HQ,从而可证出GP∥HQ.
试题解析:(1)过点C作CM∥AB.
因为CM∥AB,所以∠ACM=∠A.
因为AB∥DE,
所以CM∥DE.所以∠DCM=∠D.
又因为∠ACD=60°,
所以∠ACM+∠DCM=60°.
所以∠ACM=60°-∠DCM=60°-∠D=60°-32°=28°.
所以∠A=28°时,AB∥DE.
(2)过点F作FN∥GP.
因为FN∥GP,
所以∠G+∠GFN=180°.
因为GP∥HQ,
所以FN∥HQ.所以∠H+∠NFH=180°.
所以∠G+∠GFH+∠H=∠G+∠GFN+∠H+∠NFH=180°+180°=360°.
所以∠G+∠GFH+∠H=360°时,GP∥HQ.
点睛: 此题主要考查了平行线的判定和性质,关键是掌握两直线平行,内错角相等,同旁内角互补.
16.(1)70°;(2)35°.
【解析】试题分析:(1)由AB//CD可得∠C=∠FAB=35°,再根据AB是∠FAD的平分线即可得;
(2)由AB//CD可得∠ADC=∠BAD=35°,再根据∠ADB=110°,利用平角的定义即可得.
试题解析:(1)∵AB//CD,
∴∠C=∠FAB=35°,
∵AB是∠FAD的平分线,
∴∠FAB=∠BAD=35°,
∴∠FAD=∠FAB+∠BAD=70°;
(2)∵AB//CD,
∴∠ADC=∠BAD=35°,
又∵∠ADB=110°,
∴∠BDE=180°-∠ADC- ∠ADB =180°-35°-110°=35°.
17.证明见解析.
【解析】要证明DE∥BC.需证明∠3=∠EHC.而证明∠3=∠EHC可通过证明EF∥AB及已知条件∠3=∠B进行推理即可.
证明:∵∠1+∠2=180°,∠1=∠4,
∴∠2+∠4=180°.
∴EH∥AB.
∴∠B=∠EHC.
∵∠3=∠B,
∴∠3=∠EHC.
∴DE∥BC.
18.(1) ∠2=80°;(2)答案见解析;(3) 答案见解析.
【解析】试题分析:(1)利用平角定义,根据题意确定出∠2的度数即可;
(2)FC与AD平行,理由为:利用内错角相等两直线平行即可得证;
(3)∠ADB=∠FCB,理由为:由FC与AD平行,利用两直线平行同位角相等即可得证.
试题解析:(1)∵∠1=∠2,∠BAC=20°,∠1+∠2+∠BAC=180°,
∴∠2=80°;
(2)∵∠2=∠ACF=80°,
∴FC∥AD;
(3)∠ADB=∠FCB,理由为:
证明:∵FC∥AD,
∴∠ADB=∠FCB.
19.(1)40°(2)这个比值不变,比值为1∶2
【解析】试题分析: 根据两直线平行,同旁内角互补求出,然后求出 计算即可得解;
根据两直线平行,内错角相等可得 再根据三角形的一个外角等于与它不相邻的两个内角的和可得即可得解;
试题解析:
(1)∵CB∥OA,
∵平分
(2)这个比值不变,比值为1∶2.理由:
∵CB∥OA,
20.见解析
【解析】试题分析:(1)由平行线的性质求得∠BDC=∠1=35°,然后由邻补角的定义求得∠2的度数即可;
(2)由平行线的性质可知:∠A+∠ADC=180°,然后由∵∠A=∠C,再证得∠C+∠ADC=180°,从而可证得BC∥AD;
(3)由AE∥CF可证明∠BDF=∠DBE,由BC∥AD,可证明∠ADB=∠DBC,由角平分线的定义可知,∠ADB=∠BDF,从而可证明∠DBC=∠EBD.
试题解析:(1)∵AE∥CF,
∴∠BDC=∠1=35°,
又∵∠2+∠BDC=180°,
∴∠2=180°-∠BDC=180°-35°=145°;
(2)BC∥AD.
理由:∵AE∥CF,∴∠A+∠ADC=180°,
又∵∠A=∠C,∴∠C+∠ADC=180°,
∴BC∥AD.
(3)∵AE∥CF,∴∠BDF=∠DBE.
∵BC∥AD,∴∠ADB=∠DBC.
∵AD平分∠BDF,∴∠ADB=∠BDF,∴∠DBC=∠EBD.
∴BC平分∠DBE.
版权所有@21世纪教育网(www.21cnjy.com)
2.3平行线的性质(2)同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
1. 平行线的性质与判定的综合:弄清平行线的性质与判定,并能利用平行线的性质和判定解题.
2.平行线的性质与判定的区别与联系:
(1)区别: 1)性质:根据两条直线平行,证角相等或互补.2)判定:根据两角相等或互补,证两条直线平行.
(2)联系:它们都是两条直 线被第三直线所截为前提;它们的条件和结论是互逆的.
(3)总 结:已知平行用性质,要证平行用判定.
基础知识和能力拓展训练
一、选择题
1.如图:∠1与∠2互补,需要具备的条件是( )
A. ∠1=∠3 B. ∠3+∠4=180° C. ∠3=∠4 D. ∠3+∠4=90°
2.如图,已知直线AB//CD,BE平分∠ABC,交CD于D,∠CDE=150°,则∠C的度数为( ).
A. 120° B. 130° C. 150° D. 100°
3.如图,AB∥EF,CD⊥EF于点D,若∠BCD=140°,则∠ABC的度数为( )
A. 60° B. 50° C. 40° D. 30°
4.如图,已知∠1=∠2,则下列结论一定正确的是( )
A. ∠3=∠4 B. AB∥CD C. AD∥BC D. ∠B=∠D
5.如图,如果∠1+∠2=180°,那么( )
A. ∠2+∠4=180° B. ∠3+∠4=180° C. ∠1+∠3=180° D. ∠1=∠4
6.如图,下列推理错误的是( )
A. 因为∥,所以∠1=∠3
B. 因为∠2=∠4,所以∥
C. 因为∥,所以∠2=∠4
D. 因为∠1=∠3,∠2=∠4,所以∥
7.如图, AB∥EF, ,则、、的关系为( ).
A. B.
C. D. 不存在
8.如图,AB,CD,EF,MN均为直线,∠2=∠3=70°,∠GPC=80°,GH平分∠MGB,则∠1=( )
A. 35° B. 40° C. 45° D. 50°
9.如图,已知∠1=120°,∠2=60°,∠4=125°,则∠3的度数为( )
A. 120° B. 55° C. 60° D. 125°
10.如图,一条公路修到湖边时,需拐弯绕湖而过,如果第一次拐弯的角∠A是110°,第二次拐弯的角∠B是150°,第三次拐弯的角是∠C,这时道路恰好和第一次拐弯之前的道路平行,则∠C是( )
A. 1200 B. 1300 C. 1400 D. 1500
二、填空题
11.如图,直线,将含有角的三角板的直角顶点放在直线上,若,则的度数为________
12.如图,两直线AB与CD平行,则∠1+∠2+∠3+∠4+∠5+∠6=________°.
13.如图,若∠1=∠2,∠=,则∠的度数是_______.
三、解答题
14.如图,已知, , ,试说明:BE∥CF.
完善下面的解答过程,并填写理由或数学式:
解:∵ (已知)
∴AE∥ ( )
∴( )
∵(已知)
∴ ( )
∴DC∥AB( )
∴( )
即
∵(已知)
∴( )
即
∴BE∥CF( ) .
15.如图是明明设计的智力拼图玩具的一部分,现在明明遇到了两个问题,请你帮助解决:
问题1:∠D=32°,∠ACD=60°,为保证AB∥DE,则∠A等于多少度?
问题2:∠G,∠GFH,∠H之间有什么样的关系时,GP∥HQ
16.如图,已知AB∥CD, 若∠C=35 ,AB是∠FAD的平分线.
(1)求∠FAD的度数;
(2)若∠ADB=110 ,求∠BDE的度数.
17.如图,已知∠1+∠2=180°,∠3=∠B,求证:DE∥BC.
18.如图,已知∠1=∠2,∠BAC=20°,∠ACF=80°.
(1)求∠2的度数;
(2)FC与AD平行吗?为什么?
(3)根据以上结论,你能确定∠ADB与∠FCB的大小关系吗?请说明理由.
19.如图,已知射线CB∥OA,∠C=∠OAB=100°,点E,F在CB上,且满足∠FOB=∠AOB,OE平分∠COF.
(1)求∠EOB的度数;
(2)若向右平移AB,其他条件都不变,那么∠OBC∶∠OFC的值是否随之变化?若变化,找出变化规律;若不变,求出这个比值.
20.如图,AE∥CF,∠A=∠C.
(1)若∠1=35°,求∠2的度数;
(2)判断AD与BC的位置关系,并说明理由;
(3)若AD平分∠BDF,试说明BC平分∠DBE.
参考答案
1.C
【解析】如图所示:
∵∠3=∠4,
∴a//b
∴∠1+∠2=180o,即∠1与∠2互补。
2.A
【解析】∵∠CDE=150o, ∠CDE+∠CDB=180o,
∴∠CDB=30o,
∵AB//CD,
∴∠ABD=∠CDB=30o, ∠ABC+∠C=180o,
∵BE平分∠ABC,
∴∠ABC=2∠ABD=60o,
又∵∠ABC+∠C=180o,
∴∠C=180o-∠ABC=(180-120)o=60 o;
故选A。
3.B
【解析】过点C作CG∥AB,
由题意可得:AB∥EF∥CG,
故∠B=∠BCG,
∵CD⊥EF于点D,
∴∠GCD=90°,
∵∠BCD=140°.
∴∠BCG=50°,
∴∠ABC=50°,
故选:B.
4.B
【解析】∵∠1=∠2
∴AB∥CD(内错角相等,两直线平行)
故选B.
5.C
【解析】∵∠1+∠2=180°,
∴AB∥CD,
∴∠2=∠4,∠3=∠4,
∵∠1+∠2=180°,∠2=∠3,
∴∠1+∠3=180°,
由邻补角定义得:∠1+∠4=180°,
故选C.
6.A
【解析】A选项:∠1和∠3不是AB和CD被截形成的角,不能证相等,故命题错误;
B选项:根据同位角相等两直线平行可证得AE∥CF,命题正确;
C选项:根据两直线平行,同位角相等即可征得∠2=∠4,命题正确;
D选项:∠1=∠3,∠2=∠4,则∠1+∠2=∠3+∠4,然后根据同位角相等两直线平行,可证得AB∥CD,命题正确.
故选A.
7.D
【解析】解:方法一:
延长交于,延长交于.
直角中, ; 中, .
因为,所以,于是,故.
故选.
方法二:
过点作,过点作,则由平行线的性质可得: , , ,∴,故,故选项.
点睛:本题考查通过构造辅助线,同时利用三角形外角的性质以及平行线的性质建立角之间的关系.
8.D
【解析】试卷分析:根据平行线的判定得出AB∥CD,根据平行线的性质得出∠BGP=∠GPC=80°,求出∠BGM=100°,则∠1根据角平分线定义求出即可.
解:∵∠2=∠3=70°,
∴AB∥CD,
∴∠BGP=∠GPC,
∵∠GPC=80°,
∴∠BGP=80°,
∴∠BGM=180° ∠BGP=100°,
∵GH平分∠MGB,
∴∠1=∠BGM=50°,
故选D.
9.D
【解析】如图所示:
∵∠5=∠2=60°(对顶角相等),
∴∠5+∠1=60°+120°=180°,
∴a∥b,
∴∠3=∠4=125°,
故选D.
10.C
【解析】试题分析:如图,首先过点B作BE∥AD,由AD∥CF,可得BE∥AD∥CF,然后根据两直线平行,内错角相等,两直线平行,同旁内角互补,即可求得∠C=140°.
点睛:此题考查了平行线的性质.此题难度不大,解题的关键是注意掌握两直线平行,内错角相等与两直线平行,同旁内角互补定理的应用,注意数形结合思想的应用,注意辅助线的作法.
11.20
【解析】试题分析:过B作BE∥m,则根据平行公理及推论可知l∥BE,然后可证明得到∠1+∠2=∠ABC=45°,因此可求得∠2=20°.
故答案为:20.
12.900
【解析】试题解析:分别过E点,F点,G点,H点作 平行于AB,
利用内错角和同旁内角,把这六个角转化一下,可得有5个180°的角,
∴180×5=900°.
13.
【解析】∵∠1=∠2,
∴AD//BC,
∴∠+∠=180o,
又∵∠=,
∴∠=(180-78)o=.
故答案是: .
14.答案见解析.
【解析】试题分析:根据平行线的判定与性质,灵活判断同位角、内错角、同旁内角,逐步可求解.
试题解析:解:∵(已知)
∴AE∥ BC ( 内错角相等,两直线平行)
∴ ( 两直线平行,内错角相等)
∵(已知)
∴ ( 等量代换)
∴DC∥AB ( 同位角相等,两直线平行)
∴ ( 两直线平行,同旁内角互补)
即
∵(已知)
∴( 等量代换 )
即
∴BE∥CF ( 同旁内角互补,两直线平行 ) .
15.28°,∠G+∠GFH+∠H=360°
【解析】试题分析:(1)过C作CM∥AB,根据平行线的性质可得∠A=∠1=28°,再计算∠2=∠D=32°可得答案;
(2)当∠G+∠GFH+∠H=360°时,GP∥HQ;过F作FN∥GP,然后证明∠2+∠H=180°进而可得FN∥HQ,从而可证出GP∥HQ.
试题解析:(1)过点C作CM∥AB.
因为CM∥AB,所以∠ACM=∠A.
因为AB∥DE,
所以CM∥DE.所以∠DCM=∠D.
又因为∠ACD=60°,
所以∠ACM+∠DCM=60°.
所以∠ACM=60°-∠DCM=60°-∠D=60°-32°=28°.
所以∠A=28°时,AB∥DE.
(2)过点F作FN∥GP.
因为FN∥GP,
所以∠G+∠GFN=180°.
因为GP∥HQ,
所以FN∥HQ.所以∠H+∠NFH=180°.
所以∠G+∠GFH+∠H=∠G+∠GFN+∠H+∠NFH=180°+180°=360°.
所以∠G+∠GFH+∠H=360°时,GP∥HQ.
点睛: 此题主要考查了平行线的判定和性质,关键是掌握两直线平行,内错角相等,同旁内角互补.
16.(1)70°;(2)35°.
【解析】试题分析:(1)由AB//CD可得∠C=∠FAB=35°,再根据AB是∠FAD的平分线即可得;
(2)由AB//CD可得∠ADC=∠BAD=35°,再根据∠ADB=110°,利用平角的定义即可得.
试题解析:(1)∵AB//CD,
∴∠C=∠FAB=35°,
∵AB是∠FAD的平分线,
∴∠FAB=∠BAD=35°,
∴∠FAD=∠FAB+∠BAD=70°;
(2)∵AB//CD,
∴∠ADC=∠BAD=35°,
又∵∠ADB=110°,
∴∠BDE=180°-∠ADC- ∠ADB =180°-35°-110°=35°.
17.证明见解析.
【解析】要证明DE∥BC.需证明∠3=∠EHC.而证明∠3=∠EHC可通过证明EF∥AB及已知条件∠3=∠B进行推理即可.
证明:∵∠1+∠2=180°,∠1=∠4,
∴∠2+∠4=180°.
∴EH∥AB.
∴∠B=∠EHC.
∵∠3=∠B,
∴∠3=∠EHC.
∴DE∥BC.
18.(1) ∠2=80°;(2)答案见解析;(3) 答案见解析.
【解析】试题分析:(1)利用平角定义,根据题意确定出∠2的度数即可;
(2)FC与AD平行,理由为:利用内错角相等两直线平行即可得证;
(3)∠ADB=∠FCB,理由为:由FC与AD平行,利用两直线平行同位角相等即可得证.
试题解析:(1)∵∠1=∠2,∠BAC=20°,∠1+∠2+∠BAC=180°,
∴∠2=80°;
(2)∵∠2=∠ACF=80°,
∴FC∥AD;
(3)∠ADB=∠FCB,理由为:
证明:∵FC∥AD,
∴∠ADB=∠FCB.
19.(1)40°(2)这个比值不变,比值为1∶2
【解析】试题分析: 根据两直线平行,同旁内角互补求出,然后求出 计算即可得解;
根据两直线平行,内错角相等可得 再根据三角形的一个外角等于与它不相邻的两个内角的和可得即可得解;
试题解析:
(1)∵CB∥OA,
∵平分
(2)这个比值不变,比值为1∶2.理由:
∵CB∥OA,
20.见解析
【解析】试题分析:(1)由平行线的性质求得∠BDC=∠1=35°,然后由邻补角的定义求得∠2的度数即可;
(2)由平行线的性质可知:∠A+∠ADC=180°,然后由∵∠A=∠C,再证得∠C+∠ADC=180°,从而可证得BC∥AD;
(3)由AE∥CF可证明∠BDF=∠DBE,由BC∥AD,可证明∠ADB=∠DBC,由角平分线的定义可知,∠ADB=∠BDF,从而可证明∠DBC=∠EBD.
试题解析:(1)∵AE∥CF,
∴∠BDC=∠1=35°,
又∵∠2+∠BDC=180°,
∴∠2=180°-∠BDC=180°-35°=145°;
(2)BC∥AD.
理由:∵AE∥CF,∴∠A+∠ADC=180°,
又∵∠A=∠C,∴∠C+∠ADC=180°,
∴BC∥AD.
(3)∵AE∥CF,∴∠BDF=∠DBE.
∵BC∥AD,∴∠ADB=∠DBC.
∵AD平分∠BDF,∴∠ADB=∠BDF,∴∠DBC=∠EBD.
∴BC平分∠DBE.
版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
