第2章 相交线与平行线单元检测提高卷
文档属性
| 名称 | 第2章 相交线与平行线单元检测提高卷 |  | |
| 格式 | docx | ||
| 文件大小 | 568.3KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-09 15:56:32 | ||
图片预览




文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
第2章相交线与平行线单元检测提高卷
姓名:__________班级:__________学号:__________
一、选择题
1.在同一平面内有三条直线a,b,c,如果a∥b,a与b的距离是2 cm,并且b上的点P到直线c的距离也是2 cm,那么b与c的位置关系是( )
A. 平行 B. 相交 C. 垂直 D. 不能确定
2.如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
A. 38° B. 42° C. 48° D. 58°
3.如图.已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP长不可能是( )
A. 2.5 B. 3 C. 4 D. 5
4.下列说法中,正确的是( )
A. 从直线外一点到这条直线的垂线叫点到直线的距离
B. 在同一平面内,过一点有且只有一条直线与已知直线平行
C. 在同一平面内,过一点有且只有一条直线与已知直线垂直
D. 不相交的两直线一定互相平行
5.如图,下列推理错误的是( )
A. ∵, B. ∵
C. D. ∵
6.如图,不能判断l1∥l2的条件是( )
A. ∠1=∠3 B. ∠2+∠4=180° C. ∠4=∠5 D. ∠2=∠3
7.如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
A. 90° B. 80° C. 70° D. 60°
8.一辆汽车在笔直的公路上行驶,两次拐弯后的方向与原来的方向相反,那么两次拐弯的角度可能是是( )
A. 第一次右拐60°,第二次左拐120°
B. 第一次左拐60°,第二次右拐60°
C. 第一次左拐60°,第二次左拐120°
D. 第一次右拐60°,第二次右拐60°
9.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90 ;④∠4+∠5=180 .其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
10.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
二、填空题
11.如图,直线AB、CD相交于点O,OM⊥AB于点O,若∠MOD=43°,则∠COB= 度.
12.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做的理由是________________.
13.如图,将一个等腰直角三角板按右图方式放置在一个矩形纸片上,其中∠α=20°,则∠β的度数为_________.
14.如图,点E在CD上,点F在BA上,G是AD延长线上一点.
(1 )若∠A=∠1,则可判断_______∥_______,因为________.
(2 )若∠1=∠_________,则可判断AG∥BC,因为_________.
(3 )若∠2+∠______=180°,则可判断CD∥AB,因为______
15.已知,如图,在△ABC中,BO和CO分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为________.
16.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变△ACD的位置(其中A点位置始终不变),使三角形ACD的一边与三角形AOB的某一边平行时,写出∠BAD的所有可能的值_____________
三、解答题
17.读语句画图:
()作直线.
()过点作直线的垂线,垂足.
()连接.
()画射线.
根据所作图填空:
①点与点的距离是图中线段__________的长度.
②点到直线的距离是线段__________的长度.
③若为直线上任一点,则与的关系是__________,其数学原理是__________.
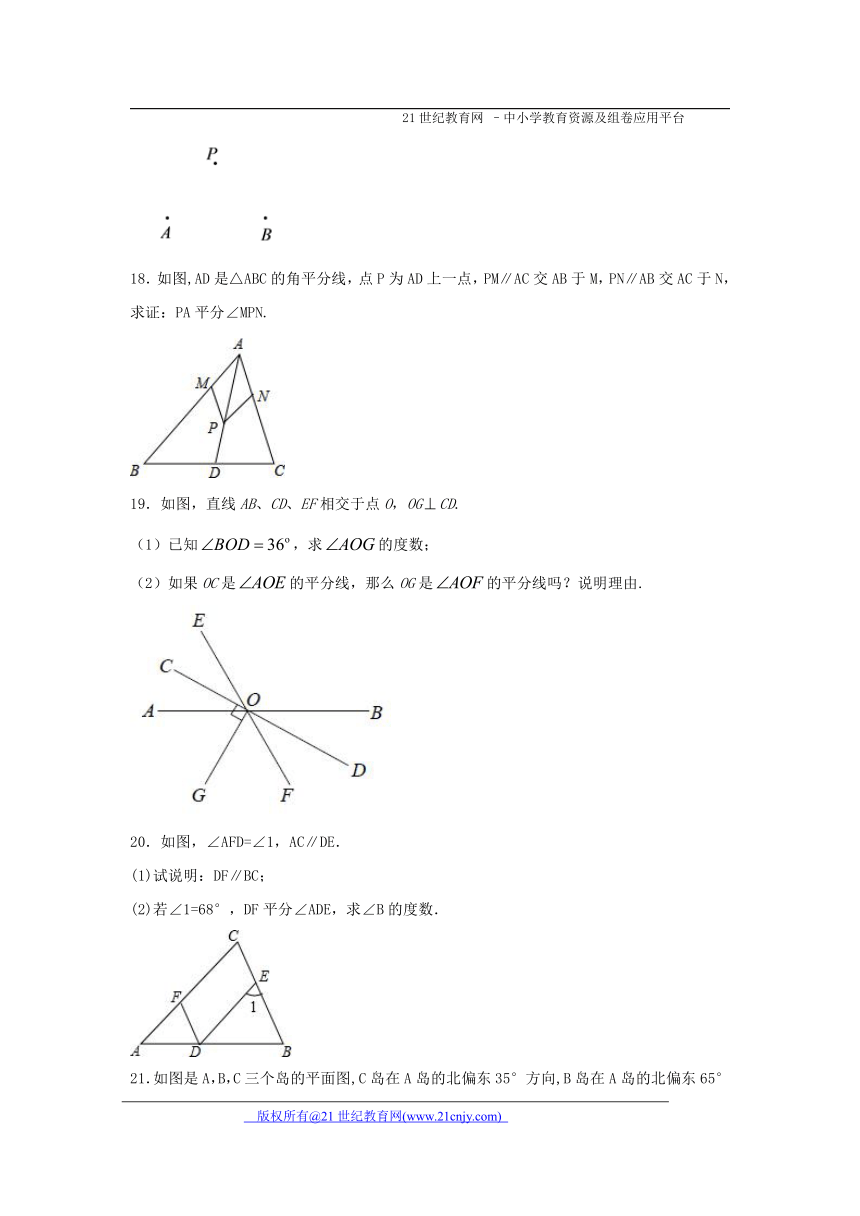
18.如图,AD是△ABC的角平分线,点P为AD上一点,PM∥AC交AB于M,PN∥AB交AC于N,求证:PA平分∠MPN.
19.如图,直线AB、CD、EF相交于点O,OGCD.
(1)已知,求的度数;
(2)如果OC是的平分线,那么OG是的平分线吗?说明理由.
20.如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
21.如图是A,B,C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.
(1)求C岛看A、B两岛的视角∠ACB的度数?
(2)聪明的刘凯同学发现解决第(1)问,可以不用“B岛在A岛的北偏东65°方向”这个条件,你能求吗?
22.如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
(1)求∠DAB的度数,并写出理由.
(2)求∠EAC的度数.
(3)计算∠BAC的度数.
(4)根据以上条件及结论,你还能得出其他结论吗?试写出一个.
23.有一天李小虎同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
24.(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
参考答案
1.D
【解析】A、B均有可能.,故选D.
2.C
【解析】试题分析:根据平行线的性质,可知∠2=∠3,然后根据垂直的定义,可知∠1+∠3=90°,再根据已知∠1=42°可求得∠3=48°.
故选:C.
点睛:此题主要考查了平行线的性质,先根据垂直的定义,得到直角,然后后利用两直线平行,内错角相等,可求出结果.
3.A
【解析】由垂线段最短可知AP≥AB=3,所以AP的长不可能是2.5;故选A.
4.C
【解析】试题分析:从直线外一点到这条直线的垂线的长度叫点到直线的距离,故A不正确;
在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故B不正确;
在同一平面内,过一点有且只有一条直线与已知直线垂直,故C正确;
在同一平面内,不相交的两直线一定互相平行,故D不正确.
故选:C.
5.D
【解析】A. ∵, ,正确; B. ∵,正确;C. ,正确; D. ∵,故D错误;故选D.
6.D
【解析】A. ∠1=∠3正确,内错角相等两直线平行;
B. ∠2+∠4=180°正确,同旁内角互补两直线平行;
C. ∠4=∠5正确,同位角相等两直线平行;
D. ∠2=∠3错误,它们不是同位角、内错角、同旁内角,故不能推断两直线平行。
故选D.
7.A
【解析】如图,过点C作CG∥AE,因为AE∥BF,所以AE∥CG∥BF,
所以∠ACG=∠CAE,∠BCG=∠CBF,
因为∠CAE=50°,∠CBF=40°,∴∠ACB=∠ACG+∠BCG=50°+40°=90°.
故选A.
点睛:本题主要考查了方向角和平行线的性质,在有关方向角的问题中,注意向北的方向是互相平行的,由此结合平行线的性质即可得到图形中的角的关系,解题的关键是要过点C作平行线.
8.C
【解析】试题分析:两次拐弯以后方向相反,那么2次同方向拐弯之和是180°.
故选:C.
9.D
【解析】根据平行线的性质,两直线平行,同位角相等,内错角相等,同旁内角互补,可知∠1=∠2,∠3=∠4,∠4+∠5=180°,再根据平角的定义和直角,可知∠2+∠4=90°.因此正确的个数为4.
故选:D.
10.D
【解析】试题解析:点有4种可能位置.
(1)如图,由∥ 可得
(2)如图,过 作平行线,则由∥可得
(3)如图,由∥可得
(4)如图,由∥可得
的度数可能为
故选:D.
11.133
【解析】∵OM⊥AB,
∴∠AOM=90°,
∵∠MOD=43°,
∴∠AOD=∠AOM+∠MOD=90°+43°=133°,
又因直线AB,CD相交于点O,∠COB与∠AOD是对顶角,
∴∠COB=∠AOD=133°.
12.垂线段最短
【解析】要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短,
故答案为:垂线段最短。
13.25°
【解析】
,
.
14. AB, DC, 同位角相等,两直线平行 C 内错角相等,两直线平行 EFB 同旁内角互补,两直线平行
【解析】(1)若∠A=∠1,则可判断AB∥CD,因为“同位角相等,两直线平行”;
(2)若∠1=∠C,则可判断AG∥BC,因为“内错角相等,两直线平行”;
(3)若∠2+∠EFB=180°,则可判断CD∥AB,因为“同旁内角互补,两直线平行”.
15.5
【解析】∵在△ABC中,BO和CO分别平分∠ABC和∠ACB, ∴∠DBO=∠OBC,∠ECO=∠OCB,
∵DE∥BC,
∴∠DOB=∠OBC=∠DBO,∠EOC=∠OCB=∠ECO,
∴DB=DO,OE=EC,
∵DE=DO+OE,
∴DE=BD+CE=5.
故答案为:5.
16.15°,30°,45°,75°,105°,135°,150°,165°
【解析】根据题意,
(1)当CD//OB时,如图所示:∠BAD=15°;
(2)当AD//OB时,如 图所示:∠BAD=45°;
(3)当CD//OA时,如图所示:∠BAD=105°;
(4)当AC//OB时,如图所示:∠BAD=135°;
(5)当AB//CD时,如图所示:∠BAD=150°;
(6)当CD//OB时,如图所示:∠BAD=165°;
(7)当CD//OA时,如图所示:∠BAD=75°;
(8)当CD//AB时,如图所示:∠BAD=30°;
故答案是:15°,30°,45°,75°,105°,135°,150°,165°。
17.画图见解析;①;②;③;点到直线间的距离垂线段最短.
【解析】试题分析:由直线、射线、线段的定义画图,再根据线段的长度及垂线线段的性质求解即可.
试题解析:①点A与点P的距离是图中线段AP的长度;
②点P到直线AB的距离是PM的长度;
③若Q为直线AB上任一点,则PQ与PM的关系是PQ≥PM.其数学原理是直线外一点到直线的距离中,垂线段最短.
故答案为:①;②;③;点到直线间的距离垂线段最短.
18.见解答
【解析】试题分析:先根据角平分线的定义得到∠BAD=∠CAD,由PM∥AC,PN∥AB,根据两直线平行,内错角相等得到∠APM=∠PAN,∠APN=∠PAM,然后经过等量代换即可得到∠APM=∠APN.
试题解析:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵PM∥AC,PN∥AB
∴∠APM=∠PAN,∠APN=∠PAM,
∴∠APM=∠APN,
∴PA平分∠MPN.
19.(1)54°;(2)详见解析.
【解析】试题分析:(1)根据对顶角的性质,可得∠AOC的度数,根据角的和差,可得答案;
(2)根据角平分线的性质,可得∠AOC与∠COE的关系,由垂直得到
,由平角的定义,得,由等量代换得,可得答案.
试题解析:(1)相交于点O,
(对顶角相等)
= 36o(已知)
= 36o
(已知)
(垂直的定义)
即
(2)OC平分
(角平分线定义)
(已证)
即
(平角定义)
(等式性质)
(等角的余角相等)
OG是AOF的角平分线(角平分线定义)
点睛:本题考查了角平分线的定义、对顶角的性质、邻补角的性质,掌握对顶角相等、垂直的定义是解题的关键.
20.(1)证明见解析;(2)68°.
【解析】试题分析:(1)由AC∥DE得∠1=∠C,而∠AFD=∠1,故∠AFD=∠C,故可得证;
(2)由(1)得∠EDF=68°,又DF平分∠ADE,所以∠EDA=68°,结合DF∥BC即可求出结果.
试题解析:(1)∵AC∥DE,
∴∠1=∠C,
∵∠AFD=∠1,
∴∠AFD=∠C,
∴DF∥BC;
(2)∵DF∥BC,
∴∠EDF=∠1=68°,
∵DF平分∠ADE,
∴∠EDA=∠EDF=68°,
∵∠ADE=∠1+∠B
∴∠B=∠ADE-∠1=68°+68°-68°=68°.
21.(1)∠ACB=75° (2)∠ACB=∠DAC+∠EBC
【解析】试题分析:(1)根据方位角的概念结合已知,可知∠DAC=35°,∠DAB=65°,∠CBE=40°,由AD∥BE,进而得到∠DAB+∠EBA=180°,由此不难求出∠CAB,∠ABC的度数,从而根据三角形内角和定理求出∠ACB的度数;
(2)可以不用“B岛在A岛的北偏东65°方向”这个条件,由∠DAB+∠EBA=180°,∠DAC=35°,∠CBE=40°,可直接求出∠CAB+∠CBA的度数,再结合三角形的内角和定理即可求出∠ACB的度数.
试题解析:(1)根据题意,可得∠DAC=35°,∠DAB=65°,∠CBE=40°.
则∠CAB=∠DAB-∠DAC=30°,
∵AD∥BE,
∴∠DAB+∠EBA=180°,
∴∠ABC=180°-∠DAB-∠CBE=180°-65°-40°=75°,
∴∠ACB=180°-∠CAB-∠CBA=180°-30°-75°=75°,
(2)可以不用“B岛在A岛的北偏东65°方向”这个条件.
∵AD∥BE,
∴∠DAB+∠EBA=180°,
∵∠DAC=35°,∠CBE=40°,
∴∠CAB+∠CBA=180°-∠DAC-∠CBE=105°,
∵∠CAB+∠CBA+∠ACB=180°,
∴∠ACB=180°-105°=75°.
22.(1)∠DAB的度数为45°,根据两直线平行,内错角相等得出.(2)∠EAC的度数是50°.(3)∠BAC=180°-∠DAB-∠EAC=180°-45°-50°=95°.(4)三角形ABC的内角和是180°
【解析】(1)由平行线的性质可得到∠DAB=∠B;(2)由平行线的性质可得到∠EAC=∠C;(3)由平角的定义可求得∠BAC,(4)结合(1)(2)(3)可得出结论.
解:(1)∵DE∥BC,
∴∠DAB=∠B=45°;
(2)∵DE∥BC,
∴∠EAC=∠C=50°,
(3)∵直线DE过点A,
∴∠DAE=180°,
∴∠DAB+∠EAC+∠BAC=180°,
∴∠BAC=180°-45°-50°=85°;
(4)∵DE∥BC,
∴∠B=∠DAB,∠C=∠EAC,
∵∠DAB+∠EAC+∠BAC=180°,
∴∠B+∠C+∠BAC=180°,
即三角形内角和为180°.
“点睛”本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,④a∥b,b∥c,a∥c.
23.(1)(1)图①:∠BED=∠B+∠D;图②:∠B+∠BED+∠D=360°;图③:∠BED=∠D-∠B;图④:∠BED=∠B-∠D;(2)证明见解析.
【解析】(1)根据两直线平行,内错角相等,即可解答;
(2)选择③,过点E作EF∥AB,根据两直线平行,内错角相等可得∠D=∠DEF,∠B=∠BEF,再根据∠BED=∠DEF-∠BEF即可证明.
解:(1)图①:∠BED=∠B+∠D;
图②:∠B+∠BED+∠D=360°;
图③:∠BED=∠D-∠B;
图④:∠BED=∠B-∠D.
(2)以图③为例:如图,过点E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠D=∠DEF,∠B=∠BEF.
∵∠BED=∠DEF-∠BEF,
∴∠BED=∠D-∠B.
点睛:本题主要考查平行线的性质.根据图形作出辅助线并灵活熟练运用平行线的性质是解题的关键.
24.(1)理由见解析
(2)AB∥CD.
(3)∠B+∠D+∠E=360°.
(4)∠B=∠D+∠E.
(5)∠E+∠G=∠B+∠F+∠D.
【解析】试题分析:已知AB∥CD,连接AB、CD的折线内折或外折,或改变E点位置、或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间,解题的关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形.
试题解析:(1)理由:过点E作EF∥AB,
∴∠B=∠BEF.
∵CD∥AB,∴CD∥EF.∴∠D=∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠BED.
(2)若∠B+∠D=∠E,由EF∥AB,得∠B=∠BEF,
∵∠E=∠BEF+∠DEF=∠B+∠D,
∴∠D=∠DEF,∴EF∥CD,
∴AB∥CD;
(3) 若将点E移至图2所示位置,过E作EF∥AB,
∴∠BEF+∠B=180°,
∵EF∥CD,
∴∠D+∠DEF=180°,
∠B+∠D+∠E=360°.
(4)∵AB∥CD,
∴∠B=∠BFD,
∵∠D+∠E=∠BFD,
∴∠D+∠E=∠B;
(5) 如图,作EM∥AB,FN∥AB,GP∥AB
∵AB∥CD,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D
∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D
∴∠1+∠2=∠E,5+∠6=∠G,∠3+∠4=∠F
∴E+∠G=∠B+∠F+∠D.
点睛:此题主要考查了平行线的性质,在解题时,通过添加辅助线,然后根据平行线的性质与判定可解题,此题添加辅助线是解题关键,只要添加合适辅助线即可正确求解.
版权所有@21世纪教育网(www.21cnjy.com)
第2章相交线与平行线单元检测提高卷
姓名:__________班级:__________学号:__________
一、选择题
1.在同一平面内有三条直线a,b,c,如果a∥b,a与b的距离是2 cm,并且b上的点P到直线c的距离也是2 cm,那么b与c的位置关系是( )
A. 平行 B. 相交 C. 垂直 D. 不能确定
2.如图,直线a∥b,直线c分别与a、b相交于A、B两点,AC⊥AB于点A,交直线b于点C.已知∠1=42°,则∠2的度数是( )
A. 38° B. 42° C. 48° D. 58°
3.如图.已知AB⊥BC,垂足为B,AB=3,点P是射线BC上的动点,则线段AP长不可能是( )
A. 2.5 B. 3 C. 4 D. 5
4.下列说法中,正确的是( )
A. 从直线外一点到这条直线的垂线叫点到直线的距离
B. 在同一平面内,过一点有且只有一条直线与已知直线平行
C. 在同一平面内,过一点有且只有一条直线与已知直线垂直
D. 不相交的两直线一定互相平行
5.如图,下列推理错误的是( )
A. ∵, B. ∵
C. D. ∵
6.如图,不能判断l1∥l2的条件是( )
A. ∠1=∠3 B. ∠2+∠4=180° C. ∠4=∠5 D. ∠2=∠3
7.如图,C岛在A岛的北偏东50°方向,C岛在B岛的北偏西40°方向,则从C岛看A,B两岛的视角∠ACB等于( )
A. 90° B. 80° C. 70° D. 60°
8.一辆汽车在笔直的公路上行驶,两次拐弯后的方向与原来的方向相反,那么两次拐弯的角度可能是是( )
A. 第一次右拐60°,第二次左拐120°
B. 第一次左拐60°,第二次右拐60°
C. 第一次左拐60°,第二次左拐120°
D. 第一次右拐60°,第二次右拐60°
9.将一直角三角板与两边平行的纸条如图所示放置,下列结论:①∠1=∠2;②∠3=∠4;③∠2+∠4=90 ;④∠4+∠5=180 .其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
10.如图,已知直线AB、CD被直线AC所截,AB∥CD,E是平面内任意一点(点E不在直线AB、CD、AC上),设∠BAE=α,∠DCE=β.下列各式:①α+β,②α﹣β,③β﹣α,④360°﹣α﹣β,∠AEC的度数可能是( )
A. ①②③ B. ①②④ C. ①③④ D. ①②③④
二、填空题
11.如图,直线AB、CD相交于点O,OM⊥AB于点O,若∠MOD=43°,则∠COB= 度.
12.如图,要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做的理由是________________.
13.如图,将一个等腰直角三角板按右图方式放置在一个矩形纸片上,其中∠α=20°,则∠β的度数为_________.
14.如图,点E在CD上,点F在BA上,G是AD延长线上一点.
(1 )若∠A=∠1,则可判断_______∥_______,因为________.
(2 )若∠1=∠_________,则可判断AG∥BC,因为_________.
(3 )若∠2+∠______=180°,则可判断CD∥AB,因为______
15.已知,如图,在△ABC中,BO和CO分别平分∠ABC和∠ACB,过O作DE∥BC,分别交AB、AC于点D、E,若BD+CE=5,则线段DE的长为________.
16.一副三角板按如图所示叠放在一起,其中点B、D重合,若固定三角形AOB,改变△ACD的位置(其中A点位置始终不变),使三角形ACD的一边与三角形AOB的某一边平行时,写出∠BAD的所有可能的值_____________
三、解答题
17.读语句画图:
()作直线.
()过点作直线的垂线,垂足.
()连接.
()画射线.
根据所作图填空:
①点与点的距离是图中线段__________的长度.
②点到直线的距离是线段__________的长度.
③若为直线上任一点,则与的关系是__________,其数学原理是__________.
18.如图,AD是△ABC的角平分线,点P为AD上一点,PM∥AC交AB于M,PN∥AB交AC于N,求证:PA平分∠MPN.
19.如图,直线AB、CD、EF相交于点O,OGCD.
(1)已知,求的度数;
(2)如果OC是的平分线,那么OG是的平分线吗?说明理由.
20.如图,∠AFD=∠1,AC∥DE.
(1)试说明:DF∥BC;
(2)若∠1=68°,DF平分∠ADE,求∠B的度数.
21.如图是A,B,C三个岛的平面图,C岛在A岛的北偏东35°方向,B岛在A岛的北偏东65°方向,C岛在B岛的北偏西40°方向.
(1)求C岛看A、B两岛的视角∠ACB的度数?
(2)聪明的刘凯同学发现解决第(1)问,可以不用“B岛在A岛的北偏东65°方向”这个条件,你能求吗?
22.如图,直线DE经过点A,DE∥BC,∠B=45°,∠C=50°,
(1)求∠DAB的度数,并写出理由.
(2)求∠EAC的度数.
(3)计算∠BAC的度数.
(4)根据以上条件及结论,你还能得出其他结论吗?试写出一个.
23.有一天李小虎同学用“几何画板”画图,他先画了两条平行线AB,CD,然后在平行线间画了一点E,连接BE,DE后(如图①),他用鼠标左键点住点E,拖动后,分别得到如图②,③,④等图形,这时他突然一想,∠B,∠D与∠BED之间的度数有没有某种联系呢?接着小虎同学通过利用“几何画板”的“度量角度”和“计算”功能,找到了这三个角之间的关系.
(1)你能探究出图①到图④各图中的∠B,∠D与∠BED之间的关系吗?
(2)请从所得的四个关系中,选一个说明它成立的理由.
24.(1)如图1,若AB∥CD,则∠B+∠D=∠E,你能说明理由吗?
(2)反之,若∠B+∠D=∠E,直线AB与CD有什么位置关系?
(3)若将点E移至图2的位置,此时∠B,∠D,∠E之间有什么关系?
(4)若将点E移至图3的位置,此时∠B,∠D,∠E之间的关系又如何?
(5)在图4中,AB∥CD,∠E+∠G与∠B+∠F+∠D之间有何关系?
参考答案
1.D
【解析】A、B均有可能.,故选D.
2.C
【解析】试题分析:根据平行线的性质,可知∠2=∠3,然后根据垂直的定义,可知∠1+∠3=90°,再根据已知∠1=42°可求得∠3=48°.
故选:C.
点睛:此题主要考查了平行线的性质,先根据垂直的定义,得到直角,然后后利用两直线平行,内错角相等,可求出结果.
3.A
【解析】由垂线段最短可知AP≥AB=3,所以AP的长不可能是2.5;故选A.
4.C
【解析】试题分析:从直线外一点到这条直线的垂线的长度叫点到直线的距离,故A不正确;
在同一平面内,过直线外一点有且只有一条直线与已知直线平行,故B不正确;
在同一平面内,过一点有且只有一条直线与已知直线垂直,故C正确;
在同一平面内,不相交的两直线一定互相平行,故D不正确.
故选:C.
5.D
【解析】A. ∵, ,正确; B. ∵,正确;C. ,正确; D. ∵,故D错误;故选D.
6.D
【解析】A. ∠1=∠3正确,内错角相等两直线平行;
B. ∠2+∠4=180°正确,同旁内角互补两直线平行;
C. ∠4=∠5正确,同位角相等两直线平行;
D. ∠2=∠3错误,它们不是同位角、内错角、同旁内角,故不能推断两直线平行。
故选D.
7.A
【解析】如图,过点C作CG∥AE,因为AE∥BF,所以AE∥CG∥BF,
所以∠ACG=∠CAE,∠BCG=∠CBF,
因为∠CAE=50°,∠CBF=40°,∴∠ACB=∠ACG+∠BCG=50°+40°=90°.
故选A.
点睛:本题主要考查了方向角和平行线的性质,在有关方向角的问题中,注意向北的方向是互相平行的,由此结合平行线的性质即可得到图形中的角的关系,解题的关键是要过点C作平行线.
8.C
【解析】试题分析:两次拐弯以后方向相反,那么2次同方向拐弯之和是180°.
故选:C.
9.D
【解析】根据平行线的性质,两直线平行,同位角相等,内错角相等,同旁内角互补,可知∠1=∠2,∠3=∠4,∠4+∠5=180°,再根据平角的定义和直角,可知∠2+∠4=90°.因此正确的个数为4.
故选:D.
10.D
【解析】试题解析:点有4种可能位置.
(1)如图,由∥ 可得
(2)如图,过 作平行线,则由∥可得
(3)如图,由∥可得
(4)如图,由∥可得
的度数可能为
故选:D.
11.133
【解析】∵OM⊥AB,
∴∠AOM=90°,
∵∠MOD=43°,
∴∠AOD=∠AOM+∠MOD=90°+43°=133°,
又因直线AB,CD相交于点O,∠COB与∠AOD是对顶角,
∴∠COB=∠AOD=133°.
12.垂线段最短
【解析】要把河中的水引到水池A中,应在河岸B处(AB⊥CD)开始挖渠才能使水渠的长度最短,这样做依据的几何学原理是垂线段最短,
故答案为:垂线段最短。
13.25°
【解析】
,
.
14. AB, DC, 同位角相等,两直线平行 C 内错角相等,两直线平行 EFB 同旁内角互补,两直线平行
【解析】(1)若∠A=∠1,则可判断AB∥CD,因为“同位角相等,两直线平行”;
(2)若∠1=∠C,则可判断AG∥BC,因为“内错角相等,两直线平行”;
(3)若∠2+∠EFB=180°,则可判断CD∥AB,因为“同旁内角互补,两直线平行”.
15.5
【解析】∵在△ABC中,BO和CO分别平分∠ABC和∠ACB, ∴∠DBO=∠OBC,∠ECO=∠OCB,
∵DE∥BC,
∴∠DOB=∠OBC=∠DBO,∠EOC=∠OCB=∠ECO,
∴DB=DO,OE=EC,
∵DE=DO+OE,
∴DE=BD+CE=5.
故答案为:5.
16.15°,30°,45°,75°,105°,135°,150°,165°
【解析】根据题意,
(1)当CD//OB时,如图所示:∠BAD=15°;
(2)当AD//OB时,如 图所示:∠BAD=45°;
(3)当CD//OA时,如图所示:∠BAD=105°;
(4)当AC//OB时,如图所示:∠BAD=135°;
(5)当AB//CD时,如图所示:∠BAD=150°;
(6)当CD//OB时,如图所示:∠BAD=165°;
(7)当CD//OA时,如图所示:∠BAD=75°;
(8)当CD//AB时,如图所示:∠BAD=30°;
故答案是:15°,30°,45°,75°,105°,135°,150°,165°。
17.画图见解析;①;②;③;点到直线间的距离垂线段最短.
【解析】试题分析:由直线、射线、线段的定义画图,再根据线段的长度及垂线线段的性质求解即可.
试题解析:①点A与点P的距离是图中线段AP的长度;
②点P到直线AB的距离是PM的长度;
③若Q为直线AB上任一点,则PQ与PM的关系是PQ≥PM.其数学原理是直线外一点到直线的距离中,垂线段最短.
故答案为:①;②;③;点到直线间的距离垂线段最短.
18.见解答
【解析】试题分析:先根据角平分线的定义得到∠BAD=∠CAD,由PM∥AC,PN∥AB,根据两直线平行,内错角相等得到∠APM=∠PAN,∠APN=∠PAM,然后经过等量代换即可得到∠APM=∠APN.
试题解析:∵AD是△ABC的角平分线,
∴∠BAD=∠CAD,
∵PM∥AC,PN∥AB
∴∠APM=∠PAN,∠APN=∠PAM,
∴∠APM=∠APN,
∴PA平分∠MPN.
19.(1)54°;(2)详见解析.
【解析】试题分析:(1)根据对顶角的性质,可得∠AOC的度数,根据角的和差,可得答案;
(2)根据角平分线的性质,可得∠AOC与∠COE的关系,由垂直得到
,由平角的定义,得,由等量代换得,可得答案.
试题解析:(1)相交于点O,
(对顶角相等)
= 36o(已知)
= 36o
(已知)
(垂直的定义)
即
(2)OC平分
(角平分线定义)
(已证)
即
(平角定义)
(等式性质)
(等角的余角相等)
OG是AOF的角平分线(角平分线定义)
点睛:本题考查了角平分线的定义、对顶角的性质、邻补角的性质,掌握对顶角相等、垂直的定义是解题的关键.
20.(1)证明见解析;(2)68°.
【解析】试题分析:(1)由AC∥DE得∠1=∠C,而∠AFD=∠1,故∠AFD=∠C,故可得证;
(2)由(1)得∠EDF=68°,又DF平分∠ADE,所以∠EDA=68°,结合DF∥BC即可求出结果.
试题解析:(1)∵AC∥DE,
∴∠1=∠C,
∵∠AFD=∠1,
∴∠AFD=∠C,
∴DF∥BC;
(2)∵DF∥BC,
∴∠EDF=∠1=68°,
∵DF平分∠ADE,
∴∠EDA=∠EDF=68°,
∵∠ADE=∠1+∠B
∴∠B=∠ADE-∠1=68°+68°-68°=68°.
21.(1)∠ACB=75° (2)∠ACB=∠DAC+∠EBC
【解析】试题分析:(1)根据方位角的概念结合已知,可知∠DAC=35°,∠DAB=65°,∠CBE=40°,由AD∥BE,进而得到∠DAB+∠EBA=180°,由此不难求出∠CAB,∠ABC的度数,从而根据三角形内角和定理求出∠ACB的度数;
(2)可以不用“B岛在A岛的北偏东65°方向”这个条件,由∠DAB+∠EBA=180°,∠DAC=35°,∠CBE=40°,可直接求出∠CAB+∠CBA的度数,再结合三角形的内角和定理即可求出∠ACB的度数.
试题解析:(1)根据题意,可得∠DAC=35°,∠DAB=65°,∠CBE=40°.
则∠CAB=∠DAB-∠DAC=30°,
∵AD∥BE,
∴∠DAB+∠EBA=180°,
∴∠ABC=180°-∠DAB-∠CBE=180°-65°-40°=75°,
∴∠ACB=180°-∠CAB-∠CBA=180°-30°-75°=75°,
(2)可以不用“B岛在A岛的北偏东65°方向”这个条件.
∵AD∥BE,
∴∠DAB+∠EBA=180°,
∵∠DAC=35°,∠CBE=40°,
∴∠CAB+∠CBA=180°-∠DAC-∠CBE=105°,
∵∠CAB+∠CBA+∠ACB=180°,
∴∠ACB=180°-105°=75°.
22.(1)∠DAB的度数为45°,根据两直线平行,内错角相等得出.(2)∠EAC的度数是50°.(3)∠BAC=180°-∠DAB-∠EAC=180°-45°-50°=95°.(4)三角形ABC的内角和是180°
【解析】(1)由平行线的性质可得到∠DAB=∠B;(2)由平行线的性质可得到∠EAC=∠C;(3)由平角的定义可求得∠BAC,(4)结合(1)(2)(3)可得出结论.
解:(1)∵DE∥BC,
∴∠DAB=∠B=45°;
(2)∵DE∥BC,
∴∠EAC=∠C=50°,
(3)∵直线DE过点A,
∴∠DAE=180°,
∴∠DAB+∠EAC+∠BAC=180°,
∴∠BAC=180°-45°-50°=85°;
(4)∵DE∥BC,
∴∠B=∠DAB,∠C=∠EAC,
∵∠DAB+∠EAC+∠BAC=180°,
∴∠B+∠C+∠BAC=180°,
即三角形内角和为180°.
“点睛”本题主要考查平行线的性质,掌握平行线的性质和判定是解题的关键,即①两直线平行,同位角相等,②两直线平行,内错角相等,③两直线平行,同旁内角互补,④a∥b,b∥c,a∥c.
23.(1)(1)图①:∠BED=∠B+∠D;图②:∠B+∠BED+∠D=360°;图③:∠BED=∠D-∠B;图④:∠BED=∠B-∠D;(2)证明见解析.
【解析】(1)根据两直线平行,内错角相等,即可解答;
(2)选择③,过点E作EF∥AB,根据两直线平行,内错角相等可得∠D=∠DEF,∠B=∠BEF,再根据∠BED=∠DEF-∠BEF即可证明.
解:(1)图①:∠BED=∠B+∠D;
图②:∠B+∠BED+∠D=360°;
图③:∠BED=∠D-∠B;
图④:∠BED=∠B-∠D.
(2)以图③为例:如图,过点E作EF∥AB,
∵AB∥CD,
∴EF∥CD,
∴∠D=∠DEF,∠B=∠BEF.
∵∠BED=∠DEF-∠BEF,
∴∠BED=∠D-∠B.
点睛:本题主要考查平行线的性质.根据图形作出辅助线并灵活熟练运用平行线的性质是解题的关键.
24.(1)理由见解析
(2)AB∥CD.
(3)∠B+∠D+∠E=360°.
(4)∠B=∠D+∠E.
(5)∠E+∠G=∠B+∠F+∠D.
【解析】试题分析:已知AB∥CD,连接AB、CD的折线内折或外折,或改变E点位置、或增加折线的条数,通过适当地改变其中的一个条件,就能得出新的结论,给我们创造性的思考留下了极大的空间,解题的关键是过E点作AB(或CD)的平行线,把复杂的图形化归为基本图形.
试题解析:(1)理由:过点E作EF∥AB,
∴∠B=∠BEF.
∵CD∥AB,∴CD∥EF.∴∠D=∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠BED.
(2)若∠B+∠D=∠E,由EF∥AB,得∠B=∠BEF,
∵∠E=∠BEF+∠DEF=∠B+∠D,
∴∠D=∠DEF,∴EF∥CD,
∴AB∥CD;
(3) 若将点E移至图2所示位置,过E作EF∥AB,
∴∠BEF+∠B=180°,
∵EF∥CD,
∴∠D+∠DEF=180°,
∠B+∠D+∠E=360°.
(4)∵AB∥CD,
∴∠B=∠BFD,
∵∠D+∠E=∠BFD,
∴∠D+∠E=∠B;
(5) 如图,作EM∥AB,FN∥AB,GP∥AB
∵AB∥CD,
∴∠B=∠1,∠2=∠3,∠4=∠5,∠6=∠D
∴∠1+∠2+∠5+∠6=∠B+∠3+∠4+∠D
∴∠1+∠2=∠E,5+∠6=∠G,∠3+∠4=∠F
∴E+∠G=∠B+∠F+∠D.
点睛:此题主要考查了平行线的性质,在解题时,通过添加辅助线,然后根据平行线的性质与判定可解题,此题添加辅助线是解题关键,只要添加合适辅助线即可正确求解.
版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 整式的乘除
- 1 同底数幂的乘法
- 2 幂的乘方与积的乘方
- 3 同底数幂的除法
- 4 整式的乘法
- 5 平方差公式
- 6 完全平方公式
- 7 整式的除法
- 第二章 相交线与平行线
- 1 两条直线的位置关系
- 2 探索直线平行的条件
- 3 平行线的性质
- 4 用尺规作角
- 第三章 变量之间的关系
- 1 用表格表示的变量间关系
- 2 用关系式表示的变量间关系
- 3 用图象表示的变量间关系
- 第四章 三角形
- 1 认识三角形
- 2 图形的全等
- 3 探索三角形全等的条件
- 4 用尺规作三角形
- 5 利用三角形全等测距离
- 第五章 生活中的轴对称
- 1 轴对称现象
- 2 探索轴对称的性质
- 3 简单的轴对称图形
- 4 利用轴对称进行设计
- 第六章 概率初步
- 1 感受可能性
- 2 频率的稳定性
- 3 等可能事件的概率
