第09讲:必修3第二章《统计》单元检测题-高中数学单元检测题 Word版含解析
文档属性
| 名称 | 第09讲:必修3第二章《统计》单元检测题-高中数学单元检测题 Word版含解析 |

|
|
| 格式 | zip | ||
| 文件大小 | 540.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-08 00:00:00 | ||
图片预览



文档简介
必修3第二章《统计》单元检测题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.某班的60名同学已编号1,2,3,…,60,为了解该班同学的作业情况,老师收取了号码能被5整除的12名同学的作业本,这里运用的抽样方法是( )
A.简单随机抽样 B.系统抽样
C.分层抽样 D.抽签法
2.某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为 的学生.
A .37 B .36 C .35 D . 38
3.已知变量x和y满足关系y=0.1x-10,变量z与y负相关,则下列结论中正确的是
( )
A.x与y负相关,x与z负相关
B.x与y正相关,x与z正相关
C.x与y正相关,x与z负相关
D.x与y负相关,x与z正相关
4.某市A,B,C三个区共有高中学生20000人,其中A区高中学生7 000人,现采用分层抽样的方法从这三个区所有高中学生中抽取一个容量为600的样本进行“学习兴趣”调查,则在A区应抽取( )
A.200人 B.205人
C.210人 D.215人
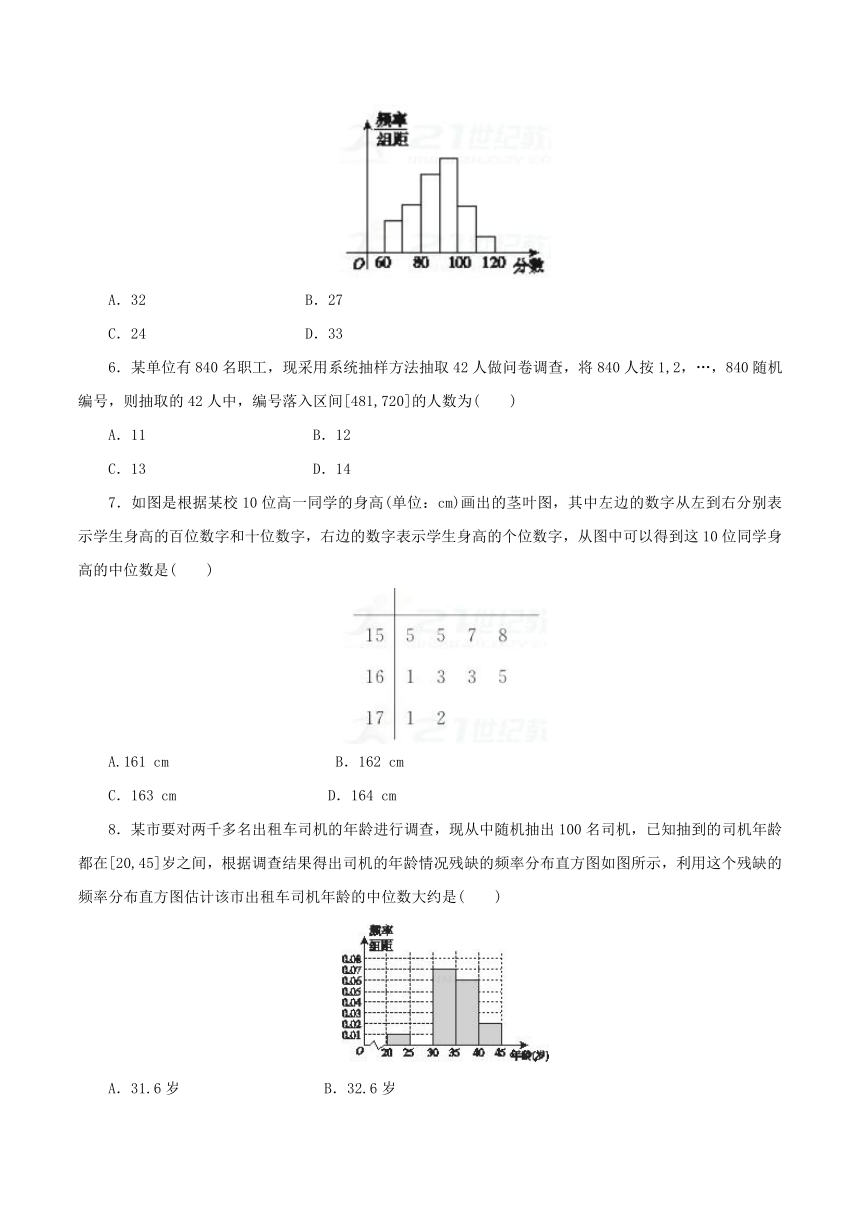
5.为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图所示.已知从左到右各长方形高的比为2∶3∶5∶6∶3∶1,则该班学生数学成绩在[80,100)之间的学生人数是( )
A.32 B.27
C.24 D.33
6.某单位有840名职工,现采用系统抽样方法抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为( )
A.11 B.12
C.13 D.14
7.如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中位数是( )
A.161 cm B.162 cm
C.163 cm D.164 cm
8.某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45]岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
A.31.6岁 B.32.6岁
C.33.6岁 D.36.6岁
9.在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积和的,且样本容量为160,则中间一组的频数为( )
A.32 B.0.2
C.40 D.0.25
10.对一个样本容量为100的数据分组,各组的频数如下:
区间
[17,19)
[19,21)
[21,23)
[23,25)
[25,27)
[27,29)
[29,31)
[31,33]
频数
1
1
3
3
18
16
28
30
估计小于29的数据大约占总体的( )
A.42% B.58%
C.40% D.16%
11.某企业三月中旬生产A,B,C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的统计表格.由于不小心,表格中A,C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10件,根据以上信息,可得C产品的数量是( )
产品类别
A
B
C
产品数量(件)
1 300
样本容量(件)
130
A.900件 B.800件
C.90件 D.80件
12.已知x,y的取值如下表所示:
x
2
3
4
y
6
4
5
如果y与x线性相关,且线性回归方程为=x+,则=( )
A. B.-
C. D.1
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.某年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,则此样本中男生人数为________.
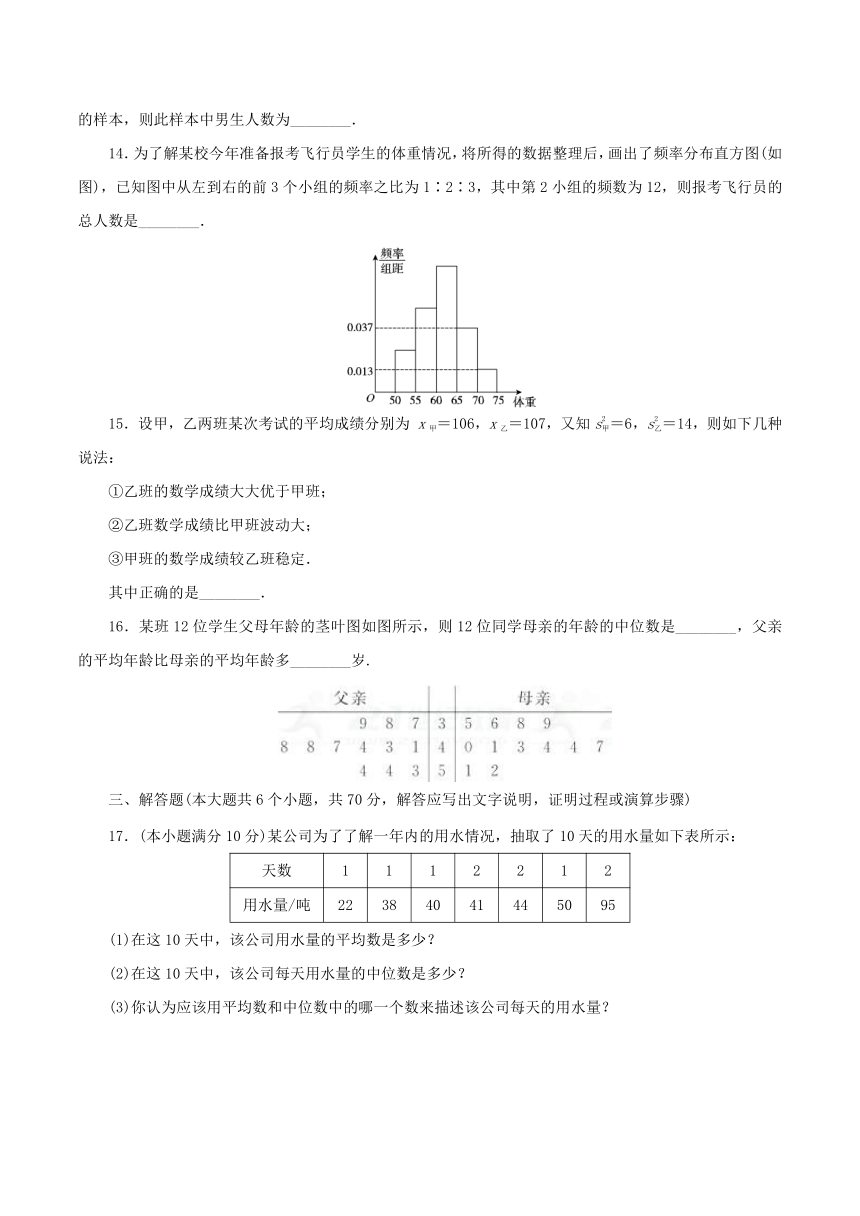
14.为了解某校今年准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1∶2∶3,其中第2小组的频数为12,则报考飞行员的总人数是________.
15.设甲,乙两班某次考试的平均成绩分别为 x甲=106,x乙=107,又知s=6,s=14,则如下几种说法:
①乙班的数学成绩大大优于甲班;
②乙班数学成绩比甲班波动大;
③甲班的数学成绩较乙班稳定.
其中正确的是________.
16.某班12位学生父母年龄的茎叶图如图所示,则12位同学母亲的年龄的中位数是________,父亲的平均年龄比母亲的平均年龄多________岁.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数
1
1
1
2
2
1
2
用水量/吨
22
38
40
41
44
50
95
(1)在这10天中,该公司用水量的平均数是多少?
(2)在这10天中,该公司每天用水量的中位数是多少?
(3)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
18.(本小题满分12分)农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在右面给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
19.(本小题满分12分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加较合适?请说明理由.
20.(本小题满分12分)某个服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这些服装件数x之间有如下一组数据:
x
3
4
5
6
7
8
9
y
66
69
73
81
89
90
91
已知=280,iyi=3 487,
(1)求,;
(2)求纯利y与每天销售件数x之间的回归直线方程;
(3)每天多销售1件,纯利y增加多少元?
21.(本小题满分12分)某某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
分组
频数
频率
一组
0≤t<5
0
0
二组
5≤t<10
10
三组
10≤t<15
10
0.10
四组
15≤t<20
五组
20≤t<25
30
0.30
合计
100
1.00
(1)这次抽样的样本容量是多少?
(2)在表中填写缺失的数据并补全频率分布直方图.
(3)旅客购票用时的平均数可能落在哪一个小组?
(4)若每增加一个购票窗口可使平均购票用时缩短5 min,要使平均购票用时不超过10 min,那么你估计最少要增加几个窗口?
22.(本小题满分12分)某地统计局就该地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)).
(1)求居民月收入在[3 000,3 500)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中用分层抽样方法抽出100人作进一步分析,则月收入在[2 500,3 000)的这段应抽多少人?
必修3第二章《统计》单元检测题参考答案
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
C
C
D
B
B
C
A
A
B
B
【第1题解析】抽出的号码是5,10,15,…,60,符合系统抽样的特点:“等距抽样”.故选B.
【第2题解析】根据题意,由系统抽样的方法规则,知:若在第三组中抽得号码为12的学生,则在第八组中抽得号码为的学生.故选A.
【第6题解析】840÷42=20,把1,2,…,840分成42段,不妨设第1段抽取的号码为l,则第k段抽取的号码为l+(k-1)·20,1≤l≤20,1≤k≤42.令481≤l+(k-1)·20≤720,得25+≤k≤37-.由1≤l≤20,则25≤k≤36.满足条件的k共有12个.故选B.
【第7题解析】由中位数的定义得选B,故选B.
【第8题解析】由频率分布直方图可知[25,30)的频率应为0.2,又[20,25)的频率为0.05,[30,35)的频率为0.35,计算可得中位数约为33.6,故选C.
【第9题解析】设中间长方形的面积等于S,则S=(1-S),S=,设中间一组的频数为x,则=,得x=32. 故选A.
【第10题解析】样本中小于29的数据频数为1+1+3+3+18+16=42.,所以小于29的数据大约占总体的×100%=42%. 故选A.
【第11题解析】设A,C产品数量分别为x件、y件,则由题意可得:所以所以故选B.
【第12题解析】因为=3,=5,又回归直线过点(,),所以5=3+,
所以=-. 故选B .
填空题答案
第13题
160
第14题
48
第15题
②③
第16题
42 3
【第15题解析】①平均成绩x甲=106,x乙=107,平均水平相近,不存在说乙班的数学成绩大大优于甲班.①错.②s=6,s=14,s<s,乙班数学成绩比甲班波动大. ②对;③s<s,甲班的数学成绩较乙班稳定,③对. 故填②③.
【第16题解析】由=42,得中位数是42. 母亲平均年龄=42.5,父亲平均年龄为45.5,因而父亲平均年龄比母亲平均年龄多3岁.故填42 3 .
【第17题答案】(1)51;(2)42.5 ;(3)中位数描述每天的用水量更合适.
【第17题解析】 (1)=(22+38+40+2×41+2×44+50+2×95)=51(吨).
(2)中位数为=42.5(吨).
(3)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下,故用中位数描述每天的用水量更合适.
【第18题答案】(1)茎叶图见解析;(2)乙种麦苗平均株高较高,甲种麦苗长得较为整齐.
【第18题解析】(1)茎叶图如图所示:
(2)甲==12,
乙==13,
s≈13.67,s≈16.67.
因为甲<乙,所以乙种麦苗平均株高较高,又因为s<s,所以甲种麦苗长得较为整齐.
s=[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5,
s=[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41.
∵甲=乙,s<s,
∴甲的成绩较稳定,派甲参赛比较合适.
【第20题答案】(1)6,79.86;(2)=51.36+4.75x,(3)每天多销售1件,纯利平均增加4.75元.
【第20题解析】(1)=(3+4+5+…+9)=6,
=(66+69+…+91)≈79.86.
(2)设回归直线方程为=+x,
则==≈4.75.
=- ≈79.86-4.75×6=51.36.
∴所求的回归直线方程为=51.36+4.75x.
(2)
分组
频数
频率
一组
0≤t<5
0
0
二组
5≤t<10
10
0.10
三组
10≤t<15
10
0.10
四组
15≤t<20
50
0.50
五组
20≤t<25
30
0.30
合计
100
1.00
(3)设旅客平均购票时间为s min,则有
≤
s<,
解得15≤s<20,
故旅客购票用时平均数可能落在第四小组.
(4)设需增加x个窗口,则20-5x≤10,解得x≥2,故至少需要增加2个窗口.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.某班的60名同学已编号1,2,3,…,60,为了解该班同学的作业情况,老师收取了号码能被5整除的12名同学的作业本,这里运用的抽样方法是( )
A.简单随机抽样 B.系统抽样
C.分层抽样 D.抽签法
2.某班级有50名学生,现要采取系统抽样的方法在这50名学生中抽出10名学生,将这50名学生随机编号1~50号,并分组,第一组1~5号,第二组6~10号,…,第十组46~50号,若在第三组中抽得号码为12的学生,则在第八组中抽得号码为 的学生.
A .37 B .36 C .35 D . 38
3.已知变量x和y满足关系y=0.1x-10,变量z与y负相关,则下列结论中正确的是
( )
A.x与y负相关,x与z负相关
B.x与y正相关,x与z正相关
C.x与y正相关,x与z负相关
D.x与y负相关,x与z正相关
4.某市A,B,C三个区共有高中学生20000人,其中A区高中学生7 000人,现采用分层抽样的方法从这三个区所有高中学生中抽取一个容量为600的样本进行“学习兴趣”调查,则在A区应抽取( )
A.200人 B.205人
C.210人 D.215人
5.为了了解高三学生的数学成绩,抽取了某班60名学生,将所得数据整理后,画出其频率分布直方图,如图所示.已知从左到右各长方形高的比为2∶3∶5∶6∶3∶1,则该班学生数学成绩在[80,100)之间的学生人数是( )
A.32 B.27
C.24 D.33
6.某单位有840名职工,现采用系统抽样方法抽取42人做问卷调查,将840人按1,2,…,840随机编号,则抽取的42人中,编号落入区间[481,720]的人数为( )
A.11 B.12
C.13 D.14
7.如图是根据某校10位高一同学的身高(单位:cm)画出的茎叶图,其中左边的数字从左到右分别表示学生身高的百位数字和十位数字,右边的数字表示学生身高的个位数字,从图中可以得到这10位同学身高的中位数是( )
A.161 cm B.162 cm
C.163 cm D.164 cm
8.某市要对两千多名出租车司机的年龄进行调查,现从中随机抽出100名司机,已知抽到的司机年龄都在[20,45]岁之间,根据调查结果得出司机的年龄情况残缺的频率分布直方图如图所示,利用这个残缺的频率分布直方图估计该市出租车司机年龄的中位数大约是( )
A.31.6岁 B.32.6岁
C.33.6岁 D.36.6岁
9.在样本的频率分布直方图中,共有11个小长方形,若中间一个小长方形的面积等于其他10个小长方形的面积和的,且样本容量为160,则中间一组的频数为( )
A.32 B.0.2
C.40 D.0.25
10.对一个样本容量为100的数据分组,各组的频数如下:
区间
[17,19)
[19,21)
[21,23)
[23,25)
[25,27)
[27,29)
[29,31)
[31,33]
频数
1
1
3
3
18
16
28
30
估计小于29的数据大约占总体的( )
A.42% B.58%
C.40% D.16%
11.某企业三月中旬生产A,B,C三种产品共3 000件,根据分层抽样的结果,企业统计员制作了如下的统计表格.由于不小心,表格中A,C产品的有关数据已被污染看不清楚,统计员记得A产品的样本容量比C产品的样本容量多10件,根据以上信息,可得C产品的数量是( )
产品类别
A
B
C
产品数量(件)
1 300
样本容量(件)
130
A.900件 B.800件
C.90件 D.80件
12.已知x,y的取值如下表所示:
x
2
3
4
y
6
4
5
如果y与x线性相关,且线性回归方程为=x+,则=( )
A. B.-
C. D.1
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.某年级有男生560人,女生420人,用分层抽样的方法从该年级全体学生中抽取一个容量为280的样本,则此样本中男生人数为________.
14.为了解某校今年准备报考飞行员学生的体重情况,将所得的数据整理后,画出了频率分布直方图(如图),已知图中从左到右的前3个小组的频率之比为1∶2∶3,其中第2小组的频数为12,则报考飞行员的总人数是________.
15.设甲,乙两班某次考试的平均成绩分别为 x甲=106,x乙=107,又知s=6,s=14,则如下几种说法:
①乙班的数学成绩大大优于甲班;
②乙班数学成绩比甲班波动大;
③甲班的数学成绩较乙班稳定.
其中正确的是________.
16.某班12位学生父母年龄的茎叶图如图所示,则12位同学母亲的年龄的中位数是________,父亲的平均年龄比母亲的平均年龄多________岁.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)某公司为了了解一年内的用水情况,抽取了10天的用水量如下表所示:
天数
1
1
1
2
2
1
2
用水量/吨
22
38
40
41
44
50
95
(1)在这10天中,该公司用水量的平均数是多少?
(2)在这10天中,该公司每天用水量的中位数是多少?
(3)你认为应该用平均数和中位数中的哪一个数来描述该公司每天的用水量?
18.(本小题满分12分)农科院的专家为了了解新培育的甲、乙两种麦苗的长势情况,从甲、乙两种麦苗的试验田中各抽取6株麦苗测量麦苗的株高,数据如下:(单位:cm)
甲:9,10,11,12,10,20
乙:8,14,13,10,12,21.
(1)在右面给出的方框内绘出所抽取的甲、乙两种麦苗株高的茎叶图;
(2)分别计算所抽取的甲、乙两种麦苗株高的平均数与方差,并由此判断甲、乙两种麦苗的长势情况.
19.(本小题满分12分)甲、乙两位学生参加数学竞赛培训,现分别从他们在培训期间参加的若干次预赛成绩中随机抽取8次,记录如下:
甲:82 81 79 78 95 88 93 84
乙:92 95 80 75 83 80 90 85
(1)用茎叶图表示这两组数据;
(2)现要从中选派一人参加数学竞赛,你认为选派哪位学生参加较合适?请说明理由.
20.(本小题满分12分)某个服装店经营某种服装,在某周内获纯利y(元)与该周每天销售这些服装件数x之间有如下一组数据:
x
3
4
5
6
7
8
9
y
66
69
73
81
89
90
91
已知=280,iyi=3 487,
(1)求,;
(2)求纯利y与每天销售件数x之间的回归直线方程;
(3)每天多销售1件,纯利y增加多少元?
21.(本小题满分12分)某某车站在春运期间为了改进服务,随机抽样调查了100名旅客从开始在购票窗口排队到购到车票所用的时间t(以下简称购票用时,单位:min).下面是这次抽样的频率分布表和频率分布直方图,解答下列问题:
分组
频数
频率
一组
0≤t<5
0
0
二组
5≤t<10
10
三组
10≤t<15
10
0.10
四组
15≤t<20
五组
20≤t<25
30
0.30
合计
100
1.00
(1)这次抽样的样本容量是多少?
(2)在表中填写缺失的数据并补全频率分布直方图.
(3)旅客购票用时的平均数可能落在哪一个小组?
(4)若每增加一个购票窗口可使平均购票用时缩短5 min,要使平均购票用时不超过10 min,那么你估计最少要增加几个窗口?
22.(本小题满分12分)某地统计局就该地居民的月收入调查了10 000人,并根据所得数据画了样本的频率分布直方图(每个分组包括左端点,不包括右端点,如第一组表示收入在[1 000,1 500)).
(1)求居民月收入在[3 000,3 500)的频率;
(2)根据频率分布直方图算出样本数据的中位数;
(3)为了分析居民的收入与年龄、职业等方面的关系,必须按月收入再从这10 000人中用分层抽样方法抽出100人作进一步分析,则月收入在[2 500,3 000)的这段应抽多少人?
必修3第二章《统计》单元检测题参考答案
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
A
C
C
D
B
B
C
A
A
B
B
【第1题解析】抽出的号码是5,10,15,…,60,符合系统抽样的特点:“等距抽样”.故选B.
【第2题解析】根据题意,由系统抽样的方法规则,知:若在第三组中抽得号码为12的学生,则在第八组中抽得号码为的学生.故选A.
【第6题解析】840÷42=20,把1,2,…,840分成42段,不妨设第1段抽取的号码为l,则第k段抽取的号码为l+(k-1)·20,1≤l≤20,1≤k≤42.令481≤l+(k-1)·20≤720,得25+≤k≤37-.由1≤l≤20,则25≤k≤36.满足条件的k共有12个.故选B.
【第7题解析】由中位数的定义得选B,故选B.
【第8题解析】由频率分布直方图可知[25,30)的频率应为0.2,又[20,25)的频率为0.05,[30,35)的频率为0.35,计算可得中位数约为33.6,故选C.
【第9题解析】设中间长方形的面积等于S,则S=(1-S),S=,设中间一组的频数为x,则=,得x=32. 故选A.
【第10题解析】样本中小于29的数据频数为1+1+3+3+18+16=42.,所以小于29的数据大约占总体的×100%=42%. 故选A.
【第11题解析】设A,C产品数量分别为x件、y件,则由题意可得:所以所以故选B.
【第12题解析】因为=3,=5,又回归直线过点(,),所以5=3+,
所以=-. 故选B .
填空题答案
第13题
160
第14题
48
第15题
②③
第16题
42 3
【第15题解析】①平均成绩x甲=106,x乙=107,平均水平相近,不存在说乙班的数学成绩大大优于甲班.①错.②s=6,s=14,s<s,乙班数学成绩比甲班波动大. ②对;③s<s,甲班的数学成绩较乙班稳定,③对. 故填②③.
【第16题解析】由=42,得中位数是42. 母亲平均年龄=42.5,父亲平均年龄为45.5,因而父亲平均年龄比母亲平均年龄多3岁.故填42 3 .
【第17题答案】(1)51;(2)42.5 ;(3)中位数描述每天的用水量更合适.
【第17题解析】 (1)=(22+38+40+2×41+2×44+50+2×95)=51(吨).
(2)中位数为=42.5(吨).
(3)平均数受数据中的极端值(2个95)影响较大,使平均数在估计总体时可靠性降低,10天的用水量有8天都在平均值以下,故用中位数描述每天的用水量更合适.
【第18题答案】(1)茎叶图见解析;(2)乙种麦苗平均株高较高,甲种麦苗长得较为整齐.
【第18题解析】(1)茎叶图如图所示:
(2)甲==12,
乙==13,
s≈13.67,s≈16.67.
因为甲<乙,所以乙种麦苗平均株高较高,又因为s<s,所以甲种麦苗长得较为整齐.
s=[(78-85)2+(79-85)2+(81-85)2+(82-85)2+(84-85)2+(88-85)2+(93-85)2+(95-85)2]=35.5,
s=[(75-85)2+(80-85)2+(80-85)2+(83-85)2+(85-85)2+(90-85)2+(92-85)2+(95-85)2]=41.
∵甲=乙,s<s,
∴甲的成绩较稳定,派甲参赛比较合适.
【第20题答案】(1)6,79.86;(2)=51.36+4.75x,(3)每天多销售1件,纯利平均增加4.75元.
【第20题解析】(1)=(3+4+5+…+9)=6,
=(66+69+…+91)≈79.86.
(2)设回归直线方程为=+x,
则==≈4.75.
=- ≈79.86-4.75×6=51.36.
∴所求的回归直线方程为=51.36+4.75x.
(2)
分组
频数
频率
一组
0≤t<5
0
0
二组
5≤t<10
10
0.10
三组
10≤t<15
10
0.10
四组
15≤t<20
50
0.50
五组
20≤t<25
30
0.30
合计
100
1.00
(3)设旅客平均购票时间为s min,则有
≤
s<,
解得15≤s<20,
故旅客购票用时平均数可能落在第四小组.
(4)设需增加x个窗口,则20-5x≤10,解得x≥2,故至少需要增加2个窗口.
