第20讲:选修1-2第一章《统计案例》单元检测题-高中数学单元检测题 Word版含解析
文档属性
| 名称 | 第20讲:选修1-2第一章《统计案例》单元检测题-高中数学单元检测题 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 501.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-08 20:25:37 | ||
图片预览




文档简介
选修1-2第一章《统计案例》单元检测题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在两个变量的回归分析中,作散点图是为了( )
A.直接求出回归直线方程
B.直接求出回归方程
C.根据经验选定回归方程的类型
D.估计回归方程的参数
2.第二届世界青年奥林匹克运动会,中国获37金,13银,13铜共63枚奖牌居奖牌榜首位,并打破十项青奥会记录.由此许多人认为中国进入了世界体育强国之列,也有许多人持反对意见.有网友为此进行了调查,在参加调查的2 548名男性公民中有1 560名持反对意见,2 452名女性公民中有1 200人持反对意见,在运用这些数据说明中国的奖牌数是否与中国进入体育强国有无关系时,用什么方法最有说服力( )
A.平均数与方差 B.回归直线方程
C.独立性检验 D.概率
3. 某医学科研所对人体脂肪含量与年龄这两个变量研究得到一组随机样本数据,运用Excel软件计算得=0.577x-0.448(x为人的年龄,y%为人体脂肪含量).对年龄为37岁的人来说,下面说法正确的是( )
A.年龄为37岁的人体内脂肪含量都为20.90%
B.年龄为37岁的人体内脂肪含量为21.0%
C.年龄为37岁的人群中的大部分人的体内脂肪含量为20.90%
D.年龄为37岁的大部分的人体内脂肪含量为31.5%
4. 设有一个回归方程为=3-5x,当变量x增加一个单位时 ( )
A.y平均增加3个单位 B.y平均减少5个单位
C.y平均增加5个单位 D.y平均减少3个单位
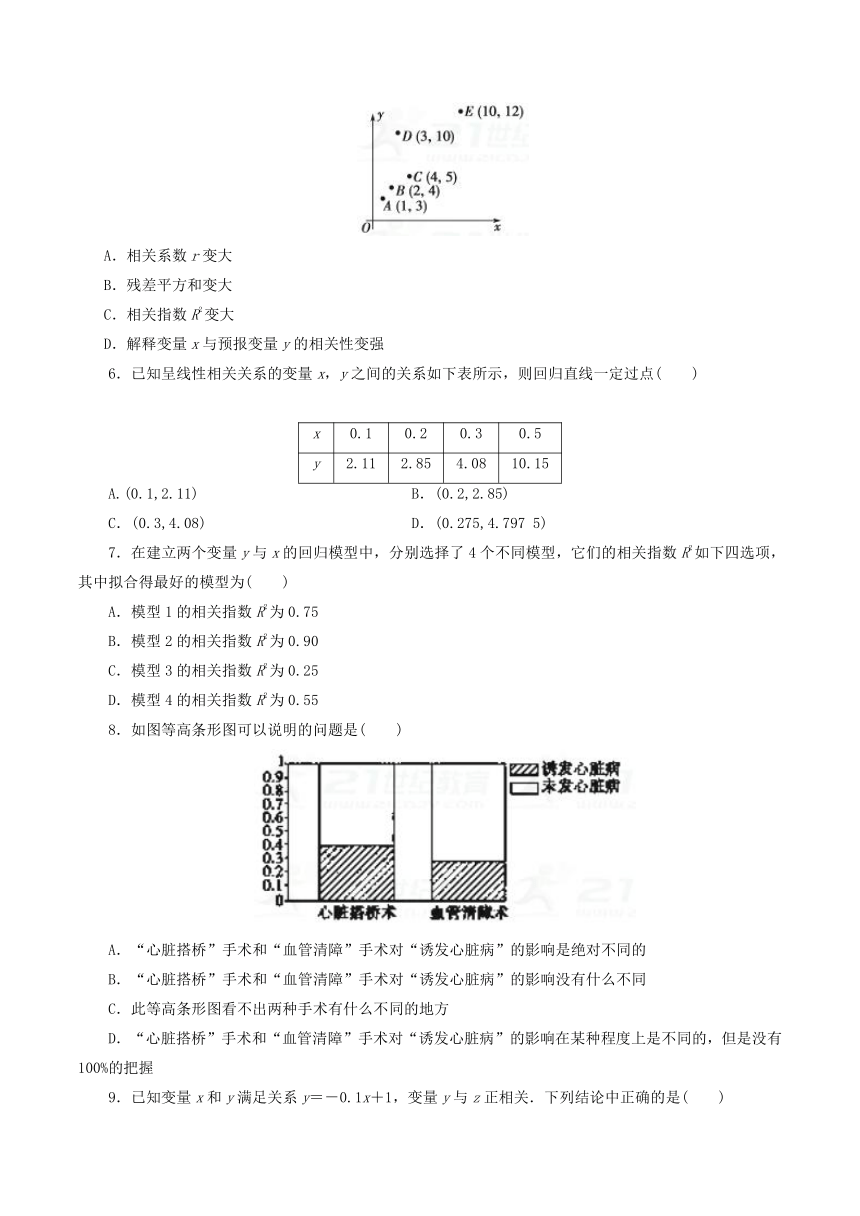
5.如图,5个(x,y)数据,去掉D(3,10)后,下列说法错误的是
( ).
A.相关系数r变大
B.残差平方和变大
C.相关指数R2变大
D.解释变量x与预报变量y的相关性变强
6.已知呈线性相关关系的变量x,y之间的关系如下表所示,则回归直线一定过点( )
x
0.1
0.2
0.3
0.5
y
2.11
2.85
4.08
10.15
A.(0.1,2.11) B.(0.2,2.85)
C.(0.3,4.08) D.(0.275,4.797 5)
7.在建立两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下四选项,其中拟合得最好的模型为( )
A.模型1的相关指数R2为0.75
B.模型2的相关指数R2为0.90
C.模型3的相关指数R2为0.25
D.模型4的相关指数R2为0.55
8.如图等高条形图可以说明的问题是( )
A.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响是绝对不同的
B.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响没有什么不同
C.此等高条形图看不出两种手术有什么不同的地方
D.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有100%的把握
9.已知变量x和y满足关系y=-0.1x+1,变量y与z正相关.下列结论中正确的是( )
A.x与y正相关,x与z负相关
B.x与y正相关,x与z正相关
C.x与y负相关,x与z负相关
D.x与y负相关,x与z正相关
10.观察两个变量(存在线性相关关系)得如下数据:
x
-10
-6.99
-5.01
-2.98
3.98
5
7.99
8.01
y
-9
-7
-5
-3
4.01
4.99
7
8
则两变量间的线性回归方程为( )
A.=x+1 B.=x
C.=2x+ D.=x+1
11. 根据如下所示的列联表得到如下四个判断:①在犯错误的概率不超过0.001的前提下认为患肝病与嗜酒有关;②在犯错误的概率不超过0.01的前提下认为患肝病与嗜酒有关;③认为患肝病与嗜酒有关的出错的可能为0.001%;④没有证据显示患肝病与嗜酒有关.
分类
嗜酒
不嗜酒
总计
患肝病
7 775
42
7 817
未患肝病
2 099
49
2 148
总计
9 874
91
9 965
其中正确命题的个数为( )
A.1 B.2
C.3 D.4
12. 有两个分类变量x与y,其一组观测值如2×2列联表所示:
y
x
y1
y2
x1
a
20-a
x2
15-a
30+a
其中a,15-a均为大于5的整数,若在犯错误的概率不超过0. 1的前提下认为x与y之间有关系,则a的值是( )
A.7 B.8
C.9 D.8或9
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.如果由一个2×2列联表中的数据计算得k=4.073,那么有__________的把握认为两变量有关系,已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.
14.某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未用血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算得K2≈3.918,经查对临界值表知P(K2≥3.841)≈0.05,对此,四名同学作出了以下的判断:
p:有95%的把握认为“能起到预防感冒的作用”;
q:如果某人未使用该血清,那么他在一年中有95%的可能性得感冒:
r:这种血清预防感冒的有效率为95%;
s:这种血清预防感冒的有效率为5%.
则下列结论中,正确结论的序号是__________.
(1)p∧非q;(2) 非p∧q;(3)( 非p∧非q)∧(r∨s);(4)(p∨非r)∧(非q∨s).
15.调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加__________万元.
16.某数学老师身高176 cm,他爷爷、父亲和儿子的身高分别是173 cm,170 cm和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为__________cm.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)抽测了10名15岁男生的身高x(单位:cm)和体重y(单位:kg),得到如下数据:
x
157
153
151
158
156
159
160
158
160
162
y
45.5
44
42
46
44.5
45
46.5
47
45
49
(1)画出散点图;
(2)你能从散点图中发现身高与体重近似成什么关系吗?
(3)如果近似成线性关系,试画出一条直线来近似地表示这种关系.
18.(本小题满分12分)某班5名学生的数学和物理成绩如下表:
学生
学科
A
B
C
D
E
数学成绩(x)
88
76
73
66
63
物理成绩(y)
78
65
71
64
61
(1)画出散点图;
(2)求物理成绩y对数学成绩x的线性回归方程;
(3)一名学生的数学成绩是96分,试预测他的物理成绩.
19.(本小题满分12分)某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作
不太主动参加班级工作
合计
学习积极性高
18
7
25
学习积极性一般
6
19
25
合计
24
26
50
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由?
20.(本小题满分14分)研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得的数据如下表:
刹车时的车速(km/h)
0
10
20
30
40
50
60
刹车距离(m)
0
0.3
1.0
2.1
3.6
5.5
7.8
(1)以车速为x轴,以刹车距离为y轴,在给定坐标系中画出这些数据的散点图;
(2)观察散点图,估计函数的类型,并确定一个满足这些数据的函数表达式;
(3)该型号汽车在国道上发生了一次交通事故,现场测得刹车距离为46.5 m,请推测刹车时的速度为多少?请问在事故发生时,汽车是超速行驶还是正常行驶?
21.(本小题满分12分)某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日期
温差
12月1日
12月2日
12月3日
12月4日
12月5日
x(℃)
10
11
13
12
8
发芽数y(颗)
23
25
30
26
16
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程 = x+ ;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
22.(本小题满分12分)为了调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别
是否需要志愿者
男
女
需要
40
30
不需要
160
270
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关;
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由?
附:
0.050
0.010
0.001
3.841
6.635
10.828
K2=
选修1-2第一章《统计案例》单元检测题参考答案
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
C
B
B
D
B
D
C
B
B
D
【第4题解析】-5是斜率的估计值,说明x每增加一个单位,y平均减少5个单位.故选B.
【第5题解析】由题中散点图知,去掉D后,x与y的相关性变强,且为正相关,所以r变大,R2变大,残差平方和变小.故选B.
【第6题解析】回归直线一定过点(,),通过表格中的数据计算出和,故选D.
【第7题解析】相关指数R2的值越大,意味着残差平方和越小,也就是说模型的拟合效果越好,故选B.
【第8题解析】由等高条件形图知,D正确.故选D.
【第9题解析】因为y=-0.1x+1的斜率小于0,故x与y负相关.因为y与z正相关,可设z=y+,>0,则z=y+=-0.1x++,故x与z负相关.故选C.
【第10解析】由于线性回归方程一定经过样本点的中心(,),所以本题只需求出,,然后代入所给选项进行检验,即可得到答案.由表中数据可得,=0,=0,只有B项中的方程过(0,0)点,故选B.
【第11题解析】由列联表可求K2的观测值k=
=≈56.632 由56.632>10.828>6.635.
且P(K2≥10.828)=0.001,P(K2≥6.635)=0.010. ∴①,②均正确.故选B.
【第12题解析】查表可知,要使在犯错误的概率不超过0.1的前提下认为x与y之间有关系,则k≥2.706,而k===. 由k≥2.706得a≥7. 19或a≤2.04.又a>5且15-a>5,a∈Z,即a=8或9.故选D.
填空题答案
第13题
95%
第14题
(1)(4)
第15题
0.254
第16题
185
【第16题解析】根据题意列表如下:身高y(单位:cm)
x
1
2
3
4
y
170
173
176
182
xiyi=1 772,=,=+170,x=30,所以===3.9,=-=+170-3.9×=165.5,所以线性回归方程为=x+=3.9x+165.5,将x=5代入得该老师孙子的身高估计值为3.9×5+165.5=185 cm.故填185.
【第17题答案】(1)见解析;(2)身高与体重线性相关;(3)见解析.
【第17题解析】(1)散点图如下图所示:
(2)从散点图可知,当身高增加时,体重也增加,而且这些点在一条直线附近摆动,因此身高与体重线性相关.
(3)作出直线如下图所示.
(2)=×(88+76+73+66+63)=73.2.
=×(78+65+71+64+61)=67.8.
iyi=88×78+76×65+73×71+66×64+63×61=25 054.
=882+762+732+662+632=27 174.
∴=≈0.625.
∴=-=67.8-0.625×73.2=22.05.
∴y对x的线性回归方程是=0.625x+22.05.
(3)当x=96,则=0.625×96+22.05≈82.
所以预测他的物理成绩是82分.
(2)由表中数据可得
K2==≈11.5>10.828,
∴有99.9%的把握说学习积极性与对待班级工作的态度有关系.
【第20题答案】(1)见解析; (2) 函数的表达式为y=0.002x2+0.01x(0≤x≤140); (3) 因此发生事故时,汽车属于超速行驶.
【第20题解析】(1)散点图如图表示:
(2)由图象,设函数的表达式为y=ax2+bx+c(a≠0),将(0,0),(10,0.3)( 20,1.0)代入,得
解得a=0.002,b=0.01,c=0.
所以,函数的表达式为y=0.002x2+0.01x(0≤x≤140).
经检验,表中其他各值也符合此表达式.
(3)当y=46.5时,即0.002x2+0.01x=46.5,
所以x2+5x-23 250=0.
解得x1=150,x2=-155(舍去).
故可推测刹车时的速度为150 km/h,而150>140,
因此发生事故时,汽车属于超速行驶.
(2)由数据,求得=12,=27,
由公式,求得 =, =- =-3.
所以y关于x的线性回归方程为 =x-3.
(3)当x=10时, =×10-3=22,|22-23|<2;
同样,当x=8时, =×8-3=17,|17-16|<2.
所以,该研究所得到的线性回归方程是可靠的.
【第22题答案】(1)14%;(2)有99%的把握认为该地区的老年人是否需要帮助与性别有关;(3)见解析.
【第22题解析】(1)调查的500位老年人中,有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例的估计值为=14%.
(2)K2=≈9.967.
由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.
(3)由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据可以看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异.因此,在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层,并采用分层抽样方法比采用简单随机抽样方法更好.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.在两个变量的回归分析中,作散点图是为了( )
A.直接求出回归直线方程
B.直接求出回归方程
C.根据经验选定回归方程的类型
D.估计回归方程的参数
2.第二届世界青年奥林匹克运动会,中国获37金,13银,13铜共63枚奖牌居奖牌榜首位,并打破十项青奥会记录.由此许多人认为中国进入了世界体育强国之列,也有许多人持反对意见.有网友为此进行了调查,在参加调查的2 548名男性公民中有1 560名持反对意见,2 452名女性公民中有1 200人持反对意见,在运用这些数据说明中国的奖牌数是否与中国进入体育强国有无关系时,用什么方法最有说服力( )
A.平均数与方差 B.回归直线方程
C.独立性检验 D.概率
3. 某医学科研所对人体脂肪含量与年龄这两个变量研究得到一组随机样本数据,运用Excel软件计算得=0.577x-0.448(x为人的年龄,y%为人体脂肪含量).对年龄为37岁的人来说,下面说法正确的是( )
A.年龄为37岁的人体内脂肪含量都为20.90%
B.年龄为37岁的人体内脂肪含量为21.0%
C.年龄为37岁的人群中的大部分人的体内脂肪含量为20.90%
D.年龄为37岁的大部分的人体内脂肪含量为31.5%
4. 设有一个回归方程为=3-5x,当变量x增加一个单位时 ( )
A.y平均增加3个单位 B.y平均减少5个单位
C.y平均增加5个单位 D.y平均减少3个单位
5.如图,5个(x,y)数据,去掉D(3,10)后,下列说法错误的是
( ).
A.相关系数r变大
B.残差平方和变大
C.相关指数R2变大
D.解释变量x与预报变量y的相关性变强
6.已知呈线性相关关系的变量x,y之间的关系如下表所示,则回归直线一定过点( )
x
0.1
0.2
0.3
0.5
y
2.11
2.85
4.08
10.15
A.(0.1,2.11) B.(0.2,2.85)
C.(0.3,4.08) D.(0.275,4.797 5)
7.在建立两个变量y与x的回归模型中,分别选择了4个不同模型,它们的相关指数R2如下四选项,其中拟合得最好的模型为( )
A.模型1的相关指数R2为0.75
B.模型2的相关指数R2为0.90
C.模型3的相关指数R2为0.25
D.模型4的相关指数R2为0.55
8.如图等高条形图可以说明的问题是( )
A.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响是绝对不同的
B.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响没有什么不同
C.此等高条形图看不出两种手术有什么不同的地方
D.“心脏搭桥”手术和“血管清障”手术对“诱发心脏病”的影响在某种程度上是不同的,但是没有100%的把握
9.已知变量x和y满足关系y=-0.1x+1,变量y与z正相关.下列结论中正确的是( )
A.x与y正相关,x与z负相关
B.x与y正相关,x与z正相关
C.x与y负相关,x与z负相关
D.x与y负相关,x与z正相关
10.观察两个变量(存在线性相关关系)得如下数据:
x
-10
-6.99
-5.01
-2.98
3.98
5
7.99
8.01
y
-9
-7
-5
-3
4.01
4.99
7
8
则两变量间的线性回归方程为( )
A.=x+1 B.=x
C.=2x+ D.=x+1
11. 根据如下所示的列联表得到如下四个判断:①在犯错误的概率不超过0.001的前提下认为患肝病与嗜酒有关;②在犯错误的概率不超过0.01的前提下认为患肝病与嗜酒有关;③认为患肝病与嗜酒有关的出错的可能为0.001%;④没有证据显示患肝病与嗜酒有关.
分类
嗜酒
不嗜酒
总计
患肝病
7 775
42
7 817
未患肝病
2 099
49
2 148
总计
9 874
91
9 965
其中正确命题的个数为( )
A.1 B.2
C.3 D.4
12. 有两个分类变量x与y,其一组观测值如2×2列联表所示:
y
x
y1
y2
x1
a
20-a
x2
15-a
30+a
其中a,15-a均为大于5的整数,若在犯错误的概率不超过0. 1的前提下认为x与y之间有关系,则a的值是( )
A.7 B.8
C.9 D.8或9
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.如果由一个2×2列联表中的数据计算得k=4.073,那么有__________的把握认为两变量有关系,已知P(K2≥3.841)≈0.05,P(K2≥5.024)≈0.025.
14.某医疗研究所为了检验某种血清预防感冒的作用,把500名使用血清的人与另外500名未用血清的人一年中的感冒记录作比较,提出假设H0:“这种血清不能起到预防感冒的作用”,利用2×2列联表计算得K2≈3.918,经查对临界值表知P(K2≥3.841)≈0.05,对此,四名同学作出了以下的判断:
p:有95%的把握认为“能起到预防感冒的作用”;
q:如果某人未使用该血清,那么他在一年中有95%的可能性得感冒:
r:这种血清预防感冒的有效率为95%;
s:这种血清预防感冒的有效率为5%.
则下列结论中,正确结论的序号是__________.
(1)p∧非q;(2) 非p∧q;(3)( 非p∧非q)∧(r∨s);(4)(p∨非r)∧(非q∨s).
15.调查了某地若干户家庭的年收入x(单位:万元)和年饮食支出y(单位:万元),调查显示年收入x与年饮食支出y具有线性相关关系,并由调查数据得到y对x的回归直线方程:=0.254x+0.321.由回归直线方程可知,家庭年收入每增加1万元,年饮食支出平均增加__________万元.
16.某数学老师身高176 cm,他爷爷、父亲和儿子的身高分别是173 cm,170 cm和182 cm.因儿子的身高与父亲的身高有关,该老师用线性回归分析的方法预测他孙子的身高为__________cm.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分12分)抽测了10名15岁男生的身高x(单位:cm)和体重y(单位:kg),得到如下数据:
x
157
153
151
158
156
159
160
158
160
162
y
45.5
44
42
46
44.5
45
46.5
47
45
49
(1)画出散点图;
(2)你能从散点图中发现身高与体重近似成什么关系吗?
(3)如果近似成线性关系,试画出一条直线来近似地表示这种关系.
18.(本小题满分12分)某班5名学生的数学和物理成绩如下表:
学生
学科
A
B
C
D
E
数学成绩(x)
88
76
73
66
63
物理成绩(y)
78
65
71
64
61
(1)画出散点图;
(2)求物理成绩y对数学成绩x的线性回归方程;
(3)一名学生的数学成绩是96分,试预测他的物理成绩.
19.(本小题满分12分)某班主任对全班50名学生学习积极性和对待班级工作的态度进行了调查,统计数据如下表所示:
积极参加班级工作
不太主动参加班级工作
合计
学习积极性高
18
7
25
学习积极性一般
6
19
25
合计
24
26
50
(1)如果随机抽查这个班的一名学生,那么抽到积极参加班级工作的学生的概率是多少?抽到不太主动参加班级工作且学习积极性一般的学生的概率是多少?
(2)试运用独立性检验的思想方法分析:学生的学习积极性与对待班级工作的态度是否有关系?并说明理由?
20.(本小题满分14分)研究“刹车距离”对于安全行车及分析交通事故责任都有一定的作用,所谓“刹车距离”就是指行驶中的汽车,从刹车开始到停止,由于惯性的作用而又继续向前滑行的一段距离.为了测定某种型号汽车的刹车性能(车速不超过140 km/h),对这种汽车进行测试,测得的数据如下表:
刹车时的车速(km/h)
0
10
20
30
40
50
60
刹车距离(m)
0
0.3
1.0
2.1
3.6
5.5
7.8
(1)以车速为x轴,以刹车距离为y轴,在给定坐标系中画出这些数据的散点图;
(2)观察散点图,估计函数的类型,并确定一个满足这些数据的函数表达式;
(3)该型号汽车在国道上发生了一次交通事故,现场测得刹车距离为46.5 m,请推测刹车时的速度为多少?请问在事故发生时,汽车是超速行驶还是正常行驶?
21.(本小题满分12分)某农科所对冬季昼夜温差大小与某反季节大豆新品种发芽多少之间的关系进行分析研究,他们分别记录了12月1日至12月5日的每天昼夜温差与实验室每天每100颗种子中的发芽数,得到如下资料:
日期
温差
12月1日
12月2日
12月3日
12月4日
12月5日
x(℃)
10
11
13
12
8
发芽数y(颗)
23
25
30
26
16
该农科所确定的研究方案是:先从这五组数据中选取2组,用剩下的3组数据求线性回归方程,再对被选取的2组数据进行检验.
(1)求选取的2组数据恰好是不相邻2天数据的概率;
(2)若选取的是12月1日与12月5日的两组数据,请根据12月2日至12月4日的数据,求出y关于x的线性回归方程 = x+ ;
(3)若由线性回归方程得到的估计数据与所选出的检验数据的误差均不超过2颗,则认为得到的线性回归方程是可靠的,试问(2)中所得的线性回归方程是否可靠?
22.(本小题满分12分)为了调查某地区老年人是否需要志愿者提供帮助,用简单随机抽样方法从该地区调查了500位老年人,结果如下:
性别
是否需要志愿者
男
女
需要
40
30
不需要
160
270
(1)估计该地区老年人中,需要志愿者提供帮助的老年人的比例;
(2)能否有99%的把握认为该地区的老年人是否需要志愿者提供帮助与性别有关;
(3)根据(2)的结论,能否提出更好的调查方法来估计该地区的老年人中,需要志愿者提供帮助的老年人的比例?说明理由?
附:
0.050
0.010
0.001
3.841
6.635
10.828
K2=
选修1-2第一章《统计案例》单元检测题参考答案
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
C
C
C
B
B
D
B
D
C
B
B
D
【第4题解析】-5是斜率的估计值,说明x每增加一个单位,y平均减少5个单位.故选B.
【第5题解析】由题中散点图知,去掉D后,x与y的相关性变强,且为正相关,所以r变大,R2变大,残差平方和变小.故选B.
【第6题解析】回归直线一定过点(,),通过表格中的数据计算出和,故选D.
【第7题解析】相关指数R2的值越大,意味着残差平方和越小,也就是说模型的拟合效果越好,故选B.
【第8题解析】由等高条件形图知,D正确.故选D.
【第9题解析】因为y=-0.1x+1的斜率小于0,故x与y负相关.因为y与z正相关,可设z=y+,>0,则z=y+=-0.1x++,故x与z负相关.故选C.
【第10解析】由于线性回归方程一定经过样本点的中心(,),所以本题只需求出,,然后代入所给选项进行检验,即可得到答案.由表中数据可得,=0,=0,只有B项中的方程过(0,0)点,故选B.
【第11题解析】由列联表可求K2的观测值k=
=≈56.632 由56.632>10.828>6.635.
且P(K2≥10.828)=0.001,P(K2≥6.635)=0.010. ∴①,②均正确.故选B.
【第12题解析】查表可知,要使在犯错误的概率不超过0.1的前提下认为x与y之间有关系,则k≥2.706,而k===. 由k≥2.706得a≥7. 19或a≤2.04.又a>5且15-a>5,a∈Z,即a=8或9.故选D.
填空题答案
第13题
95%
第14题
(1)(4)
第15题
0.254
第16题
185
【第16题解析】根据题意列表如下:身高y(单位:cm)
x
1
2
3
4
y
170
173
176
182
xiyi=1 772,=,=+170,x=30,所以===3.9,=-=+170-3.9×=165.5,所以线性回归方程为=x+=3.9x+165.5,将x=5代入得该老师孙子的身高估计值为3.9×5+165.5=185 cm.故填185.
【第17题答案】(1)见解析;(2)身高与体重线性相关;(3)见解析.
【第17题解析】(1)散点图如下图所示:
(2)从散点图可知,当身高增加时,体重也增加,而且这些点在一条直线附近摆动,因此身高与体重线性相关.
(3)作出直线如下图所示.
(2)=×(88+76+73+66+63)=73.2.
=×(78+65+71+64+61)=67.8.
iyi=88×78+76×65+73×71+66×64+63×61=25 054.
=882+762+732+662+632=27 174.
∴=≈0.625.
∴=-=67.8-0.625×73.2=22.05.
∴y对x的线性回归方程是=0.625x+22.05.
(3)当x=96,则=0.625×96+22.05≈82.
所以预测他的物理成绩是82分.
(2)由表中数据可得
K2==≈11.5>10.828,
∴有99.9%的把握说学习积极性与对待班级工作的态度有关系.
【第20题答案】(1)见解析; (2) 函数的表达式为y=0.002x2+0.01x(0≤x≤140); (3) 因此发生事故时,汽车属于超速行驶.
【第20题解析】(1)散点图如图表示:
(2)由图象,设函数的表达式为y=ax2+bx+c(a≠0),将(0,0),(10,0.3)( 20,1.0)代入,得
解得a=0.002,b=0.01,c=0.
所以,函数的表达式为y=0.002x2+0.01x(0≤x≤140).
经检验,表中其他各值也符合此表达式.
(3)当y=46.5时,即0.002x2+0.01x=46.5,
所以x2+5x-23 250=0.
解得x1=150,x2=-155(舍去).
故可推测刹车时的速度为150 km/h,而150>140,
因此发生事故时,汽车属于超速行驶.
(2)由数据,求得=12,=27,
由公式,求得 =, =- =-3.
所以y关于x的线性回归方程为 =x-3.
(3)当x=10时, =×10-3=22,|22-23|<2;
同样,当x=8时, =×8-3=17,|17-16|<2.
所以,该研究所得到的线性回归方程是可靠的.
【第22题答案】(1)14%;(2)有99%的把握认为该地区的老年人是否需要帮助与性别有关;(3)见解析.
【第22题解析】(1)调查的500位老年人中,有70位需要志愿者提供帮助,因此该地区老年人中,需要帮助的老年人的比例的估计值为=14%.
(2)K2=≈9.967.
由于9.967>6.635,所以有99%的把握认为该地区的老年人是否需要帮助与性别有关.
(3)由(2)的结论知,该地区老年人是否需要帮助与性别有关,并且从样本数据可以看出该地区男性老年人与女性老年人中需要帮助的比例有明显差异.因此,在调查时,先确定该地区老年人中男、女的比例,再把老年人分成男、女两层,并采用分层抽样方法比采用简单随机抽样方法更好.
