第04讲:必修2第一章《空间几何体》单元检测题-高中数学单元检测题 Word版含解析
文档属性
| 名称 | 第04讲:必修2第一章《空间几何体》单元检测题-高中数学单元检测题 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 557.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-08 20:35:07 | ||
图片预览


文档简介
必修2第一章《空间几何体》单元检测题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)
1.以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于
( )
A.2π
B.π
C.2
D.1
2.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为
( )
A.18+36
B.54+18
C.90
D.81
3.已知一个底面是菱形、侧面是矩形的四棱柱,侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是
( )
A.30
B.60
C.30+135
D.135
4.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V1和V2,则V1:V2=
( )
A.1:3
B.1:1
C.2:1
D.3:1
5.若两个球的表面积之比为1:4,则这两个球的体积之比为
( )
A.1:2
B.1:4
C.1:8
D.1:16
6.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积为
( )
A.6
B.3
C.6
D.12
7.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为
( )
A.1
B.
C.
D.2
8.若一圆柱与圆锥的高相等,且轴截面面积也相等,那么圆柱与圆锥的体积之比为
( )
A.1
B.
C.
D.
9.半径为R的半圆卷成一个圆锥,则它的体积为
( )
D.πR3
B.πR3
C.πR3
D.πR3
10.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有
( )
A.14斛
B.22斛
C.36斛
D.66斛
11.已知底面为正三角形,侧面为矩形的三棱柱有一个半径为
cm的内切球,则此棱柱的体积是
( )
A.9
cm3
B.54
cm3
C.27
cm3
D.18
cm3
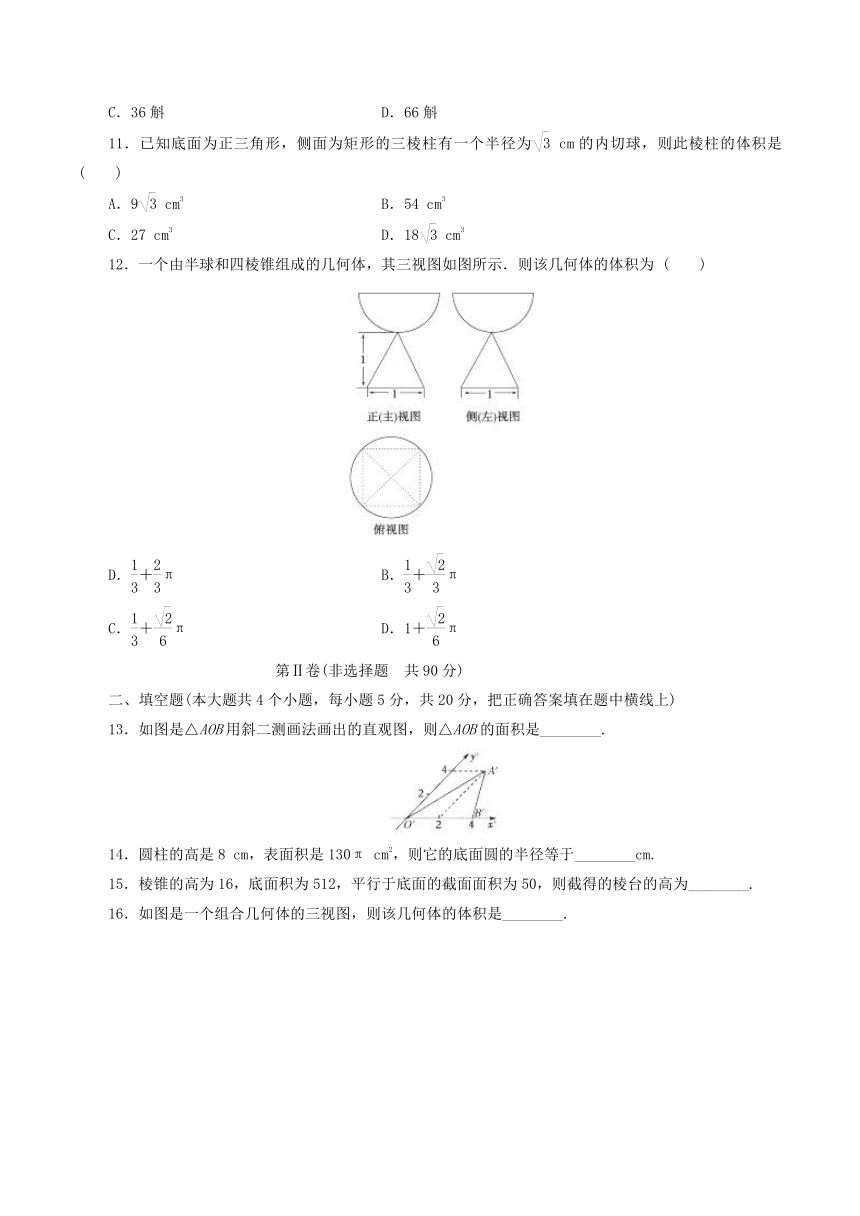
12.一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为
( )
D.+π
B.+π
C.+π
D.1+π
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.如图是△AOB用斜二测画法画出的直观图,则△AOB的面积是________.
14.圆柱的高是8
cm,表面积是130π
cm2,则它的底面圆的半径等于________cm.
15.棱锥的高为16,底面积为512,平行于底面的截面面积为50,则截得的棱台的高为________.
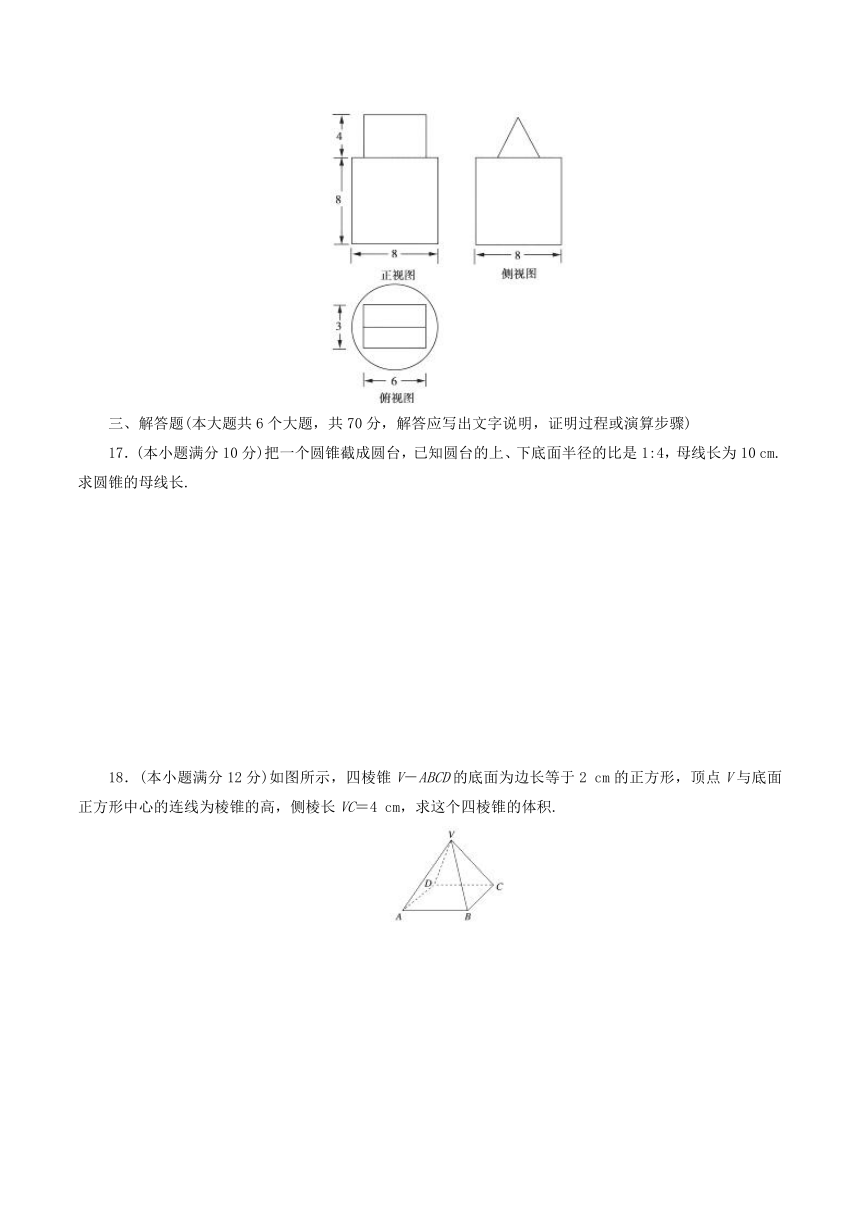
16.如图是一个组合几何体的三视图,则该几何体的体积是________.
三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长为10
cm.求圆锥的母线长.
18.(本小题满分12分)如图所示,四棱锥V-ABCD的底面为边长等于2
cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4
cm,求这个四棱锥的体积.
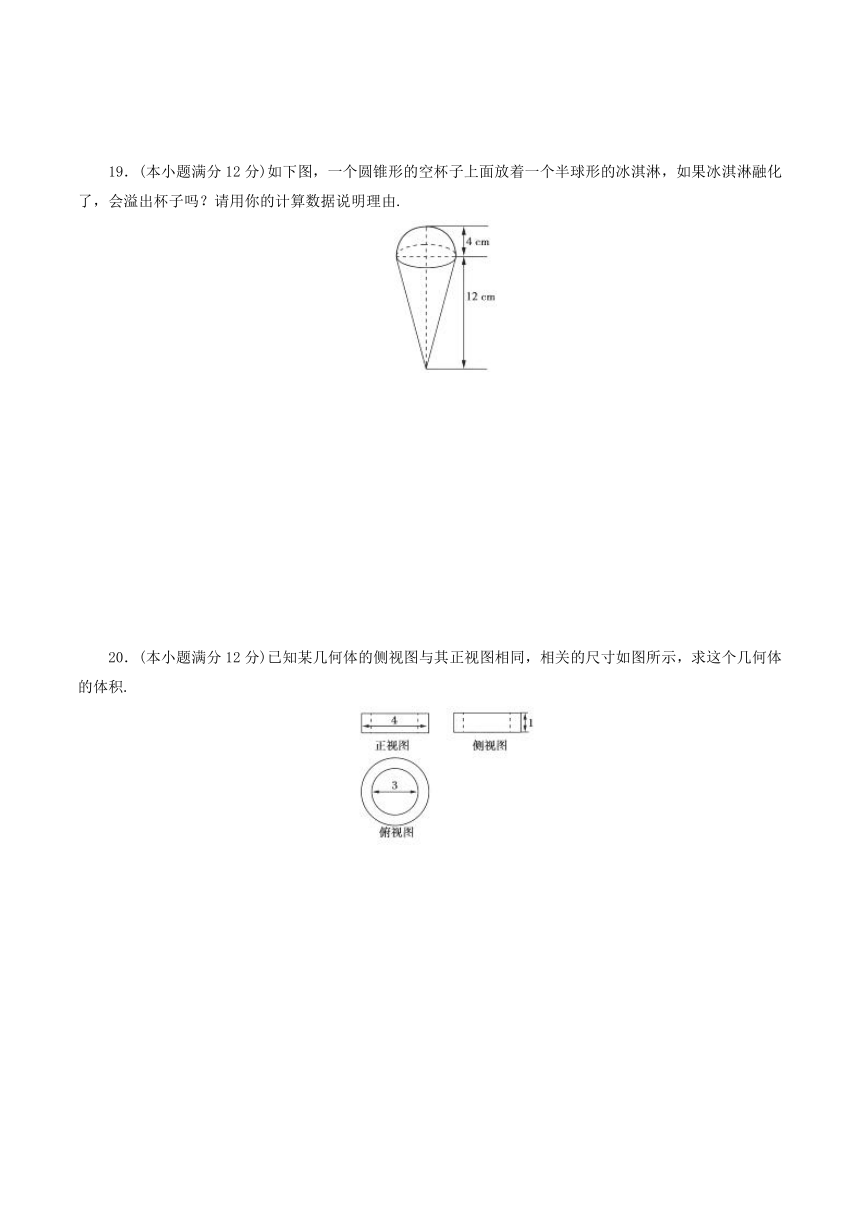
19.(本小题满分12分)如下图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.
20.(本小题满分12分)已知某几何体的侧视图与其正视图相同,相关的尺寸如图所示,求这个几何体的体积.
21.(本小题满分12分)据说伟大的阿基米德逝世后,敌军将领马塞拉斯给他建了一块墓碑,在墓碑上刻了一个如图所示的图案,图案中球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.试计算出图案中圆锥、球、圆柱的体积比.
22.(本小题满分12分)如图所示,有一块扇形铁皮OAB,∠AOB=60°,OA=72
cm,要剪下来一个扇形环ABCD,作圆台形容器的侧面,并且余下的扇形OCD内剪下一块与其相切的圆形使它恰好作圆台形容器的下底面(大底面).
试求:(1)AD的长;(2)容器的容积.
必修2第一章《空间几何体》单元检测题
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
A
D
C
D
C
D
A
B
B
C
【第1题解析】所得旋转体是底面半径为1,高为1的圆柱,其侧面积S侧=2πRh=2π×1×1=2π.
故选A.
【第2题解析】由三视图,知该几何体是一个斜四棱柱,所以该几何体的表面积S=2×3×6+2×3×3+2×3×3=54+18,故选B.
【第5题解析】设两个球的半径分别为r1、r2,∴S1=4πr,S2=4πr.
∴==,∴=.
∴==()3=.
故选C
.
【第6题解析】△OAB是直角三角形,OA=6,OB=4,∠AOB=90°,∴S△OAB=×6×4=12.
故选D.
【第7题解析】根据三视图,可知几何体的直观图为如图所示的四棱锥V-ABCD,其中VB⊥平面ABCD,且底面ABCD是边长为1的正方形,VB=1.所以四棱锥中最长棱为VD.
连接BD,易知BD=,在Rt△VBD中,VD==.
故选C
.
【第8题解析】设圆柱与圆锥的底半径分别为R,
r,高都是h,由题设,2R·h=×2r·h,
∴r=2R,V柱=πR2h,V锥=πr2h=πR2h,∴=,故选D.
【第9题解析】依题意,得圆锥的底面周长为πR,母线长为R,则底面半径为,高为R,所以圆锥的体积为×π×()2×R=πR3.
故选A
.
【第10题解析】设圆锥底面半径为r,则×2×3r=8,∴r=,所以米堆的体积为××3×()2×5=,故堆放的米约为÷1.62≈22,故选B.
【第11题解析】由题意知棱柱的高为2
cm,底面正三角形的内切圆的半径为
cm,∴底面正三角形的边长为6
cm,正三棱柱的底面面积为9
cm2,∴此三棱柱的体积V=9×2=54(cm3).故选B
.
【第12题解析】根据三视图可知,四棱锥的底面是边长为1的正方形、高是1,半球的半径为,所以该几何体的体积为×1×1×1+×π()3=+π.
故选C
.
填空题答案
第13题
16
第14题
5
第15题
11
第16题
(1,+∞)
【第16题解析】由三视图可知该组合几何体下面是一个圆柱,上面是一个三棱柱,故所求体积为V=×3×4×6+16π×8=36+128π.
故填36+128π.
【第17题答案】
cm
【第17题解析】如图,设圆锥母线长为l,则=,所以l=
cm.
【第18题答案】
cm3
【第18题解析】如图,连接AC、BD相交于点O,连接VO,
∵AB=BC=2
cm,
在正方形ABCD中,
求得CO=
cm,
又在直角三角形VOC中,
求得VO=
cm,
∴VV-ABCD=SABCD·VO=×4×=(cm3).
故这个四棱锥的体积为
cm3.
【第20题答案】
.
【第20题解析】由三视图可知,该几何体是大圆柱内挖掉了小圆柱,两个圆柱高均为1,底面是半径为2和的同心圆,故该几何体的体积为4π×1-π()2×1=.
【第21题答案】1:2:3.
【第21题解析】设圆柱的底面半径为r,高为h,则V圆柱=πr2h.
由题意知圆锥的底面半径为r,高为h,球的半径为r,
∴V圆锥=πr2h,
∴V球=πr3.
又h=2r,
∴V圆锥:V球:V圆柱=(πr2h):(πr3):(πr2h)=(πr3):(πr3):(2πr3)=1:2:3.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的)
1.以边长为1的正方形的一边所在直线为旋转轴,将该正方形旋转一周所得圆柱的侧面积等于
( )
A.2π
B.π
C.2
D.1
2.如图,网格纸上小正方形的边长为1,粗实线画出的是某多面体的三视图,则该多面体的表面积为
( )
A.18+36
B.54+18
C.90
D.81
3.已知一个底面是菱形、侧面是矩形的四棱柱,侧棱长为5,菱形的对角线的长分别是9和15,则这个棱柱的侧面积是
( )
A.30
B.60
C.30+135
D.135
4.已知圆柱与圆锥的底面积相等,高也相等,它们的体积分别为V1和V2,则V1:V2=
( )
A.1:3
B.1:1
C.2:1
D.3:1
5.若两个球的表面积之比为1:4,则这两个球的体积之比为
( )
A.1:2
B.1:4
C.1:8
D.1:16
6.如图,△O′A′B′是水平放置的△OAB的直观图,则△OAB的面积为
( )
A.6
B.3
C.6
D.12
7.某四棱锥的三视图如图所示,该四棱锥最长棱的棱长为
( )
A.1
B.
C.
D.2
8.若一圆柱与圆锥的高相等,且轴截面面积也相等,那么圆柱与圆锥的体积之比为
( )
A.1
B.
C.
D.
9.半径为R的半圆卷成一个圆锥,则它的体积为
( )
D.πR3
B.πR3
C.πR3
D.πR3
10.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周八尺,高五尺.问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图,米堆为一个圆锥的四分之一),米堆底部的弧度为8尺,米堆的高为5尺,问米堆的体积和堆放的米各为多少?”已知1斛米的体积约为1.62立方尺,圆周率约为3,估算出堆放斛的米约有
( )
A.14斛
B.22斛
C.36斛
D.66斛
11.已知底面为正三角形,侧面为矩形的三棱柱有一个半径为
cm的内切球,则此棱柱的体积是
( )
A.9
cm3
B.54
cm3
C.27
cm3
D.18
cm3
12.一个由半球和四棱锥组成的几何体,其三视图如图所示.则该几何体的体积为
( )
D.+π
B.+π
C.+π
D.1+π
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.如图是△AOB用斜二测画法画出的直观图,则△AOB的面积是________.
14.圆柱的高是8
cm,表面积是130π
cm2,则它的底面圆的半径等于________cm.
15.棱锥的高为16,底面积为512,平行于底面的截面面积为50,则截得的棱台的高为________.
16.如图是一个组合几何体的三视图,则该几何体的体积是________.
三、解答题(本大题共6个大题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)把一个圆锥截成圆台,已知圆台的上、下底面半径的比是1:4,母线长为10
cm.求圆锥的母线长.
18.(本小题满分12分)如图所示,四棱锥V-ABCD的底面为边长等于2
cm的正方形,顶点V与底面正方形中心的连线为棱锥的高,侧棱长VC=4
cm,求这个四棱锥的体积.
19.(本小题满分12分)如下图,一个圆锥形的空杯子上面放着一个半球形的冰淇淋,如果冰淇淋融化了,会溢出杯子吗?请用你的计算数据说明理由.
20.(本小题满分12分)已知某几何体的侧视图与其正视图相同,相关的尺寸如图所示,求这个几何体的体积.
21.(本小题满分12分)据说伟大的阿基米德逝世后,敌军将领马塞拉斯给他建了一块墓碑,在墓碑上刻了一个如图所示的图案,图案中球的直径与圆柱底面的直径和圆柱的高相等,圆锥的顶点为圆柱上底面的圆心,圆锥的底面是圆柱的下底面.试计算出图案中圆锥、球、圆柱的体积比.
22.(本小题满分12分)如图所示,有一块扇形铁皮OAB,∠AOB=60°,OA=72
cm,要剪下来一个扇形环ABCD,作圆台形容器的侧面,并且余下的扇形OCD内剪下一块与其相切的圆形使它恰好作圆台形容器的下底面(大底面).
试求:(1)AD的长;(2)容器的容积.
必修2第一章《空间几何体》单元检测题
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
A
B
A
D
C
D
C
D
A
B
B
C
【第1题解析】所得旋转体是底面半径为1,高为1的圆柱,其侧面积S侧=2πRh=2π×1×1=2π.
故选A.
【第2题解析】由三视图,知该几何体是一个斜四棱柱,所以该几何体的表面积S=2×3×6+2×3×3+2×3×3=54+18,故选B.
【第5题解析】设两个球的半径分别为r1、r2,∴S1=4πr,S2=4πr.
∴==,∴=.
∴==()3=.
故选C
.
【第6题解析】△OAB是直角三角形,OA=6,OB=4,∠AOB=90°,∴S△OAB=×6×4=12.
故选D.
【第7题解析】根据三视图,可知几何体的直观图为如图所示的四棱锥V-ABCD,其中VB⊥平面ABCD,且底面ABCD是边长为1的正方形,VB=1.所以四棱锥中最长棱为VD.
连接BD,易知BD=,在Rt△VBD中,VD==.
故选C
.
【第8题解析】设圆柱与圆锥的底半径分别为R,
r,高都是h,由题设,2R·h=×2r·h,
∴r=2R,V柱=πR2h,V锥=πr2h=πR2h,∴=,故选D.
【第9题解析】依题意,得圆锥的底面周长为πR,母线长为R,则底面半径为,高为R,所以圆锥的体积为×π×()2×R=πR3.
故选A
.
【第10题解析】设圆锥底面半径为r,则×2×3r=8,∴r=,所以米堆的体积为××3×()2×5=,故堆放的米约为÷1.62≈22,故选B.
【第11题解析】由题意知棱柱的高为2
cm,底面正三角形的内切圆的半径为
cm,∴底面正三角形的边长为6
cm,正三棱柱的底面面积为9
cm2,∴此三棱柱的体积V=9×2=54(cm3).故选B
.
【第12题解析】根据三视图可知,四棱锥的底面是边长为1的正方形、高是1,半球的半径为,所以该几何体的体积为×1×1×1+×π()3=+π.
故选C
.
填空题答案
第13题
16
第14题
5
第15题
11
第16题
(1,+∞)
【第16题解析】由三视图可知该组合几何体下面是一个圆柱,上面是一个三棱柱,故所求体积为V=×3×4×6+16π×8=36+128π.
故填36+128π.
【第17题答案】
cm
【第17题解析】如图,设圆锥母线长为l,则=,所以l=
cm.
【第18题答案】
cm3
【第18题解析】如图,连接AC、BD相交于点O,连接VO,
∵AB=BC=2
cm,
在正方形ABCD中,
求得CO=
cm,
又在直角三角形VOC中,
求得VO=
cm,
∴VV-ABCD=SABCD·VO=×4×=(cm3).
故这个四棱锥的体积为
cm3.
【第20题答案】
.
【第20题解析】由三视图可知,该几何体是大圆柱内挖掉了小圆柱,两个圆柱高均为1,底面是半径为2和的同心圆,故该几何体的体积为4π×1-π()2×1=.
【第21题答案】1:2:3.
【第21题解析】设圆柱的底面半径为r,高为h,则V圆柱=πr2h.
由题意知圆锥的底面半径为r,高为h,球的半径为r,
∴V圆锥=πr2h,
∴V球=πr3.
又h=2r,
∴V圆锥:V球:V圆柱=(πr2h):(πr3):(πr2h)=(πr3):(πr3):(2πr3)=1:2:3.
