第29讲:选修2-2第三章《数系的扩充与复数的引入》单元检测题-高中数学单元检测题 Word版含解析
文档属性
| 名称 | 第29讲:选修2-2第三章《数系的扩充与复数的引入》单元检测题-高中数学单元检测题 Word版含解析 |  | |
| 格式 | zip | ||
| 文件大小 | 329.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-08 20:50:02 | ||
图片预览


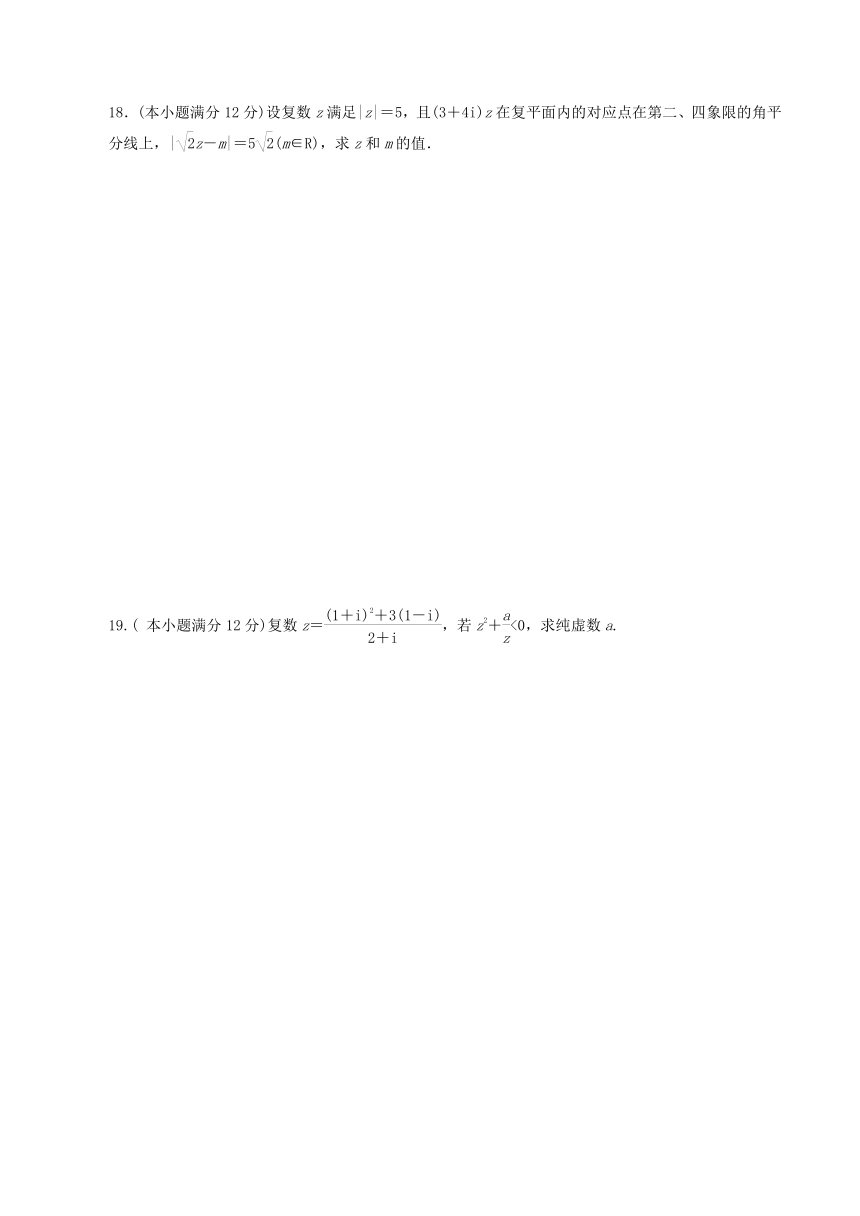

文档简介
选修2-2第三章《数系的扩充与复数的引入》单元检测题
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数z=1+cos α+isin α (π<α<2π)的模为( )
A.2cos B.-2cos
C.2sin D.-2sin
2.已知M={1,2,m2-3m-1+(m2-5m-6)i},N={-1,3},M∩N={3},则实数m的
值为( )
A.-1或6 B.-1或4
C.-1 D.4
3.若θ∈,则复数(cos θ+sin θ)+(sin θ-cos θ)i在复平面内所对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.一元二次方程x2-(5+i)x+4-i=0有一个实根x0,则( )
A.x0=4 B.x0=1
C.x0=4或x0=1 D.x0不存在
5.在复平面内,复数1+i与1+3i分别对应向量和,其中O为坐标原点,则||
等于( )
A. B.2 C. D.4
6.已知复数z= ,是z的共轭复数,则z·等于( )
A. B. C.1 D.2
7.在复平面上复数-1+i、0、3+2i所对应的点分别是A、B、C,则平行四边形ABCD
的对角线BD的长为( )
A.5 B. C. D.
8.已知复数z对应的点在第二象限,它的模是3,实部是-,则z为( )
A.-+2i B.--2i
C.+2i D.-2i
9.1+2i+3i2+…+2 005i2 004的值是( )
A.-1 000-1 000i B.-1 002-1 002i
C.1 003-1 002i D.1 005-1 000i
10.设复数z满足=i,则|1+z|等于( )
A.0 B.1 C. D.2
11.若z1=(2x-1)+yi与z2=3x+i (x,y∈R)互为共轭复数,则z1对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
12.f(n)=in+i-n (n∈N+)的值域中的元素个数是( )
A.2 B.3 C.4 D.无穷多个
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.z1是复数,z2=z1-i1(其中1表示z1的共轭复数),已知z2的实部是-1,则z2
的虚部为______.
14.如果一个复数与它的模的和为5+i,那么这个复数是________.
15.若复数z=,则|+3i|=________.
16.已知复数z1=2+3i,z2=a+bi,z3=1-4i,它们在复平面上所对应的点分别为A、
B、C.若=2+,则a=________,b=________.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知复数z=(2+i)m2--2(1-i),当实数m取什么值时,复数z是(1)虚数,(2)纯虚数.
18.(本小题满分12分)设复数z满足|z|=5,且(3+4i)z在复平面内的对应点在第二、四象限的角平分线上,|z-m|=5(m∈R),求z和m的值.
19.( 本小题满分12分)复数z=,若z2+<0,求纯虚数a.
20.(本小题满分12分)已知复数z的模为2,求复数1+i+z的模的最大值、最小值.
21.( 本小题满分12分)已知z是虚数,证明:z+为实数的充要条件是|z|=1.
22.(本小题满分12分)复数z=且|z|=4,z对应的点在第一象限,若复数0,z,对应的点是正三角形的三个顶点,求实数a、b的值.
选修2-2第三章《数系的扩充与复数的引入》单元检测题参考答案
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
B
D
B
A
B
A
C
C
C
B
【第1题解析】|z|====2
∵π<α<2π,∴<<π,∴cos <0,∴2=-2cos .故选B.
【第4题解析】由已知可得x-(5+i)x0+4-i=0,∴,该方程组无解.故选D.
【第5题解析】由题意=-,∴对应的复数为(1+3i)-(1+i)=2i,∴||=2.故选B,
【第6题解析】∵z==,∴|z|===.∴z·=|z|2=.故选A.
【第7题解析】对应的复数为-1+i,对应的复数为3+2i,∵=+,∴对应的复数为(-1+i)+(3+2i)=2+3i.∴BD的长为.故选B.
【第8题解析】设z=x+yi (x,y∈R),则x=-,由|z|=3,得(-)2+y2=9,即y2=4,∴y=±2,∵复数z对应的点在第二象限,∴y=2. ∴z=-+2i.故选A.
【第9题解析】1+2i+3i2+4i3=1+2i-3-4i=-2-2i. 周期出现,原式=501×(-2-2i)+2 005i2 004=-1 002-1 002i+2 005=1 003-1 002i.故选C.
【第10题解析】由=i,得z==-i,∴|1+z|=|1-i|=.故选C.
【第11题解析】由z1,z2互为共轭复数,得解得所以z1=(2x-1)+yi=-3-i.由复数的几何意义知z1对应的点在第三象限.故选C.
【第12题解析】根据i的周期性,当n=4k (k∈N+)时,f(n)=i4k+i-4k=1+1=2,当n=4k+1 (k∈N+)时,f(n)=i4k+1+i-(4k+1)=i+=0,当n=4k+2 (k∈N+)时,f(n)=i4k+2+i-(4k+2)=-2,
当n=4k+3 (k∈N+)时,f(n)=i4k+3+i-(4k+3)=-i-=0. 故值域中元素个数为3.故选B.
填空题答案
第13题
1
第14题
+i
第15题
第16题
-3 -10
【第13题解析】设z1=a+bi,则z2=a+bi-i(a-bi)=a-b+(b-a)i,又a-b=-1,∴b-a=1. 故填1.
【第14题解析】设z=a+bi (a、b∈R),根据题意得a+bi+=5+i,
所以有,解之得,∴z=+i. 故填+i.
【第17题解析】由于m∈R,复数z可表示为
z=(2+i)m2-3m(1+i)-2(1-i)
=(2m2-3m-2)+(m2-3m+2)i,
(1)当m2-3m+2≠0,
即m≠2且m≠1时,z为虚数.
(2)当,
即m=-时,z为纯虚数.
【第18题答案】z=±,m=0,或m=2或m=-2.
【第18题解析】设z=a+bi (a,b∈R).
因为|z|=5,所以a2+b2=25.
因为(3+4i)z=(3+4i)(a+bi)
=(3a-4b)+(4a+3b)i,
又(3+4i)z在复平面内的对应点在第二、四象限的角平分线上,
所以3a-4b+4a+3b=0,得b=7a,
所以a=±,b=±,即z=±,
所以z=±(1+7i).
当z=1+7i时,有|1+7i-m|=5,
即(1-m)2+72=50,得m=0,或m=2.
当z=-(1+7i)时,
同理可得m=0,或m=-2.
∴ ∴m=4.∴a=4i.
【第20题答案】|z+1+i|min=0,|z+1+i|max=4.
【第20题解析】利用公式||z1|-|z2||≤|z1+z2|≤|z1|+|z2|.
∵|z|=2,∴||z|-|1+i||≤|z+1+i|≤|z|+|1+i|.
∴0≤|z+1+i|≤2+2,
∴|z+1+i|min=0,|z+1+i|max=4.
【第21题答案】证明见解析
【第21题解析】设z=x+yi (x,y∈R且y≠0),
则z+=x+yi+=x+yi+=x++i.
当|z|=1,即x2+y2=1时,z+=2x∈R.
当z+∈R,即y-=0时,又y≠0,
∴x2+y2=1,即|z|=1. ∴z+为实数的充要条件是|z|=1.
本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分.满分150分.考试时间120分钟.
第Ⅰ卷(选择题 共60分)
一、选择题(本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中,只有一项是符合题目要求的)
1.复数z=1+cos α+isin α (π<α<2π)的模为( )
A.2cos B.-2cos
C.2sin D.-2sin
2.已知M={1,2,m2-3m-1+(m2-5m-6)i},N={-1,3},M∩N={3},则实数m的
值为( )
A.-1或6 B.-1或4
C.-1 D.4
3.若θ∈,则复数(cos θ+sin θ)+(sin θ-cos θ)i在复平面内所对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
4.一元二次方程x2-(5+i)x+4-i=0有一个实根x0,则( )
A.x0=4 B.x0=1
C.x0=4或x0=1 D.x0不存在
5.在复平面内,复数1+i与1+3i分别对应向量和,其中O为坐标原点,则||
等于( )
A. B.2 C. D.4
6.已知复数z= ,是z的共轭复数,则z·等于( )
A. B. C.1 D.2
7.在复平面上复数-1+i、0、3+2i所对应的点分别是A、B、C,则平行四边形ABCD
的对角线BD的长为( )
A.5 B. C. D.
8.已知复数z对应的点在第二象限,它的模是3,实部是-,则z为( )
A.-+2i B.--2i
C.+2i D.-2i
9.1+2i+3i2+…+2 005i2 004的值是( )
A.-1 000-1 000i B.-1 002-1 002i
C.1 003-1 002i D.1 005-1 000i
10.设复数z满足=i,则|1+z|等于( )
A.0 B.1 C. D.2
11.若z1=(2x-1)+yi与z2=3x+i (x,y∈R)互为共轭复数,则z1对应的点在( )
A.第一象限 B.第二象限
C.第三象限 D.第四象限
12.f(n)=in+i-n (n∈N+)的值域中的元素个数是( )
A.2 B.3 C.4 D.无穷多个
第Ⅱ卷(非选择题 共90分)
二、填空题(本大题共4个小题,每小题5分,共20分,把正确答案填在题中横线上)
13.z1是复数,z2=z1-i1(其中1表示z1的共轭复数),已知z2的实部是-1,则z2
的虚部为______.
14.如果一个复数与它的模的和为5+i,那么这个复数是________.
15.若复数z=,则|+3i|=________.
16.已知复数z1=2+3i,z2=a+bi,z3=1-4i,它们在复平面上所对应的点分别为A、
B、C.若=2+,则a=________,b=________.
三、解答题(本大题共6个小题,共70分,解答应写出文字说明,证明过程或演算步骤)
17.(本小题满分10分)已知复数z=(2+i)m2--2(1-i),当实数m取什么值时,复数z是(1)虚数,(2)纯虚数.
18.(本小题满分12分)设复数z满足|z|=5,且(3+4i)z在复平面内的对应点在第二、四象限的角平分线上,|z-m|=5(m∈R),求z和m的值.
19.( 本小题满分12分)复数z=,若z2+<0,求纯虚数a.
20.(本小题满分12分)已知复数z的模为2,求复数1+i+z的模的最大值、最小值.
21.( 本小题满分12分)已知z是虚数,证明:z+为实数的充要条件是|z|=1.
22.(本小题满分12分)复数z=且|z|=4,z对应的点在第一象限,若复数0,z,对应的点是正三角形的三个顶点,求实数a、b的值.
选修2-2第三章《数系的扩充与复数的引入》单元检测题参考答案
选择题答案
题号
1
2
3
4
5
6
7
8
9
10
11
12
答案
B
C
B
D
B
A
B
A
C
C
C
B
【第1题解析】|z|====2
∵π<α<2π,∴<<π,∴cos <0,∴2=-2cos .故选B.
【第4题解析】由已知可得x-(5+i)x0+4-i=0,∴,该方程组无解.故选D.
【第5题解析】由题意=-,∴对应的复数为(1+3i)-(1+i)=2i,∴||=2.故选B,
【第6题解析】∵z==,∴|z|===.∴z·=|z|2=.故选A.
【第7题解析】对应的复数为-1+i,对应的复数为3+2i,∵=+,∴对应的复数为(-1+i)+(3+2i)=2+3i.∴BD的长为.故选B.
【第8题解析】设z=x+yi (x,y∈R),则x=-,由|z|=3,得(-)2+y2=9,即y2=4,∴y=±2,∵复数z对应的点在第二象限,∴y=2. ∴z=-+2i.故选A.
【第9题解析】1+2i+3i2+4i3=1+2i-3-4i=-2-2i. 周期出现,原式=501×(-2-2i)+2 005i2 004=-1 002-1 002i+2 005=1 003-1 002i.故选C.
【第10题解析】由=i,得z==-i,∴|1+z|=|1-i|=.故选C.
【第11题解析】由z1,z2互为共轭复数,得解得所以z1=(2x-1)+yi=-3-i.由复数的几何意义知z1对应的点在第三象限.故选C.
【第12题解析】根据i的周期性,当n=4k (k∈N+)时,f(n)=i4k+i-4k=1+1=2,当n=4k+1 (k∈N+)时,f(n)=i4k+1+i-(4k+1)=i+=0,当n=4k+2 (k∈N+)时,f(n)=i4k+2+i-(4k+2)=-2,
当n=4k+3 (k∈N+)时,f(n)=i4k+3+i-(4k+3)=-i-=0. 故值域中元素个数为3.故选B.
填空题答案
第13题
1
第14题
+i
第15题
第16题
-3 -10
【第13题解析】设z1=a+bi,则z2=a+bi-i(a-bi)=a-b+(b-a)i,又a-b=-1,∴b-a=1. 故填1.
【第14题解析】设z=a+bi (a、b∈R),根据题意得a+bi+=5+i,
所以有,解之得,∴z=+i. 故填+i.
【第17题解析】由于m∈R,复数z可表示为
z=(2+i)m2-3m(1+i)-2(1-i)
=(2m2-3m-2)+(m2-3m+2)i,
(1)当m2-3m+2≠0,
即m≠2且m≠1时,z为虚数.
(2)当,
即m=-时,z为纯虚数.
【第18题答案】z=±,m=0,或m=2或m=-2.
【第18题解析】设z=a+bi (a,b∈R).
因为|z|=5,所以a2+b2=25.
因为(3+4i)z=(3+4i)(a+bi)
=(3a-4b)+(4a+3b)i,
又(3+4i)z在复平面内的对应点在第二、四象限的角平分线上,
所以3a-4b+4a+3b=0,得b=7a,
所以a=±,b=±,即z=±,
所以z=±(1+7i).
当z=1+7i时,有|1+7i-m|=5,
即(1-m)2+72=50,得m=0,或m=2.
当z=-(1+7i)时,
同理可得m=0,或m=-2.
∴ ∴m=4.∴a=4i.
【第20题答案】|z+1+i|min=0,|z+1+i|max=4.
【第20题解析】利用公式||z1|-|z2||≤|z1+z2|≤|z1|+|z2|.
∵|z|=2,∴||z|-|1+i||≤|z+1+i|≤|z|+|1+i|.
∴0≤|z+1+i|≤2+2,
∴|z+1+i|min=0,|z+1+i|max=4.
【第21题答案】证明见解析
【第21题解析】设z=x+yi (x,y∈R且y≠0),
则z+=x+yi+=x+yi+=x++i.
当|z|=1,即x2+y2=1时,z+=2x∈R.
当z+∈R,即y-=0时,又y≠0,
∴x2+y2=1,即|z|=1. ∴z+为实数的充要条件是|z|=1.
