2.5 一元一次不等式与一次函数同步练习
文档属性
| 名称 | 2.5 一元一次不等式与一次函数同步练习 |  | |
| 格式 | docx | ||
| 文件大小 | 362.6KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-09 16:29:12 | ||
图片预览


文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
2.5一元一次不等式与一次函数同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
1.一次函数与一元一次不等式的关系
从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;
从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
2.用画函数图象的方法解不等式kx+b>0(或<0)
对应一次函数y=kx+b,它与x轴交点为(-,0).
当k>0时,不等式kx+b>0的解为:x> ,不等式kx+b<0的解为:x< ;
当k<0,不等式kx+b>0的解为:x< ,不等式kx+b<0的解为:x>
基础知识和能力拓展训练
一、选择题
1.一次函数的图象如图所示,当时,x的取值范围是( )
A. B. C. D.
2.若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
A. x<2 B. x>2 C. x>-1 D. x<-1
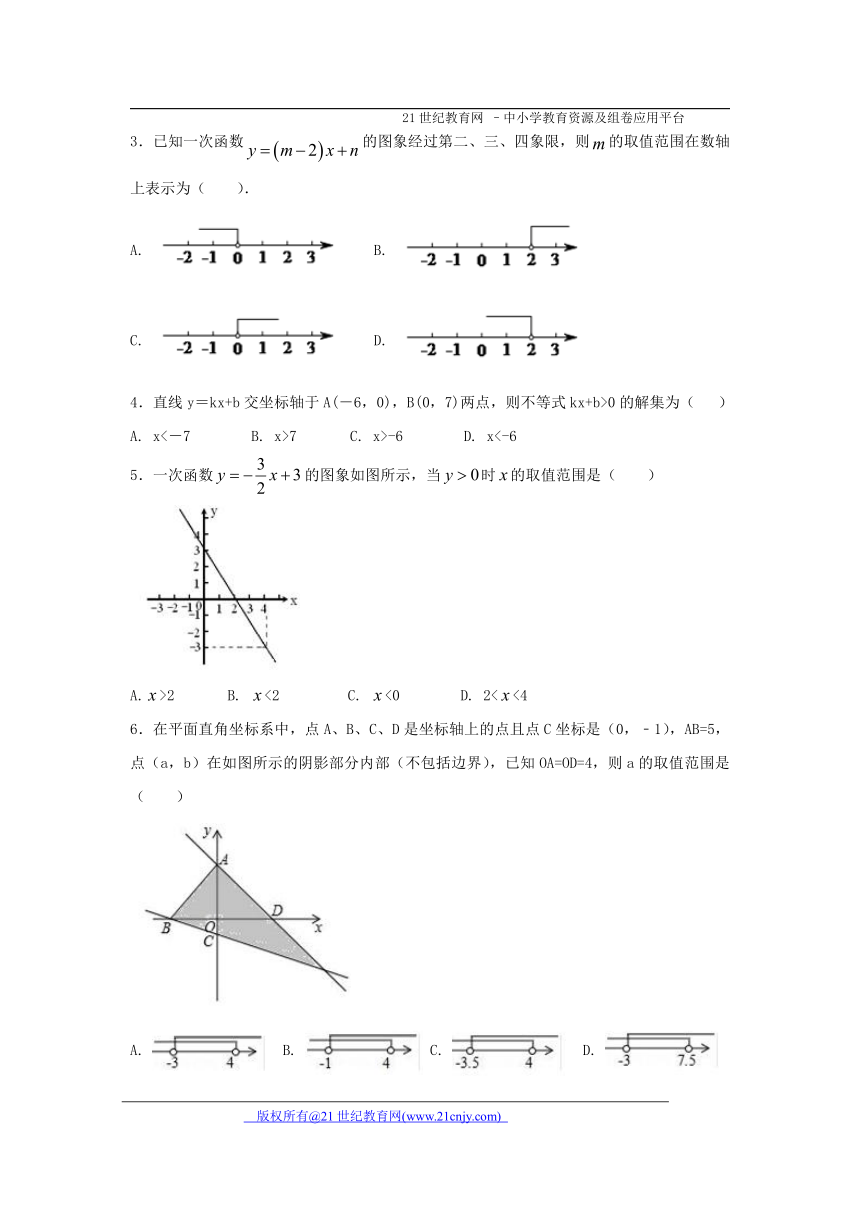
3.已知一次函数的图象经过第二、三、四象限,则的取值范围在数轴上表示为( ).
A. B.
C. D.
4.直线y=kx+b交坐标轴于A(-6,0),B(0,7)两点,则不等式kx+b>0的解集为( )
A. x<-7 B. x>7 C. x>-6 D. x<-6
5.一次函数的图象如图所示,当时的取值范围是( )
A.>2 B. <2 C. <0 D. 2<<4
6.在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,﹣1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( )
A. B. C. D.
二、填空题
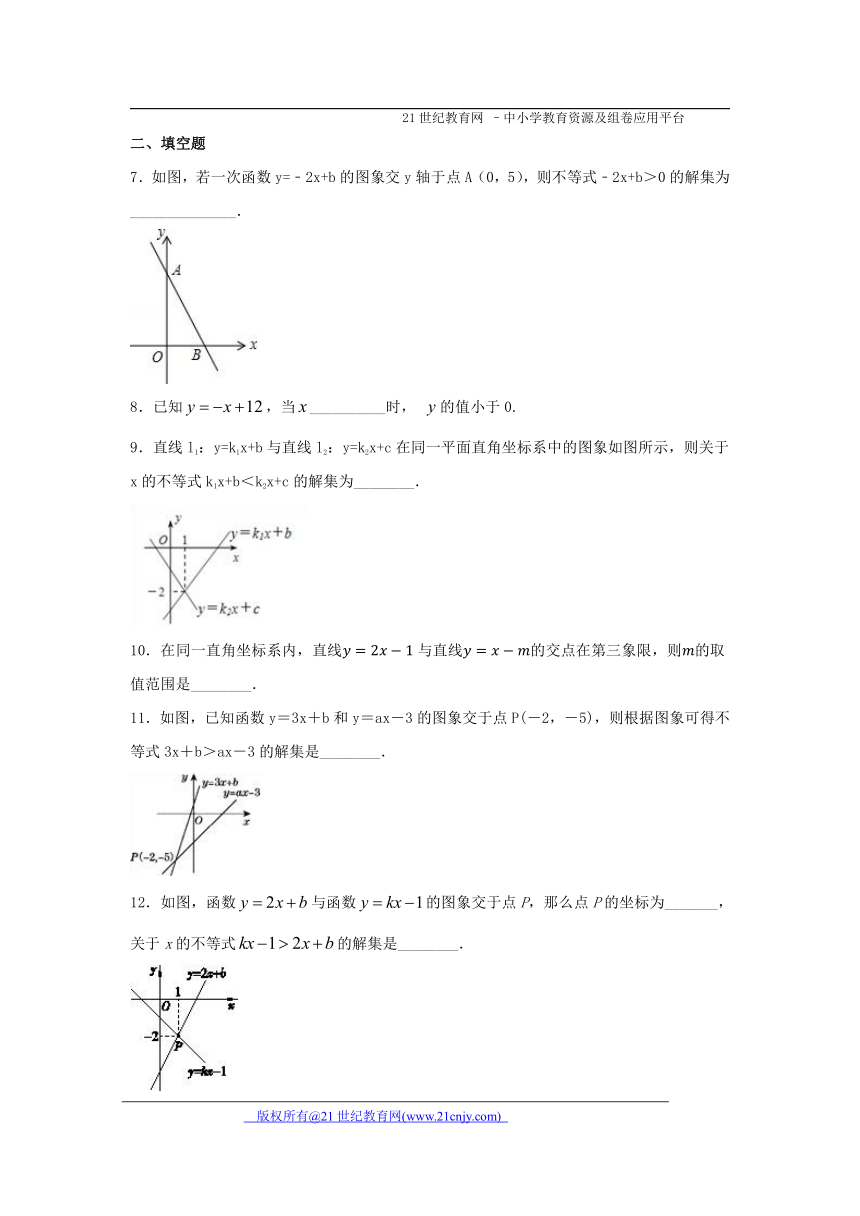
7.如图,若一次函数y=﹣2x+b的图象交y轴于点A(0,5),则不等式﹣2x+b>0的解集为______________.
8.已知,当__________时, 的值小于0.
9.直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b<k2x+c的解集为________.
10.在同一直角坐标系内,直线与直线的交点在第三象限,则的取
值范围是________.
11.如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是________.
12.如图,函数与函数的图象交于点P,那么点P的坐标为_______,关于x的不等式的解集是________.
13.已知一次函数的图象过点和点. 若,则x的取值范围是___.
14.一次函数与的图象如图所示,则当________时, .
15.已知一次函数y=kx+b的图象如图,则y>1时x的取值范围是_________.
16.如图,函数y=2x和y=ax+6的图像相交于点A(m,4),则不等式ax+6>2x的解集为________.
三、解答题
17.直线y=kx+4经过点(1,2),求不等式kx+4≥0的解集.
18.已知x2+ax+3=(x-1)(x-b),试求直线y=2x-a与直线y=bx+3的交点坐标,并直接写出关于x的不等式2x-a≥bx+3的解集。
19.已知一次函数它的图像与轴、轴分别交于A、B两点。
(1)求出点A、B的坐标,并画出这个一次函数的图像;
(2)根据图像回答:①当取何值时, >0?
②当<5时,求的取值范围。
20.如图,直线l: 与x轴、y轴分别交于点A、B,点P1(2,1)在直线l上,将点P1先向右平移1个单位,再向上平移2个单位得到像点P2.
(1)判断点P2是否在直线l上;并说明理由.
(2)若直线l上的点在x轴上方,直接写出x的取值范围.
(3)若点P为过原点O与直线l平行的直线上任意一点,直接写出S△PAB的值.
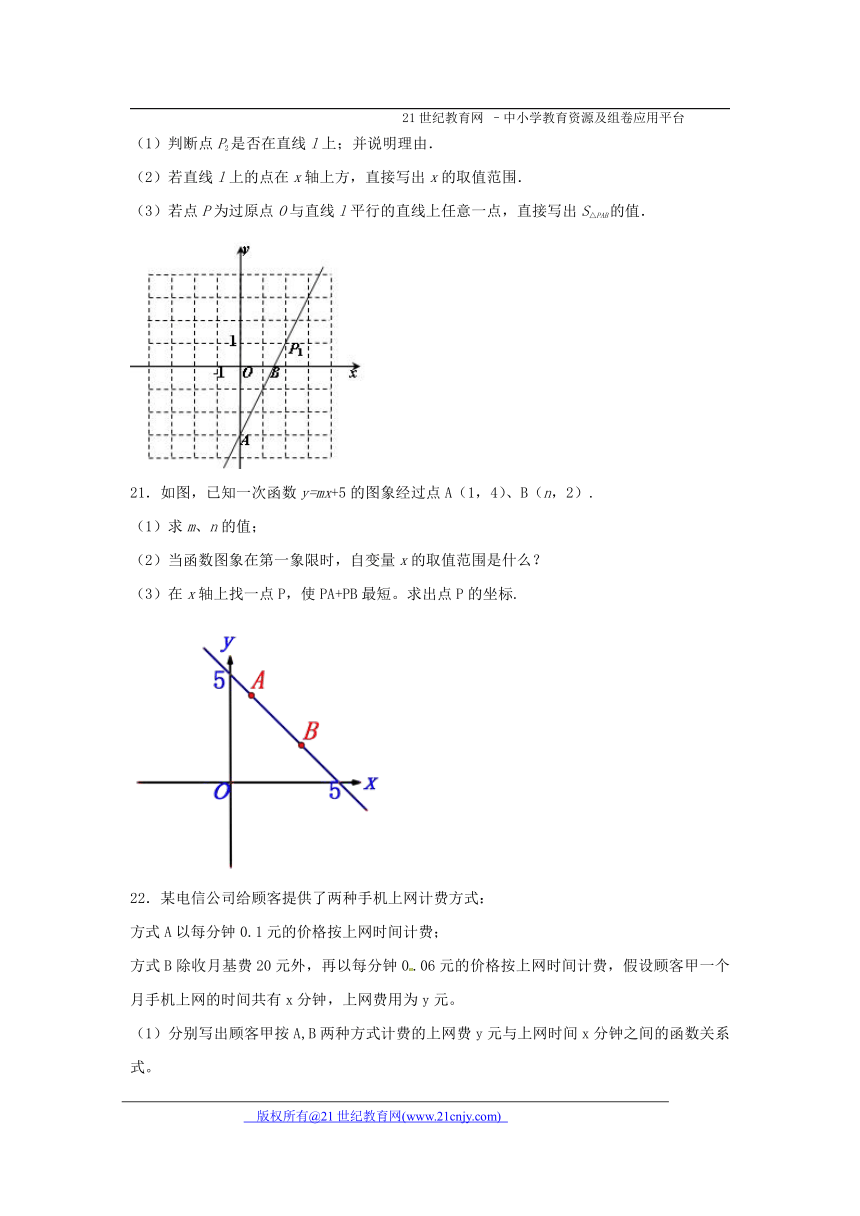
21.如图,已知一次函数y=mx+5的图象经过点A(1,4)、B(n,2).
(1)求m、n的值;
(2)当函数图象在第一象限时,自变量x的取值范围是什么?
(3)在x轴上找一点P,使PA+PB最短。求出点P的坐标.
22.某电信公司给顾客提供了两种手机上网计费方式:
方式A以每分钟0.1元的价格按上网时间计费;
方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费,假设顾客甲一个月手机上网的时间共有x分钟,上网费用为y元。
(1)分别写出顾客甲按A,B两种方式计费的上网费y元与上网时间x分钟之间的函数关系式。
(2)如何选择计费方式能使甲上网费更合算。
23.如图,在平面直角坐标系中,存在直线y1=2x和直线y2=-x+3
(1) 直接写出直线y2=-x+3与坐标轴的交点坐标:__________、__________
(2) 求出直线y1=2x和直线y2=-x+3的交点坐标
(3) 结合图象,直接写出0<y2<y1的解集:_________________
参考答案
1.A
【解析】由图像可知, 当时,x的取值范围是.
故选A.
2.C
【解析】试题解析:把(2,0)代入y=kx+b得2k+b=0,则b=-2k,
所以k(x+3)+b<0化为k(x+3)-2k<0,
即kx+k<0,
因为k<0,
所以x>-1.
故选C.
点睛:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
3.C
【解析】试题解析:因为的解析式是,为一函数表达式,且直线经过第二、三、四象限,所以根据一次函数的性质,可得, ,即, ;根据数轴的基本概念可知, 项符合题意.
故选.
4.C
【解析】由题意得, 不等式kx+b>0的解集是x>-6.
故选C.
5.B
【解析】试题解析:由函数的图象可知,当y=0时,x=2,当y>0时,x<2.
故选B.
6.D
【解析】试题解析:∵AB=5,OA=4,
∴OB=,
∴点B(-3,0).
∵OA=OD=4,
∴点A(0,4),点D(4,0).
设直线AD的解析式为y=kx+b,
将A(0,4)、D(4,0)代入y=kx+b,
,解得:,
∴直线AD的解析式为y=-x+4;
设直线BC的解析式为y=mx+n,
将B(-3,0)、C(0,-1)代入y=mx+n,
,解得:,
∴直线BC的解析式为y=-x-1.
联立直线AD、BC的解析式成方程组,
,解得:,
∴直线AD、BC的交点坐标为(,-).
∵点(a,b)在如图所示的阴影部分内部(不包括边界),
∴-3<a<.
故选D.
7.x<
【解析】∵一次函数y=﹣2x+b的图象交y轴于点A(0,5),
∴b=5,
∴一次函数y=-2x+5,
∴-2x+5>0,
∴x<
故答案是:x<.
8.x>12
【解析】试题解析:∵y<0
∴-x+12<0
∴x>12.
9.x<1
【解析】根据一次函数与不等式的关系可得: k1x+b<k2x+c表示直线l1在直线l2的下方,所以根据图象可得: x<1,故答案为: x<1.
10.m<-1
【解析】试题解析:∵,
∴解方程组得:,
∵直线y=2x-1和直线y=m-x的交点在第三象限,
∴x<0,y<0,
∴m<-1,m<0.5,
∴m<-1.
11.x>-2
【解析】试题解析:从图象得到,当x>-2时,y=3x+b的图象对应的点在函数y=ax-3的图象上面,
∴不等式3x+b>ax-3的解集为:x>-2.
12. x<1
【解析】由图像可得点P的坐标为(1,-2);不等式的解集是x<1
13.
【解析】∵一次函数的图象过点(-1,0)和点,
∴图形经过一、二、三象限,且y随x的增大而增大,
∴若,则x的取值范围是.
14.
【解析】当x>1时,y1故答案为>1.
15.x<0
【解析】由图像可知,当x<0时,y>1,
∴y>1时x的取值范围是:x<0.
16.x<2
【解析】由函数y=2x经过点A(m,4),则2m=4,解得m=2,
则点A(2,4),
不等式ax+6>2x对应的即图象上一次函数y=2x在一次函数y=ax+6下方时对应的x的值,
此时x<2.
故答案为x<2.
17.x≤2
【解析】试题分析:把点(1,2)的坐标代入直线解析式求出k值,从而得到直线解析式y=-2x+4,然后解不等式-2x+4≥0即可.
试题解析:把点(1,2)的坐标代入直线解析式y=kx+4中,
得k+4=2,
解得:k=﹣2,
则直线的函数解析式为:y=﹣2x+4,
由﹣2x+4≥0,得:x≤2.
18.x≤1
【解析】试题分析:根据x2+ax+3=(x-1)(x-b)求出a、b的值,再求出直线y=2x-a与直线y=bx+3的交点坐标,并写出直线y=2x-a的图像在直线y=bx+3的图像上方时自变量x的取值范围即可;
试题解析:
由x2+ax+3=(x-1)(x-b)=x2-(b+1)x+b
得,b=3,a=-(b+1),
a=-4,b=3
交点坐标为(1,6),
不等式的解集为x≤1.
19.(1); 图象见解析;(2)①②<5
【解析】(1); (4分) 图略
(2)当时, >0 ;当<5时,
20.(1)点P2在直线l上(2)x>;(3).
【解析】(1)∵直线l:y=mx-3,过点P1(2,1),
∴把点P1(2,1)代入y=mx-3,得1=2m-3,
∴ m=2;
y=2x-3,
由题意得P2(3,3),
∵2×3-3=3,∴点P2在直线l上,
(2)x>;
(3).
21.(1)m、 n的值分别是-1、3(2)0<x<5 (3)P(,0)
【解析】(1)将A(1,4)代入y= mx+5得:
4=m+5
解得:m= -1
∴y= -x+5
将B(n,2)代入y= -x+5得:
2= -n+5
解得:n=3
∴m、 n的值分别是-1、3
(2)0<x<5
(3)作点A关于x轴的对称点A′
∵A(1,4)
∴A′(1,-4)
连接A′B交x轴于点P,此时点P为所求的点
设直线A′B的解析式为y= kx+b,将A′(1,-4)、B(3,2)得:
解得:
∴直线A′B的解析式为:
当y=0时,
解得:
∴P(,0)
22.(1)方式A:y=0.1x(x≥0),方式B:y=0.06x+20(x≥0).(2)当一个月内上网时间少于500分时,选择方式A省钱;当一个月内上网时间等于500分时,选择方式A、方式B一样;当一个月内上网时间多于500分时,选择方式B省钱.
【解析】试题分析:(1)因为方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费.假设顾客甲一个月手机上网的时间共有x分钟,上网费用为y元,所以方式A:y=0.1x(x≥0),方式B:y=0.06x+20(x≥0).
(2)把两函数解析式联立,利用该方程组求出缴费一样的时间,再结合图象写出答案即可.
试题解析:(1)方式A:y=0.1x(x≥0),
方式B:y=0.06x+20(x≥0).
(2)解方程组,得,
∴两图象交于点P(500,50).
当一个月内上网时间少于500分时,选择方式A省钱;
当一个月内上网时间等于500分时,选择方式A、方式B一样;
当一个月内上网时间多于500分时,选择方式B省钱.
23.(1)(3,0)(0,3);(2)交点坐标(1,2);(3)1<x<3
【解析】试题分析:(1)令y2=-x+3中x=0求得y值即可得直线与y轴交点坐标,令y0求得x值即可得直线与x轴交点坐标;(2)由直线y1=2x和直线y2=-x+3联立得方程组,解方程组即可得两直线的交点坐标;(3)由图像可知当0<y2<y1,即在 x轴上方及直线y1下方的图象所对应的区间,结合(1)(2)可得.
试题解析:(1)令y=0,得x=3,令x=0,得y=3,所以直线和x轴交点为(3,0),和y轴交点为(0,3);
(2)由,解得,所以两直线交点坐标为(1,2);
(3)
由图象可知0<y2<y1的解集为1<x<3.
版权所有@21世纪教育网(www.21cnjy.com)
2.5一元一次不等式与一次函数同步练习
姓名:__________班级:__________学号:__________
本节应掌握和应用的知识点
1.一次函数与一元一次不等式的关系
从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;
从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
2.用画函数图象的方法解不等式kx+b>0(或<0)
对应一次函数y=kx+b,它与x轴交点为(-,0).
当k>0时,不等式kx+b>0的解为:x> ,不等式kx+b<0的解为:x< ;
当k<0,不等式kx+b>0的解为:x< ,不等式kx+b<0的解为:x>
基础知识和能力拓展训练
一、选择题
1.一次函数的图象如图所示,当时,x的取值范围是( )
A. B. C. D.
2.若函数y=kx+b的图象如图所示,则关于x的不等式k(x+3)+b<0的解集为( )
A. x<2 B. x>2 C. x>-1 D. x<-1
3.已知一次函数的图象经过第二、三、四象限,则的取值范围在数轴上表示为( ).
A. B.
C. D.
4.直线y=kx+b交坐标轴于A(-6,0),B(0,7)两点,则不等式kx+b>0的解集为( )
A. x<-7 B. x>7 C. x>-6 D. x<-6
5.一次函数的图象如图所示,当时的取值范围是( )
A.>2 B. <2 C. <0 D. 2<<4
6.在平面直角坐标系中,点A、B、C、D是坐标轴上的点且点C坐标是(0,﹣1),AB=5,点(a,b)在如图所示的阴影部分内部(不包括边界),已知OA=OD=4,则a的取值范围是( )
A. B. C. D.
二、填空题
7.如图,若一次函数y=﹣2x+b的图象交y轴于点A(0,5),则不等式﹣2x+b>0的解集为______________.
8.已知,当__________时, 的值小于0.
9.直线l1:y=k1x+b与直线l2:y=k2x+c在同一平面直角坐标系中的图象如图所示,则关于x的不等式k1x+b<k2x+c的解集为________.
10.在同一直角坐标系内,直线与直线的交点在第三象限,则的取
值范围是________.
11.如图,已知函数y=3x+b和y=ax-3的图象交于点P(-2,-5),则根据图象可得不等式3x+b>ax-3的解集是________.
12.如图,函数与函数的图象交于点P,那么点P的坐标为_______,关于x的不等式的解集是________.
13.已知一次函数的图象过点和点. 若,则x的取值范围是___.
14.一次函数与的图象如图所示,则当________时, .
15.已知一次函数y=kx+b的图象如图,则y>1时x的取值范围是_________.
16.如图,函数y=2x和y=ax+6的图像相交于点A(m,4),则不等式ax+6>2x的解集为________.
三、解答题
17.直线y=kx+4经过点(1,2),求不等式kx+4≥0的解集.
18.已知x2+ax+3=(x-1)(x-b),试求直线y=2x-a与直线y=bx+3的交点坐标,并直接写出关于x的不等式2x-a≥bx+3的解集。
19.已知一次函数它的图像与轴、轴分别交于A、B两点。
(1)求出点A、B的坐标,并画出这个一次函数的图像;
(2)根据图像回答:①当取何值时, >0?
②当<5时,求的取值范围。
20.如图,直线l: 与x轴、y轴分别交于点A、B,点P1(2,1)在直线l上,将点P1先向右平移1个单位,再向上平移2个单位得到像点P2.
(1)判断点P2是否在直线l上;并说明理由.
(2)若直线l上的点在x轴上方,直接写出x的取值范围.
(3)若点P为过原点O与直线l平行的直线上任意一点,直接写出S△PAB的值.
21.如图,已知一次函数y=mx+5的图象经过点A(1,4)、B(n,2).
(1)求m、n的值;
(2)当函数图象在第一象限时,自变量x的取值范围是什么?
(3)在x轴上找一点P,使PA+PB最短。求出点P的坐标.
22.某电信公司给顾客提供了两种手机上网计费方式:
方式A以每分钟0.1元的价格按上网时间计费;
方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费,假设顾客甲一个月手机上网的时间共有x分钟,上网费用为y元。
(1)分别写出顾客甲按A,B两种方式计费的上网费y元与上网时间x分钟之间的函数关系式。
(2)如何选择计费方式能使甲上网费更合算。
23.如图,在平面直角坐标系中,存在直线y1=2x和直线y2=-x+3
(1) 直接写出直线y2=-x+3与坐标轴的交点坐标:__________、__________
(2) 求出直线y1=2x和直线y2=-x+3的交点坐标
(3) 结合图象,直接写出0<y2<y1的解集:_________________
参考答案
1.A
【解析】由图像可知, 当时,x的取值范围是.
故选A.
2.C
【解析】试题解析:把(2,0)代入y=kx+b得2k+b=0,则b=-2k,
所以k(x+3)+b<0化为k(x+3)-2k<0,
即kx+k<0,
因为k<0,
所以x>-1.
故选C.
点睛:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.
3.C
【解析】试题解析:因为的解析式是,为一函数表达式,且直线经过第二、三、四象限,所以根据一次函数的性质,可得, ,即, ;根据数轴的基本概念可知, 项符合题意.
故选.
4.C
【解析】由题意得, 不等式kx+b>0的解集是x>-6.
故选C.
5.B
【解析】试题解析:由函数的图象可知,当y=0时,x=2,当y>0时,x<2.
故选B.
6.D
【解析】试题解析:∵AB=5,OA=4,
∴OB=,
∴点B(-3,0).
∵OA=OD=4,
∴点A(0,4),点D(4,0).
设直线AD的解析式为y=kx+b,
将A(0,4)、D(4,0)代入y=kx+b,
,解得:,
∴直线AD的解析式为y=-x+4;
设直线BC的解析式为y=mx+n,
将B(-3,0)、C(0,-1)代入y=mx+n,
,解得:,
∴直线BC的解析式为y=-x-1.
联立直线AD、BC的解析式成方程组,
,解得:,
∴直线AD、BC的交点坐标为(,-).
∵点(a,b)在如图所示的阴影部分内部(不包括边界),
∴-3<a<.
故选D.
7.x<
【解析】∵一次函数y=﹣2x+b的图象交y轴于点A(0,5),
∴b=5,
∴一次函数y=-2x+5,
∴-2x+5>0,
∴x<
故答案是:x<.
8.x>12
【解析】试题解析:∵y<0
∴-x+12<0
∴x>12.
9.x<1
【解析】根据一次函数与不等式的关系可得: k1x+b<k2x+c表示直线l1在直线l2的下方,所以根据图象可得: x<1,故答案为: x<1.
10.m<-1
【解析】试题解析:∵,
∴解方程组得:,
∵直线y=2x-1和直线y=m-x的交点在第三象限,
∴x<0,y<0,
∴m<-1,m<0.5,
∴m<-1.
11.x>-2
【解析】试题解析:从图象得到,当x>-2时,y=3x+b的图象对应的点在函数y=ax-3的图象上面,
∴不等式3x+b>ax-3的解集为:x>-2.
12. x<1
【解析】由图像可得点P的坐标为(1,-2);不等式的解集是x<1
13.
【解析】∵一次函数的图象过点(-1,0)和点,
∴图形经过一、二、三象限,且y随x的增大而增大,
∴若,则x的取值范围是.
14.
【解析】当x>1时,y1
15.x<0
【解析】由图像可知,当x<0时,y>1,
∴y>1时x的取值范围是:x<0.
16.x<2
【解析】由函数y=2x经过点A(m,4),则2m=4,解得m=2,
则点A(2,4),
不等式ax+6>2x对应的即图象上一次函数y=2x在一次函数y=ax+6下方时对应的x的值,
此时x<2.
故答案为x<2.
17.x≤2
【解析】试题分析:把点(1,2)的坐标代入直线解析式求出k值,从而得到直线解析式y=-2x+4,然后解不等式-2x+4≥0即可.
试题解析:把点(1,2)的坐标代入直线解析式y=kx+4中,
得k+4=2,
解得:k=﹣2,
则直线的函数解析式为:y=﹣2x+4,
由﹣2x+4≥0,得:x≤2.
18.x≤1
【解析】试题分析:根据x2+ax+3=(x-1)(x-b)求出a、b的值,再求出直线y=2x-a与直线y=bx+3的交点坐标,并写出直线y=2x-a的图像在直线y=bx+3的图像上方时自变量x的取值范围即可;
试题解析:
由x2+ax+3=(x-1)(x-b)=x2-(b+1)x+b
得,b=3,a=-(b+1),
a=-4,b=3
交点坐标为(1,6),
不等式的解集为x≤1.
19.(1); 图象见解析;(2)①②<5
【解析】(1); (4分) 图略
(2)当时, >0 ;当<5时,
20.(1)点P2在直线l上(2)x>;(3).
【解析】(1)∵直线l:y=mx-3,过点P1(2,1),
∴把点P1(2,1)代入y=mx-3,得1=2m-3,
∴ m=2;
y=2x-3,
由题意得P2(3,3),
∵2×3-3=3,∴点P2在直线l上,
(2)x>;
(3).
21.(1)m、 n的值分别是-1、3(2)0<x<5 (3)P(,0)
【解析】(1)将A(1,4)代入y= mx+5得:
4=m+5
解得:m= -1
∴y= -x+5
将B(n,2)代入y= -x+5得:
2= -n+5
解得:n=3
∴m、 n的值分别是-1、3
(2)0<x<5
(3)作点A关于x轴的对称点A′
∵A(1,4)
∴A′(1,-4)
连接A′B交x轴于点P,此时点P为所求的点
设直线A′B的解析式为y= kx+b,将A′(1,-4)、B(3,2)得:
解得:
∴直线A′B的解析式为:
当y=0时,
解得:
∴P(,0)
22.(1)方式A:y=0.1x(x≥0),方式B:y=0.06x+20(x≥0).(2)当一个月内上网时间少于500分时,选择方式A省钱;当一个月内上网时间等于500分时,选择方式A、方式B一样;当一个月内上网时间多于500分时,选择方式B省钱.
【解析】试题分析:(1)因为方式A以每分钟0.1元的价格按上网时间计费;方式B除收月基费20元外,再以每分钟0.06元的价格按上网时间计费.假设顾客甲一个月手机上网的时间共有x分钟,上网费用为y元,所以方式A:y=0.1x(x≥0),方式B:y=0.06x+20(x≥0).
(2)把两函数解析式联立,利用该方程组求出缴费一样的时间,再结合图象写出答案即可.
试题解析:(1)方式A:y=0.1x(x≥0),
方式B:y=0.06x+20(x≥0).
(2)解方程组,得,
∴两图象交于点P(500,50).
当一个月内上网时间少于500分时,选择方式A省钱;
当一个月内上网时间等于500分时,选择方式A、方式B一样;
当一个月内上网时间多于500分时,选择方式B省钱.
23.(1)(3,0)(0,3);(2)交点坐标(1,2);(3)1<x<3
【解析】试题分析:(1)令y2=-x+3中x=0求得y值即可得直线与y轴交点坐标,令y0求得x值即可得直线与x轴交点坐标;(2)由直线y1=2x和直线y2=-x+3联立得方程组,解方程组即可得两直线的交点坐标;(3)由图像可知当0<y2<y1,即在 x轴上方及直线y1下方的图象所对应的区间,结合(1)(2)可得.
试题解析:(1)令y=0,得x=3,令x=0,得y=3,所以直线和x轴交点为(3,0),和y轴交点为(0,3);
(2)由,解得,所以两直线交点坐标为(1,2);
(3)
由图象可知0<y2<y1的解集为1<x<3.
版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第一章 三角形的证明
- 1 等腰三角形
- 2 直角三角形
- 3 线段的垂直平分线
- 4 角平分线
- 第二章 一元一次不等式和一元一次不等式组
- 1 不等关系
- 2 不等式的基本性质
- 3 不等式的解集
- 4 一元一次不等式
- 5 一元一次不等式与一次函数
- 6 一元一次不等式组
- 第三章 图形的平移与旋转
- 1 图形的平移
- 2 图形的旋转
- 3 中心对称
- 4 简单的图案设计
- 第四章 因式分解
- 1 因式分解
- 2 提公因式法
- 3 公式法
- 第五章 分式与分式方程
- 1 认识分式
- 2 分式的乘除法
- 3 分式的加减法
- 4 分式方程
- 第六章 平行四边形
- 1 平行四边形的性质
- 2 平行四边形的判定
- 3 三角形的中位线
- 4 多边形的内角与外角和
