21.2一次函数的图像和性质 课件

课件35张PPT。一次函数的图像和性质（1）1.经历作图过程，初步了解作函数图像的一般步骤；
2.理解一次函数的代数表达式与图像之间的对应关系；
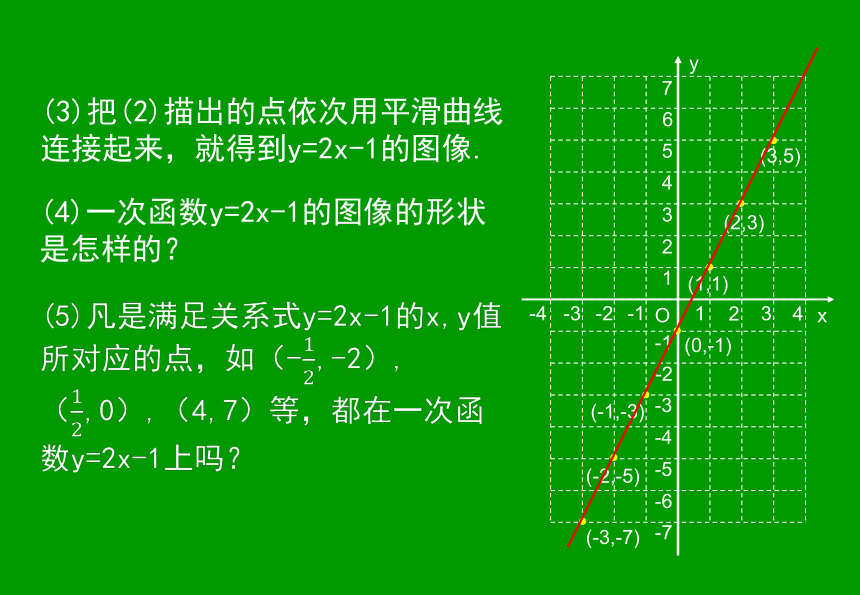
3.能较熟练作出一次函数的图像.学习目标：已知函数的表达式，通过列表、描点和连线，可以在直角坐标系中画出这个函数图像。精讲：已知一次函数y=2x-1.
(1)填写下表：(2)以(1)中得到的每对对应值分别为横坐标和纵坐标，在图中所示的直角坐标系中，描出相应的点.(3)把(2)描出的点依次用平滑曲线连接起来，就得到y=2x-1的图像.(4)一次函数y=2x-1的图像的形状是怎样的？?一般地，一次函数y=kx+b的图像为一条直线.因此，我们把一次函数y=kx+b的图像也称为直线y=kx+b.
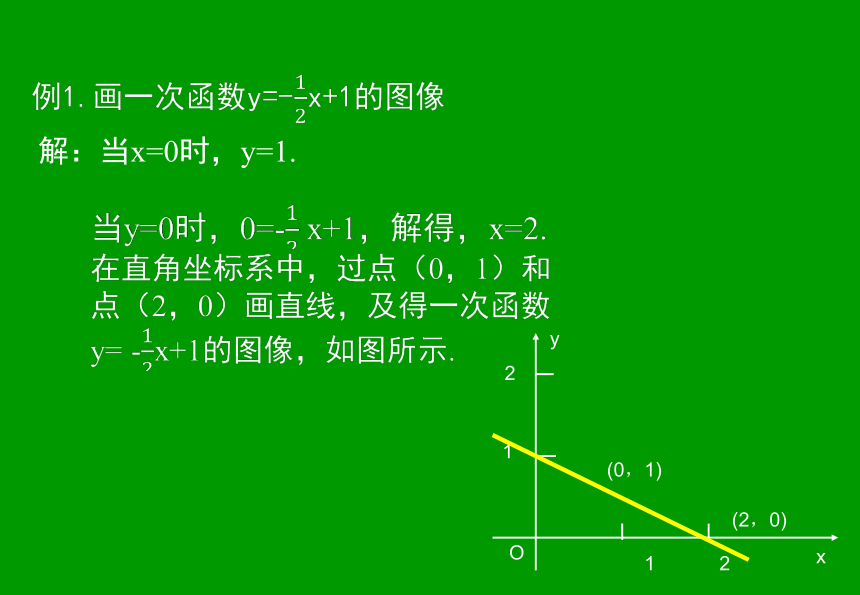
在画一次函数的图像时，只要确定出两个点，再过这两点画直线就可以了.?解：当x=0时，y=1.21(0，1)(2，0)??练习在同一直角坐标系中，画出y=x和y=1-x的图像.解析: 当x=0时，函数y=x=0；函数y=1-x=1.
当x=1时，函数y=x=1；函数y=1-x=0.
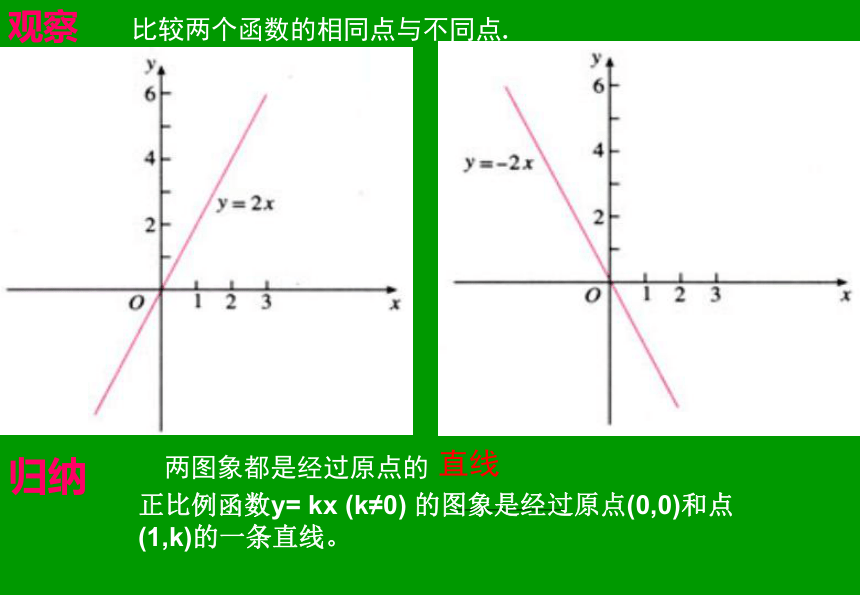
所以在坐标系中，过点(0，0)，(1，1)做直线，即可得一次函数y=x的图像；过点(0，1)，(1，0)做直线，即可得一次函数y=1-x的图像，如图：(1，1)y=xy=1-x????观察 比较两个函数的相同点与不同点.归纳 两图象都是经过原点的直线正比例函数y= kx (k≠0) 的图象是经过原点(0,0)和点(1,k)的一条直线。
典型题析：1. 填表并观察下列两个函数的变化情况.(1)在同一个直角坐标系中画出这两个函数的图像.(2)它们的图像有公共点吗？如果有，请写出公共点的坐标.yOx(0，2)(2，-8)(1，-3)(0，-10)y=x-10y=-5x+2解析:
(1) y=-5x+2的函数图像经过点(0，2)，(1，-3)，过这两点做直线，即为y=-5x+2的函数图像；
y=x-10的函数图像经过点(0，-10),
(2，-8)，过这两点做直线，即为y=-5x+2的函数图像.(2)由图可知，这两个函数图像有公共点，由表可知，其公共点坐标为(2，-8)
(或者联立这两个函数，令-5x+2=x-10，解得x=2，y=x-10=-8).2. 今有一根弹簧，不悬挂重物时的长度为12cm，悬挂的重物每增加1kg(重物不超过8kg)，弹簧的长度就增加0.5cm.写出弹簧长度y(cm)和悬挂物的质量x(kg)之间的函数关系式，指出自变量的取值范围，并画出这个函数的图像.?自变量x的取值范围为：0≤x≤8.函数图像如图：yOx1216一次函数的性质
（2）例1.已知关于x的一次函数y=(2k-1)x+(2k+1).
(1)当k满足什么条件时，函数y的值随x的值的增大而增大？
(2)当k满足什么条件时，y=(2k-1)x+(2k+1)的图像经过原点？
(3)当k满足什么条件时，函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的下方？
(4)当k满足什么条件时，函数y的值随x的值的增大而减小且函数图像与y轴的交点在x轴的上方？解析:
(1)当2k-1＞0时，y的值随x的值增大而增大.
解2k-1＞0，得：k＞0.5.
(2)当2k+1=0，即k=-0.5时，函数y=(2k-1)x+(2k+1)的图像经过原点.
(3)当2k+1＜0，函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的下方.
解2k+1＜0，得k＜-0.5.
(4)当2k-1＜0时，y的值随x的值增大而减小.解得：k ＜0.5.
当2k+1＞ 0，函数y=(2k-1)x+(2k+1)的图像与y轴的交点在x轴的上方.解得k＞ -0.5.
所以此时k的取值范围为(-0.5，0.5).练习1.判断下列函数中，y的值随x的值增大而变化的情况.(1) y=-3x+3； (2) y=3x-3；
(3) y=(3-π)x； (4) y=0.5x.解析:
(1)式中，-3＜0，所以该函数y的值随x的值增大而减小；
(2)式中，3＞0，所以该函数y的值随x的值增大而增大；
(3)式中，3-π＜0，所以该函数y的值随x的值增大而减小；
(4)式中，0.5＞0，所以该函数y的值随x的值增大而增大.2.已知关于x的一次函数y=kx+4k-2.
(1)如果函数的图像经过原点，求k的值.
(2)如果y的值随x的值的增大而减小，求k的取值范围.解析:
(1)该函数的图像经过原点，即其常数项为0，所以4k-2=0，解得，k=0.5.
(2)该函数y的值随x的值的增大而减小，即其自变量系数小于0，所以k＜0.3. 画出函数y=-3x+3的图像，结合图像回答下列问题：
(1) y的值随x的值增大而 （填“增大”或“减小”），图像从左到右 （填“上升”或“下降”）
(2)当y＜0时，求x的取值范围.
(3)当0＜x＜1时，求y的取值范围.yOx解析: 图像如图所示减小下降 (1)由图像可以得出答案. (2)由图可知，当y＜0时，x的取值范围为x＞1. (3)由图可知，当0＜x＜1时，y的取值范围为0＜y＜3.4.某面食加工部每周用10000元流动资金采购面粉及其他物品，其中购买面粉的质量在1500kg-2000kg之间，面粉的单价为3.6元/千克，用剩余款额y元购买其他物品.设购买面粉的质量为x kg. (1)求y与x的函数关系式，并写出自变量的取值范围. (2)画出该函数的图像. (3)观察图像，写出购买其他物品的款额y的取值范围.解析:
(1)由题意可知，购买面粉的资金为3.6x，总资金为10000元，即3.6x+y=10000，所以该函数式为:
y=-3.6x+10000，其中x的取值范围是1500≤x≤2000.(2)该函数图像如图所示：yOx1000200010002000300040005000150046002800 (3)观察图像，由图可知，该函数随x值的增大，y的值逐渐变小.所以y的值最大为y=-3.6x+10000
=10000-(-3.6*1500)=4600；最小为y=-3.6x+10000
=10000-(-3.6*2000)=2800.
y的取值范围即为:
2800≤y≤4600.( 遵义）P1(x1，y1)，P2(x2，y2)是正比例函数
y=-0.5x图象上的两点，下列判断中，正确的是( )真题链接：解析:根据正比例函数图象的性质: 当k＜0时，y随x的增大而减小，所以D为正确答案．A. y1＞y2 C.当x1＜x2时，y1＜y2 B. y1＜y2 D.当x1＜x2时，y1＞y2 D眉山）若实数a,b,c满足a+b+c=0，且a＜b＜c，则函数y=cx+a的可能是( )解析:由于a+b+c=0，且a＜b＜c，所以a＜0＜c，因为c＞0，所以y的值随x的值的增大而增大; a＜0，所以该函数与y轴的交点在y轴负半轴.观察图象可知，C为正确答案. A. B. C. D.C( 鞍山）在一次函数y=kx+2中，若y随x的增大而增大，则它的图象不经过第 象限．解析:由于y随x的增大而增大，所以k＞0，同时2＞0，所以大致图象如下图所示， 故而该函数的图象经过一、二、三象限，不经过第四象限.四归纳总结：1.一次函数y=kx+b的图像为一条直线，故其图像又称为直线y=kx+b.
2.一次函数y=kx+b中的系数k与b决定着它的性质：
(1)当k＞0时，y随x的增大而增大，图像从左向右是上升的.
(2)当k＜0时，y随x的增大而减小，图像从左向右是下降的.
(3)当b=0时，一次函数y=kx+b为正比例函数y=kx，它的图像一定经过原点.
(4)当b≠0时，直线y=kx+b一定不经过原点.例 题例1、已知函数y=(m+1)x-3
(1)当m取何值时，y随x的增大而增大？
这时它的图象经过哪些象限?
(2)当 m取何值时，y随x的增大而减小？
这时它的图象经过哪些象限?解：当m+1>0即m>-1时y随x的增大而增大，当m+1<0即m<-1时y随x的增大而减小，这时它的图象经过一、三、四象限
这时它的图象经过二、三、四象限
画出函数y=-2x+2的图象,结合图象回答下列问题：
(1)?? 这个函数中,随着x的增大,y将增大还是减小?
它的图象从左到右怎样变化?
(2)?? 当x取何值时,y=0?
当x取何值时,y＞0?
当0
做一做解： (1)因为K=-2 <0 ，所以y随x增大而减小，函数
图象从左到右下降。(2)因为 y=0 所以 -2x+2=0 ，x=1因为 当 x=0 时 y=2 , 当 x=1 时 y=0；
又因为y随x增大而减小，所以 2 ＞ y＞ 0即 0 < y<2因为 y＞0 所以 -2x+2 ＞ 0 ， x < 12、已知函数y=(m+1)x-3．
(1)当m取何值时，y随x的增大而增大？
(2)当m取何值时，y随x的增大而减小？ (1)当m+1>0即m>-1时y随x的增大而增大;(2)当m+1<0即m<-1时y随x的增大而减小. 3、若直线 y =mx+n经过第一、 二、三象限，讨论
m、n的符号.m＞0，n＞04、一次函数y=kx+b的图象如图所示，则k 0,
b 0．<<5、一次函数y=ax+b与y=ax+c(a>0)在同一坐标系中的图象可能是（　）A 6、已知点(2,m) 、(-3,n)都在直线 上，试比较 m和n的大小.你能想出几种判断的方法?
所以函数y随x增大而增大解：方法一 把两点的坐标代入函数关系式当 x=2 时, m=当 x= -3 时, n=
所以 m > n.方法二因为 k=>0，从而直接得到 m > n.例 题例2、对于一次函数y=(a+4)x+2a-1,如果
y随x的增大而增大，且它的图象与y轴的
交点在x轴的下方，试求a的取值范围解：因为y随x的增大而增大，
所以 a+4>0 即 a>-4又因为它的图象与y轴的交点在x轴的下方
所以 2a-1 < 0 即 a < 1/2所以 -4 < a < 1/21. 一次函数 的图象经过 象限。y随x的增大而 ,它的图象与x轴、y轴的坐标分别为___________________。
2．函数y=(k-1)x+2，当k＞1时，y随x的增大而______,当k＜1时，y随x的增大而_____。
一、二、四减小（2，0）增大减小小试牛刀（0，4） 画出函数y=-2x+2的图象,结合图象
回答下列问题：
(1)?? 这个函数中,随着x的增大,y将增大
还是减小?
它的图象从左到右怎样变化?
(2)?? 当x取何值时,y=0?
当x取何值时,y＞0?
当0
做一做例 题例1、已知函数y=(m+1)x-3
(1)当m取何值时，y随x的增大而增大？
这时它的图象经过哪些象限?
(2)当 m取何值时，y随x的增大而减小？
这时它的图象经过哪些象限?谢 谢