数学四年级下青岛版六三制四 认识多边形过关检测卷(含答案)
文档属性
| 名称 | 数学四年级下青岛版六三制四 认识多边形过关检测卷(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 296.3KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-10 18:56:30 | ||
图片预览


文档简介
第四单元过关检测卷
一、动脑筋想一想,填一填。(每空1分,共17分)
1.平行四边形和梯形都有( )条高,三角形有( )条高。
2.一个三角形中最少有( )个锐角,最多有( )个钝角。
3.用一根长18厘米的铁丝正好围成一个等边三角形,它的边长是( )厘米。
4.三脚架是应用了三角形的( )。
5.在直角三角形中,一个锐角是45°,另一个锐角是( )°,这也是一个( )三角形。
6.平行四边形相邻的两边长分别是5 cm和3 cm,这个平行四边形的周长是( )cm。
7.一个等腰三角形的底角是55°,顶角是( )°。
8.钝角三角形中,两个锐角的度数和( )90°。(填“大于”“小于”或“等于”)
9.图中∠1=( )°。
10.如果三角形的两边长分别是6 cm和11 cm,那么第三边最短是( )cm,最长是( )cm。(取整厘米数)
11.在一个三角形中,∠A,∠B,∠C是它的三个内角。如果∠A是∠C的2倍,∠B是∠C的3倍,那么∠A=( ),∠B=( ),∠C=( )。
二、判断对错。(每题2分,共10分)
1.钝角三角形的内角和大于锐角三角形的内角和。 ( )
2.两个完全一样的梯形可以拼成一个平行四边形。 ( )
3.有两个角是锐角的三角形,就是锐角三角形。 ( )
4.如右图,把三角形一个35°的内角剪掉,所剩图形的内角和就是145°了。 ( )
5.梯形的两底平行但不相等,两腰不平行但有可能相等。( )
三、选一选。(每题2分,共12分)
1.用同样长的三根小木棍可以围成一个( )三角形。
A.锐角 B.钝角 C.直角
2.右图中AB边对应的高是( )。
A.AD B.AE
C.CF
3.一个等腰三角形的两条边长分别是3厘米和9厘米,这个三角形的周长是( )厘米。
A.15 B.21 C.15或21
4.三角形中最小的一个角是50°,按角分类,这是一个( )三角形。
A.锐角 B.直角 C.钝角
5. 左图中有( )个三角形。
A.6 B.12 C.16
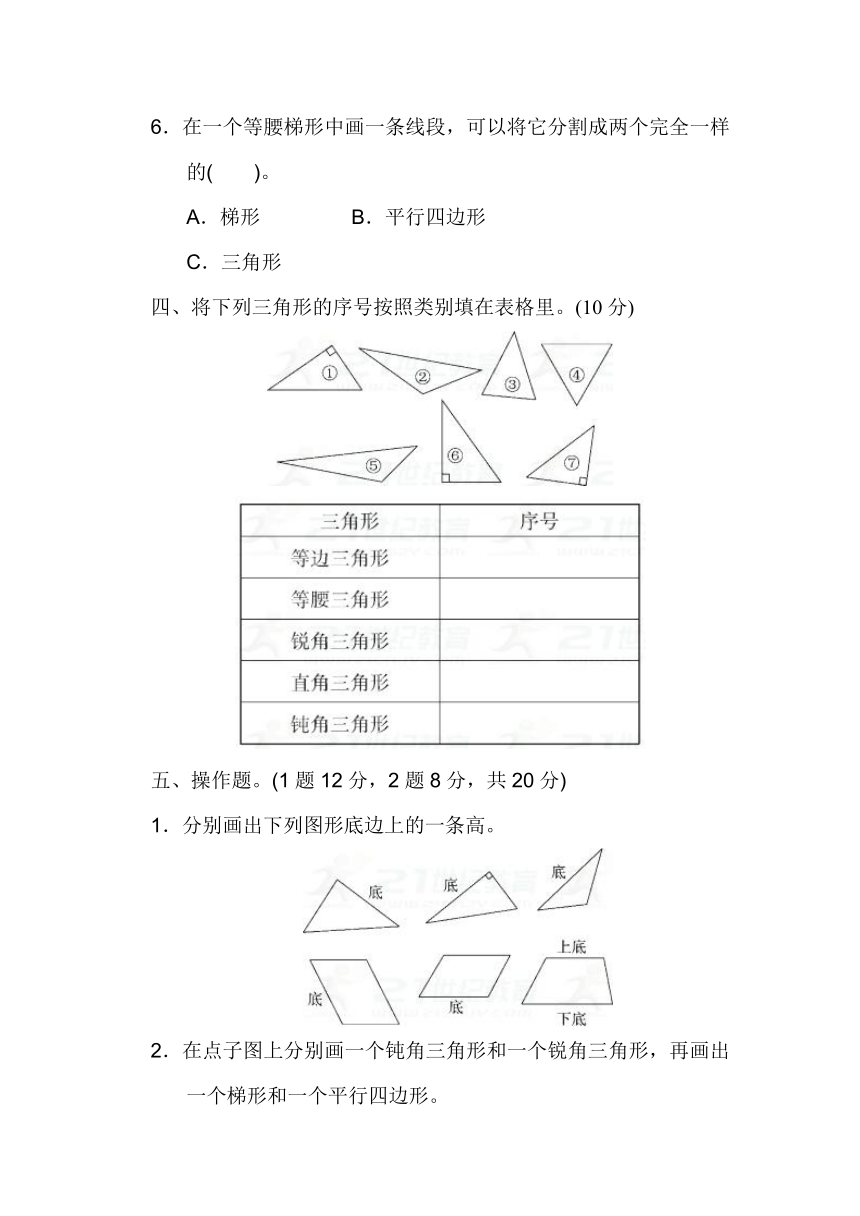
6.在一个等腰梯形中画一条线段,可以将它分割成两个完全一样的( )。
A.梯形 B.平行四边形
C.三角形
四、将下列三角形的序号按照类别填在表格里。(10分)
五、操作题。(1题12分,2题8分,共20分)
1.分别画出下列图形底边上的一条高。
2.在点子图上分别画一个钝角三角形和一个锐角三角形,再画出一个梯形和一个平行四边形。
六、解决问题。(5题6分,其余每题5分,共31分)
1.小丽用40厘米长的铁丝做了一个腰长是15厘米的等腰三角形风筝架。这个风筝架的底边长是多少厘米?
2.有一个三角形的湖(如下图),小明如果从B点出发,穿过湖到湖边AC上,沿什么路线最短?你能画出来吗?
3.一个等腰梯形中,上底是5cm,下底是上底的3倍,腰比下底少8cm,求这个梯形的周长是多少?
4.长度分别为7 cm,3 cm,4 cm,5 cm,10 cm的五根小棒共可以拼成几种不同的三角形,请都写出来。
5.在下面的三角形中,已知∠1=75°,∠2=60°,你能求出∠3和∠4的度数吗?想一想:∠4,∠1和∠2有什么关系?
6.
答案
一、1.无数 3 2.2 1 3.6 4.稳定性
5.45 等腰 6.16 7.70 8.小于
9.105 10.6 16 11.60° 90° 30°
二、1.× 2.√ 3.× 4.× 5.√
三、1.A 2.C
3.B 点拨:三角形的腰长只能是9厘米,而不能是3 厘米,因为腰长如果是3厘米,3+3<9,不能围成三角形。
4.A 5.B 6.A
四、④ ③④⑦ ③④ ①⑥⑦ ②⑤
五、1.
2.略,答案不唯一。
六、1.40-15×2=10(厘米)
答:这个风筝架的底边长是10厘米。
2.沿AC边上的高最短,如图。
3.5×3=15 (cm) 15-8=7 (cm)
5+15+7×2=34 (cm)
答:这个梯形的周长是34 cm。
4.可以拼成5种不同的三角形,三边长分别为:
①7 cm;3 cm;5 cm;②3 cm;4 cm;5 cm;
③7 cm;4 cm;5 cm;④7 cm;4 cm;10 cm;
⑤7 cm;5 cm;10 cm。
5.∠3=180°-∠1-∠2=180°-75°-60°=105°-60°=45°
∠4=180°-∠3=180°-45°=135°
∠1+∠2=75°+60°=135°,所以∠4=∠1+∠2。
点拨:根据三角形的内角和是180°列式计算,即可求出∠3的度数。根据平角是180°列式计算,即可求出∠4的度数。
6.四边形的内角和:180°×2=360°
五边形的内角和:180°×3=540°
点拨:把四边形和五边形分别分成2个三角形和3个三角形,然后根据每个三角形的内角和是180°求出四边形和五边形的内角和。
一、动脑筋想一想,填一填。(每空1分,共17分)
1.平行四边形和梯形都有( )条高,三角形有( )条高。
2.一个三角形中最少有( )个锐角,最多有( )个钝角。
3.用一根长18厘米的铁丝正好围成一个等边三角形,它的边长是( )厘米。
4.三脚架是应用了三角形的( )。
5.在直角三角形中,一个锐角是45°,另一个锐角是( )°,这也是一个( )三角形。
6.平行四边形相邻的两边长分别是5 cm和3 cm,这个平行四边形的周长是( )cm。
7.一个等腰三角形的底角是55°,顶角是( )°。
8.钝角三角形中,两个锐角的度数和( )90°。(填“大于”“小于”或“等于”)
9.图中∠1=( )°。
10.如果三角形的两边长分别是6 cm和11 cm,那么第三边最短是( )cm,最长是( )cm。(取整厘米数)
11.在一个三角形中,∠A,∠B,∠C是它的三个内角。如果∠A是∠C的2倍,∠B是∠C的3倍,那么∠A=( ),∠B=( ),∠C=( )。
二、判断对错。(每题2分,共10分)
1.钝角三角形的内角和大于锐角三角形的内角和。 ( )
2.两个完全一样的梯形可以拼成一个平行四边形。 ( )
3.有两个角是锐角的三角形,就是锐角三角形。 ( )
4.如右图,把三角形一个35°的内角剪掉,所剩图形的内角和就是145°了。 ( )
5.梯形的两底平行但不相等,两腰不平行但有可能相等。( )
三、选一选。(每题2分,共12分)
1.用同样长的三根小木棍可以围成一个( )三角形。
A.锐角 B.钝角 C.直角
2.右图中AB边对应的高是( )。
A.AD B.AE
C.CF
3.一个等腰三角形的两条边长分别是3厘米和9厘米,这个三角形的周长是( )厘米。
A.15 B.21 C.15或21
4.三角形中最小的一个角是50°,按角分类,这是一个( )三角形。
A.锐角 B.直角 C.钝角
5. 左图中有( )个三角形。
A.6 B.12 C.16
6.在一个等腰梯形中画一条线段,可以将它分割成两个完全一样的( )。
A.梯形 B.平行四边形
C.三角形
四、将下列三角形的序号按照类别填在表格里。(10分)
五、操作题。(1题12分,2题8分,共20分)
1.分别画出下列图形底边上的一条高。
2.在点子图上分别画一个钝角三角形和一个锐角三角形,再画出一个梯形和一个平行四边形。
六、解决问题。(5题6分,其余每题5分,共31分)
1.小丽用40厘米长的铁丝做了一个腰长是15厘米的等腰三角形风筝架。这个风筝架的底边长是多少厘米?
2.有一个三角形的湖(如下图),小明如果从B点出发,穿过湖到湖边AC上,沿什么路线最短?你能画出来吗?
3.一个等腰梯形中,上底是5cm,下底是上底的3倍,腰比下底少8cm,求这个梯形的周长是多少?
4.长度分别为7 cm,3 cm,4 cm,5 cm,10 cm的五根小棒共可以拼成几种不同的三角形,请都写出来。
5.在下面的三角形中,已知∠1=75°,∠2=60°,你能求出∠3和∠4的度数吗?想一想:∠4,∠1和∠2有什么关系?
6.
答案
一、1.无数 3 2.2 1 3.6 4.稳定性
5.45 等腰 6.16 7.70 8.小于
9.105 10.6 16 11.60° 90° 30°
二、1.× 2.√ 3.× 4.× 5.√
三、1.A 2.C
3.B 点拨:三角形的腰长只能是9厘米,而不能是3 厘米,因为腰长如果是3厘米,3+3<9,不能围成三角形。
4.A 5.B 6.A
四、④ ③④⑦ ③④ ①⑥⑦ ②⑤
五、1.
2.略,答案不唯一。
六、1.40-15×2=10(厘米)
答:这个风筝架的底边长是10厘米。
2.沿AC边上的高最短,如图。
3.5×3=15 (cm) 15-8=7 (cm)
5+15+7×2=34 (cm)
答:这个梯形的周长是34 cm。
4.可以拼成5种不同的三角形,三边长分别为:
①7 cm;3 cm;5 cm;②3 cm;4 cm;5 cm;
③7 cm;4 cm;5 cm;④7 cm;4 cm;10 cm;
⑤7 cm;5 cm;10 cm。
5.∠3=180°-∠1-∠2=180°-75°-60°=105°-60°=45°
∠4=180°-∠3=180°-45°=135°
∠1+∠2=75°+60°=135°,所以∠4=∠1+∠2。
点拨:根据三角形的内角和是180°列式计算,即可求出∠3的度数。根据平角是180°列式计算,即可求出∠4的度数。
6.四边形的内角和:180°×2=360°
五边形的内角和:180°×3=540°
点拨:把四边形和五边形分别分成2个三角形和3个三角形,然后根据每个三角形的内角和是180°求出四边形和五边形的内角和。
