数学六年级下苏教版7 立体图形的表面积和体积——圆柱和圆锥课件(25张)
文档属性
| 名称 | 数学六年级下苏教版7 立体图形的表面积和体积——圆柱和圆锥课件(25张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 苏教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-11 16:43:57 | ||
图片预览








文档简介
课件25张PPT。立体图形的表面积和体积
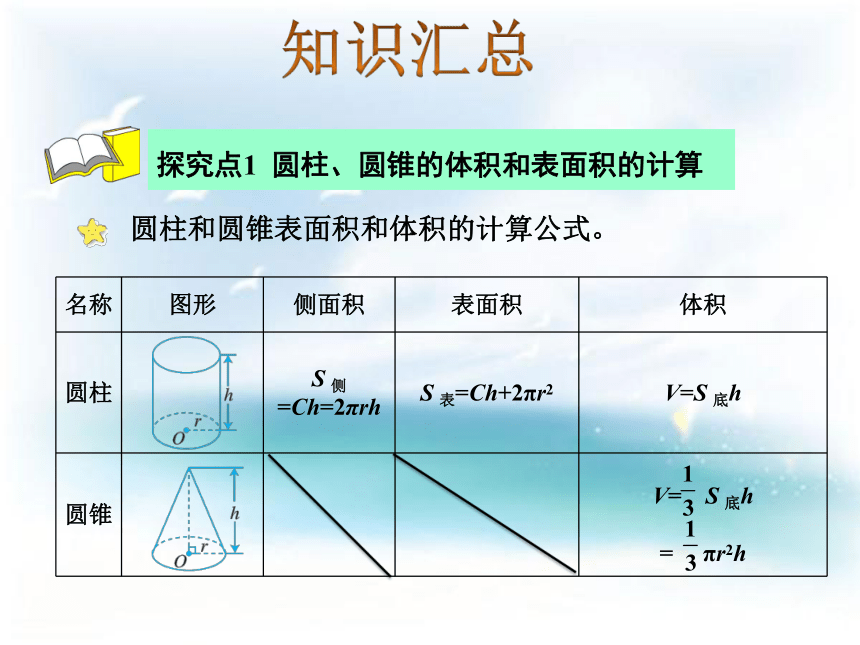
——圆柱和圆锥 7 整理和复习SJ 六年级下册 问题导入1.圆柱和圆锥表面积和体积的计算公式。
2.利用立体图形的表面积和体积的计算公式能解决那些实际问题呢?1.圆柱、圆锥的体积和表面积的计算
2.切割后,表面积和体积的增减变化
3.体积和表面积的综合运用探究点总览圆柱和圆锥表面积和体积的计算公式。知识汇总 1.填空。
(1)一个圆柱的底面半径是2 dm,侧面积是226.08 dm2,这个圆柱的高是( )dm。
(2)如图,把底面周长为18.84厘米,高为10厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积是( )平方厘米,体积是( )立方厘米。18304.92282.6知识汇总(3)把一个棱长6厘米的正方体木块削成一个最大的圆锥,圆锥的体积是( )立方厘米。
(4)一个圆柱和圆锥的底面积之比是4∶3,高的比是2∶5,它们的体积之比是( )。
(5)将一个圆柱的侧面展开后正好是一个边长为62.8厘米的正方形,这个圆柱的侧面积是( )平方厘米,体积是( )立方厘米。56.528∶53943.8419719.2知识汇总2.算一算,填一填。
(1)把一个底面直径为4厘米的圆柱切成两个半圆柱,表面积增加了48平方厘米。原来圆柱的表面积是( )平方厘米,体积是( )立方厘米。100.4875.36知识汇总(2)把一根长2米的圆柱形木料截成三段,表面积增加了约8平方分米,这根木料原来的体积约( )立方分米。
(3)一个圆锥的底面周长是18.84厘米,高是4厘米,从圆锥的顶点沿着高将它切成两半后,表面积之和比原来增加了( )平方厘米。4024知识汇总利用立体图形的表面积和体积的计算公式能解决那些实际问题呢?解答求立体图形的表面积的有关问题时,要注意弄清题中要求的到底是哪几部分,具体情况要具体对待。知识汇总3.判断。
(1)把圆锥的侧面展开,能得到一个等腰三角形。 ( )
(2)圆柱的底面半径和高都扩大为原来的2倍,则体积扩大为原来的4倍。 ( )
(3)圆柱的体积比与它等底等高的圆锥的体积多 。( )
(4)底面周长和高分别相等的正方体、长方体、圆柱和圆锥,圆柱的体积最大。 ( )×××√知识汇总4.选择。
(1)一张长28.26 cm,宽15 cm的长方形铁皮,要做成一个容积最大的圆柱形容器,应配上直径是( )cm的圆形铁皮。
A.2.5 B.4.5 C.5 D.9
(2)如图,酒瓶中装有一些酒,倒入一只酒杯中,酒杯的底面直径是酒瓶下底面直径的一半,共能倒满( )。A.10杯 B.15杯
C.20杯 D.24杯DD知识汇总(3)用丝带捆扎一种礼品盒(如右图),打结处长25厘米,要捆扎这种礼品盒,至少准备( )分米长的丝带。
A.18 B.21.5
C.22.5 D.30C知识汇总(4)两个正方体的体积之差为20 cm3,如果将这两个正方体分别加工成两个最大的圆柱(如下图),那么这两个圆柱的体积差( )。A.小于20 cm3
B.等于20 cm3
C.大于20 cm3
D.以上三种答案都有可能A知识汇总(5)一个圆柱和一个圆锥的体积相等,底面直径之比是3∶4,圆锥与圆柱的高的比是( )。
A.9∶16 B.16∶27
C.27∶16 D.16∶9C知识汇总知识汇总辨析:求旋转立体图形的体积时找不准对应的量5.直角三角形三边长分别为3 cm、4 cm和5 cm,以5 cm的边所在的直线为轴旋转一周,请画出旋转后形成的立体图形并求它的体积。画图略。3×4÷5=2.4(cm)
×5×2.42×3.14=30.144(cm3)
答:体积是30.144cm3。作 业 请完成教材P94~P96的练习与实践对应的习题。
补充作业 请完成“应用提升练”和“思维拓展练”习题
课后作业 1.求不规则图形的体积
2.抓住“水体积不变”解题
3.根据瓶正放和倒放的关系解决问题
6.一个零件的形状如下图所示,求出它的体积。3.14×( ) 2 ×(6+10)÷2=56.52(cm3)7.求下面图形的体积。(单位:cm)3.14×[( ) 2 -( ) 2]×10=219.8(cm3)3.14×( ) 2 ×(6+3÷3)=87.92(cm3) 8.有甲、乙两个圆柱形容器,从里面量它们的半径分别是10厘米和5厘米,两个容器内分别盛有10厘米高和15厘米高的水,现将乙容器中的一部分水倒入甲容器内,使得两个容器内的水面相平。这时两个容器内水的高度都为多少厘米?解:设这时两个容器内水的高度为x厘米。
3.14×10 2 ×x+3.14×5 2 ×x=3.14×10 2 ×10+3.14×5 2 ×15 x=11
答:这时两个容器内水的高度都为11厘米。9.长方体容器里盛有10厘米深的水,把一个底面半径是2厘米的圆柱垂直插入水中至底面(没有浸没)。当把这个圆柱向上提起并使它离开底面3厘米时,水面下降了4厘米。这个长方体容器的底面积是多少?(3.14×2×2× )+3.14×2×2=21.98(平方厘米)10.有一种饮料瓶的瓶身是圆柱形(不包括瓶颈),容积是300毫升,现在瓶中装有一些饮料,正放时饮料的高度为20厘米,倒放时空余部分的高度为5厘米(如下图)。则瓶内现有饮料多少毫升?300÷(20+5)×20=240(毫升)
答:现有饮料240毫升。11.两个相同的圆锥形容器中各装有一些水,水深都是圆锥高度的 。那么甲、乙两容器哪一个水多?多的是少的多少倍?12.如图是高约为7.75 cm的圆锥的侧面展开图,求这个圆锥的体积。3.14×2×8÷4=12.56(cm)
12.56÷3.14÷2=2(cm)
×3.14×2 2 ×7.75≈32.47(cm3) Thank you!
——圆柱和圆锥 7 整理和复习SJ 六年级下册 问题导入1.圆柱和圆锥表面积和体积的计算公式。
2.利用立体图形的表面积和体积的计算公式能解决那些实际问题呢?1.圆柱、圆锥的体积和表面积的计算
2.切割后,表面积和体积的增减变化
3.体积和表面积的综合运用探究点总览圆柱和圆锥表面积和体积的计算公式。知识汇总 1.填空。
(1)一个圆柱的底面半径是2 dm,侧面积是226.08 dm2,这个圆柱的高是( )dm。
(2)如图,把底面周长为18.84厘米,高为10厘米的圆柱切成若干等份,拼成一个近似的长方体。这个长方体的表面积是( )平方厘米,体积是( )立方厘米。18304.92282.6知识汇总(3)把一个棱长6厘米的正方体木块削成一个最大的圆锥,圆锥的体积是( )立方厘米。
(4)一个圆柱和圆锥的底面积之比是4∶3,高的比是2∶5,它们的体积之比是( )。
(5)将一个圆柱的侧面展开后正好是一个边长为62.8厘米的正方形,这个圆柱的侧面积是( )平方厘米,体积是( )立方厘米。56.528∶53943.8419719.2知识汇总2.算一算,填一填。
(1)把一个底面直径为4厘米的圆柱切成两个半圆柱,表面积增加了48平方厘米。原来圆柱的表面积是( )平方厘米,体积是( )立方厘米。100.4875.36知识汇总(2)把一根长2米的圆柱形木料截成三段,表面积增加了约8平方分米,这根木料原来的体积约( )立方分米。
(3)一个圆锥的底面周长是18.84厘米,高是4厘米,从圆锥的顶点沿着高将它切成两半后,表面积之和比原来增加了( )平方厘米。4024知识汇总利用立体图形的表面积和体积的计算公式能解决那些实际问题呢?解答求立体图形的表面积的有关问题时,要注意弄清题中要求的到底是哪几部分,具体情况要具体对待。知识汇总3.判断。
(1)把圆锥的侧面展开,能得到一个等腰三角形。 ( )
(2)圆柱的底面半径和高都扩大为原来的2倍,则体积扩大为原来的4倍。 ( )
(3)圆柱的体积比与它等底等高的圆锥的体积多 。( )
(4)底面周长和高分别相等的正方体、长方体、圆柱和圆锥,圆柱的体积最大。 ( )×××√知识汇总4.选择。
(1)一张长28.26 cm,宽15 cm的长方形铁皮,要做成一个容积最大的圆柱形容器,应配上直径是( )cm的圆形铁皮。
A.2.5 B.4.5 C.5 D.9
(2)如图,酒瓶中装有一些酒,倒入一只酒杯中,酒杯的底面直径是酒瓶下底面直径的一半,共能倒满( )。A.10杯 B.15杯
C.20杯 D.24杯DD知识汇总(3)用丝带捆扎一种礼品盒(如右图),打结处长25厘米,要捆扎这种礼品盒,至少准备( )分米长的丝带。
A.18 B.21.5
C.22.5 D.30C知识汇总(4)两个正方体的体积之差为20 cm3,如果将这两个正方体分别加工成两个最大的圆柱(如下图),那么这两个圆柱的体积差( )。A.小于20 cm3
B.等于20 cm3
C.大于20 cm3
D.以上三种答案都有可能A知识汇总(5)一个圆柱和一个圆锥的体积相等,底面直径之比是3∶4,圆锥与圆柱的高的比是( )。
A.9∶16 B.16∶27
C.27∶16 D.16∶9C知识汇总知识汇总辨析:求旋转立体图形的体积时找不准对应的量5.直角三角形三边长分别为3 cm、4 cm和5 cm,以5 cm的边所在的直线为轴旋转一周,请画出旋转后形成的立体图形并求它的体积。画图略。3×4÷5=2.4(cm)
×5×2.42×3.14=30.144(cm3)
答:体积是30.144cm3。作 业 请完成教材P94~P96的练习与实践对应的习题。
补充作业 请完成“应用提升练”和“思维拓展练”习题
课后作业 1.求不规则图形的体积
2.抓住“水体积不变”解题
3.根据瓶正放和倒放的关系解决问题
6.一个零件的形状如下图所示,求出它的体积。3.14×( ) 2 ×(6+10)÷2=56.52(cm3)7.求下面图形的体积。(单位:cm)3.14×[( ) 2 -( ) 2]×10=219.8(cm3)3.14×( ) 2 ×(6+3÷3)=87.92(cm3) 8.有甲、乙两个圆柱形容器,从里面量它们的半径分别是10厘米和5厘米,两个容器内分别盛有10厘米高和15厘米高的水,现将乙容器中的一部分水倒入甲容器内,使得两个容器内的水面相平。这时两个容器内水的高度都为多少厘米?解:设这时两个容器内水的高度为x厘米。
3.14×10 2 ×x+3.14×5 2 ×x=3.14×10 2 ×10+3.14×5 2 ×15 x=11
答:这时两个容器内水的高度都为11厘米。9.长方体容器里盛有10厘米深的水,把一个底面半径是2厘米的圆柱垂直插入水中至底面(没有浸没)。当把这个圆柱向上提起并使它离开底面3厘米时,水面下降了4厘米。这个长方体容器的底面积是多少?(3.14×2×2× )+3.14×2×2=21.98(平方厘米)10.有一种饮料瓶的瓶身是圆柱形(不包括瓶颈),容积是300毫升,现在瓶中装有一些饮料,正放时饮料的高度为20厘米,倒放时空余部分的高度为5厘米(如下图)。则瓶内现有饮料多少毫升?300÷(20+5)×20=240(毫升)
答:现有饮料240毫升。11.两个相同的圆锥形容器中各装有一些水,水深都是圆锥高度的 。那么甲、乙两容器哪一个水多?多的是少的多少倍?12.如图是高约为7.75 cm的圆锥的侧面展开图,求这个圆锥的体积。3.14×2×8÷4=12.56(cm)
12.56÷3.14÷2=2(cm)
×3.14×2 2 ×7.75≈32.47(cm3) Thank you!
