2018泰安中考数学总复习专题三:几何变换压轴题
文档属性
| 名称 | 2018泰安中考数学总复习专题三:几何变换压轴题 |

|
|
| 格式 | zip | ||
| 文件大小 | 377.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-17 18:40:41 | ||
图片预览



文档简介
聚焦泰安
类型一 图形的旋转变换
几何图形的旋转变换是近年来中考中的常考点,多与三角形、四边形相结合.解决旋转变换问题,首先要明确旋转中心、旋转方向和旋转角,关键是找出旋转前后的对应点,利用旋转前后两图形全等等性质解题.
(2016·潍坊)如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
(1)如图1,连接AC分别交DE,DF于点M,N,
求证:MN=AC;
(2)如图2,将∠EDF以点D为旋转中心旋转,其两边DE′,DF′分别与直线AB,BC相交于点G,P.连接GP,当△DGP的面积等于3时,求旋转角的大小并指明旋转方向.
【分析】 (1)连接BD,由∠BAD=60°,得到△ABD为等边三角形,进而证明点E是AB的中点,再根据相似三角形的性质解答;(2)分∠EDF顺时针旋转和逆时针旋转两种情况,然后根据旋转的性质解题.
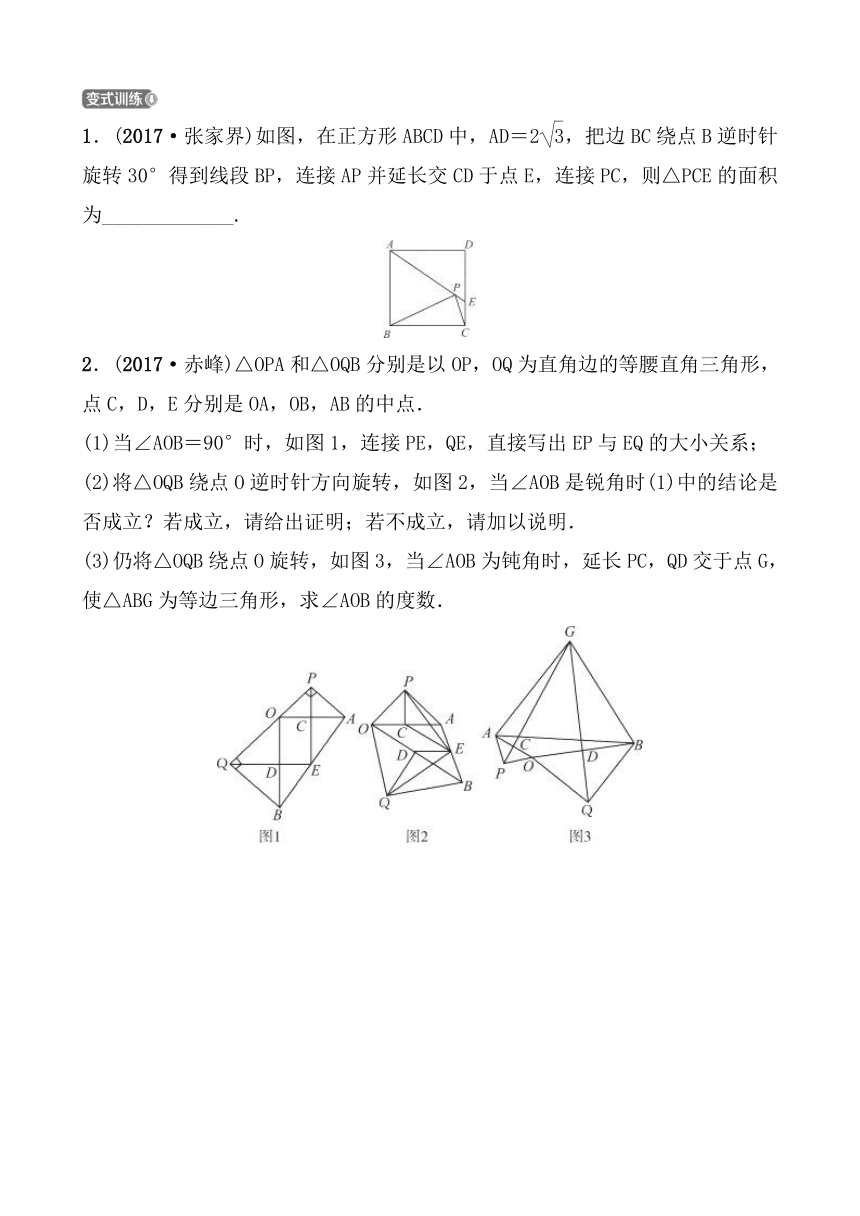
1.(2017·张家界)如图,在正方形ABCD中,AD=2,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则△PCE的面积为_____________.
2.(2017·赤峰)△OPA和△OQB分别是以OP,OQ为直角边的等腰直角三角形,点C,D,E分别是OA,OB,AB的中点.
(1)当∠AOB=90°时,如图1,连接PE,QE,直接写出EP与EQ的大小关系;
(2)将△OQB绕点O逆时针方向旋转,如图2,当∠AOB是锐角时(1)中的结论是否成立?若成立,请给出证明;若不成立,请加以说明.
(3)仍将△OQB绕点O旋转,如图3,当∠AOB为钝角时,延长PC,QD交于点G,使△ABG为等边三角形,求∠AOB的度数.
类型二 图形的翻折变换
几何图形的翻折变换也是近年来中考中的常考点,多与三角形、四边形相结合.翻折变换的实质是对称,翻折部分的两图形全等,找出对应边、对应角,再结合勾股定理、相似的性质与判定解题.
(2017·南宁)如图,菱形ABCD的对角线相交于点O,AC=2,BD=2,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为 .
【分析】 根据菱形的性质和折叠的性质推出△BEF是等边三角形,得到∠BEF=60°,得到△AEO是等边三角形,推出EF是△ABC的中位线,从而得到结论.
3.(2016·张家界)如图,将矩形ABCD沿GH对折,点C落在点Q处,点D落在点E处,EQ与BC交于点F.若AD=8 cm,AB=6 cm,AE=4 cm,则△EBF的周长是________cm.
4.(2017·锦州)如图,正方形ABCD中,AB=2,E是CD中点,将正方形ABCD沿AM折叠,使点B的对应点F落在AE上,延长MF交CD于点N,则DN的长为 __________.
类型三 图形的相似
图形的相似常以三角形、四边形为背景,与旋转、翻折、动点相结合,考查三角形相似的性质及判定,难度较大,是中考中常考的几何压轴题.与动点相关的相似三角形,要根据动点的运动情况讨论相似三角形的对应边、对应角,进而判定相似三角形,再利用相似三角形的性质解题.
(2016·青岛)如图,在矩形ABCD中,AB=6 cm,BC=8 cm,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动,速度为1 cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1 cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6) ,解答下列问题:
(1)当t为何值时,△AOP是等腰三角形;
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式.
【分析】 (1)根据勾股定理求出AC的值,然后分类讨论:当AP=PO时,求出t的值;当AP=AO时,求出t的值;(2)过点E作EH⊥AC于点H,过点Q作QM⊥AC于点M,过点D作DN⊥AC于点N,交QF于点G,分别用t表示出EH,DN,DG,再利用面积的和差计算即可.
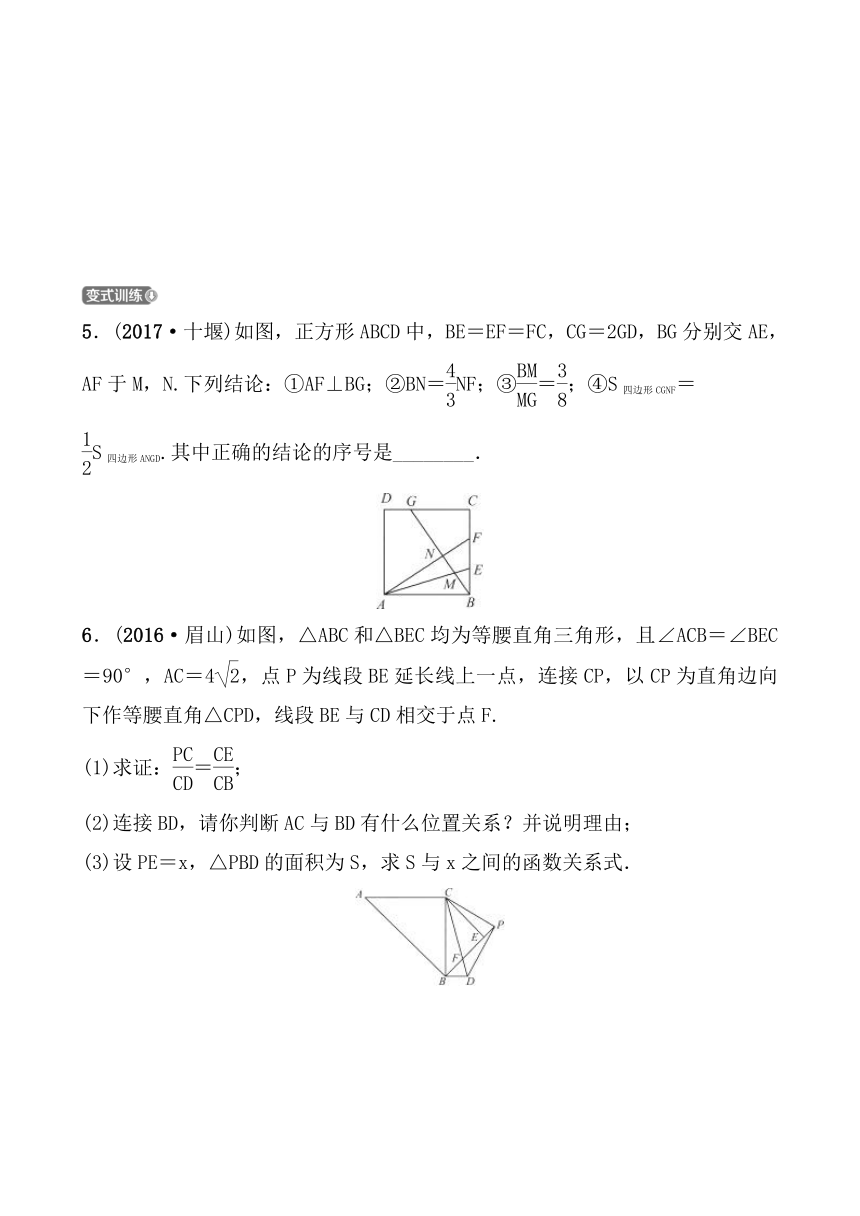
5.(2017·十堰)如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=NF;③=;④S四边形CGNF=
S四边形ANGD.其中正确的结论的序号是________.
6.(2016·眉山)如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4,点P为线段BE延长线上一点,连接CP,以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F.
(1)求证:=;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式.
参考答案
【聚焦泰安】
【例1】 (1)如图,连接BD,设BD交AC于点O,
∵在菱形ABCD中,∠DAB=60°,AD=AB,
∴△ABD为等边三角形.
∵DE⊥AB,∴点E为AB的中点.
∵AE∥CD,∴==.同理=.
∴M,N是线段AC的三等分点,∴MN=AC.
(2)∵AB∥CD,∠BAD=60°,∴∠ADC=120°.
∵∠ADE=∠CDF=30°,∴∠EDF=60°.
当∠EDF顺时针旋转时,由旋转的性质知,
∠EDG=∠FDP,∠GDP=∠EDF=60°.
∵DE=DF=,∠DEG=∠DFP=90°,
∴△DEG≌△DFP,∴DG=DP,
∴△DGP是等边三角形.则S△DGP=DG2.
由DG2=3,又∵DG>0,解得DG=2.
∴cos∠EDG===,∴∠EDG=60°.
∴当顺时针旋转60°时,△DGP的面积是3.
同理,当逆时针旋转60°时,△DGP的面积也是3.
综上所述,当∠EDF以点D为旋转中心,顺时针或逆时针旋转60°时,△DGP的面积是3.
变式训练 1.9-5
2.解:(1)EP=EQ.
(2)结论成立.证明如下:
∵点C,E分别是OA,AB的中点,
∴CE∥OB,CE=OB,∴∠DOC=∠ECA.
∵点D是Rt△OQB斜边中点,
∴DQ=OB,∴CE=DQ.
同理,PC=DE,∠DOC=∠BDE,∴∠ECA=∠BDE,
∴∠PCE=∠EDQ,∴△EPC≌△QED,∴EP=EQ.
(3)如图,连接GO,
∵点D,C分别是OB,OA的中点,△APO与△QBO都是等腰直角三角形,
∴CQ,GP分别是OB,OA的垂直平分线,
∴GB=GO=GA,
∴∠GBO=∠GOB,∠GOA=∠GAO.
设∠GOB=x,∠GOA=y,
则x+x+y+y+60°=360°,
∴x+y=150°,∴∠AOB=150°.
【例2】 ∵四边形ABCD是菱形,AC=2,BD=2,
∴∠ABO=∠CBO,AC⊥BD.
∵AO=1,BO=,∴tan∠ABO==,
∴∠ABO=30°,AB=2,∴∠ABC=60°.
由折叠的性质得EF⊥BO,OE=BE,∠BEF=∠OEF,
∴BE=BF,EF∥AC,∴△BEF是等边三角形,
∴∠BEF=60°,∴∠OEF=60°,∴∠AEO=60°,
∴△AEO是等边三角形,∴AE=OE,∴BE=AE,
∴EF是△ABC的中位线,
∴EF=AC=1,AE=OE=1,
同理CF=OF=1,
∴五边形AEFCD的周长=1+1+1+2+2=7.
故答案为7.
变式训练 3.8 4.2-4
【例3】 (1)∵在矩形ABCD中,AB=6 cm,BC=8 cm,
∴AC=10 cm.
①当AP=PO时,如图,过点P作PM⊥AO,
∴AM=AO=.
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ACD,∴=,∴AP=t=.
②当AP=AO时,t=5.
∵0<t<6,∴t=或t=5均符合题意,
∴当t=或t=5时,△AOP是等腰三角形.
(2)如图,过点E作EH⊥AC于点H,过点Q作QM⊥AC于点M,过点D作DN⊥AC于点N,交QF于点G,
∵四边形ABCD是矩形,∴AD∥BC,
∴∠PAO=∠ECO.
∵点O是对角线AC的中点,∴AO=CO.
又∵∠AOP=∠COE,∴△AOP≌△COE,
∴CE=AP=t.
∵△CEH∽△CAB,
∴=,∴EH=.
∵S△ADC=AD·DC=DN·AC,
∴DN==.
∵QM∥DN,∴△CQM∽△CDN,
∴=,即=.∴QM=,
∴DG=-=.
∵FQ∥AC,∴△DFQ∽△DOC,
∴=,∴FQ=,
∴S=S△OEC+S△OCD-S△DFQ
=OC·EH+OC·DN-DG·FQ
=-t2+t+12.
即S与t的函数关系式为S=-t2+t+12.
变式训练 5.①③
6.解:(1)∵△ABC和△BEC均为等腰直角三角形,
∴∠ECB=∠PCD=45°,∠CEB=∠CPD=90°,
∴△BCE∽△DCP,∴=.
(2)AC∥BD.理由如下:
∵∠PCE+∠ECD=∠BCD+∠ECD=45°,
∴∠PCE=∠DCB.
∵=,∴△PCE∽△DCB,
∴∠CBD=∠CEP=90°.
∵∠ACB=90°,∴∠ACB=∠CBD,∴AC∥BD.
(3)如图,过点P作PM⊥BD的延长线于点M,
∵AC=4,△ABC和△BEC均为等腰直角三角形,
∴BE=CE=4.
∵△PCE∽△DCB,∴=,即=,
∴BD=x.
∵∠PBM=∠CBD-∠CBP=45°,
BP=BE+PE=4+x,∴PM=,
∴S=BD·PM=×x×=x2+2x.
类型一 图形的旋转变换
几何图形的旋转变换是近年来中考中的常考点,多与三角形、四边形相结合.解决旋转变换问题,首先要明确旋转中心、旋转方向和旋转角,关键是找出旋转前后的对应点,利用旋转前后两图形全等等性质解题.
(2016·潍坊)如图,在菱形ABCD中,AB=2,∠BAD=60°,过点D作DE⊥AB于点E,DF⊥BC于点F.
(1)如图1,连接AC分别交DE,DF于点M,N,
求证:MN=AC;
(2)如图2,将∠EDF以点D为旋转中心旋转,其两边DE′,DF′分别与直线AB,BC相交于点G,P.连接GP,当△DGP的面积等于3时,求旋转角的大小并指明旋转方向.
【分析】 (1)连接BD,由∠BAD=60°,得到△ABD为等边三角形,进而证明点E是AB的中点,再根据相似三角形的性质解答;(2)分∠EDF顺时针旋转和逆时针旋转两种情况,然后根据旋转的性质解题.
1.(2017·张家界)如图,在正方形ABCD中,AD=2,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则△PCE的面积为_____________.
2.(2017·赤峰)△OPA和△OQB分别是以OP,OQ为直角边的等腰直角三角形,点C,D,E分别是OA,OB,AB的中点.
(1)当∠AOB=90°时,如图1,连接PE,QE,直接写出EP与EQ的大小关系;
(2)将△OQB绕点O逆时针方向旋转,如图2,当∠AOB是锐角时(1)中的结论是否成立?若成立,请给出证明;若不成立,请加以说明.
(3)仍将△OQB绕点O旋转,如图3,当∠AOB为钝角时,延长PC,QD交于点G,使△ABG为等边三角形,求∠AOB的度数.
类型二 图形的翻折变换
几何图形的翻折变换也是近年来中考中的常考点,多与三角形、四边形相结合.翻折变换的实质是对称,翻折部分的两图形全等,找出对应边、对应角,再结合勾股定理、相似的性质与判定解题.
(2017·南宁)如图,菱形ABCD的对角线相交于点O,AC=2,BD=2,将菱形按如图方式折叠,使点B与点O重合,折痕为EF,则五边形AEFCD的周长为 .
【分析】 根据菱形的性质和折叠的性质推出△BEF是等边三角形,得到∠BEF=60°,得到△AEO是等边三角形,推出EF是△ABC的中位线,从而得到结论.
3.(2016·张家界)如图,将矩形ABCD沿GH对折,点C落在点Q处,点D落在点E处,EQ与BC交于点F.若AD=8 cm,AB=6 cm,AE=4 cm,则△EBF的周长是________cm.
4.(2017·锦州)如图,正方形ABCD中,AB=2,E是CD中点,将正方形ABCD沿AM折叠,使点B的对应点F落在AE上,延长MF交CD于点N,则DN的长为 __________.
类型三 图形的相似
图形的相似常以三角形、四边形为背景,与旋转、翻折、动点相结合,考查三角形相似的性质及判定,难度较大,是中考中常考的几何压轴题.与动点相关的相似三角形,要根据动点的运动情况讨论相似三角形的对应边、对应角,进而判定相似三角形,再利用相似三角形的性质解题.
(2016·青岛)如图,在矩形ABCD中,AB=6 cm,BC=8 cm,对角线AC,BD交于点O.点P从点A出发,沿AD方向匀速运动,速度为1 cm/s;同时,点Q从点D出发,沿DC方向匀速运动,速度为1 cm/s;当一个点停止运动时,另一个点也停止运动.连接PO并延长,交BC于点E,过点Q作QF∥AC,交BD于点F.设运动时间为t(s)(0<t<6) ,解答下列问题:
(1)当t为何值时,△AOP是等腰三角形;
(2)设五边形OECQF的面积为S(cm2),试确定S与t的函数关系式.
【分析】 (1)根据勾股定理求出AC的值,然后分类讨论:当AP=PO时,求出t的值;当AP=AO时,求出t的值;(2)过点E作EH⊥AC于点H,过点Q作QM⊥AC于点M,过点D作DN⊥AC于点N,交QF于点G,分别用t表示出EH,DN,DG,再利用面积的和差计算即可.
5.(2017·十堰)如图,正方形ABCD中,BE=EF=FC,CG=2GD,BG分别交AE,AF于M,N.下列结论:①AF⊥BG;②BN=NF;③=;④S四边形CGNF=
S四边形ANGD.其中正确的结论的序号是________.
6.(2016·眉山)如图,△ABC和△BEC均为等腰直角三角形,且∠ACB=∠BEC=90°,AC=4,点P为线段BE延长线上一点,连接CP,以CP为直角边向下作等腰直角△CPD,线段BE与CD相交于点F.
(1)求证:=;
(2)连接BD,请你判断AC与BD有什么位置关系?并说明理由;
(3)设PE=x,△PBD的面积为S,求S与x之间的函数关系式.
参考答案
【聚焦泰安】
【例1】 (1)如图,连接BD,设BD交AC于点O,
∵在菱形ABCD中,∠DAB=60°,AD=AB,
∴△ABD为等边三角形.
∵DE⊥AB,∴点E为AB的中点.
∵AE∥CD,∴==.同理=.
∴M,N是线段AC的三等分点,∴MN=AC.
(2)∵AB∥CD,∠BAD=60°,∴∠ADC=120°.
∵∠ADE=∠CDF=30°,∴∠EDF=60°.
当∠EDF顺时针旋转时,由旋转的性质知,
∠EDG=∠FDP,∠GDP=∠EDF=60°.
∵DE=DF=,∠DEG=∠DFP=90°,
∴△DEG≌△DFP,∴DG=DP,
∴△DGP是等边三角形.则S△DGP=DG2.
由DG2=3,又∵DG>0,解得DG=2.
∴cos∠EDG===,∴∠EDG=60°.
∴当顺时针旋转60°时,△DGP的面积是3.
同理,当逆时针旋转60°时,△DGP的面积也是3.
综上所述,当∠EDF以点D为旋转中心,顺时针或逆时针旋转60°时,△DGP的面积是3.
变式训练 1.9-5
2.解:(1)EP=EQ.
(2)结论成立.证明如下:
∵点C,E分别是OA,AB的中点,
∴CE∥OB,CE=OB,∴∠DOC=∠ECA.
∵点D是Rt△OQB斜边中点,
∴DQ=OB,∴CE=DQ.
同理,PC=DE,∠DOC=∠BDE,∴∠ECA=∠BDE,
∴∠PCE=∠EDQ,∴△EPC≌△QED,∴EP=EQ.
(3)如图,连接GO,
∵点D,C分别是OB,OA的中点,△APO与△QBO都是等腰直角三角形,
∴CQ,GP分别是OB,OA的垂直平分线,
∴GB=GO=GA,
∴∠GBO=∠GOB,∠GOA=∠GAO.
设∠GOB=x,∠GOA=y,
则x+x+y+y+60°=360°,
∴x+y=150°,∴∠AOB=150°.
【例2】 ∵四边形ABCD是菱形,AC=2,BD=2,
∴∠ABO=∠CBO,AC⊥BD.
∵AO=1,BO=,∴tan∠ABO==,
∴∠ABO=30°,AB=2,∴∠ABC=60°.
由折叠的性质得EF⊥BO,OE=BE,∠BEF=∠OEF,
∴BE=BF,EF∥AC,∴△BEF是等边三角形,
∴∠BEF=60°,∴∠OEF=60°,∴∠AEO=60°,
∴△AEO是等边三角形,∴AE=OE,∴BE=AE,
∴EF是△ABC的中位线,
∴EF=AC=1,AE=OE=1,
同理CF=OF=1,
∴五边形AEFCD的周长=1+1+1+2+2=7.
故答案为7.
变式训练 3.8 4.2-4
【例3】 (1)∵在矩形ABCD中,AB=6 cm,BC=8 cm,
∴AC=10 cm.
①当AP=PO时,如图,过点P作PM⊥AO,
∴AM=AO=.
∵∠PMA=∠ADC=90°,∠PAM=∠CAD,
∴△APM∽△ACD,∴=,∴AP=t=.
②当AP=AO时,t=5.
∵0<t<6,∴t=或t=5均符合题意,
∴当t=或t=5时,△AOP是等腰三角形.
(2)如图,过点E作EH⊥AC于点H,过点Q作QM⊥AC于点M,过点D作DN⊥AC于点N,交QF于点G,
∵四边形ABCD是矩形,∴AD∥BC,
∴∠PAO=∠ECO.
∵点O是对角线AC的中点,∴AO=CO.
又∵∠AOP=∠COE,∴△AOP≌△COE,
∴CE=AP=t.
∵△CEH∽△CAB,
∴=,∴EH=.
∵S△ADC=AD·DC=DN·AC,
∴DN==.
∵QM∥DN,∴△CQM∽△CDN,
∴=,即=.∴QM=,
∴DG=-=.
∵FQ∥AC,∴△DFQ∽△DOC,
∴=,∴FQ=,
∴S=S△OEC+S△OCD-S△DFQ
=OC·EH+OC·DN-DG·FQ
=-t2+t+12.
即S与t的函数关系式为S=-t2+t+12.
变式训练 5.①③
6.解:(1)∵△ABC和△BEC均为等腰直角三角形,
∴∠ECB=∠PCD=45°,∠CEB=∠CPD=90°,
∴△BCE∽△DCP,∴=.
(2)AC∥BD.理由如下:
∵∠PCE+∠ECD=∠BCD+∠ECD=45°,
∴∠PCE=∠DCB.
∵=,∴△PCE∽△DCB,
∴∠CBD=∠CEP=90°.
∵∠ACB=90°,∴∠ACB=∠CBD,∴AC∥BD.
(3)如图,过点P作PM⊥BD的延长线于点M,
∵AC=4,△ABC和△BEC均为等腰直角三角形,
∴BE=CE=4.
∵△PCE∽△DCB,∴=,即=,
∴BD=x.
∵∠PBM=∠CBD-∠CBP=45°,
BP=BE+PE=4+x,∴PM=,
∴S=BD·PM=×x×=x2+2x.
同课章节目录
