2018年泰安中考数学总复习专题四:函数压轴题
文档属性
| 名称 | 2018年泰安中考数学总复习专题四:函数压轴题 |
|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-17 18:49:37 | ||
图片预览




文档简介
聚焦泰安
类型一 动点函数图象问题
此类问题一般是通过分析动点在几何图形边上的运动情况,确定出有关动点函数图象的变化情况.分析此类问题,首先要明确动点在哪条边上运动,在运动过程中引起了哪个量的变化,然后求出在运动过程中对应的函数关系式,最后根据函数关系式判别图象的变化.
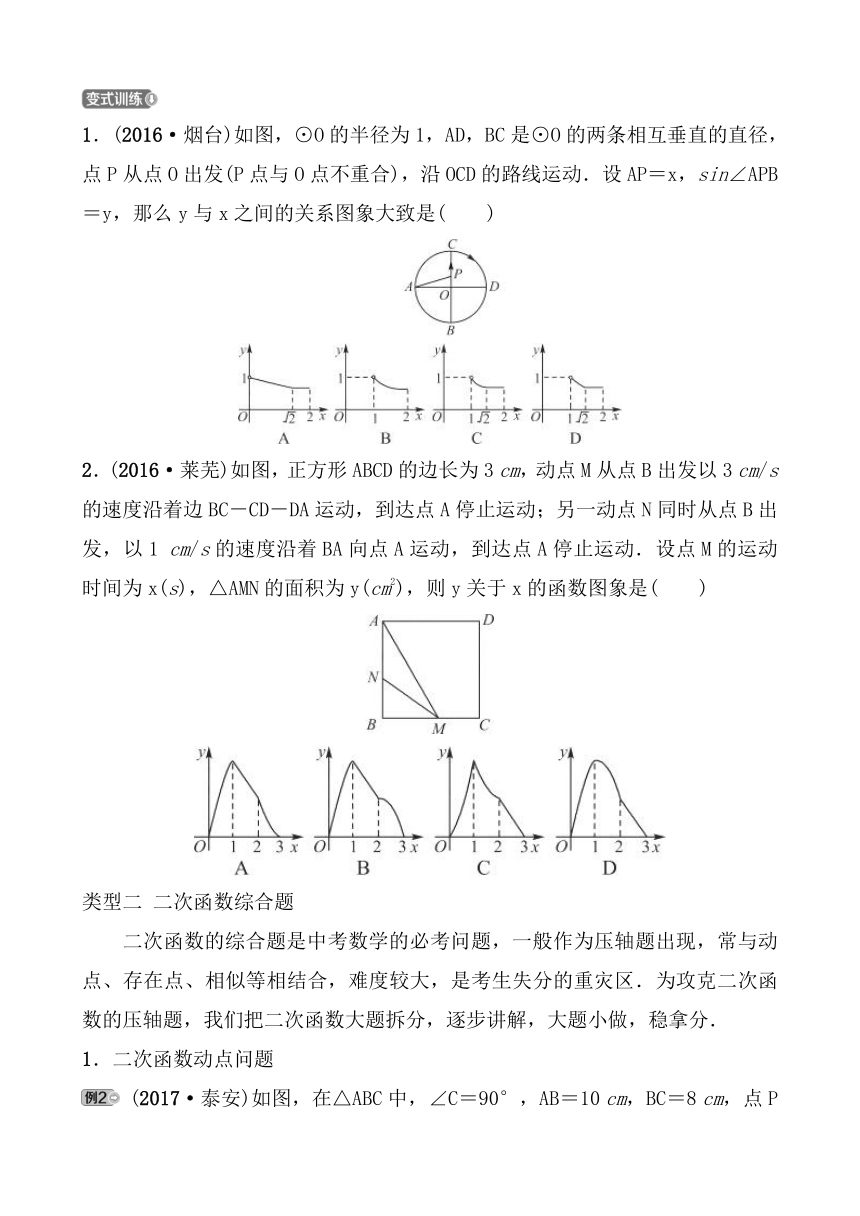
(2016·济南)如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M,N,E分别是AB,AD,CB上的点,AM=CE=1,AN=3.点P从点M出发,以每秒1个单位长度的速度沿折线MB-BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND-DC-CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t s,则S与t之间的函数关系的大致图象为( )
【分析】 由点Q从点N出发,沿折线ND-DC-CE向点E运动,确定出点Q分别在ND,DC,CE运动时对应的t的取值范围,再根据t所在的取值范围分别求出其对应的函数关系式,最后根据函数关系式确定对应的函数图象.
1.(2016·烟台)如图,⊙O的半径为1,AD,BC是⊙O的两条相互垂直的直径,点P从点O出发(P点与O点不重合),沿OCD的路线运动.设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )
2.(2016·莱芜)如图,正方形ABCD的边长为3 cm,动点M从点B出发以3 cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动;另一动点N同时从点B出发,以1 cm/s的速度沿着BA向点A运动,到达点A停止运动.设点M的运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
类型二 二次函数综合题
二次函数的综合题是中考数学的必考问题,一般作为压轴题出现,常与动点、存在点、相似等相结合,难度较大,是考生失分的重灾区.为攻克二次函数的压轴题,我们把二次函数大题拆分,逐步讲解,大题小做,稳拿分.
1.二次函数动点问题
(2017·泰安)如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点P从点A沿AC向点C以1 cm/s的速度运动,同时点Q从点C沿CB向点B以2 cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19 cm2 B.16 cm2
C.15 cm2 D.12 cm2
【分析】 首先利用勾股定理可得出AC的长,再设运动时间为t(0≤t≤4),利用分割图形求面积法可得出S四边形PABQ,利用配方法即可求出四边形PABQ的面积最小值.
3.(2017·新疆)如图,在边长为6 cm的正方形ABCD中,点E,F,G,H分别从点A,B,C,D同时出发,均以1 cm/s的速度向点B,C,D,A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为___ s时,四边形EFGH的面积最小,其最小值是______cm2.
4.(2016·德州)已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的表达式;
(2)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
2.二次函数存在点问题
(2017·苏州)如图,二次函数y=x2+bx+c的图象与x轴交于Α,Β两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b,c的值;
(2)如图1,连接BE,线段OC上的点F关于直线l的对称点F′恰好在线段BE上,求点F的坐标;
(3)如图2,动点Ρ在线段OB上,过点Ρ作x轴的垂线,分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段ΝQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
【分析】 (1)由条件可求得抛物线对称轴,则可求得b的值;由OB=OC,可用c表示出B点坐标,代入抛物线表达式可求得c的值;(2)可设F(0,m),则可表示出F′的坐标,由B,E的坐标可求得直线BE的表达式,把F′坐标代入直线BE表达式可得到关于m的方程,可求得F点的坐标;(3)设点P坐标为(n,0),可表示出PA,PB,PN的长,作QR⊥PN,垂足为R,则可求得QR的长,用n可表示出Q,R,N的坐标,在Rt△QRN中,由勾股定理可得到关于n的二次函数,利用二次函数的性质可知其取得最小值时n的值,则可求得Q点的坐标,
解决二次函数存在点问题,一般先假设该点存在,根据该点所在的直线或抛物线的表达式,设出该点的坐标;然后用该点的坐标表示出与该点有关的线段长或其他点的坐标等;最后结合题干中其他条件列出等式,求出该点的坐标,然后判别该点坐标是否符合题意,若符合题意,则该点存在,否则该点不存在.
5.(2016·日照)如图1,抛物线y=-[(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.
(1)求m,n的值;
(2)如图2,点M,P分别为线段BC和线段OB上的动点,连接PM,PC,是否存在这样的点P,使△PCM为等腰三角形、△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
3.二次函数相似问题
(2017·日照)如图,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
(1)求线段CD的长及顶点P的坐标;
(2)求抛物线的函数表达式;
(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.
【分析】 (1)由勾股定理可求得MN的长,在Rt△OCD中,可求得CD的长,则可求得P点坐标;(2)可设抛物线的表达式为顶点式,再把N点坐标代入可求得抛物线表达式;(3)由抛物线表达式可求得A,B的坐标,由S四边形OPMN=8S△QAB可求得点Q到x轴的距离,且点Q只能在x轴的下方,则可求得Q点的坐标,再证明△QAB∽△OBN即可.
二次函数相似问题常与动点、存在点相结合,利用动点或存在点的坐标表示出与相似三角形有关的线段长,要注意边的对应有多种可能,对每一种情况都要具体分析讨论,然后利用相似三角形的对应边成比例列出方程,通过解方程求得结果,还要考虑求出的结果是否符合题意及实际情况.
6.如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点,且AB⊥BC.
(1)求抛物线的表达式及点C的坐标;
(2)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
参考答案
【聚焦泰安】
【例1】 如图,过点D作DF⊥AB于点F,过点Q作QG⊥AB于点G,
当0≤t≤2时,点Q在线段ND上.
∵AB∥CD,∠B=90°,∴四边形BCDF是矩形,
∴DF=BC=4,
∴AF==3,
∴DC=BF=2,
∴AQ=AN+NQ=3+t,AP=AM+MP=1+t.
∵QG∥DF,∴△AQG∽△ADF,
∴=,即=,∴QG=(3+t),
∴S=AP·QG=×(1+t)×(3+t)=t2+t+,且当t=2时,点Q恰好运动到点D,S=6;
当2<t≤4时,点Q在线段DC上,
∴S=AP·BC=×(1+t)×4=2t+2;
当4<t≤5时,点P,Q均在BC上运动,BP=CQ=t-4,
∴PQ=BC-BP-CQ=12-2t,
∴S=AB·PQ=×5×(12-2t)=-5t+30,且当t=5时,点Q运动到点E后停止运动,此时S=5.
综上所述,S=
由函数关系式,S与t之间的函数关系的大致图象为C或D.
∵t=2时,S=6;t=5时,S=5,6>5,
∴S与t之间的函数关系的大致图象为D.故选D.
变式训练 1.C 2.A
【例2】 在Rt△ABC中,∠C=90°,
AB=10 cm,BC=8 cm,
∴AC==6 cm.
设运动时间为t(0≤t≤4),
则PC=(6-t)cm,CQ=2t cm,
∴S四边形PABQ=S△ABC-S△CPQ=AC·BC-PC·CQ=×6×8-(6-t)×2t=t2-6t+24=(t-3)2+15,
∴当t=3时,四边形PABQ的面积取最小值,最小值为15.故选C.
变式训练3.3 18
4.解:(1)解方程x2+4x+3=0得x1=-1,x2=-3.
∵m,n是方程x2+4x+3=0的两根,且|m|<|n|,
∴m=-1,n=-3.
把点A(-1,0),B(0,-3)代入y=x2+bx+c,
得
解得
∴这个抛物线的表达式为y=x2-2x-3.
(2)由B(0,-3),C(3,0),得直线BC的表达式为y=x-3.
∴设点P的坐标为(t,t-3).
∵PM⊥x轴,点M在抛物线上,
∴点M的坐标为(t,t2-2t-3).
如图,过点Q作QF⊥PM于点F,则△PQF为等腰直角三角形.
∵PQ=,∴QF=1.
如图,当点P在点M上方时,即0<t<3.
PM=(t-3)-(t2-2t-3)=-t2+3t,
∴S=PM·QF=(-t2+3t)=-t2+t.
如图,当点P在点M下方时,即t<0或t>3.
PM=(t2-2t-3)-(t-3)=t2-3t,
∴S=PM·QF=(t2-3t)=t2-t.
综上所述,S=
【例3】 (1)∵CD∥x轴,CD=2,
∴抛物线对称轴为直线l:x=1.
∴-=1,∴b=-2.
∵OB=OC,C(0,c),∴B点的坐标为(-c,0),
∵点B在抛物线上,
∴0=c2+2c+c,解得c=-3或c=0(舍去),∴c=-3.
(2)设点F的坐标为(0,m).
∵对称轴为直线l:x=1,
∴点F关于直线l的对称点F的坐标为(2,m).
∵直线BE经过点B(3,0),E(1,-4),
∴利用待定系数法可得直线BE的表达式为y=2x-6.
∵点F在BE上,
∴m=2×2-6=-2,即点F的坐标为(0,-2).
(3)存在点Q满足题意.
设点P坐标为(n,0),
则PA=n+1,PB=PM=3-n,PN=-n2+2n+3.
如图,作QR⊥PN,垂足为R,
∵S△PQN=S△APM,
∴(n+1)(3-n)=(-n2+2n+3)·QR,∴QR=1.
①点Q在直线PN的左侧时,Q点的坐标为(n-1,n2-4n),R点的坐标为(n,n2-4n),N点的坐标为(n,n2-2n-3).在Rt△QRN中,NQ2=1+(2n-3)2,
∴n=时,NQ取最小值1.此时Q点的坐标为(,-).
②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2-4).同理,NQ2=1+(2n-1)2,
∴n=时,NQ取最小值1.此时Q点的坐标为(,-).
综上所述,满足题意的点Q的坐标为(,-)和(,-).
变式训练
5.解:(1)∵抛物线的对称轴是x=2,
∴m-2+2m+3=4,解得m=1,
∴A(-1,0), B(5,0).
把A(-1,0)代入抛物线表达式,
得-(9+n)=0,解得n=-9,
∴m=1,n=-9.
(2)假设点P存在,设点P(x0,0)(0①当点P为△PMB的直角顶点时,CM=MP.
∵MP∥OC,∴=,=,
∴MP=(5-x0),CM=x0.
则(5-x0)=x0,解得x0=,
∴P(,0).
②当点M为△PMB的直角顶点时,则 CM=MP.
∵△PMB∽△COB,∴==,
∴PM=(5-x0),BM=(5-x0),
∴CM=-(5-x0)=.
则(5-x0)=,解得x0=,∴P(,0).
综上所述,满足条件的点P的坐标为(,0)或(,0).
【例4】 (1)∵O,M,N三点都在⊙C上,
且∠MON=90°,
∴MN为⊙C的直径,点C为MN的中点.
∵M(4,0),N(0,3),∴C(2,1.5),
MN==5,
∴CP=2.5,∴CD=1.5,顶点P的坐标为(2,-1).
(2)∵抛物线的顶点坐标为P(2,-1),
∴可设抛物线的表达式为y=a(x-2)2-1.
又∵抛物线过点N(0,3),∴3=4a-1,解得a=1,
故抛物线的表达式为y=(x-2)2-1=x2-4x+3.
(3)由题意得:
S四边形OPMN=S△OMN+S△OPM=×4×3+×4×1=8.
∵S四边形OPMN=8S△QAB,∴S△QAB=1.
当y=0时,x2-4x+3=0,
解得x=1或x=3,
∴A(1,0),B(3,0).
设Q(x,y),则S△QAB=|AB|·|y|=|y|=1.
∵△OBN为等腰直角三角形,且△QAB∽△OBN,
∴△QAB也应为等腰直角三角形.
当y=1时,结合图形易知,△QAB一定不是直角三角形,不合题意;
当y=-1时,点Q的坐标为(2,-1),
此时QA=QB=,AB=2,
∴△QAB为等腰直角三角形,符合题意.
综上可知,存在点Q(2,-1),使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立.
变式训练
6.解:(1)∵顶点A的坐标为(1,1),
∴设抛物线的表达式为y=a(x-1)2+1.
∵抛物线过原点,∴0=a(0-1)2+1,解得a=-1.
∴抛物线的表达式为y=-(x-1)2+1,
即y=-x2+2x.
令y=-x2+2x=x-2,解得x=2或x=-1.
当x=2时,y=2-2=0,即B(2,0).
当x=-1时,y=-1-2=-3,即C(-1,-3).
(2)假设存在满足条件的点N,
设N(x,0),则M (x,-x2+2x),
∴ON=|x|,MN=|-x2+2x|.
由A(1,1),B(2,0),C(-1,-3),
得AB=,BC=3.
∵AB⊥BC,MN⊥x轴于点N,
∴∠ABC=∠MNO=90°,
∴当△MNO∽△ABC时,有=,
即= ,
整理得|x|·|-x+2|=|x|.
当x=0时,M,O,N不能构成三角形,故x≠0.
∴|-x+2|=,解得x=或x=.
此时点N的坐标为(,0)或(,0).
当△ONM∽△ABC时,有=,
即=,
整理得|x|·|-x+2|=3|x|.
∵x≠0,∴|-x+2|=3,解得x=5或x=-1.
此时点N的坐标为(-1,0)或(5,0).
综上所述,存在满足条件的N点,其坐标为(,0)或(,0)或(-1,0)或(5,0).
类型一 动点函数图象问题
此类问题一般是通过分析动点在几何图形边上的运动情况,确定出有关动点函数图象的变化情况.分析此类问题,首先要明确动点在哪条边上运动,在运动过程中引起了哪个量的变化,然后求出在运动过程中对应的函数关系式,最后根据函数关系式判别图象的变化.
(2016·济南)如图,在四边形ABCD中,AB∥CD,∠B=90°,AB=AD=5,BC=4,M,N,E分别是AB,AD,CB上的点,AM=CE=1,AN=3.点P从点M出发,以每秒1个单位长度的速度沿折线MB-BE向点E运动,同时点Q从点N出发,以相同的速度沿折线ND-DC-CE向点E运动,当其中一个点到达后,另一个点也停止运动.设△APQ的面积为S,运动时间为t s,则S与t之间的函数关系的大致图象为( )
【分析】 由点Q从点N出发,沿折线ND-DC-CE向点E运动,确定出点Q分别在ND,DC,CE运动时对应的t的取值范围,再根据t所在的取值范围分别求出其对应的函数关系式,最后根据函数关系式确定对应的函数图象.
1.(2016·烟台)如图,⊙O的半径为1,AD,BC是⊙O的两条相互垂直的直径,点P从点O出发(P点与O点不重合),沿OCD的路线运动.设AP=x,sin∠APB=y,那么y与x之间的关系图象大致是( )
2.(2016·莱芜)如图,正方形ABCD的边长为3 cm,动点M从点B出发以3 cm/s的速度沿着边BC-CD-DA运动,到达点A停止运动;另一动点N同时从点B出发,以1 cm/s的速度沿着BA向点A运动,到达点A停止运动.设点M的运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
类型二 二次函数综合题
二次函数的综合题是中考数学的必考问题,一般作为压轴题出现,常与动点、存在点、相似等相结合,难度较大,是考生失分的重灾区.为攻克二次函数的压轴题,我们把二次函数大题拆分,逐步讲解,大题小做,稳拿分.
1.二次函数动点问题
(2017·泰安)如图,在△ABC中,∠C=90°,AB=10 cm,BC=8 cm,点P从点A沿AC向点C以1 cm/s的速度运动,同时点Q从点C沿CB向点B以2 cm/s的速度运动(点Q运动到点B停止),在运动过程中,四边形PABQ的面积最小值为( )
A.19 cm2 B.16 cm2
C.15 cm2 D.12 cm2
【分析】 首先利用勾股定理可得出AC的长,再设运动时间为t(0≤t≤4),利用分割图形求面积法可得出S四边形PABQ,利用配方法即可求出四边形PABQ的面积最小值.
3.(2017·新疆)如图,在边长为6 cm的正方形ABCD中,点E,F,G,H分别从点A,B,C,D同时出发,均以1 cm/s的速度向点B,C,D,A匀速运动,当点E到达点B时,四个点同时停止运动,在运动过程中,当运动时间为___ s时,四边形EFGH的面积最小,其最小值是______cm2.
4.(2016·德州)已知,m,n是一元二次方程x2+4x+3=0的两个实数根,且|m|<|n|,抛物线y=x2+bx+c的图象过点A(m,0),B(0,n),如图所示.
(1)求这个抛物线的表达式;
(2)点P是直线BC上的一个动点(点P不与点B和点C重合),过点P作x轴的垂线,交抛物线于点M,点Q在直线BC上,距离点P为个单位长度,设点P的横坐标为t,△PMQ的面积为S,求出S与t之间的函数关系式.
2.二次函数存在点问题
(2017·苏州)如图,二次函数y=x2+bx+c的图象与x轴交于Α,Β两点,与y轴交于点C,OB=OC.点D在函数图象上,CD∥x轴,且CD=2,直线l是抛物线的对称轴,E是抛物线的顶点.
(1)求b,c的值;
(2)如图1,连接BE,线段OC上的点F关于直线l的对称点F′恰好在线段BE上,求点F的坐标;
(3)如图2,动点Ρ在线段OB上,过点Ρ作x轴的垂线,分别与BC交于点M,与抛物线交于点N.试问:抛物线上是否存在点Q,使得△PQN与△APM的面积相等,且线段ΝQ的长度最小?若存在,求出点Q的坐标;若不存在,说明理由.
【分析】 (1)由条件可求得抛物线对称轴,则可求得b的值;由OB=OC,可用c表示出B点坐标,代入抛物线表达式可求得c的值;(2)可设F(0,m),则可表示出F′的坐标,由B,E的坐标可求得直线BE的表达式,把F′坐标代入直线BE表达式可得到关于m的方程,可求得F点的坐标;(3)设点P坐标为(n,0),可表示出PA,PB,PN的长,作QR⊥PN,垂足为R,则可求得QR的长,用n可表示出Q,R,N的坐标,在Rt△QRN中,由勾股定理可得到关于n的二次函数,利用二次函数的性质可知其取得最小值时n的值,则可求得Q点的坐标,
解决二次函数存在点问题,一般先假设该点存在,根据该点所在的直线或抛物线的表达式,设出该点的坐标;然后用该点的坐标表示出与该点有关的线段长或其他点的坐标等;最后结合题干中其他条件列出等式,求出该点的坐标,然后判别该点坐标是否符合题意,若符合题意,则该点存在,否则该点不存在.
5.(2016·日照)如图1,抛物线y=-[(x-2)2+n]与x轴交于点A(m-2,0)和B(2m+3,0)(点A在点B的左侧),与y轴交于点C,连接BC.
(1)求m,n的值;
(2)如图2,点M,P分别为线段BC和线段OB上的动点,连接PM,PC,是否存在这样的点P,使△PCM为等腰三角形、△PMB为直角三角形同时成立?若存在,求出点P的坐标;若不存在,请说明理由.
3.二次函数相似问题
(2017·日照)如图,在平面直角坐标系中,⊙C经过坐标原点O,且与x轴,y轴分别相交于M(4,0),N(0,3)两点.已知抛物线开口向上,与⊙C交于N,H,P三点,P为抛物线的顶点,抛物线的对称轴经过点C且垂直x轴于点D.
(1)求线段CD的长及顶点P的坐标;
(2)求抛物线的函数表达式;
(3)设抛物线交x轴于A,B两点,在抛物线上是否存在点Q,使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立?若存在,请求出Q点的坐标;若不存在,请说明理由.
【分析】 (1)由勾股定理可求得MN的长,在Rt△OCD中,可求得CD的长,则可求得P点坐标;(2)可设抛物线的表达式为顶点式,再把N点坐标代入可求得抛物线表达式;(3)由抛物线表达式可求得A,B的坐标,由S四边形OPMN=8S△QAB可求得点Q到x轴的距离,且点Q只能在x轴的下方,则可求得Q点的坐标,再证明△QAB∽△OBN即可.
二次函数相似问题常与动点、存在点相结合,利用动点或存在点的坐标表示出与相似三角形有关的线段长,要注意边的对应有多种可能,对每一种情况都要具体分析讨论,然后利用相似三角形的对应边成比例列出方程,通过解方程求得结果,还要考虑求出的结果是否符合题意及实际情况.
6.如图,已知抛物线经过原点O,顶点为A(1,1),且与直线y=x-2交于B,C两点,且AB⊥BC.
(1)求抛物线的表达式及点C的坐标;
(2)若点N为x轴上的一个动点,过点N作MN⊥x轴与抛物线交于点M,则是否存在以O,M,N为顶点的三角形与△ABC相似?若存在,请求出点N的坐标;若不存在,请说明理由.
参考答案
【聚焦泰安】
【例1】 如图,过点D作DF⊥AB于点F,过点Q作QG⊥AB于点G,
当0≤t≤2时,点Q在线段ND上.
∵AB∥CD,∠B=90°,∴四边形BCDF是矩形,
∴DF=BC=4,
∴AF==3,
∴DC=BF=2,
∴AQ=AN+NQ=3+t,AP=AM+MP=1+t.
∵QG∥DF,∴△AQG∽△ADF,
∴=,即=,∴QG=(3+t),
∴S=AP·QG=×(1+t)×(3+t)=t2+t+,且当t=2时,点Q恰好运动到点D,S=6;
当2<t≤4时,点Q在线段DC上,
∴S=AP·BC=×(1+t)×4=2t+2;
当4<t≤5时,点P,Q均在BC上运动,BP=CQ=t-4,
∴PQ=BC-BP-CQ=12-2t,
∴S=AB·PQ=×5×(12-2t)=-5t+30,且当t=5时,点Q运动到点E后停止运动,此时S=5.
综上所述,S=
由函数关系式,S与t之间的函数关系的大致图象为C或D.
∵t=2时,S=6;t=5时,S=5,6>5,
∴S与t之间的函数关系的大致图象为D.故选D.
变式训练 1.C 2.A
【例2】 在Rt△ABC中,∠C=90°,
AB=10 cm,BC=8 cm,
∴AC==6 cm.
设运动时间为t(0≤t≤4),
则PC=(6-t)cm,CQ=2t cm,
∴S四边形PABQ=S△ABC-S△CPQ=AC·BC-PC·CQ=×6×8-(6-t)×2t=t2-6t+24=(t-3)2+15,
∴当t=3时,四边形PABQ的面积取最小值,最小值为15.故选C.
变式训练3.3 18
4.解:(1)解方程x2+4x+3=0得x1=-1,x2=-3.
∵m,n是方程x2+4x+3=0的两根,且|m|<|n|,
∴m=-1,n=-3.
把点A(-1,0),B(0,-3)代入y=x2+bx+c,
得
解得
∴这个抛物线的表达式为y=x2-2x-3.
(2)由B(0,-3),C(3,0),得直线BC的表达式为y=x-3.
∴设点P的坐标为(t,t-3).
∵PM⊥x轴,点M在抛物线上,
∴点M的坐标为(t,t2-2t-3).
如图,过点Q作QF⊥PM于点F,则△PQF为等腰直角三角形.
∵PQ=,∴QF=1.
如图,当点P在点M上方时,即0<t<3.
PM=(t-3)-(t2-2t-3)=-t2+3t,
∴S=PM·QF=(-t2+3t)=-t2+t.
如图,当点P在点M下方时,即t<0或t>3.
PM=(t2-2t-3)-(t-3)=t2-3t,
∴S=PM·QF=(t2-3t)=t2-t.
综上所述,S=
【例3】 (1)∵CD∥x轴,CD=2,
∴抛物线对称轴为直线l:x=1.
∴-=1,∴b=-2.
∵OB=OC,C(0,c),∴B点的坐标为(-c,0),
∵点B在抛物线上,
∴0=c2+2c+c,解得c=-3或c=0(舍去),∴c=-3.
(2)设点F的坐标为(0,m).
∵对称轴为直线l:x=1,
∴点F关于直线l的对称点F的坐标为(2,m).
∵直线BE经过点B(3,0),E(1,-4),
∴利用待定系数法可得直线BE的表达式为y=2x-6.
∵点F在BE上,
∴m=2×2-6=-2,即点F的坐标为(0,-2).
(3)存在点Q满足题意.
设点P坐标为(n,0),
则PA=n+1,PB=PM=3-n,PN=-n2+2n+3.
如图,作QR⊥PN,垂足为R,
∵S△PQN=S△APM,
∴(n+1)(3-n)=(-n2+2n+3)·QR,∴QR=1.
①点Q在直线PN的左侧时,Q点的坐标为(n-1,n2-4n),R点的坐标为(n,n2-4n),N点的坐标为(n,n2-2n-3).在Rt△QRN中,NQ2=1+(2n-3)2,
∴n=时,NQ取最小值1.此时Q点的坐标为(,-).
②点Q在直线PN的右侧时,Q点的坐标为(n+1,n2-4).同理,NQ2=1+(2n-1)2,
∴n=时,NQ取最小值1.此时Q点的坐标为(,-).
综上所述,满足题意的点Q的坐标为(,-)和(,-).
变式训练
5.解:(1)∵抛物线的对称轴是x=2,
∴m-2+2m+3=4,解得m=1,
∴A(-1,0), B(5,0).
把A(-1,0)代入抛物线表达式,
得-(9+n)=0,解得n=-9,
∴m=1,n=-9.
(2)假设点P存在,设点P(x0,0)(0
∵MP∥OC,∴=,=,
∴MP=(5-x0),CM=x0.
则(5-x0)=x0,解得x0=,
∴P(,0).
②当点M为△PMB的直角顶点时,则 CM=MP.
∵△PMB∽△COB,∴==,
∴PM=(5-x0),BM=(5-x0),
∴CM=-(5-x0)=.
则(5-x0)=,解得x0=,∴P(,0).
综上所述,满足条件的点P的坐标为(,0)或(,0).
【例4】 (1)∵O,M,N三点都在⊙C上,
且∠MON=90°,
∴MN为⊙C的直径,点C为MN的中点.
∵M(4,0),N(0,3),∴C(2,1.5),
MN==5,
∴CP=2.5,∴CD=1.5,顶点P的坐标为(2,-1).
(2)∵抛物线的顶点坐标为P(2,-1),
∴可设抛物线的表达式为y=a(x-2)2-1.
又∵抛物线过点N(0,3),∴3=4a-1,解得a=1,
故抛物线的表达式为y=(x-2)2-1=x2-4x+3.
(3)由题意得:
S四边形OPMN=S△OMN+S△OPM=×4×3+×4×1=8.
∵S四边形OPMN=8S△QAB,∴S△QAB=1.
当y=0时,x2-4x+3=0,
解得x=1或x=3,
∴A(1,0),B(3,0).
设Q(x,y),则S△QAB=|AB|·|y|=|y|=1.
∵△OBN为等腰直角三角形,且△QAB∽△OBN,
∴△QAB也应为等腰直角三角形.
当y=1时,结合图形易知,△QAB一定不是直角三角形,不合题意;
当y=-1时,点Q的坐标为(2,-1),
此时QA=QB=,AB=2,
∴△QAB为等腰直角三角形,符合题意.
综上可知,存在点Q(2,-1),使得S四边形OPMN=8S△QAB,且△QAB∽△OBN成立.
变式训练
6.解:(1)∵顶点A的坐标为(1,1),
∴设抛物线的表达式为y=a(x-1)2+1.
∵抛物线过原点,∴0=a(0-1)2+1,解得a=-1.
∴抛物线的表达式为y=-(x-1)2+1,
即y=-x2+2x.
令y=-x2+2x=x-2,解得x=2或x=-1.
当x=2时,y=2-2=0,即B(2,0).
当x=-1时,y=-1-2=-3,即C(-1,-3).
(2)假设存在满足条件的点N,
设N(x,0),则M (x,-x2+2x),
∴ON=|x|,MN=|-x2+2x|.
由A(1,1),B(2,0),C(-1,-3),
得AB=,BC=3.
∵AB⊥BC,MN⊥x轴于点N,
∴∠ABC=∠MNO=90°,
∴当△MNO∽△ABC时,有=,
即= ,
整理得|x|·|-x+2|=|x|.
当x=0时,M,O,N不能构成三角形,故x≠0.
∴|-x+2|=,解得x=或x=.
此时点N的坐标为(,0)或(,0).
当△ONM∽△ABC时,有=,
即=,
整理得|x|·|-x+2|=3|x|.
∵x≠0,∴|-x+2|=3,解得x=5或x=-1.
此时点N的坐标为(-1,0)或(5,0).
综上所述,存在满足条件的N点,其坐标为(,0)或(,0)或(-1,0)或(5,0).
同课章节目录
