17.1.3 勾股定理的应用课件
图片预览




文档简介
(共17张PPT)
17.1.3 勾股定理的应用
人教版 八年级下
1、设直角三角形的两条直角边长分别为a、b,
斜边长为c。
⑴ 已知a=6,b=8,则斜边c= ;
解:由勾股定理,得
6
8
c2=a2+b2
=62+82
=100
c=10
10
1、设直角三角形的两条直角边长分别为a、b,
斜边长为c。
⑵ 已知a=5,b=12,则斜边c= ;
解:由勾股定理,得
5
12
c2=a2+b2
=52+122
=169
c=13
13
1、设直角三角形的两条直角边长分别为a、b,
斜边长为c。
⑶ 已知c=25,b=15,则直角边a= ;
解:由勾股定理,得
?
15
25
a2=c2-b2
=252-152
=400
a=20
20
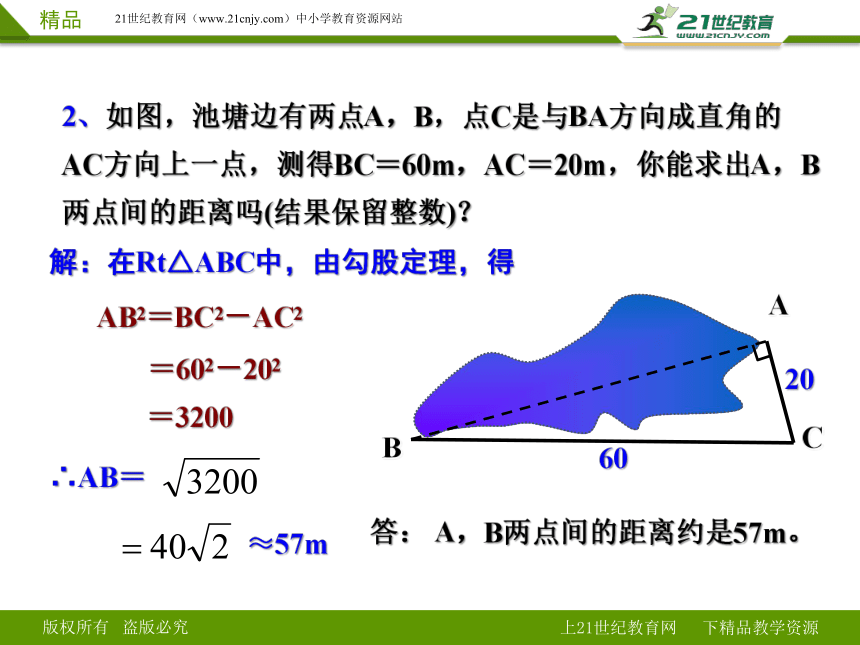
2、如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,你能求出A,B两点间的距离吗(结果保留整数)?
A
B
C
20
60
解:在Rt△ABC中,由勾股定理,得
AB2=BC2-AC2
=602-202
=3200
∴AB=
≈57m
答: A,B两点间的距离约是57m。
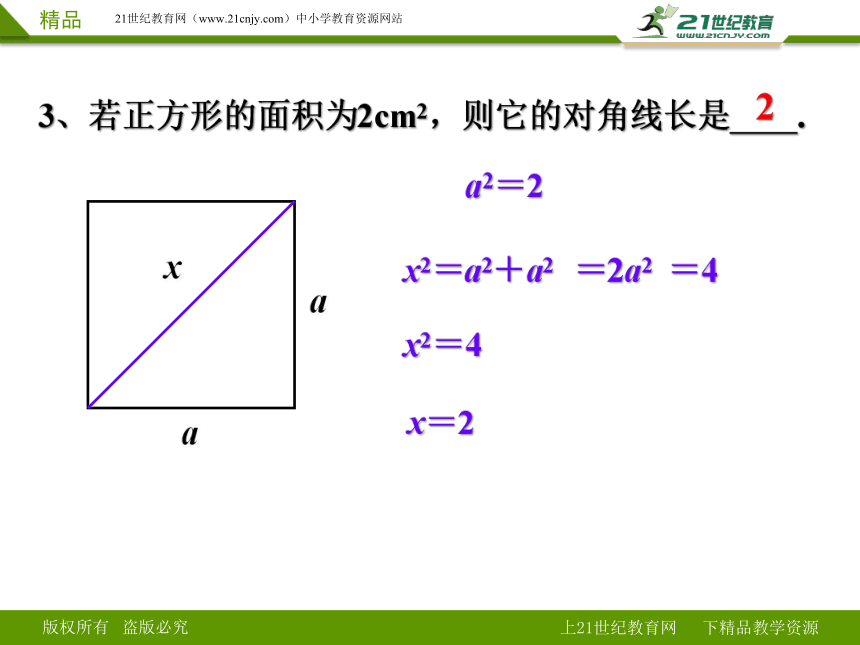
3、若正方形的面积为2cm2,则它的对角线长是 .
x
a
a
a2=2
x2=a2+a2
=2a2
=4
x2=4
x=2
2
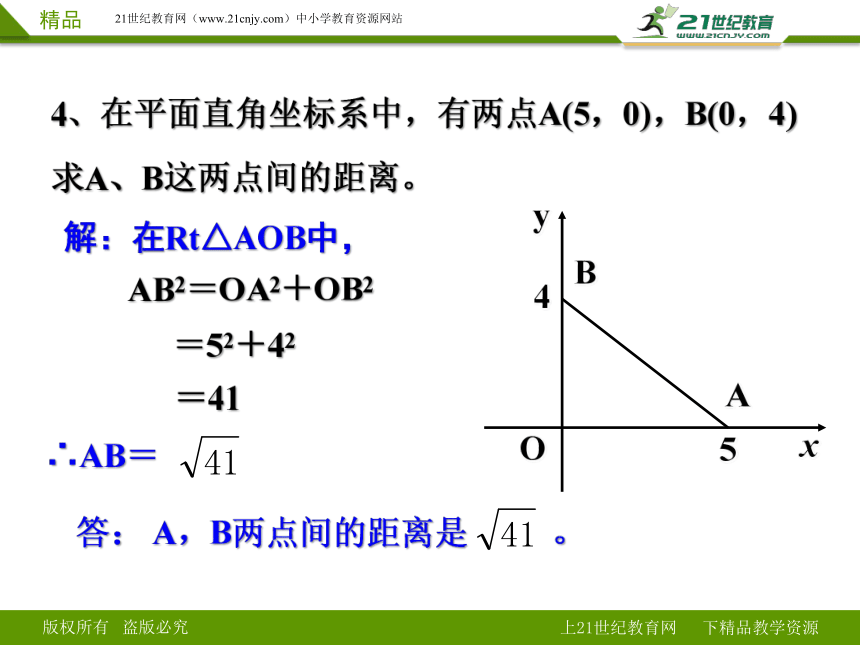
4、在平面直角坐标系中,有两点A(5,0),B(0,4)
求A、B这两点间的距离。
解:在Rt△AOB中,
AB2=OA2+OB2
=52+42
=41
∴AB=
答: A,B两点间的距离是 。
A
B
x
O
4
5
y
5、 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .
6、8、10
解:设三边分别为a-2、 a、 a+2。
(a-2)2+a2= (a+2)2
a2-8a=0
a=0或a=8
三边分别为6、8、10
a(a-8) =0
6、如图所示,在P港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里的速度前进,乙船沿南偏东30°方向以每小时15海里的速度前进,两小时后,甲船到达A岛,乙船到达B岛,求A、B两岛之间的距离。
A
B
P
北
东
60°
30°
解:由题意可知∠APB=90°
AP=8×2=16 (海里)
BP=15×2=30 (海里)
AB2=AP2+BP2
=162+302
=1156
∴AB=
=34(海里)
答:A、B两岛之间的距离为34海里。
7、有一个边长为50cm的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50
50
解:在Rt△ABC中,
A
B
C
AB2=BC2+AC2
=502+502
=5000
∴AB=
≈71cm
答:圆的直径至少71cm。
8、一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
A
B
C
D
2m
1m
分析:可以看到,木板横着进,竖着进,都不能从门框内通过,只能试试斜着能否通过。对角线AC是斜着能通过的最大长度。求出AC,再与木板的宽比较,就能知道木板能否通过。
8、一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
解:在Rt△ABC中,
AC2=AB2+BC2
=12+22
=5
∴AC=
≈2.236
∵AC>木板的宽
A
B
C
D
2m
1m
∴木板能从门框内通过。
9、如图,一个2.6m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.4m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
A
B
C
D
O
解:在Rt△AOB中,
OB2=AB2-AO2
=2.62-2.42
=1
∴ OB=1
在Rt△COD中,
OD2=CD2-CO2
=2.62-(2.4-0.5)2
=3.15
∴ OD≈1.77 (用计算器算出)
BD=OD-OB
=0.77
答:梯子底端B外移0.77m
10、甲、乙两位探险者到沙漠进行探险,用完了所带的水,需要寻找水源。为了不至于走散,他们用两部对讲机联系,已知对讲机的有效距离为15千米,早晨8:00甲先出发,他以 6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00甲、乙两人相距多远?他们还能保持联系吗?为什么?
10、甲、乙两位探险者到沙漠进行探险,用完了所带的水,需要寻找水源。为了不至于走散,他们用两部对讲机联系,已知对讲机的有效距离为15千米,早晨8:00甲先出发,他以 6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00甲、乙两人相距多远?他们还能保持联系吗?为什么?
北
东
O
A
B
解:在Rt△AOB中,
OA=6×2=12km
OB=5×1=5km
AB2=OA2+OB2
=122+52
=169
∴AB=13km<15km
答:上午10:00甲、乙相距13千米,
他们能保持联系。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
17.1.3 勾股定理的应用
人教版 八年级下
1、设直角三角形的两条直角边长分别为a、b,
斜边长为c。
⑴ 已知a=6,b=8,则斜边c= ;
解:由勾股定理,得
6
8
c2=a2+b2
=62+82
=100
c=10
10
1、设直角三角形的两条直角边长分别为a、b,
斜边长为c。
⑵ 已知a=5,b=12,则斜边c= ;
解:由勾股定理,得
5
12
c2=a2+b2
=52+122
=169
c=13
13
1、设直角三角形的两条直角边长分别为a、b,
斜边长为c。
⑶ 已知c=25,b=15,则直角边a= ;
解:由勾股定理,得
?
15
25
a2=c2-b2
=252-152
=400
a=20
20
2、如图,池塘边有两点A,B,点C是与BA方向成直角的AC方向上一点,测得BC=60m,AC=20m,你能求出A,B两点间的距离吗(结果保留整数)?
A
B
C
20
60
解:在Rt△ABC中,由勾股定理,得
AB2=BC2-AC2
=602-202
=3200
∴AB=
≈57m
答: A,B两点间的距离约是57m。
3、若正方形的面积为2cm2,则它的对角线长是 .
x
a
a
a2=2
x2=a2+a2
=2a2
=4
x2=4
x=2
2
4、在平面直角坐标系中,有两点A(5,0),B(0,4)
求A、B这两点间的距离。
解:在Rt△AOB中,
AB2=OA2+OB2
=52+42
=41
∴AB=
答: A,B两点间的距离是 。
A
B
x
O
4
5
y
5、 一个直角三角形的三边为三个连续偶数,则它的三边长分别为 .
6、8、10
解:设三边分别为a-2、 a、 a+2。
(a-2)2+a2= (a+2)2
a2-8a=0
a=0或a=8
三边分别为6、8、10
a(a-8) =0
6、如图所示,在P港有甲、乙两艘渔船,若甲船沿北偏东60°方向以每小时8海里的速度前进,乙船沿南偏东30°方向以每小时15海里的速度前进,两小时后,甲船到达A岛,乙船到达B岛,求A、B两岛之间的距离。
A
B
P
北
东
60°
30°
解:由题意可知∠APB=90°
AP=8×2=16 (海里)
BP=15×2=30 (海里)
AB2=AP2+BP2
=162+302
=1156
∴AB=
=34(海里)
答:A、B两岛之间的距离为34海里。
7、有一个边长为50cm的正方形洞口,想用一个圆盖去盖住这个洞口,圆的直径至少多长?(结果保留整数)
50
50
解:在Rt△ABC中,
A
B
C
AB2=BC2+AC2
=502+502
=5000
∴AB=
≈71cm
答:圆的直径至少71cm。
8、一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
A
B
C
D
2m
1m
分析:可以看到,木板横着进,竖着进,都不能从门框内通过,只能试试斜着能否通过。对角线AC是斜着能通过的最大长度。求出AC,再与木板的宽比较,就能知道木板能否通过。
8、一个门框的尺寸如图所示,一块长3m,宽2.2m的薄木板能否从门框内通过?为什么?
解:在Rt△ABC中,
AC2=AB2+BC2
=12+22
=5
∴AC=
≈2.236
∵AC>木板的宽
A
B
C
D
2m
1m
∴木板能从门框内通过。
9、如图,一个2.6m长的梯子AB,斜靠在一竖直的墙AO上,这时AO的距离为2.4m,如果梯子的顶端A沿墙下滑0.5m,那么梯子底端B也外移0.5m吗?
A
B
C
D
O
解:在Rt△AOB中,
OB2=AB2-AO2
=2.62-2.42
=1
∴ OB=1
在Rt△COD中,
OD2=CD2-CO2
=2.62-(2.4-0.5)2
=3.15
∴ OD≈1.77 (用计算器算出)
BD=OD-OB
=0.77
答:梯子底端B外移0.77m
10、甲、乙两位探险者到沙漠进行探险,用完了所带的水,需要寻找水源。为了不至于走散,他们用两部对讲机联系,已知对讲机的有效距离为15千米,早晨8:00甲先出发,他以 6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00甲、乙两人相距多远?他们还能保持联系吗?为什么?
10、甲、乙两位探险者到沙漠进行探险,用完了所带的水,需要寻找水源。为了不至于走散,他们用两部对讲机联系,已知对讲机的有效距离为15千米,早晨8:00甲先出发,他以 6千米/时的速度向东行走,1小时后乙出发,他以5千米/时的速度向北行进,上午10:00甲、乙两人相距多远?他们还能保持联系吗?为什么?
北
东
O
A
B
解:在Rt△AOB中,
OA=6×2=12km
OB=5×1=5km
AB2=OA2+OB2
=122+52
=169
∴AB=13km<15km
答:上午10:00甲、乙相距13千米,
他们能保持联系。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
