17.1.2 勾股定理的证明与练习课件
图片预览







文档简介
(共32张PPT)
17.1.2勾股定理的证明与练习
人教版 八年级下
一、勾股定理的证明
两千多年来,人们对勾股定理的证明颇感兴趣。因为这个定理太贴近人们的生活实际,以至于古往今来,下至平民百姓,上至帝王总统都愿意探讨、研究它的证明,因此不断出现新的证法。下面介绍几种证明勾股定理的图形,你能根据这些图形及提示证明勾股定理吗?
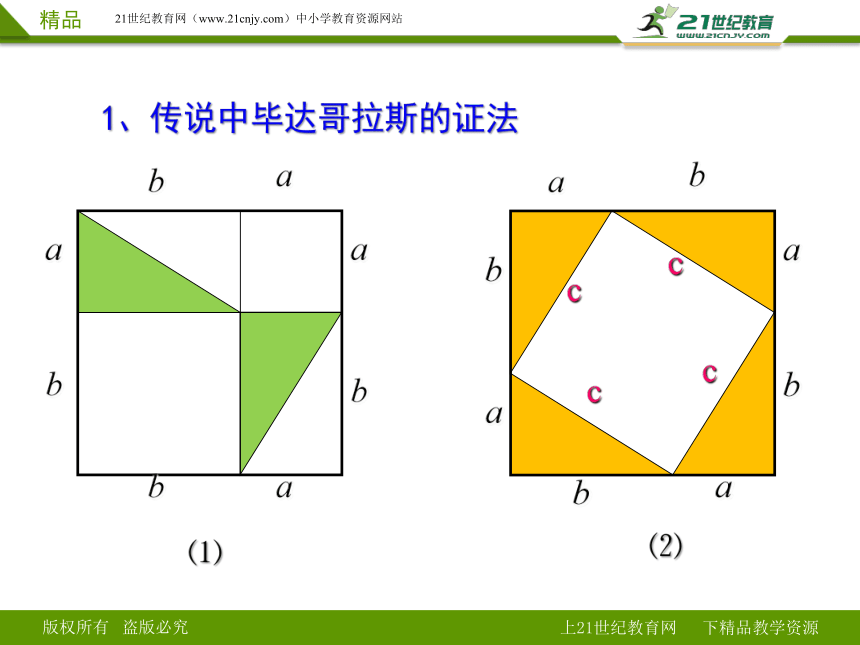
1、传说中毕达哥拉斯的证法
a
b
b
a
a
b
b
a
a
b
a
b
a
b
a
b
c
c
c
c
⑴
⑵
a
b
b
a
a
b
b
a
a
b
a
b
a
b
a
b
c
c
c
c
⑴
⑵
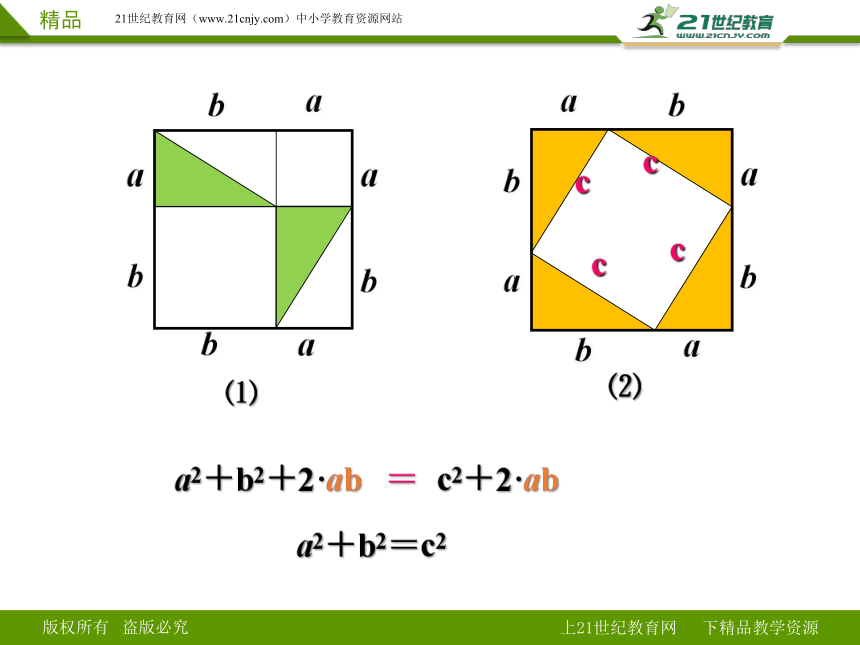
a2+b2+2·ab
c2+2·ab
=
a2+b2=c2
2、弦图的另一种证法
①大正方形的面积∶
②四个直角三角形的面积加上一个小正方形的面积∶
a
a
a
a
b
b
b
b
c
c
c
c
上图的面积可用两种方法来表示
(a+b)
(a+b) =2ab+c2
a2+b2=c2
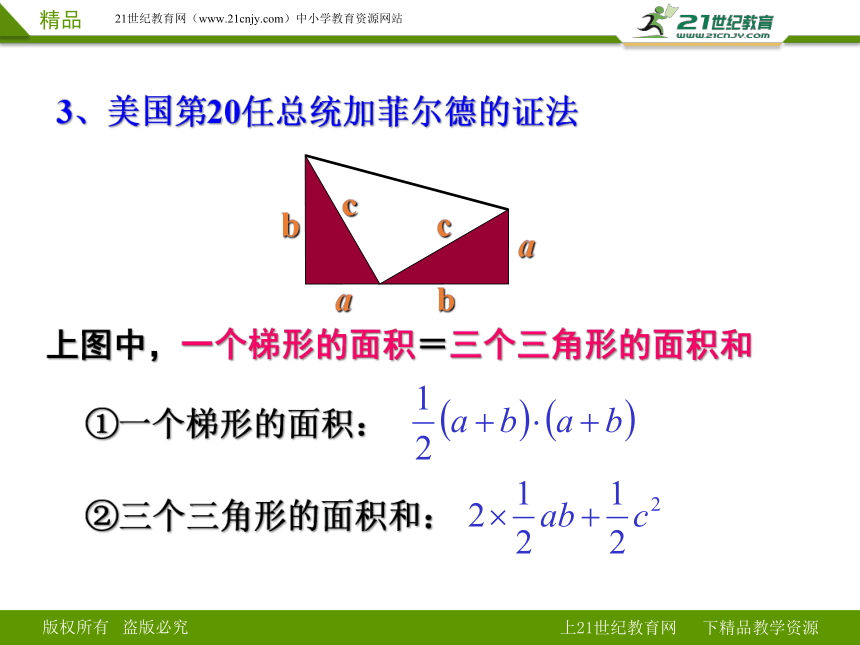
3、美国第20任总统加菲尔德的证法
②三个三角形的面积和:
①一个梯形的面积:
a
a
b
b
c
c
上图中,一个梯形的面积=三个三角形的面积和
②三个三角形的面积和:
①一个梯形的面积:
上图中,一个梯形的面积=三个三角形的面积和
(a+b) =2ab+c2
a
a
b
b
c
c
a2+b2=c2
a
b
c
b
a
c
(1)
(2)
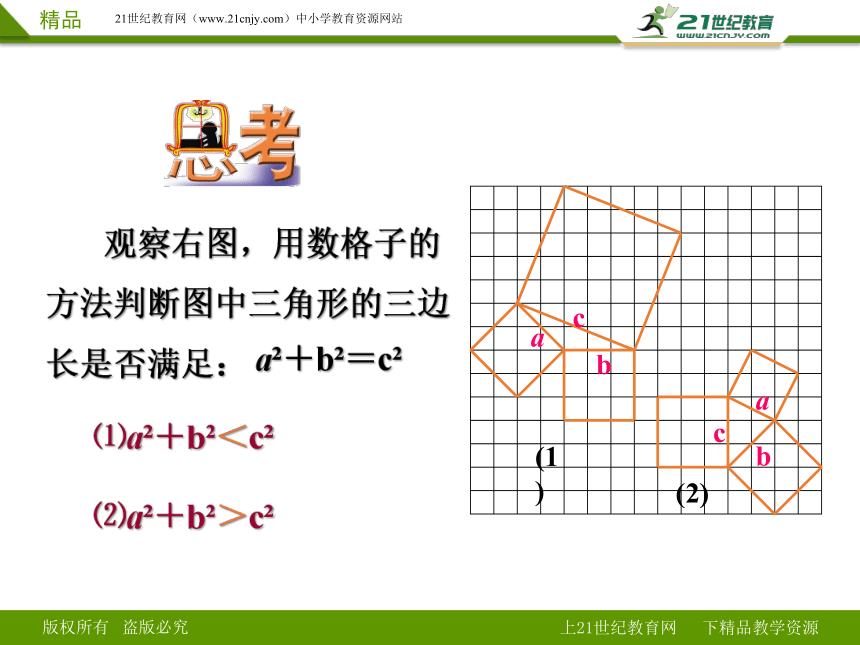
观察右图,用数格子的方法判断图中三角形的三边长是否满足:
a +b =c
⑴a +b <c
⑵a +b >c
勾股定理的推广
(Ⅰ)在锐角△ABC中,边c是最长边,则
(Ⅱ)在钝角△ABC中,边c是最长边,则
c >a +b
c <a +b
⑵、在Rt ABC中,AB=5,AC=12,
则斜边BC=13 . 〖 〗
1、判断题
⑴、在Rt ABC中,a=6,b=8,则c=10. 〖 〗
边c不一定是最长边
② 若c=10,a∶b=3∶4,
则a= ,b= .
⑴、在 ABC中,∠C=90°,
6
8
2、填空题
① 若a=9,b=40,则c=______.
41
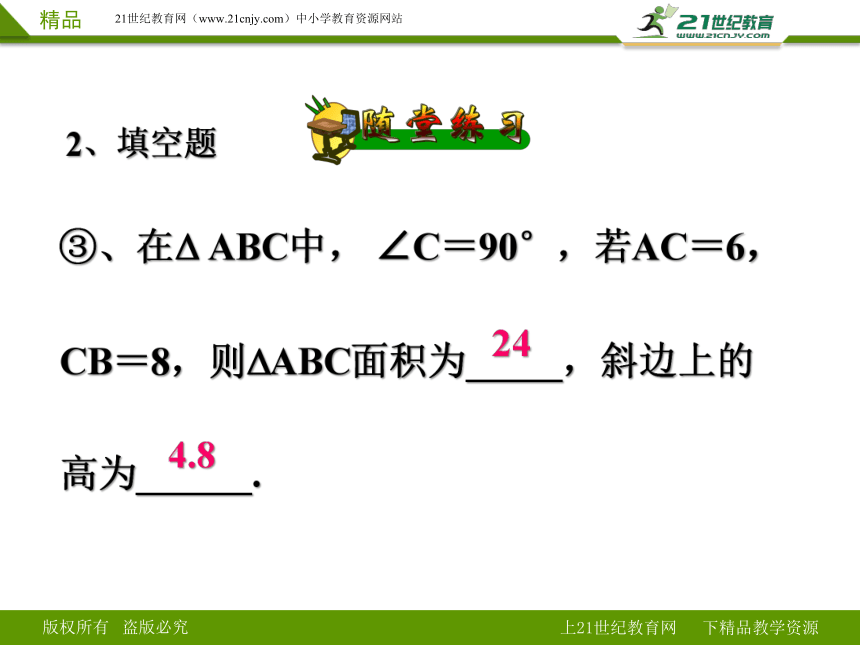
③、在 ABC中, ∠C=90°,若AC=6,CB=8,则 ABC面积为_____,斜边上的高为______.
24
4.8
2、填空题
【问题1】 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
问题 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
解:由于 22+32=13
∴ 只要画出两直角边分别为2和3的直角三角形,则其斜边就是
0
1
2
3
4
5
【问题2 】 在数轴上,你能画出任意正整数的算术平方根表示的数吗?
0
1
回答是肯定的!
利用勾股定理,可以作出长为
·······的线段。
1
1
1
1
1
1
1
1
利用勾股定理,可以作出长为
·······的线段。
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
3、在数轴上作出表示 的点。
解:由于 42+12=17
∴ 只要画出两直角边分别为4和1的直角三角形,则其斜边就是
0
1
2
3
4
5
4、如图,等边三角形的边长是6.
⑴ 求高AD的长 (结果保留3位小数)
⑵ 求这个三角形的面积
(结果保留1位小数)
A
B
C
D
解:⑴ 在Rt△ABD中,
AD2=AB2-BD2
=62-32
=27
≈5.196
4、如图,等边三角形的边长是6:
⑴ 求高AD的长 (结果保留3位小数)
⑵ 求这个三角形的面积 (结果保留1位小数)
A
B
C
D
⑵ S△ABC=
≈15.6
5、求下图中字母所代表的正方形的面积。
225
A
400
225
B
81
⑴ SA=625
⑵ SB=144
6、求出下列直角三角形中未知边的长度。
6
8
x
5
13
y
解:x2=62+82
=100
∴ x=10
解:y2=132-52
=144
∴ y=12
7、如图,一棵树在离地面9米处断裂,树的顶部落在离底部12米处,这棵树断裂前有多高?
9米
12米
A
B
C
解:在Rt△ABC中,
AB2=AC2+BC2
=92+122
=225
AB=15
AB+BC=24(米)
答:这棵树折断前有24米高。
8、求斜边长17厘米,一条直角边长为15厘米的直角三角形
的面积。
17
15
解:设另一条直角边为x厘米,
根据勾股定理得;
x2 = 172-152
=289—225
=64
x =8
S△=8×15÷2
=60cm2
8
9、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物的距离AB为6米,为此至少需要多长的梯子?
8m
6m
A
B
答:梯子至少长10米。
C
解:根据勾股定理得
AC2= 62+ 82
=36+64
=100
AC=10
10、如图,在△ABC中,∠ACB=90。,CD是高,
若AB=13cm,AC=5cm,求CD的长;
A
B
C
D
解:在Rt△ABC中,
BC2=AB2-AC2
=132-52
=144
5
13
BC=12
S△ABC = 12×5÷2
12
=30cm2
S△ABC = 12×5÷2
=30cm2
13·CD÷2 =30
(cm)
答:CD的长是 cm.
A
B
C
D
5
13
12
10、如图,在△ABC中,∠ACB=90。,CD是高,
若AB=13cm,AC=5cm,求CD的长;
11、下图阴影部分是一个正方形,求此正方形的面积。
15厘米
17厘米
解:S=172-152
=64厘米2
12、如图,从电线杆离地面6米处向地面拉一条长10米的缆绳,这条缆绳在地面的固定点距离电线杆底部有多远?
6米
10米
解:x2=102-62 =64
∴ x=8
答:有8米远。
13、飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?
4000米
5000米
A
B
C
解:在Rt△ABC中,
BC2=AB2-AC2
=50002-40002
=30002
BC=3000
v=3000÷20=150(米/秒)
=540(千米/时)
答:飞机每时飞行540千米.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
17.1.2勾股定理的证明与练习
人教版 八年级下
一、勾股定理的证明
两千多年来,人们对勾股定理的证明颇感兴趣。因为这个定理太贴近人们的生活实际,以至于古往今来,下至平民百姓,上至帝王总统都愿意探讨、研究它的证明,因此不断出现新的证法。下面介绍几种证明勾股定理的图形,你能根据这些图形及提示证明勾股定理吗?
1、传说中毕达哥拉斯的证法
a
b
b
a
a
b
b
a
a
b
a
b
a
b
a
b
c
c
c
c
⑴
⑵
a
b
b
a
a
b
b
a
a
b
a
b
a
b
a
b
c
c
c
c
⑴
⑵
a2+b2+2·ab
c2+2·ab
=
a2+b2=c2
2、弦图的另一种证法
①大正方形的面积∶
②四个直角三角形的面积加上一个小正方形的面积∶
a
a
a
a
b
b
b
b
c
c
c
c
上图的面积可用两种方法来表示
(a+b)
(a+b) =2ab+c2
a2+b2=c2
3、美国第20任总统加菲尔德的证法
②三个三角形的面积和:
①一个梯形的面积:
a
a
b
b
c
c
上图中,一个梯形的面积=三个三角形的面积和
②三个三角形的面积和:
①一个梯形的面积:
上图中,一个梯形的面积=三个三角形的面积和
(a+b) =2ab+c2
a
a
b
b
c
c
a2+b2=c2
a
b
c
b
a
c
(1)
(2)
观察右图,用数格子的方法判断图中三角形的三边长是否满足:
a +b =c
⑴a +b <c
⑵a +b >c
勾股定理的推广
(Ⅰ)在锐角△ABC中,边c是最长边,则
(Ⅱ)在钝角△ABC中,边c是最长边,则
c >a +b
c <a +b
⑵、在Rt ABC中,AB=5,AC=12,
则斜边BC=13 . 〖 〗
1、判断题
⑴、在Rt ABC中,a=6,b=8,则c=10. 〖 〗
边c不一定是最长边
② 若c=10,a∶b=3∶4,
则a= ,b= .
⑴、在 ABC中,∠C=90°,
6
8
2、填空题
① 若a=9,b=40,则c=______.
41
③、在 ABC中, ∠C=90°,若AC=6,CB=8,则 ABC面积为_____,斜边上的高为______.
24
4.8
2、填空题
【问题1】 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
问题 我们知道数轴上的点有的表示有理数,有的表示无理数,你能在数轴上画出表示 的点吗?
解:由于 22+32=13
∴ 只要画出两直角边分别为2和3的直角三角形,则其斜边就是
0
1
2
3
4
5
【问题2 】 在数轴上,你能画出任意正整数的算术平方根表示的数吗?
0
1
回答是肯定的!
利用勾股定理,可以作出长为
·······的线段。
1
1
1
1
1
1
1
1
利用勾股定理,可以作出长为
·······的线段。
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
1
3、在数轴上作出表示 的点。
解:由于 42+12=17
∴ 只要画出两直角边分别为4和1的直角三角形,则其斜边就是
0
1
2
3
4
5
4、如图,等边三角形的边长是6.
⑴ 求高AD的长 (结果保留3位小数)
⑵ 求这个三角形的面积
(结果保留1位小数)
A
B
C
D
解:⑴ 在Rt△ABD中,
AD2=AB2-BD2
=62-32
=27
≈5.196
4、如图,等边三角形的边长是6:
⑴ 求高AD的长 (结果保留3位小数)
⑵ 求这个三角形的面积 (结果保留1位小数)
A
B
C
D
⑵ S△ABC=
≈15.6
5、求下图中字母所代表的正方形的面积。
225
A
400
225
B
81
⑴ SA=625
⑵ SB=144
6、求出下列直角三角形中未知边的长度。
6
8
x
5
13
y
解:x2=62+82
=100
∴ x=10
解:y2=132-52
=144
∴ y=12
7、如图,一棵树在离地面9米处断裂,树的顶部落在离底部12米处,这棵树断裂前有多高?
9米
12米
A
B
C
解:在Rt△ABC中,
AB2=AC2+BC2
=92+122
=225
AB=15
AB+BC=24(米)
答:这棵树折断前有24米高。
8、求斜边长17厘米,一条直角边长为15厘米的直角三角形
的面积。
17
15
解:设另一条直角边为x厘米,
根据勾股定理得;
x2 = 172-152
=289—225
=64
x =8
S△=8×15÷2
=60cm2
8
9、如图,要登上8米高的建筑物BC,为了安全需要,需使梯子底端离建筑物的距离AB为6米,为此至少需要多长的梯子?
8m
6m
A
B
答:梯子至少长10米。
C
解:根据勾股定理得
AC2= 62+ 82
=36+64
=100
AC=10
10、如图,在△ABC中,∠ACB=90。,CD是高,
若AB=13cm,AC=5cm,求CD的长;
A
B
C
D
解:在Rt△ABC中,
BC2=AB2-AC2
=132-52
=144
5
13
BC=12
S△ABC = 12×5÷2
12
=30cm2
S△ABC = 12×5÷2
=30cm2
13·CD÷2 =30
(cm)
答:CD的长是 cm.
A
B
C
D
5
13
12
10、如图,在△ABC中,∠ACB=90。,CD是高,
若AB=13cm,AC=5cm,求CD的长;
11、下图阴影部分是一个正方形,求此正方形的面积。
15厘米
17厘米
解:S=172-152
=64厘米2
12、如图,从电线杆离地面6米处向地面拉一条长10米的缆绳,这条缆绳在地面的固定点距离电线杆底部有多远?
6米
10米
解:x2=102-62 =64
∴ x=8
答:有8米远。
13、飞机在空中水平飞行,某一时刻刚好飞到一个男孩头顶上方4000米处,过了20秒,飞机距离这个男孩头顶5000米。飞机每时飞行多少千米?
4000米
5000米
A
B
C
解:在Rt△ABC中,
BC2=AB2-AC2
=50002-40002
=30002
BC=3000
v=3000÷20=150(米/秒)
=540(千米/时)
答:飞机每时飞行540千米.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
