17.2 勾股定理的逆定理课件
图片预览









文档简介
(共44张PPT)
17.2 勾股定理的逆定理
人教版 八年级下
勾股定理(gou-gu theorem)
即如果直角三角形两直角边分别为a、b,斜边为c,
那么 a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方。
a
b
c
古代埃及,由于尼罗河的泛滥,给人民的生活带来极大的困难,由于需要多次地对土地进行丈量,却由此产生了数学文明。
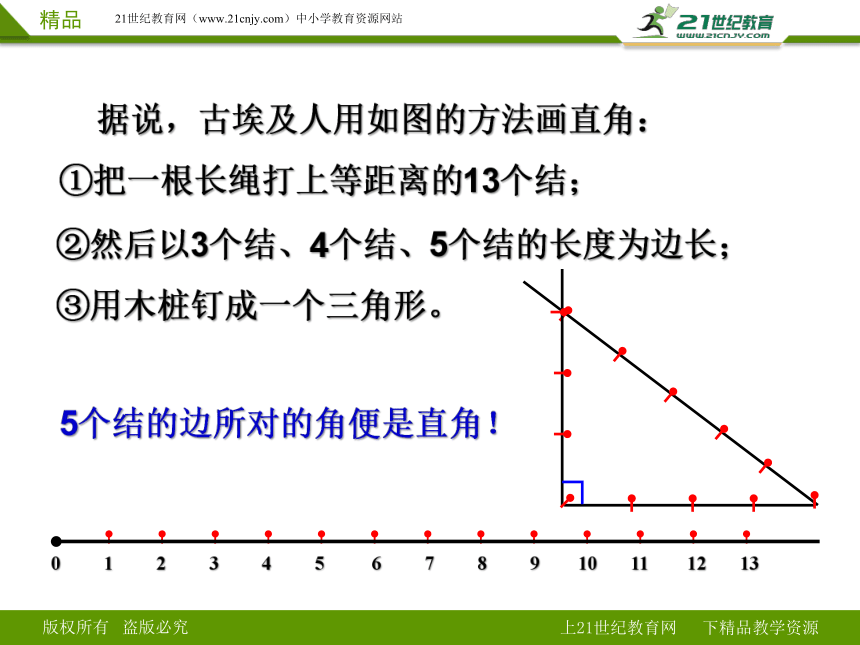
据说,古埃及人用如图的方法画直角:
①把一根长绳打上等距离的13个结;
②然后以3个结、4个结、5个结的长度为边长;
③用木桩钉成一个三角形。
5个结的边所对的角便是直角!
0 1 2 3 4 5 6 7 8 9 10 11 12 13
0 1 2 3 4 5 6 7 8 9 10 11 12 13
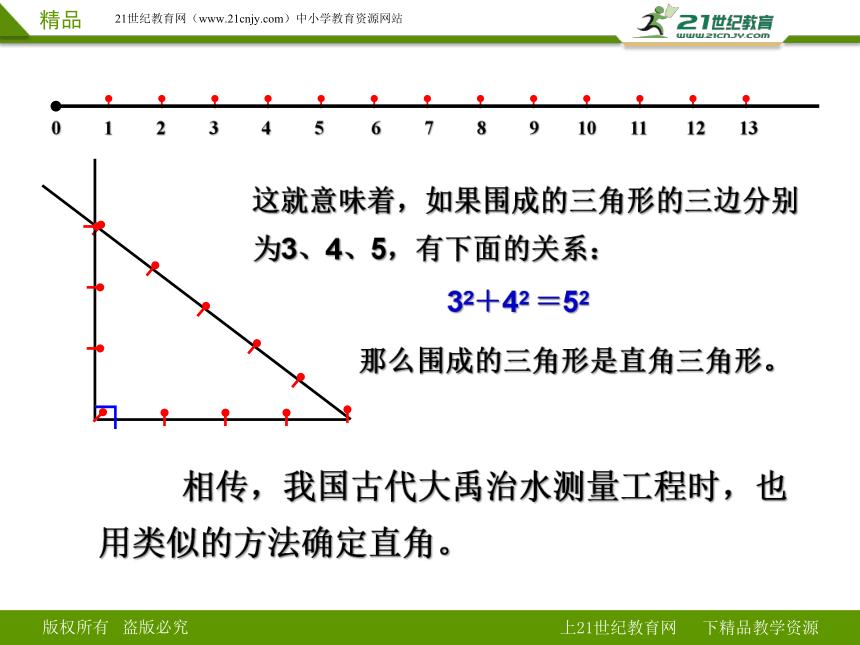
这就意味着,如果围成的三角形的三边分别为3、4、5,有下面的关系:
32+42 =52
那么围成的三角形是直角三角形。
相传,我国古代大禹治水测量工程时,也用类似的方法确定直角。
画出三边长分别为下面各组数的三角形,度量一下它们是直角三角形吗?
⑴ 2.5cm、6cm、6.5cm;
操作与探究
⑵ 4cm、7.5cm、8.5cm;
⑶ 5cm、6cm、7cm.
画出三边长分别为下面各组数的三角形,度量一下它们是直角三角形吗?
⑴ 2.5cm、6cm、6.5cm;
操作与探究
画出三边长分别为下面各组数的三角形,度量一下它们是直角三角形吗?
⑵ 4cm、7.5cm、8.5cm;
操作与探究
画出三边长分别为下面各组数的三角形,度量一下它们是直角三角形吗?
⑶ 5cm、6cm、7cm.
操作与探究
A
B
C
b
c
a
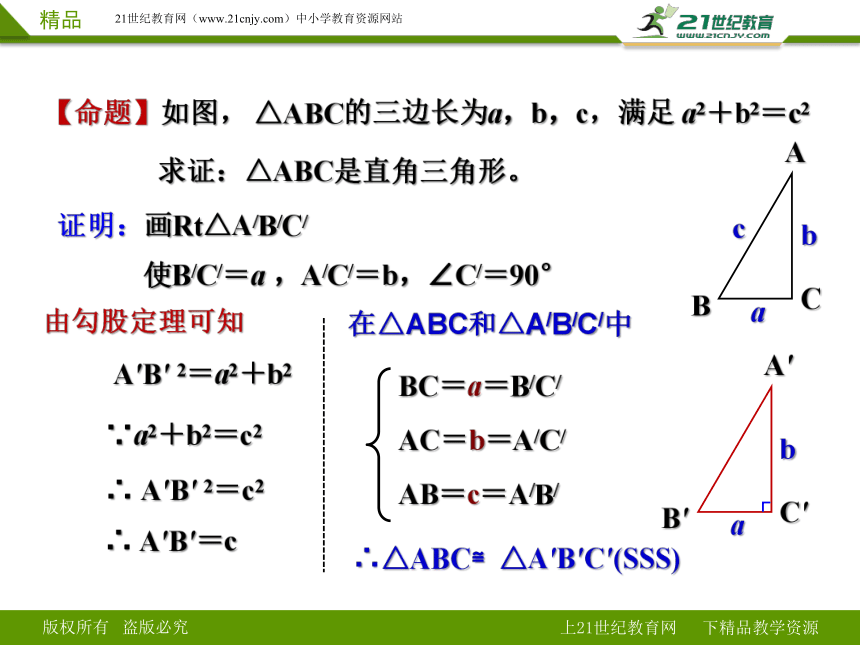
【命题】如图, △ABC的三边长为a,b,c,满足 a2+b2=c2
求证:△ABC是直角三角形。
证明:画Rt△A/B/C/
使B/C/=a ,A/C/=b,∠C/=90°
A′
B′
C′
b
a
由勾股定理可知
A′B′ 2=a2+b2
∵a2+b2=c2
∴ A′B′ 2=c2
∴ A′B′=c
在△ABC和△A/B/C/中
BC=a=B/C/
AC=b=A/C/
AB=c=A/B/
∴△ABC≌△A′B′C′(SSS)
A
B
C
b
c
a
【命题】如图, △ABC的三边长为a,b,c,满足 a2+b2=c2
求证:△ABC是直角三角形。
A′
B′
C′
b
a
在△ABC和△A/B/C/中
BC=a=B/C/
AC=b=A/C/
AB=c=A/B/
∴△ABC≌△A′B′C′(SSS)
∴ ∠C=∠C′=90°
∴△ABC是直角三角形。
命题1、如果 直角三角形两直角边分别为a、b,斜边为c,
那么 a2+b2=c2
命题2、如果三角形的三边长a、b、c,满足a2+b2=c2 ,
那么这个三角形是直角三角形。
观察与
命题1和命题2的题设和结论正好相反。
我们把题设和结论正好相反的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
上面我们证明了勾股定理的逆命题是正确的,这个命题也就是一个定理了。我们把这个定理叫做勾股定理的逆定理。
一般地,有的原命题成立,它的逆命题也成立;而还有的原命题成立,它的逆命题不成立;因此,如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理互为逆定理。
练习
说出下列命题的逆命题,这命题正确吗?
⑴ 两条直线平行,内错角相等;
⑵ 如果两个实数相等,那么它们的绝对值相等;
解:⑴ 逆命题是:
内错角相等,两条直线平行;
正确!
⑵ 逆命题是:
如果两个实数的绝对值相等,那么它们相等;
错误!
说出下列命题的逆命题,这命题正确吗?
⑶ 全等三角形的对应角相等;
⑷ 在角的内部,到角的两边距离相等的点
在角的平分线上。
⑶ 逆命题是:
对应角相等的两个三角形全等;
错误!
⑷ 逆命题是:
角平分线上的点到角的两边距离相等。
正确!
例1、判断由线段a,b,c组成的三角形是不是直角三角形:
⑴ a=15,b=8,c=17;
⑵ a=13,b=14,c=15;
解:⑴ ∵ a2+b2=
c2=172=289
∴ a2+b2=c2
这个三角形是直角三角形。
152+82
=225+64=289
例1、判断由线段a,b,c组成的三角形是不是直角三角形:
⑴ a=15,b=8,c=17;
⑵ a=13,b=14,c=15;
解:⑵ ∵ a2+b2=
c2=152=225
∴ a2+b2≠c2
这个三角形不是直角三角形。
132+142
=169+196=365
勾股定理的逆定理与勾股数
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,
那么这个三角形是直角三角形。
满足a2 +b2=c2的三个正整数:
a,b,c称为勾股数。
思考题、如果三条线段a、b、c满足:
a2=c2-b2,这三条线段组成的三角形
是直角三角形吗?为什么?
答:∵ a2=c2-b2
因此,这三条线段组成的三角形
是直角三角形。
∴ a2 +b2 =c2
勾股定理的逆定理的拓展
在 ABC中, a,b,c为三边长,其中 c为最长边。
⑴若a2+b2=c2,则 ABC为直角三角形;
⑵若a2+b2>c2,则 ABC为锐角三角形;
⑶若a2+b2<c2,则 ABC为钝角三角形。
【例2】某港口P位于东西方向海岸线上。“远航”号、“海天”号轮船同时离开港口,各自沿固定方向航行, “远航”号每小时航行16海里, “海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道 “远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
E
N
Q
R
S
解:PQ=16×1.5=24(海里)
PR=12×1.5=18 (海里)
QR=30 (海里)
∵242+182 =302
【例2】某港口P位于东西方向海岸线上。“远航”号、“海天”号轮船同时离开港口,各自沿固定方向航行, “远航”号每小时航行16海里, “海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道 “远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
E
N
Q
R
S
解:PQ=16×1.5=24(海里)
PR=12×1.5=18 (海里)
QR=30 (海里)
∵ PQ2+PR2
海天
远航
=576+324
=900
例2、某港口位于东西方向海岸线上。“远航”号、“海天”号轮船同时离开港口,各自沿固定方向航行, “远航”号每小时航行16海里, “海天”号每小时航行12海里。它们离开港口一个小时后相距30海里。如果知道 “远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
E
N
Q
R
S
∴ PQ2+PR2 =QR2
∴ ∠QPR=90°
∴ ∠RPS=90°-45°=45°
即 “海天”号沿西北方向航行。
∵ PQ2+PR2
=576+324
=900
QR2=900
1、下面三组数是勾股数吗?
⑴ 5,12,13;⑵ 6, 8, 10;⑶ 8,15,17。
解⑴ ∵ 52+122=132
∴ 5,12,13是勾股数。
⑵ ∵ 62+82=102
∴ 6,8,10也是勾股数。
⑶ ∵ 82+152=172
∴ 8,15,17也是勾股数。
2、下列几组数能否作为直角三角形的三边长?
说说你的理由。
⑴9,12,15; ⑵15,36,39;
答:⑴ 92+122=81+144=225=152 能
⑵152+362=225+1296=1521=392 能
⑶122+352=144+1225=1369≠362 不能
⑷122+182=144+324=368≠222 不能
⑶12,35,36; ⑷12,18,22;
3、如果线段a,b,c能组成直角三角形,
则它们的比可能是【 】
A、3∶4∶7; B、5∶12∶13;
C、1∶2∶4; D、1∶3∶5。
B
4、将直角三角形的三边的长度扩大同样的
倍数,则得到的三角形是【 】
A、是直角三角形;
B、可能是锐角三角形;
C、可能是钝角三角形;
D、不可能是直角三角形.
A
5、三角形的三边分别是a,b,c,且满足等式:
(a+b)2-c2=2ab,则此三角形是【 】
A、直角三角形;
B、是锐角三角形;
C、是钝角三角形;
D、是等腰直角三角形.
A
6、已知 ABC中BC=41, AC=40, AB=9,则此三角形为_______三角形,______是最大角。
直角
∠A
7、以 ABC的三条边为边长向外作正方形,依次得到的面积是25,144,169,则这个三角形是 三角形。
直角
8、一个零件的形状如图1,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
C
A
B
D
C
A
B
D
3
4
5
12
13
图1
图2
8、一个零件的形状如图1,按规定这个零件中∠A和∠DBC都应为直角,工人师傅 量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
C
A
B
D
3
4
5
12
13
所以△ABD是直角三角形,∠A是直角。
解:在△ABD中,
∵AB2+AD2
=9+16
=25
BD2=25
∴ AB2+AD2 =BD2
8、一个零件的形状如图1,按规定这个零件中∠A和∠DBC都应为直角,工人师傅 量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
C
A
B
D
3
4
5
12
13
所以△BCD是直角三角形,∠DBC是直角。
在△BCD中,
∵BD2+BC2
=25+144
=169
DC2=169
∴BD2+BC2 =DC2
因此这个零件符合要求。
10、已知 ABC的三边a,b,c满足:
a2+b2+c2+338=10a+24b+26c,
请你判断 ABC的形状,并说明理由。
解:∵ a2+b2+c2+338=10a+24b+26c
∴ a2-10a+b2-24b +c2-26c+338=0
∴ a2-10a+25+b2-24b+144+c2-26c+169=0
∴ (a-5)2+(b-12)2+(c-13)2=0
∴ a=5,b=12,c=13
10、已知 ABC的三边a,b,c满足:
a2+b2+c2+338=10a+24b+26c,
请你判断 ABC的形状,并说明理由。
解:∵ a2+b2+c2+338=10a+24b+26c
∴ a2-10a+b2-24b +c2-26c+338=0
∴ a2-10a+25+b2-24b+144+c2-26c+169=0
∴ (a-5)2+(b-12)2+(c-13)2=0
∴ a=5,b=12,c=13
a2+b2 =c2
ABC是直角三角形。
11、m,n是正整数,则以:
m2-n2, 2mn, m2+n2
为三边长的三角形是直角三角形吗?
解:∵ (m2+n2)2=m4+2m2n2+n4
(m2-n2)2=m4-2m2n2+n4
(2mn)2=4m2n2
∴ (m2-n2)2+(2mn)2=(m2+n2)2
答:是直角三角形。
12、如果将直角三角形的三条边长同时扩大一个相同的倍数,得到的三角形还是直角三角形吗?大写下表,并计算第一列每组数是否为勾股数,它们的2倍、3倍、4倍、10倍呢?
2倍 3倍 4倍 10倍
3,4,5 6,8,10
5,12,13 15,36,39
8,15,17 32,60,68
7,24,25 70,240,250
9,12,15
12,16,20
30,40,50
10,24,26
20,48,52
50,120,130
16,30,34
24,45,51
80,150,170
14,48,50
21,72,75
28,96,100
13、⑴ △ABC中,AB=17cm, BC=30cm, BC上的中线AD=8cm,请你判断△ABC的形状,并说明理由。
A
B
C
17
15
D
8
解:在△ABD中
∵ AD2+BD2
=64+225
=289
AB2 =289
∴ AD2+BD2 = AB2
∴△ABD是直角三角形。
∴∠ADB=90°
∴AD⊥BD
13、⑴ △ABC中,AB=17cm, BC=30cm, BC上的中线AD=8cm,请你判断△ABC的形状,并说明理由。
A
B
C
17
15
D
8
∴△ABD是直角三角形。
∴∠ADB=90°
∴AD⊥BD
∴△ABC是等腰钝角三角形。
13、⑵△ABC的三边分别为a,b,c, 且满足:a2c2-b2c2=a4-b4, 请你判断△ABC的形状,并说明理由。
解:∵ a2c2-b2c2=a4-b4
∴ (a2-b2) c2=(a2+b2) (a2-b2)
∴ a2-b2=0 或 a2+b2=c2
∴△ABC是等腰三角形或直角三角形
或等腰直角三角形.
即 a=b 或 a2+b2=c2
如果三角形的三边长a,b,c满足:
a2 +b2=c2
那么这个三角形是直角三角形。
勾股定理的逆定理
本节重点回顾
满足a2+b2=c2的三个正整数,
称为勾股数。
勾股数
以勾股数为边的三角形是直角三角形。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
17.2 勾股定理的逆定理
人教版 八年级下
勾股定理(gou-gu theorem)
即如果直角三角形两直角边分别为a、b,斜边为c,
那么 a2+b2=c2
直角三角形两直角边的平方和等于斜边的平方。
a
b
c
古代埃及,由于尼罗河的泛滥,给人民的生活带来极大的困难,由于需要多次地对土地进行丈量,却由此产生了数学文明。
据说,古埃及人用如图的方法画直角:
①把一根长绳打上等距离的13个结;
②然后以3个结、4个结、5个结的长度为边长;
③用木桩钉成一个三角形。
5个结的边所对的角便是直角!
0 1 2 3 4 5 6 7 8 9 10 11 12 13
0 1 2 3 4 5 6 7 8 9 10 11 12 13
这就意味着,如果围成的三角形的三边分别为3、4、5,有下面的关系:
32+42 =52
那么围成的三角形是直角三角形。
相传,我国古代大禹治水测量工程时,也用类似的方法确定直角。
画出三边长分别为下面各组数的三角形,度量一下它们是直角三角形吗?
⑴ 2.5cm、6cm、6.5cm;
操作与探究
⑵ 4cm、7.5cm、8.5cm;
⑶ 5cm、6cm、7cm.
画出三边长分别为下面各组数的三角形,度量一下它们是直角三角形吗?
⑴ 2.5cm、6cm、6.5cm;
操作与探究
画出三边长分别为下面各组数的三角形,度量一下它们是直角三角形吗?
⑵ 4cm、7.5cm、8.5cm;
操作与探究
画出三边长分别为下面各组数的三角形,度量一下它们是直角三角形吗?
⑶ 5cm、6cm、7cm.
操作与探究
A
B
C
b
c
a
【命题】如图, △ABC的三边长为a,b,c,满足 a2+b2=c2
求证:△ABC是直角三角形。
证明:画Rt△A/B/C/
使B/C/=a ,A/C/=b,∠C/=90°
A′
B′
C′
b
a
由勾股定理可知
A′B′ 2=a2+b2
∵a2+b2=c2
∴ A′B′ 2=c2
∴ A′B′=c
在△ABC和△A/B/C/中
BC=a=B/C/
AC=b=A/C/
AB=c=A/B/
∴△ABC≌△A′B′C′(SSS)
A
B
C
b
c
a
【命题】如图, △ABC的三边长为a,b,c,满足 a2+b2=c2
求证:△ABC是直角三角形。
A′
B′
C′
b
a
在△ABC和△A/B/C/中
BC=a=B/C/
AC=b=A/C/
AB=c=A/B/
∴△ABC≌△A′B′C′(SSS)
∴ ∠C=∠C′=90°
∴△ABC是直角三角形。
命题1、如果 直角三角形两直角边分别为a、b,斜边为c,
那么 a2+b2=c2
命题2、如果三角形的三边长a、b、c,满足a2+b2=c2 ,
那么这个三角形是直角三角形。
观察与
命题1和命题2的题设和结论正好相反。
我们把题设和结论正好相反的两个命题叫做互逆命题。
如果把其中一个叫做原命题,那么另一个叫做它的逆命题。
上面我们证明了勾股定理的逆命题是正确的,这个命题也就是一个定理了。我们把这个定理叫做勾股定理的逆定理。
一般地,有的原命题成立,它的逆命题也成立;而还有的原命题成立,它的逆命题不成立;因此,如果一个定理的逆命题经过证明是正确的,它也是一个定理,称这两个定理互为逆定理。
练习
说出下列命题的逆命题,这命题正确吗?
⑴ 两条直线平行,内错角相等;
⑵ 如果两个实数相等,那么它们的绝对值相等;
解:⑴ 逆命题是:
内错角相等,两条直线平行;
正确!
⑵ 逆命题是:
如果两个实数的绝对值相等,那么它们相等;
错误!
说出下列命题的逆命题,这命题正确吗?
⑶ 全等三角形的对应角相等;
⑷ 在角的内部,到角的两边距离相等的点
在角的平分线上。
⑶ 逆命题是:
对应角相等的两个三角形全等;
错误!
⑷ 逆命题是:
角平分线上的点到角的两边距离相等。
正确!
例1、判断由线段a,b,c组成的三角形是不是直角三角形:
⑴ a=15,b=8,c=17;
⑵ a=13,b=14,c=15;
解:⑴ ∵ a2+b2=
c2=172=289
∴ a2+b2=c2
这个三角形是直角三角形。
152+82
=225+64=289
例1、判断由线段a,b,c组成的三角形是不是直角三角形:
⑴ a=15,b=8,c=17;
⑵ a=13,b=14,c=15;
解:⑵ ∵ a2+b2=
c2=152=225
∴ a2+b2≠c2
这个三角形不是直角三角形。
132+142
=169+196=365
勾股定理的逆定理与勾股数
如果三角形的三边长a,b,c满足
a2 +b2=c2 ,
那么这个三角形是直角三角形。
满足a2 +b2=c2的三个正整数:
a,b,c称为勾股数。
思考题、如果三条线段a、b、c满足:
a2=c2-b2,这三条线段组成的三角形
是直角三角形吗?为什么?
答:∵ a2=c2-b2
因此,这三条线段组成的三角形
是直角三角形。
∴ a2 +b2 =c2
勾股定理的逆定理的拓展
在 ABC中, a,b,c为三边长,其中 c为最长边。
⑴若a2+b2=c2,则 ABC为直角三角形;
⑵若a2+b2>c2,则 ABC为锐角三角形;
⑶若a2+b2<c2,则 ABC为钝角三角形。
【例2】某港口P位于东西方向海岸线上。“远航”号、“海天”号轮船同时离开港口,各自沿固定方向航行, “远航”号每小时航行16海里, “海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道 “远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
E
N
Q
R
S
解:PQ=16×1.5=24(海里)
PR=12×1.5=18 (海里)
QR=30 (海里)
∵242+182 =302
【例2】某港口P位于东西方向海岸线上。“远航”号、“海天”号轮船同时离开港口,各自沿固定方向航行, “远航”号每小时航行16海里, “海天”号每小时航行12海里。它们离开港口一个半小时后相距30海里。如果知道 “远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
E
N
Q
R
S
解:PQ=16×1.5=24(海里)
PR=12×1.5=18 (海里)
QR=30 (海里)
∵ PQ2+PR2
海天
远航
=576+324
=900
例2、某港口位于东西方向海岸线上。“远航”号、“海天”号轮船同时离开港口,各自沿固定方向航行, “远航”号每小时航行16海里, “海天”号每小时航行12海里。它们离开港口一个小时后相距30海里。如果知道 “远航”号沿东北方向航行,能知道“海天”号沿哪个方向航行吗?
P
E
N
Q
R
S
∴ PQ2+PR2 =QR2
∴ ∠QPR=90°
∴ ∠RPS=90°-45°=45°
即 “海天”号沿西北方向航行。
∵ PQ2+PR2
=576+324
=900
QR2=900
1、下面三组数是勾股数吗?
⑴ 5,12,13;⑵ 6, 8, 10;⑶ 8,15,17。
解⑴ ∵ 52+122=132
∴ 5,12,13是勾股数。
⑵ ∵ 62+82=102
∴ 6,8,10也是勾股数。
⑶ ∵ 82+152=172
∴ 8,15,17也是勾股数。
2、下列几组数能否作为直角三角形的三边长?
说说你的理由。
⑴9,12,15; ⑵15,36,39;
答:⑴ 92+122=81+144=225=152 能
⑵152+362=225+1296=1521=392 能
⑶122+352=144+1225=1369≠362 不能
⑷122+182=144+324=368≠222 不能
⑶12,35,36; ⑷12,18,22;
3、如果线段a,b,c能组成直角三角形,
则它们的比可能是【 】
A、3∶4∶7; B、5∶12∶13;
C、1∶2∶4; D、1∶3∶5。
B
4、将直角三角形的三边的长度扩大同样的
倍数,则得到的三角形是【 】
A、是直角三角形;
B、可能是锐角三角形;
C、可能是钝角三角形;
D、不可能是直角三角形.
A
5、三角形的三边分别是a,b,c,且满足等式:
(a+b)2-c2=2ab,则此三角形是【 】
A、直角三角形;
B、是锐角三角形;
C、是钝角三角形;
D、是等腰直角三角形.
A
6、已知 ABC中BC=41, AC=40, AB=9,则此三角形为_______三角形,______是最大角。
直角
∠A
7、以 ABC的三条边为边长向外作正方形,依次得到的面积是25,144,169,则这个三角形是 三角形。
直角
8、一个零件的形状如图1,按规定这个零件中∠A和∠DBC都应为直角,工人师傅量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
C
A
B
D
C
A
B
D
3
4
5
12
13
图1
图2
8、一个零件的形状如图1,按规定这个零件中∠A和∠DBC都应为直角,工人师傅 量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
C
A
B
D
3
4
5
12
13
所以△ABD是直角三角形,∠A是直角。
解:在△ABD中,
∵AB2+AD2
=9+16
=25
BD2=25
∴ AB2+AD2 =BD2
8、一个零件的形状如图1,按规定这个零件中∠A和∠DBC都应为直角,工人师傅 量得这个零件各边尺寸如图2所示,这个零件符合要求吗?
C
A
B
D
3
4
5
12
13
所以△BCD是直角三角形,∠DBC是直角。
在△BCD中,
∵BD2+BC2
=25+144
=169
DC2=169
∴BD2+BC2 =DC2
因此这个零件符合要求。
10、已知 ABC的三边a,b,c满足:
a2+b2+c2+338=10a+24b+26c,
请你判断 ABC的形状,并说明理由。
解:∵ a2+b2+c2+338=10a+24b+26c
∴ a2-10a+b2-24b +c2-26c+338=0
∴ a2-10a+25+b2-24b+144+c2-26c+169=0
∴ (a-5)2+(b-12)2+(c-13)2=0
∴ a=5,b=12,c=13
10、已知 ABC的三边a,b,c满足:
a2+b2+c2+338=10a+24b+26c,
请你判断 ABC的形状,并说明理由。
解:∵ a2+b2+c2+338=10a+24b+26c
∴ a2-10a+b2-24b +c2-26c+338=0
∴ a2-10a+25+b2-24b+144+c2-26c+169=0
∴ (a-5)2+(b-12)2+(c-13)2=0
∴ a=5,b=12,c=13
a2+b2 =c2
ABC是直角三角形。
11、m,n是正整数,则以:
m2-n2, 2mn, m2+n2
为三边长的三角形是直角三角形吗?
解:∵ (m2+n2)2=m4+2m2n2+n4
(m2-n2)2=m4-2m2n2+n4
(2mn)2=4m2n2
∴ (m2-n2)2+(2mn)2=(m2+n2)2
答:是直角三角形。
12、如果将直角三角形的三条边长同时扩大一个相同的倍数,得到的三角形还是直角三角形吗?大写下表,并计算第一列每组数是否为勾股数,它们的2倍、3倍、4倍、10倍呢?
2倍 3倍 4倍 10倍
3,4,5 6,8,10
5,12,13 15,36,39
8,15,17 32,60,68
7,24,25 70,240,250
9,12,15
12,16,20
30,40,50
10,24,26
20,48,52
50,120,130
16,30,34
24,45,51
80,150,170
14,48,50
21,72,75
28,96,100
13、⑴ △ABC中,AB=17cm, BC=30cm, BC上的中线AD=8cm,请你判断△ABC的形状,并说明理由。
A
B
C
17
15
D
8
解:在△ABD中
∵ AD2+BD2
=64+225
=289
AB2 =289
∴ AD2+BD2 = AB2
∴△ABD是直角三角形。
∴∠ADB=90°
∴AD⊥BD
13、⑴ △ABC中,AB=17cm, BC=30cm, BC上的中线AD=8cm,请你判断△ABC的形状,并说明理由。
A
B
C
17
15
D
8
∴△ABD是直角三角形。
∴∠ADB=90°
∴AD⊥BD
∴△ABC是等腰钝角三角形。
13、⑵△ABC的三边分别为a,b,c, 且满足:a2c2-b2c2=a4-b4, 请你判断△ABC的形状,并说明理由。
解:∵ a2c2-b2c2=a4-b4
∴ (a2-b2) c2=(a2+b2) (a2-b2)
∴ a2-b2=0 或 a2+b2=c2
∴△ABC是等腰三角形或直角三角形
或等腰直角三角形.
即 a=b 或 a2+b2=c2
如果三角形的三边长a,b,c满足:
a2 +b2=c2
那么这个三角形是直角三角形。
勾股定理的逆定理
本节重点回顾
满足a2+b2=c2的三个正整数,
称为勾股数。
勾股数
以勾股数为边的三角形是直角三角形。
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
