26.1.2 反比例函数的图象和性质课件
图片预览






文档简介
(共36张PPT)
26.1.2 反比例函数的图象
和性质
人教版 九年级下
教 学 目 标
1、理解反比例函数的意义。
2、会画出反比例函数的图象,并能说出它的性质。
3、会用待定系数法确定反比例函数的解析式。
我们已经知道了一次函数y=kx+b (k≠0)的图象
是一条直线,二次函数y=ax2+bx+c的图象是抛物线,那么反比例函数 (k为常数,k≠0)的图象是什么样呢?
提出问题
例1、画出反比例函数 的图象。
你还记得如何用 “描点法” 画出函数的图象吗?
描点法画函数图象的方法步骤
列
表
描
点
连
线
注意:①列表时自变量取值要均匀和对称.
②要注意 x≠0.
③尽量选取整数点容易计算和描点.
④连线时要光滑.
描点法画函数图象的方法步骤
列
表
描
点
连
线
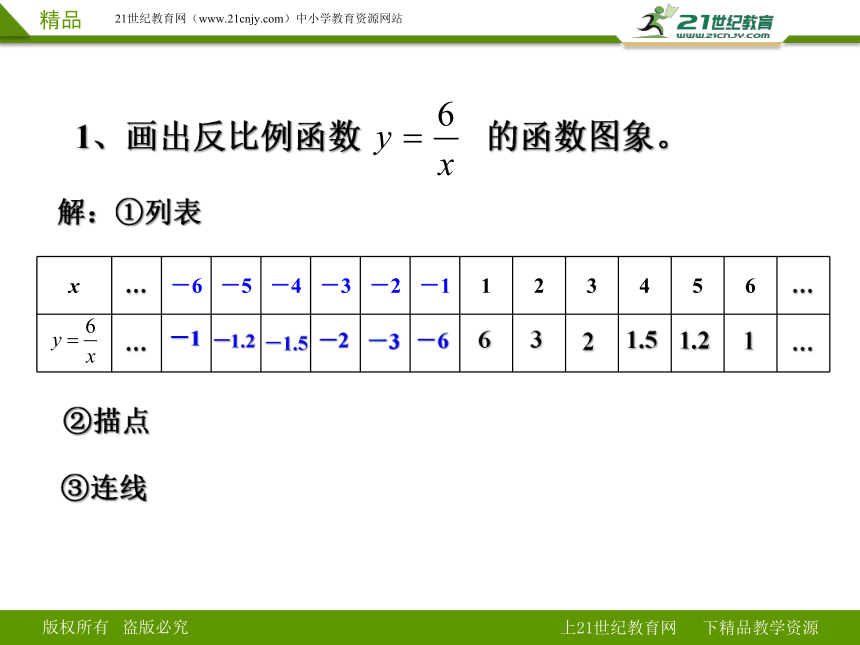
1、画出反比例函数 的函数图象。
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
解:①列表
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… …
②描点
③连线
*
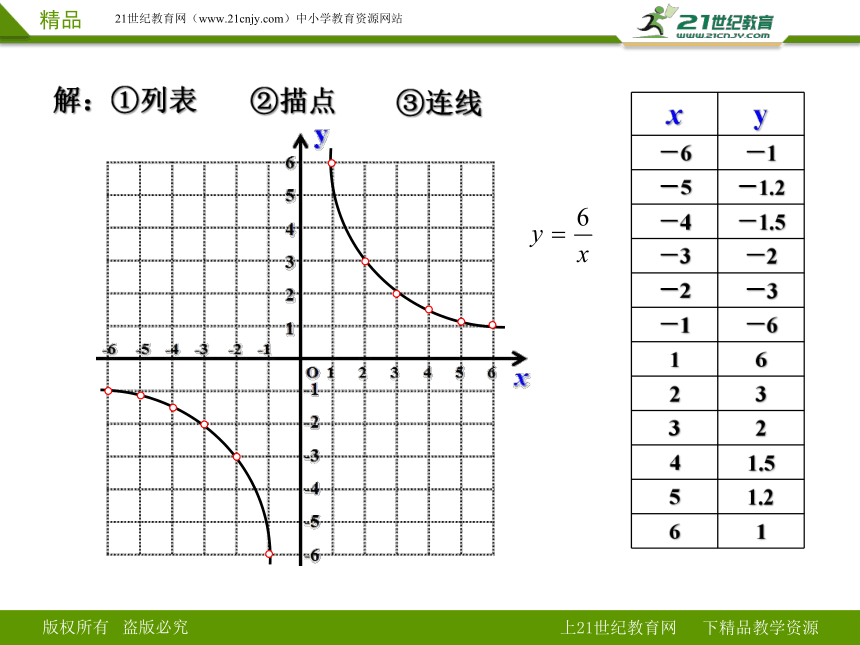
解:①列表
②描点
③连线
x y
-6 -1
-5 -1.2
-4 -1.5
-3 -2
-2 -3
-1 -6
1 6
2 3
3 2
4 1.5
5 1.2
6 1
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… …
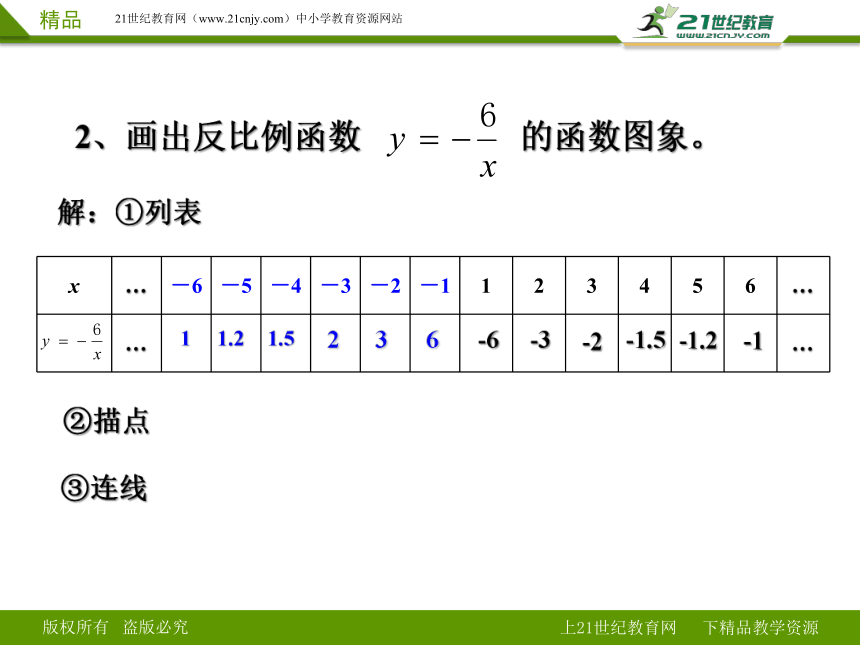
2、画出反比例函数 的函数图象。
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
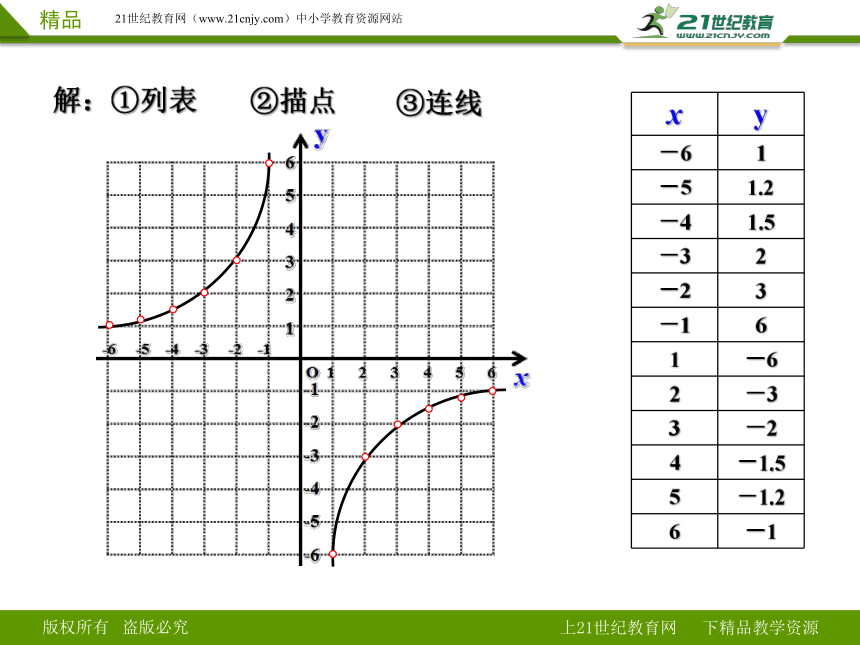
解:①列表
②描点
③连线
*
解:①列表
②描点
③连线
x y
-6 1
-5 1.2
-4 1.5
-3 2
-2 3
-1 6
1 -6
2 -3
3 -2
4 -1.5
5 -1.2
6 -1
4、连线时必须用光滑的曲线连接各点。
5、曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交。
作反比例函数图象时 温馨提醒
1、列表时,自变量的值可以选取一些互为相反数的值,这样既可简化
计算,又便于对称性描点;
2、列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便
连线(平滑的曲线),又较准确地表达函数的变化趋势;
3、描点时一定要养成按自变量从小到大的顺序依次画线,从中体会函数
的增减性;
观察反比例函数
的函数图象可以发现:
⑴它有两条曲线组成;
⑵y随x的增大而减小;
⑶并且y随着│x│的不断增大,曲线越来越接近x轴
⑷y随│x│的减小,曲线越来越接近y轴。
反比例函数的图象叫做双曲线。
k>0
观察反比例函数
的函数图象可以发现:
⑴它也有两条曲线组成;
⑵y随x的增大而增大;
⑶并且y随着│x│的不断增大,曲线越来越接近x轴
⑷y随│x│的减小,曲线越来越接近y轴。
反比例函数的图象叫做双曲线。
k<0
反比例函数图象的性质
1、当k>0时,双曲线的两个分支分别在第一、 三象限内,
在每个象限内,y随x的增大而减小;
2、当k<0时,双曲线的两个分支分别在第二、四象限内,
在每个象限内,y随x的增大而增大。
k>0
k<0
*
P(x,y)
A
B
∵ OA=│x│, OB=│y│
∴ S矩形OAPB=OA·OB
=│x y│
x·y=k
=│k│
S矩形OAPB=│k│
*
P(x,y)
x·y=k
S矩形OAPB=│k│
1、函数 的图象在第 象限,
在每个象限内,y 随 x 的增大而 。
2. 双曲线 经过点(-3, )
巩固练习
二、四
增大
3、函数 的图象在二、四象限,
则m的取值范围是 .
解:m-2<0
m<2
巩固练习
4、对于函数 ,当 x<0时,
⑴ y 随 x 的 而增大;
⑵ 这部分图象在第 ________象限。
减小
三
*
5、三个反比例函数:①y= ;②y= ;③y=
它们在 x 轴上方的图象如图所示,由此推出k1,k2,k3
的大小关系是 。
①
②
③
x
y
O
a
b
c
k1<k2<k3
6、反比例函数
y 随 x 的减小而增大,则m= .
m2+2m-16=-1
3
m2+2m-15=0
(m-3)(m+5)=0
m-3=0 或 m+5=0
m=3 或 m=-5
7、若一次函数y=kx+b的图象经过一、二、四象限,则反比例函数 的图象一定在第 象限。
k<0,b>0
x
y
O
二、四
kb<0
8、设x为一切实数,在下列函数中,当x减小时,
y的值总是增大的函数是【 】
(A) y =-5x-1 (B)
(C) y=-2x+2; (D) y=4x
C
(C)
9、指出下列图象中, 【 】是y=kx与 (k≠0) 在同一平面直角坐标系中的图象。
D
(A)
(B)
(D)
10、已知k<0,则函数 y1=kx,y2= 在同一
坐标系中的图象大致是 【 】
D
(A)
(B)
(C)
(D)
11、已知k>0,则函数 y1=kx+k,y2= 在同一坐标系中的图象大致是 【 】
C
(A)
(B)
(C)
(D)
*
12、已知常数k<0,b>0,则函数 y=kx+b,
y= 的图象可能是 【 】
(A)
(B)
(C)
(D)
D
*
13、反比例函数 y= 的图象如图所示,
以下结论正确的是 【 】
C
①常数m<-1; ②在每个象限内,y随x的增大而增大;
③若A(-1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(-x,-y)也在图象上.
(A)①②; (B) ②③; (C)③④; (D)①④.
*
14、正比例函数 y=kx和反比例函数 y=
(k≠0的常数)在同一坐标系中的图象可能是【 】
(A)
(B)
(C)
(D)
C
*
15、阅读材料:反比例函数y= (k≠0)的本质特征是两个变量x与y的积是一个常数k,即 xy=k (k≠0)。由此,不难得出系数k的几何意义:如图①,过双曲线y= (k≠0)上任意一点P(x,y)作PM⊥x轴于M、PN⊥y轴于N,则有PM=│y│,PN=│x│,所以S矩形PMON=│xy│=│k│,S△POM=S△PON
= │k│,
利用材料中的信息,可以解决许多
与图形面积有关的问题:
图①
*
如图②,点A在双曲线y= 上,AB⊥x轴于点B,
且△AOB的面积为2,求 k 的值。
图②
解:∵ S△AOB= │k│
= 2
∴ │k│=4
∵ 图象在二、四象限内,
∴ k<0
∴ k=-4
*
16、如图,菱形ABCO的顶点C的坐标为(3,4),顶点A在 x轴 的正半轴上,反比例函数 y= (x>0) 的图象经过顶点B,则k的值为 .
O
A
B
C
x
y
D
E
在Rt△OCD中,
OD=3,CD=4
∴ OC=5
∴ DE=CB=OC=5
∴ B(8,4)
∴ OE=OD+DE=8
32
*
17、如果点A(-2,y1),B(-1,y2),C(2,y3)都在反比例函数 y= (k>0) 的图象上,那么y1,y2,y3的大小关系是【 】
y1<y3<y2; (B) y2<y1<y3;
(C) y1<y2<y3; (D) y3<y2<y1.
y1
y2
y3
-2
-1
2
B
*
18、已知直线 y=2x+1与双曲线 y=
交于点P(1,n).
⑴ 求m的值;
解:⑴ 将点P(1,n)代入直线y=2x+1,得
n=3
∴点P(1,3)
再将点P(1,3)代入双曲线,得
m=2
⑵ 若点A(x1,y1),B(x2,y2)在双曲线 y= 上,
且x1<x2<0,试比较y1,y2的大小。
*
⑵由⑴知双曲线解析式为:
在每个象限内y随x的增大而减小。
∴ 当x1<x2<0时,
∴ y1>y2
y1
y2
x1
x2
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
26.1.2 反比例函数的图象
和性质
人教版 九年级下
教 学 目 标
1、理解反比例函数的意义。
2、会画出反比例函数的图象,并能说出它的性质。
3、会用待定系数法确定反比例函数的解析式。
我们已经知道了一次函数y=kx+b (k≠0)的图象
是一条直线,二次函数y=ax2+bx+c的图象是抛物线,那么反比例函数 (k为常数,k≠0)的图象是什么样呢?
提出问题
例1、画出反比例函数 的图象。
你还记得如何用 “描点法” 画出函数的图象吗?
描点法画函数图象的方法步骤
列
表
描
点
连
线
注意:①列表时自变量取值要均匀和对称.
②要注意 x≠0.
③尽量选取整数点容易计算和描点.
④连线时要光滑.
描点法画函数图象的方法步骤
列
表
描
点
连
线
1、画出反比例函数 的函数图象。
-1
-1.2
-1.5
-2
-3
-6
6
3
2
1.5
1.2
1
解:①列表
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… …
②描点
③连线
*
解:①列表
②描点
③连线
x y
-6 -1
-5 -1.2
-4 -1.5
-3 -2
-2 -3
-1 -6
1 6
2 3
3 2
4 1.5
5 1.2
6 1
x … -6 -5 -4 -3 -2 -1 1 2 3 4 5 6 …
… …
2、画出反比例函数 的函数图象。
1
1.2
1.5
2
3
6
-6
-3
-2
-1.5
-1.2
-1
解:①列表
②描点
③连线
*
解:①列表
②描点
③连线
x y
-6 1
-5 1.2
-4 1.5
-3 2
-2 3
-1 6
1 -6
2 -3
3 -2
4 -1.5
5 -1.2
6 -1
4、连线时必须用光滑的曲线连接各点。
5、曲线的发展趋势只能靠近坐标轴,但不能和坐标轴相交。
作反比例函数图象时 温馨提醒
1、列表时,自变量的值可以选取一些互为相反数的值,这样既可简化
计算,又便于对称性描点;
2、列表描点时,要尽量多取一些数值,多描一些点,这样既可以方便
连线(平滑的曲线),又较准确地表达函数的变化趋势;
3、描点时一定要养成按自变量从小到大的顺序依次画线,从中体会函数
的增减性;
观察反比例函数
的函数图象可以发现:
⑴它有两条曲线组成;
⑵y随x的增大而减小;
⑶并且y随着│x│的不断增大,曲线越来越接近x轴
⑷y随│x│的减小,曲线越来越接近y轴。
反比例函数的图象叫做双曲线。
k>0
观察反比例函数
的函数图象可以发现:
⑴它也有两条曲线组成;
⑵y随x的增大而增大;
⑶并且y随着│x│的不断增大,曲线越来越接近x轴
⑷y随│x│的减小,曲线越来越接近y轴。
反比例函数的图象叫做双曲线。
k<0
反比例函数图象的性质
1、当k>0时,双曲线的两个分支分别在第一、 三象限内,
在每个象限内,y随x的增大而减小;
2、当k<0时,双曲线的两个分支分别在第二、四象限内,
在每个象限内,y随x的增大而增大。
k>0
k<0
*
P(x,y)
A
B
∵ OA=│x│, OB=│y│
∴ S矩形OAPB=OA·OB
=│x y│
x·y=k
=│k│
S矩形OAPB=│k│
*
P(x,y)
x·y=k
S矩形OAPB=│k│
1、函数 的图象在第 象限,
在每个象限内,y 随 x 的增大而 。
2. 双曲线 经过点(-3, )
巩固练习
二、四
增大
3、函数 的图象在二、四象限,
则m的取值范围是 .
解:m-2<0
m<2
巩固练习
4、对于函数 ,当 x<0时,
⑴ y 随 x 的 而增大;
⑵ 这部分图象在第 ________象限。
减小
三
*
5、三个反比例函数:①y= ;②y= ;③y=
它们在 x 轴上方的图象如图所示,由此推出k1,k2,k3
的大小关系是 。
①
②
③
x
y
O
a
b
c
k1<k2<k3
6、反比例函数
y 随 x 的减小而增大,则m= .
m2+2m-16=-1
3
m2+2m-15=0
(m-3)(m+5)=0
m-3=0 或 m+5=0
m=3 或 m=-5
7、若一次函数y=kx+b的图象经过一、二、四象限,则反比例函数 的图象一定在第 象限。
k<0,b>0
x
y
O
二、四
kb<0
8、设x为一切实数,在下列函数中,当x减小时,
y的值总是增大的函数是【 】
(A) y =-5x-1 (B)
(C) y=-2x+2; (D) y=4x
C
(C)
9、指出下列图象中, 【 】是y=kx与 (k≠0) 在同一平面直角坐标系中的图象。
D
(A)
(B)
(D)
10、已知k<0,则函数 y1=kx,y2= 在同一
坐标系中的图象大致是 【 】
D
(A)
(B)
(C)
(D)
11、已知k>0,则函数 y1=kx+k,y2= 在同一坐标系中的图象大致是 【 】
C
(A)
(B)
(C)
(D)
*
12、已知常数k<0,b>0,则函数 y=kx+b,
y= 的图象可能是 【 】
(A)
(B)
(C)
(D)
D
*
13、反比例函数 y= 的图象如图所示,
以下结论正确的是 【 】
C
①常数m<-1; ②在每个象限内,y随x的增大而增大;
③若A(-1,h),B(2,k)在图象上,则h<k;
④若P(x,y)在图象上,则P′(-x,-y)也在图象上.
(A)①②; (B) ②③; (C)③④; (D)①④.
*
14、正比例函数 y=kx和反比例函数 y=
(k≠0的常数)在同一坐标系中的图象可能是【 】
(A)
(B)
(C)
(D)
C
*
15、阅读材料:反比例函数y= (k≠0)的本质特征是两个变量x与y的积是一个常数k,即 xy=k (k≠0)。由此,不难得出系数k的几何意义:如图①,过双曲线y= (k≠0)上任意一点P(x,y)作PM⊥x轴于M、PN⊥y轴于N,则有PM=│y│,PN=│x│,所以S矩形PMON=│xy│=│k│,S△POM=S△PON
= │k│,
利用材料中的信息,可以解决许多
与图形面积有关的问题:
图①
*
如图②,点A在双曲线y= 上,AB⊥x轴于点B,
且△AOB的面积为2,求 k 的值。
图②
解:∵ S△AOB= │k│
= 2
∴ │k│=4
∵ 图象在二、四象限内,
∴ k<0
∴ k=-4
*
16、如图,菱形ABCO的顶点C的坐标为(3,4),顶点A在 x轴 的正半轴上,反比例函数 y= (x>0) 的图象经过顶点B,则k的值为 .
O
A
B
C
x
y
D
E
在Rt△OCD中,
OD=3,CD=4
∴ OC=5
∴ DE=CB=OC=5
∴ B(8,4)
∴ OE=OD+DE=8
32
*
17、如果点A(-2,y1),B(-1,y2),C(2,y3)都在反比例函数 y= (k>0) 的图象上,那么y1,y2,y3的大小关系是【 】
y1<y3<y2; (B) y2<y1<y3;
(C) y1<y2<y3; (D) y3<y2<y1.
y1
y2
y3
-2
-1
2
B
*
18、已知直线 y=2x+1与双曲线 y=
交于点P(1,n).
⑴ 求m的值;
解:⑴ 将点P(1,n)代入直线y=2x+1,得
n=3
∴点P(1,3)
再将点P(1,3)代入双曲线,得
m=2
⑵ 若点A(x1,y1),B(x2,y2)在双曲线 y= 上,
且x1<x2<0,试比较y1,y2的大小。
*
⑵由⑴知双曲线解析式为:
在每个象限内y随x的增大而减小。
∴ 当x1<x2<0时,
∴ y1>y2
y1
y2
x1
x2
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
