26.2.2 实际问题与反比例函数课件
图片预览










文档简介
(共40张PPT)
26.2.2 实际问题与反比例函数
人教版 九年级下
教 学 目 标
1、理解反比例函数的意义;
2、会用待定系数法确定反比例函数的解析式;
3、会应用反比例函数解决实际问题。
1、如果等腰三角形的底边长为x,底边上的高为y,
面积为s(一定),则y关于x的函数解析式为【 】
(A) (B)
(C) (D)
C
课堂练习
一、选择题 (共3道题)
高=2×面积÷底
*
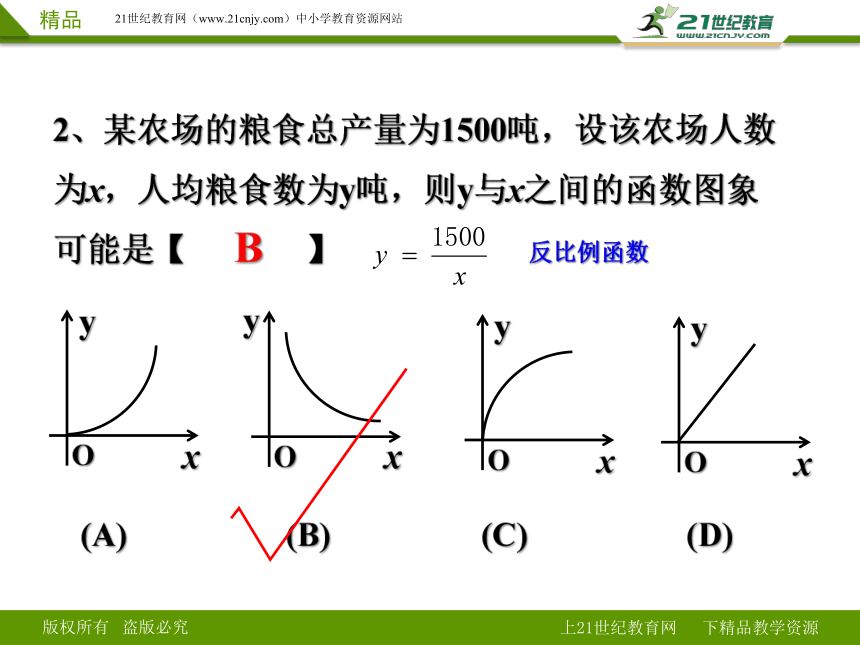
2、某农场的粮食总产量为1500吨,设该农场人数为x,人均粮食数为y吨,则y与x之间的函数图象可能是【 】
B
x
y
O
x
y
O
x
y
O
x
y
O
(A) (B) (C) (D)
反比例函数
*
3、甲、乙两地相距skm,汽车从甲地以vkm/h的速度开往乙地,所需时间是th,则下列说法正确的是【 】
A.当t为定值时,s与v成反比例;
B.当v为定值时,s与t成反比例;
C.当s为定值时,t与v成反比例;
D.以上均不正确。
s=t·v
s=v·t
C
一、选择题 (共3道题)
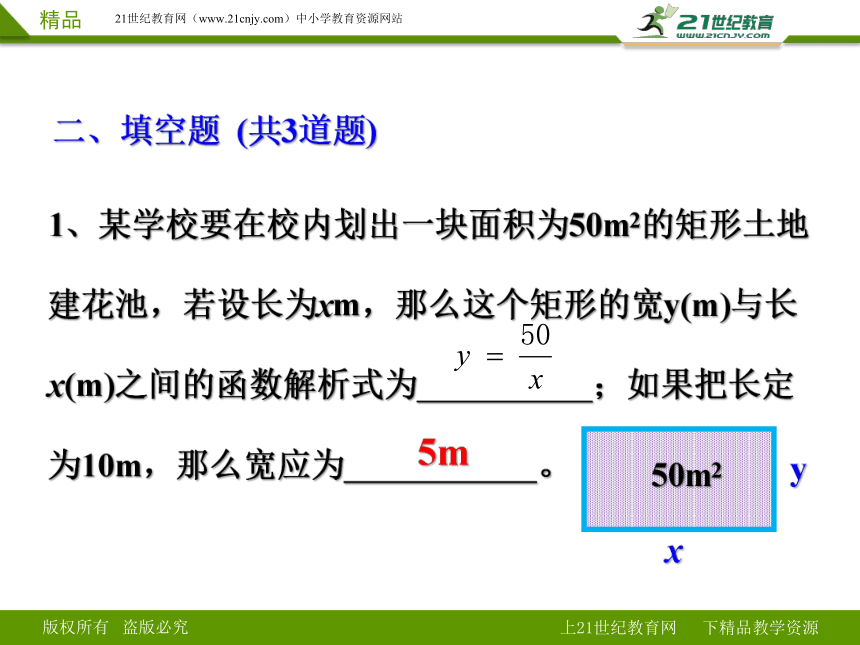
1、某学校要在校内划出一块面积为50m2的矩形土地建花池,若设长为xm,那么这个矩形的宽y(m)与长x(m)之间的函数解析式为 ;如果把长定为10m,那么宽应为 。
5m
二、填空题 (共3道题)
50m2
y
x
2、某水果生产基地准备将180吨的某种水果运往某地销售,若每天运送水果x吨,需要y天完成任务,则y与x的函数解析式是 ;如果计划2天完成任务,那么每天应运送水果 吨。
二、填空题 (共3道题)
时间=工作量÷工作效率
90
3、★人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体时是动态的,车速增加,视野变窄,当车速为50km/h时,视角为80°,如果视角f(度)是车速v(km/h)的反比例函数,那么f,v之之间的函数解析式为 ;当车速为100km/h时,视野的度数是 。
fv=80×50
二、填空题 (共3道题)
40°
1、某农科所研制了一种小麦新品种,2017年决定
选取4500kg在某地区试种。
⑴ 写出可试种的亩数 y (亩) 与每亩所需的新品种的
质量 x (kg)之间的函数解析式;
三、解答题 (共10道题)
总面积×单位面积的质量数=总质量
解: ⑴ y与 x之间的函数解析式为:
⑵ 若每亩需新品种15kg,则这些新品种可试种多少
亩土地?
解:⑴ y与 x之间的函数解析式为:
⑵ 当x=15时,
=300 (亩)
2、某蓄水池的排水管每小时排水8m3,6小时可将
满池水全部排空。
⑴ 该蓄水池的容积是多少?
解: ⑴ 蓄水池的容积是:
8×6= 48 (m3)
答: 蓄水池的容积是48m3.
⑵ 若增加排水管,使每小时的排水量达到 Q(m3),
那么将一满池水排空所需的时间t(小时)与 Q(m3)
之间有怎样的函数关系?
根据:每小时的排水量×时间=水池容积
⑵ Q与 t 之间的函数解析式为:
⑶ 如果准备在5小时内将一满池水排空,那么每小时
的排水量至少应为多少立方米?
⑵ Q与 t 之间的函数解析式为:
⑶ 当t=5时,
=9.6 (立方米)
⑷ 已知排水管每小时最多排水12m3,那么至少需要
多少小时可将一满池水全部排空?
⑵ Q与 t 之间的函数解析式为:
⑶ 当t=5时,
=9.6 (立方米)
⑷ 当Q=12时,
t=4
3、李琳家的客厅地面需要重新装修,面积为30m2.
⑴ 所需地板砖的块数n与每块地板砖的面积S有怎样
的函数关系?
⑵ 若选购的是边长为50cm的正方形地板砖,
则至少需要地板砖多少块?
解:⑴ n与 S 之间的函数解析式为:
3、李琳家的客厅地面需要重新装修,面积为30m2.
⑵ 若选购的是边长为50cm的正方形地板砖,
则至少需要地板砖多少块?
解:⑴ n与 S 之间的函数解析式为:
⑵ 当 S =0.52=0.25时
=120 (块)
4、一个长方体水池的容积是240m3,它的长是ym,
宽是6m,深是xm.
⑴ 写出用x表示y的函数解析式;
根据:长×宽×深=水池的容积
即:y×6×x=240
解:⑴用x表示y的函数解析式为:
4、一个长方体水池的容积是240m3,它的长是ym,
宽是6m,深是xm.
⑵ 若池边的警示牌上写着“水深2.5m,严禁游泳,
危险”,请计算一下水池的长。
⑵ 当 x =2.5时
=16(m)
答:水池的长为16米。
5、某工程队接了一项开挖水渠的工程,如果每天完成的工程量为24m,50天就能完成任务。设完成任务用时y天,每天完成的工程量为xm.
⑴ 共需开挖水渠多长?
24×50=
解:⑴共需开挖水渠的长为:
1200 (米)
5、某工程队接了一项开挖水渠的工程,如果每天完成的工程量为24m,50天就能完成任务。设完成任务用时y天,每天完成的工程量为xm.
⑵ 写出y与x之间的函数解析式;
⑵ y与x之间的函数解析式为:
⑶ 如果为了防汛工作的紧急需要,必须在35天内完成任务,那么每天至少需要完成的工程量是多少?(保留整数)。
⑶ 当 y=35 时
x≈35(m) 注:必须用进1法
答:每天至少需要完成的工程量约是35米。
6、小江驾车从A地到B地,每小时行驶75km,刚好用了4小时,某天上午9点小刘驾车从B地去A地,驾车的平均速度为y(km/h),行驶时间为x(h).
⑴ A、B两地相距多远?
75×4=
解:⑴ A、B两地相距:
300 (km)
答: A、B两地相距300km.
6、小江驾车从A地到B地,每小时行驶75km,刚好用了4小时,某天上午9点小刘驾车从B地去A地,驾车的平均速度为y(km/h),行驶时间为x(h).
⑵ 写出小刘驾车的平均速度y(km/h)与行驶时间x(h)
之间的函数解析式;
⑵ y与x之间的函数解析式为:
6、小江驾车从A地到B地,每小时行驶75km,刚好用了4小时,某天上午9点小刘驾车从B地去A地,驾车的平均速度为y(km/h),行驶时间为x(h).
⑶ 若小刘要在下午14点恰好到达A地,其驾车平均
速度应满足什么条件?
⑶ 当 x=5 时
=60
答:小刘驾车的平均速度应为60km/h。
⑷ 为了保证安全,车速不得超过80km/h,那么小刘
最早几点到达A地?
⑷ 当 y=80 时
x=3.75
答:小刘最早12时45分到达A地。
9时+3时45分=12时45分
7、甲、乙两家商场进行促销活动,甲商场采用“满200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元······乙商场按顾客购买商品的总金额打6折促销.
⑴ 若顾客在甲商场购买了510元的商品,付款时应付
多少钱?
解:⑴ 应付:
510-200=
310 (元)
⑵ 顾客在甲商场购买商品的总金额为x(400≤x<600)
元,优惠后得到商家的优惠率为P(P=优惠金额
÷购买商品的总金额),写出P与x之间的函数
关系式,并说明P随x的变化情况。
⑵ 写出P与x之间的函数关系式为:
在400≤x<600范围内P随x的增大而减小。
⑶ 品牌、质量、规格等都相同的某商品,在甲、乙两商场的标价都是 x(200≤x<400)元,你认为选择哪家商场购买该商品花钱较少?说明理由。
⑶在甲商场应付款:
(x-100)元
在乙商场应付款:
0.6x元
①如果付款相同时,则
x-100=0.6x
x=250
②如果甲付款少,则
x-100<0.6x
x<250
③如果乙付款少,则
x-100>0.6x
x>250
8、一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系式 ,其图象为如图所示的一段曲线,且点为A(40,1)和B(m,0.5)。
⑴ 求k和m的值。
A
B
1
0.5
40 m v
t
O
解:⑴ 将A(40,1)代入,得
k=40×1
=40
t与v的函数关系式为:
再将B(m,0.5)代入,得
=80
8、一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系式 ,其图象为如图所示的一段曲线,且点为A(40,1)和B(m,0.5)。
A
B
1
0.5
40 m v
t
O
⑵ 若行驶速度不得超过60km/h,则
汽车通过该路段最少需要多长时间?
⑵当v=60时,
答:汽车通过该路段最小需要 小时。
9、实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(h)的关系可近似地用二次函数y=-200x2+100x刻画,1.5小时后(包括1.5小时)y与x可近似地用反比例函数 (k>0)刻画(如图)
⑴根据上述数学模型计算:
①喝酒几小时后血液中的酒精含量达到最大值?最大值为多少?
① 喝酒几小时后血液中的酒精含量达到最大值?
最大值为多少?
y=-200x2+100x
(0≤x<1.5)
解:⑴ ① 当0≤x<1.5时,
=0.25
=12.5
②当x=5时,y=45,求k的值;
②将x=5,y=45代入,得
k=5×45
=225
⑵按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路,参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,则他第二天早上7:00能否驾车去上班?请说明理由。
⑶由②知,
当x=11时,
当x≥1.5时,
≈20.45
答:他不能驾车上班。
10、据媒报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”。已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题: ⑴写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
解:⑴设双曲线为:
则k=25×6
=150
∴双曲线解析式为:
⑴写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
解:⑴设双曲线为:
则k=25×6
=150
∴双曲线解析式为:
当y=10时,
y=mx
设线段OA的解析式为:
=15
∴A(15,10)
将点A(15,10)代入上式,得
⑴写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
将点A(15,10)代入上式,得
∴线段OA的解析式为:
∴y与x的函数关系式为:
y=
(0≤x<15)
(x>15)
⑵据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
∴y与x的函数关系式为:
y=
(0≤x<15)
(x>15)
⑵当y=2时,
=75
答:至少75分钟时间内,师生不能进入教室.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
26.2.2 实际问题与反比例函数
人教版 九年级下
教 学 目 标
1、理解反比例函数的意义;
2、会用待定系数法确定反比例函数的解析式;
3、会应用反比例函数解决实际问题。
1、如果等腰三角形的底边长为x,底边上的高为y,
面积为s(一定),则y关于x的函数解析式为【 】
(A) (B)
(C) (D)
C
课堂练习
一、选择题 (共3道题)
高=2×面积÷底
*
2、某农场的粮食总产量为1500吨,设该农场人数为x,人均粮食数为y吨,则y与x之间的函数图象可能是【 】
B
x
y
O
x
y
O
x
y
O
x
y
O
(A) (B) (C) (D)
反比例函数
*
3、甲、乙两地相距skm,汽车从甲地以vkm/h的速度开往乙地,所需时间是th,则下列说法正确的是【 】
A.当t为定值时,s与v成反比例;
B.当v为定值时,s与t成反比例;
C.当s为定值时,t与v成反比例;
D.以上均不正确。
s=t·v
s=v·t
C
一、选择题 (共3道题)
1、某学校要在校内划出一块面积为50m2的矩形土地建花池,若设长为xm,那么这个矩形的宽y(m)与长x(m)之间的函数解析式为 ;如果把长定为10m,那么宽应为 。
5m
二、填空题 (共3道题)
50m2
y
x
2、某水果生产基地准备将180吨的某种水果运往某地销售,若每天运送水果x吨,需要y天完成任务,则y与x的函数解析式是 ;如果计划2天完成任务,那么每天应运送水果 吨。
二、填空题 (共3道题)
时间=工作量÷工作效率
90
3、★人的视觉机能受运动速度的影响很大,行驶中司机在驾驶室内观察前方物体时是动态的,车速增加,视野变窄,当车速为50km/h时,视角为80°,如果视角f(度)是车速v(km/h)的反比例函数,那么f,v之之间的函数解析式为 ;当车速为100km/h时,视野的度数是 。
fv=80×50
二、填空题 (共3道题)
40°
1、某农科所研制了一种小麦新品种,2017年决定
选取4500kg在某地区试种。
⑴ 写出可试种的亩数 y (亩) 与每亩所需的新品种的
质量 x (kg)之间的函数解析式;
三、解答题 (共10道题)
总面积×单位面积的质量数=总质量
解: ⑴ y与 x之间的函数解析式为:
⑵ 若每亩需新品种15kg,则这些新品种可试种多少
亩土地?
解:⑴ y与 x之间的函数解析式为:
⑵ 当x=15时,
=300 (亩)
2、某蓄水池的排水管每小时排水8m3,6小时可将
满池水全部排空。
⑴ 该蓄水池的容积是多少?
解: ⑴ 蓄水池的容积是:
8×6= 48 (m3)
答: 蓄水池的容积是48m3.
⑵ 若增加排水管,使每小时的排水量达到 Q(m3),
那么将一满池水排空所需的时间t(小时)与 Q(m3)
之间有怎样的函数关系?
根据:每小时的排水量×时间=水池容积
⑵ Q与 t 之间的函数解析式为:
⑶ 如果准备在5小时内将一满池水排空,那么每小时
的排水量至少应为多少立方米?
⑵ Q与 t 之间的函数解析式为:
⑶ 当t=5时,
=9.6 (立方米)
⑷ 已知排水管每小时最多排水12m3,那么至少需要
多少小时可将一满池水全部排空?
⑵ Q与 t 之间的函数解析式为:
⑶ 当t=5时,
=9.6 (立方米)
⑷ 当Q=12时,
t=4
3、李琳家的客厅地面需要重新装修,面积为30m2.
⑴ 所需地板砖的块数n与每块地板砖的面积S有怎样
的函数关系?
⑵ 若选购的是边长为50cm的正方形地板砖,
则至少需要地板砖多少块?
解:⑴ n与 S 之间的函数解析式为:
3、李琳家的客厅地面需要重新装修,面积为30m2.
⑵ 若选购的是边长为50cm的正方形地板砖,
则至少需要地板砖多少块?
解:⑴ n与 S 之间的函数解析式为:
⑵ 当 S =0.52=0.25时
=120 (块)
4、一个长方体水池的容积是240m3,它的长是ym,
宽是6m,深是xm.
⑴ 写出用x表示y的函数解析式;
根据:长×宽×深=水池的容积
即:y×6×x=240
解:⑴用x表示y的函数解析式为:
4、一个长方体水池的容积是240m3,它的长是ym,
宽是6m,深是xm.
⑵ 若池边的警示牌上写着“水深2.5m,严禁游泳,
危险”,请计算一下水池的长。
⑵ 当 x =2.5时
=16(m)
答:水池的长为16米。
5、某工程队接了一项开挖水渠的工程,如果每天完成的工程量为24m,50天就能完成任务。设完成任务用时y天,每天完成的工程量为xm.
⑴ 共需开挖水渠多长?
24×50=
解:⑴共需开挖水渠的长为:
1200 (米)
5、某工程队接了一项开挖水渠的工程,如果每天完成的工程量为24m,50天就能完成任务。设完成任务用时y天,每天完成的工程量为xm.
⑵ 写出y与x之间的函数解析式;
⑵ y与x之间的函数解析式为:
⑶ 如果为了防汛工作的紧急需要,必须在35天内完成任务,那么每天至少需要完成的工程量是多少?(保留整数)。
⑶ 当 y=35 时
x≈35(m) 注:必须用进1法
答:每天至少需要完成的工程量约是35米。
6、小江驾车从A地到B地,每小时行驶75km,刚好用了4小时,某天上午9点小刘驾车从B地去A地,驾车的平均速度为y(km/h),行驶时间为x(h).
⑴ A、B两地相距多远?
75×4=
解:⑴ A、B两地相距:
300 (km)
答: A、B两地相距300km.
6、小江驾车从A地到B地,每小时行驶75km,刚好用了4小时,某天上午9点小刘驾车从B地去A地,驾车的平均速度为y(km/h),行驶时间为x(h).
⑵ 写出小刘驾车的平均速度y(km/h)与行驶时间x(h)
之间的函数解析式;
⑵ y与x之间的函数解析式为:
6、小江驾车从A地到B地,每小时行驶75km,刚好用了4小时,某天上午9点小刘驾车从B地去A地,驾车的平均速度为y(km/h),行驶时间为x(h).
⑶ 若小刘要在下午14点恰好到达A地,其驾车平均
速度应满足什么条件?
⑶ 当 x=5 时
=60
答:小刘驾车的平均速度应为60km/h。
⑷ 为了保证安全,车速不得超过80km/h,那么小刘
最早几点到达A地?
⑷ 当 y=80 时
x=3.75
答:小刘最早12时45分到达A地。
9时+3时45分=12时45分
7、甲、乙两家商场进行促销活动,甲商场采用“满200减100”的促销方式,即购买商品的总金额满200元但不足400元,少付100元;满400元但不足600元,少付200元······乙商场按顾客购买商品的总金额打6折促销.
⑴ 若顾客在甲商场购买了510元的商品,付款时应付
多少钱?
解:⑴ 应付:
510-200=
310 (元)
⑵ 顾客在甲商场购买商品的总金额为x(400≤x<600)
元,优惠后得到商家的优惠率为P(P=优惠金额
÷购买商品的总金额),写出P与x之间的函数
关系式,并说明P随x的变化情况。
⑵ 写出P与x之间的函数关系式为:
在400≤x<600范围内P随x的增大而减小。
⑶ 品牌、质量、规格等都相同的某商品,在甲、乙两商场的标价都是 x(200≤x<400)元,你认为选择哪家商场购买该商品花钱较少?说明理由。
⑶在甲商场应付款:
(x-100)元
在乙商场应付款:
0.6x元
①如果付款相同时,则
x-100=0.6x
x=250
②如果甲付款少,则
x-100<0.6x
x<250
③如果乙付款少,则
x-100>0.6x
x>250
8、一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系式 ,其图象为如图所示的一段曲线,且点为A(40,1)和B(m,0.5)。
⑴ 求k和m的值。
A
B
1
0.5
40 m v
t
O
解:⑴ 将A(40,1)代入,得
k=40×1
=40
t与v的函数关系式为:
再将B(m,0.5)代入,得
=80
8、一辆汽车匀速通过某段公路,所需时间t(h)与行驶速度v(km/h)满足函数关系式 ,其图象为如图所示的一段曲线,且点为A(40,1)和B(m,0.5)。
A
B
1
0.5
40 m v
t
O
⑵ 若行驶速度不得超过60km/h,则
汽车通过该路段最少需要多长时间?
⑵当v=60时,
答:汽车通过该路段最小需要 小时。
9、实验数据显示,一般成人喝半斤低度白酒后,1.5小时内其血液中酒精含量y(毫克/百毫升)与时间x(h)的关系可近似地用二次函数y=-200x2+100x刻画,1.5小时后(包括1.5小时)y与x可近似地用反比例函数 (k>0)刻画(如图)
⑴根据上述数学模型计算:
①喝酒几小时后血液中的酒精含量达到最大值?最大值为多少?
① 喝酒几小时后血液中的酒精含量达到最大值?
最大值为多少?
y=-200x2+100x
(0≤x<1.5)
解:⑴ ① 当0≤x<1.5时,
=0.25
=12.5
②当x=5时,y=45,求k的值;
②将x=5,y=45代入,得
k=5×45
=225
⑵按国家规定,车辆驾驶人员血液中的酒精含量大于或等于20毫克/百毫升时属于“酒后驾驶”,不能驾车上路,参照上述数学模型,假设某驾驶员晚上20:00在家喝完半斤低度白酒,则他第二天早上7:00能否驾车去上班?请说明理由。
⑶由②知,
当x=11时,
当x≥1.5时,
≈20.45
答:他不能驾车上班。
10、据媒报道,近期“手足口病”可能进入发病高峰期,某校根据《学校卫生工作条例》,为预防“手足口病”,对教室进行“薰药消毒”。已知药物在燃烧机释放过程中,室内空气中每立方米含药量y(毫克)与燃烧时间x(分钟)之间的关系如图所示(即图中线段OA和双曲线在A点及其右侧的部分),根据图象所示信息,解答下列问题: ⑴写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
解:⑴设双曲线为:
则k=25×6
=150
∴双曲线解析式为:
⑴写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
解:⑴设双曲线为:
则k=25×6
=150
∴双曲线解析式为:
当y=10时,
y=mx
设线段OA的解析式为:
=15
∴A(15,10)
将点A(15,10)代入上式,得
⑴写出从药物释放开始,y与x之间的函数关系式及自变量的取值范围;
将点A(15,10)代入上式,得
∴线段OA的解析式为:
∴y与x的函数关系式为:
y=
(0≤x<15)
(x>15)
⑵据测定,当空气中每立方米的含药量低于2毫克时,对人体无毒害作用,那么从消毒开始,至少在多长时间内,师生不能进入教室?
∴y与x的函数关系式为:
y=
(0≤x<15)
(x>15)
⑵当y=2时,
=75
答:至少75分钟时间内,师生不能进入教室.
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
