27.1.1 图形的相似课件
图片预览






文档简介
(共58张PPT)
27.1.1 图形的相似
人教版 九年级下
在现实生活中,我们经常见到形状相同的图形。如国旗上大小不同的五角星,还有不同尺寸同底版的相片等等。
一、 相似图形的概念
这些形状相同的图形之间,在数量关系和位置关系上有什么规律吗?
地图上的比例尺是怎样得到的?怎么才能按要求放大或缩小一张美丽的图片?
进入这一章的学习吧!
在实验和探索之后,你就会得出答案。
怎么才能按要求放大或缩小一张美丽的图片?
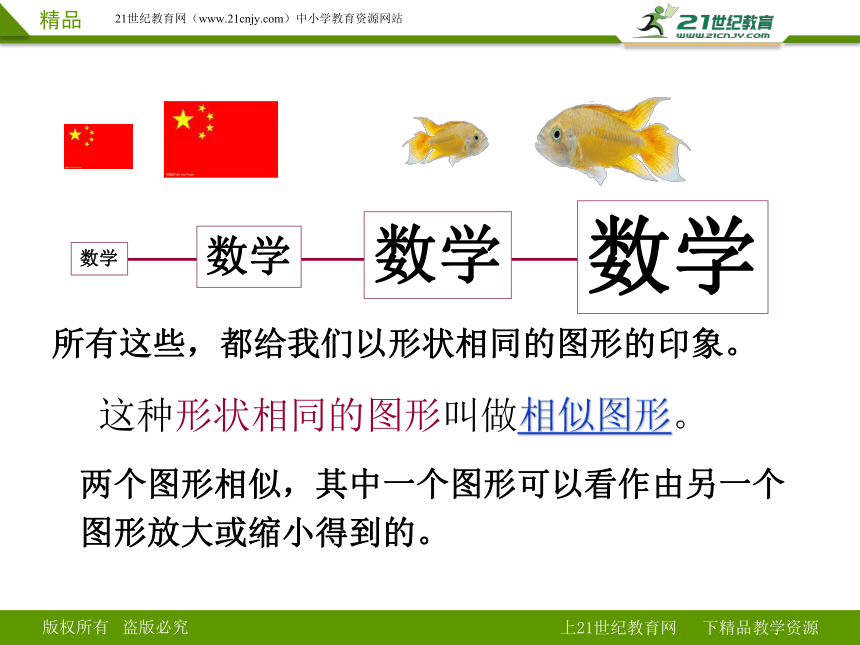
所有这些,都给我们以形状相同的图形的印象。
数学
数学
数学
数学
这种形状相同的图形叫做相似图形。
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到的。
1、下面是两两相似的几何图形的例子。
课堂练习之一
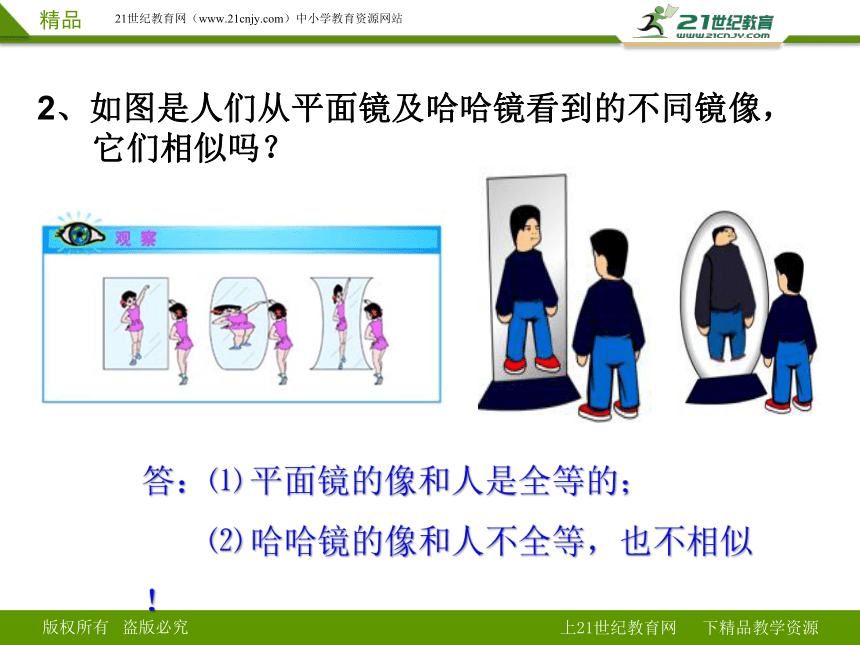
2、如图是人们从平面镜及哈哈镜看到的不同镜像,
它们相似吗?
答:⑴ 平面镜的像和人是全等的;
⑵ 哈哈镜的像和人不全等,也不相似!
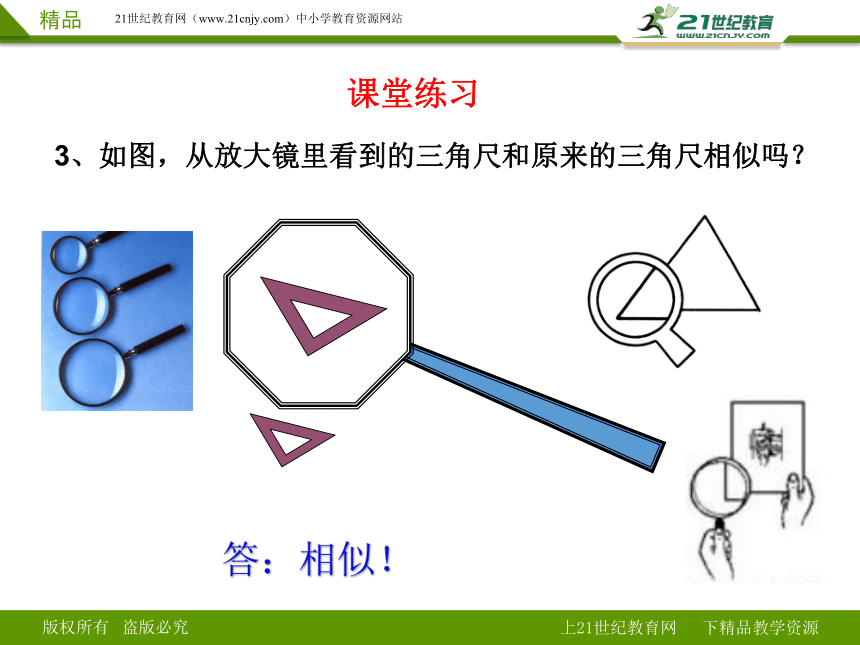
3、如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
课堂练习
答:相似!
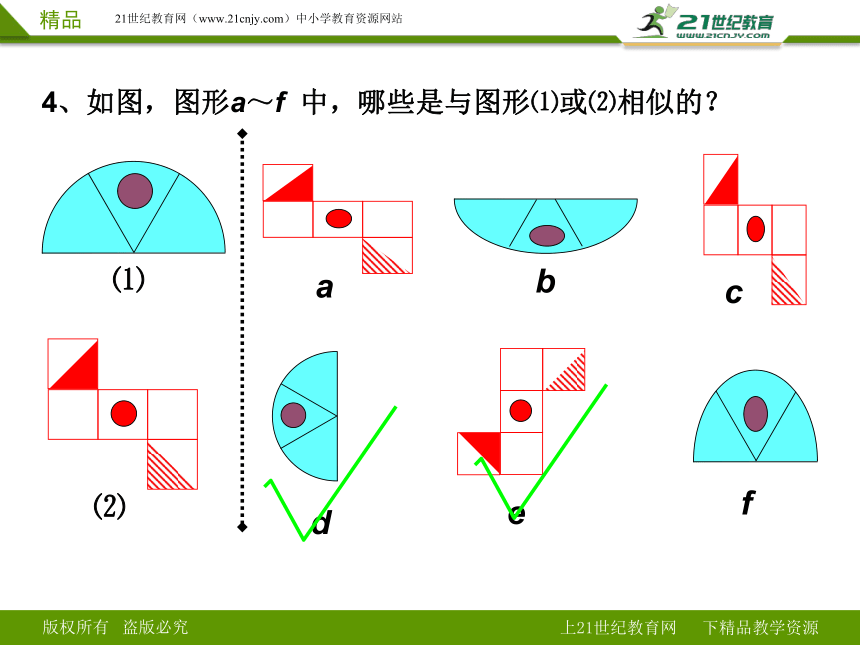
4、如图,图形a~f 中,哪些是与图形⑴或⑵相似的?
a
b
c
d
e
f
⑴
⑵
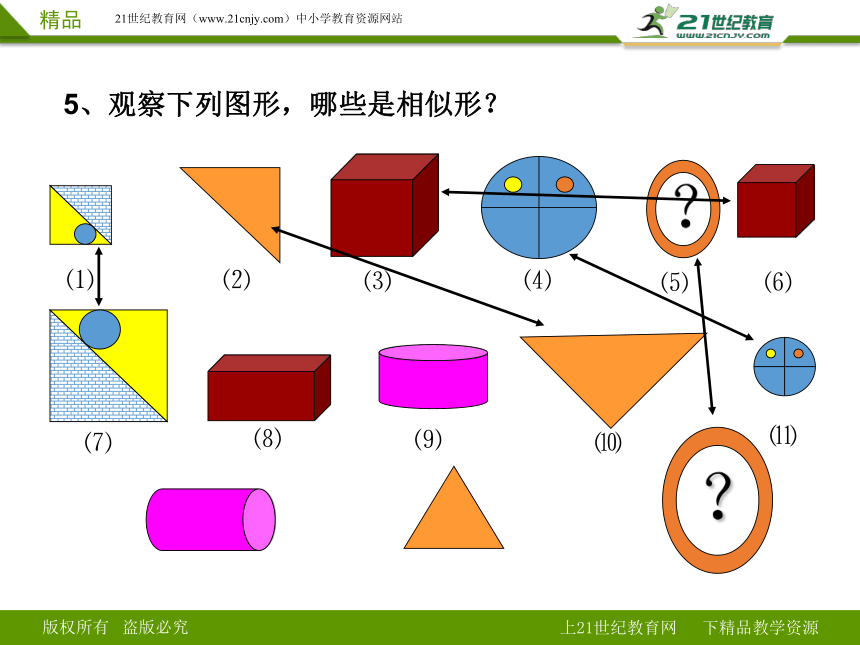
5、观察下列图形,哪些是相似形?
⑴
⑵
⑶
⑺
⑼
⑻
⑷
⑹
⑸
?
⑽
⑾
?
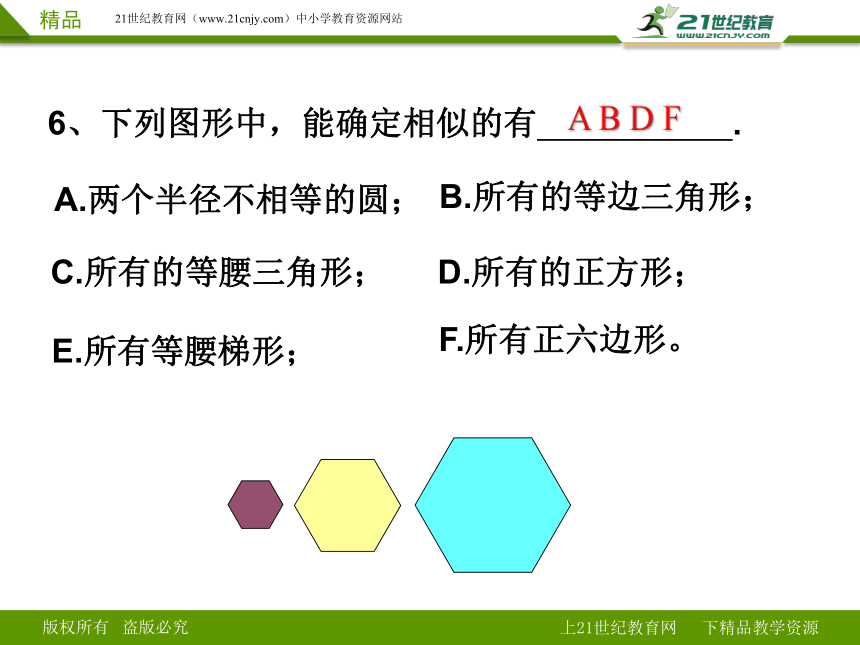
6、下列图形中,能确定相似的有 .
A.两个半径不相等的圆;
B.所有的等边三角形;
C.所有的等腰三角形;
D.所有的正方形;
E.所有等腰梯形;
F.所有正六边形。
A B D F
7、下列说法正确的是【 】
A.小明上幼儿园时的照片和初中毕业时的照片相似;
B.商店新买来的一副三角板是相似的;
C.所有的课本都是相似的;
D.国旗上的五角星都是相似的。
D
8、下列图形一定是相似图形的是【 】
A.任意两个菱形; B、任意两个正三角形;
C.两个等腰三角形; D、两个矩形。
B
9、下列说法中,错误的是【 】
A.有两个全等三角形一定是相似形;
B.两个等腰三角形一定相似;
C.两个等边三角形一定相似;
D.两个等腰直角三角形一定相似。
B
二、 相似多边形的性质
如图,△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
A
B
C
A1
B1
C1
A
B
C
A1
B1
C1
∴△ABC和△A1B1C1 相似。
∴△ABC和△A1B1C1 都是正三角形。
由于△A1B1C1是由正△ABC放大后得到的。
∴∠A=∠A1,∠B=∠B1, ∠C=∠C1
AB=BC=AC, A1B1=B1C1=A1C1
∴△ABC和△A1B1C1 都是正三角形。
∴∠A=∠A1,∠B=∠B1, ∠C=∠C1
AB=BC=AC, A1B1=B1C1=A1C1
由此说明,正三角形都是相似的。
且:⑴对应角相等。
⑵对应边的比相等。
如下图中的正六边形A1B1C1D1E1F1是由正六边形ABCDEF放大后得到的,观察这两个图形,它们的对应角又有什么关系?对应边呢?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
⑴对应角相等;
⑵对应边的比相等。
两个相似的正多边形的
⑴对应角相等;
⑵对应边的比相等。
这对于一般的相似多边形是否也成立呢?
1、相似正多边形的性质
⑴在四条线段,a,b,c,d,如果其中两条线段的比与另两条线段的比相等(如 或a∶b=c∶d即ad=bc),我们就说这四条线段是成比例线段,简称比例线段。
2、知识标签
⑵、第四比例项:若 或 a∶b=c∶d
则d叫a、b、c的第四比例项。
⑶、比例中项:若 或 a∶b=b∶c
则b叫a、c的比例中项。
⑷、比例的基本性质:
ad=bc(b≠0,d≠0)
b2=ac
⑸、合比性质
( b+d+······+n≠0 )
⑹、等比性质:
那么:
如果:
如图,是两个相似的三角形吗?它们的对应角有什么关系?对应边的比是否相等?
A
B
C
A1
B1
C1
可以用勾股定理计算各边的长度,再求它们的比。
A
B
C
A1
B1
C1
AB=
BC=
AC=
A1B1=
B1C1=
A1C1=
显然,三边的比不相等!
五边形ABCDE与五边形A′B′C′D′E′相似
记作:五边形ABCDE∽五边形A′B′C′D′E′
读作:五边形ABCDE相似于五边形A′B′C′D′E′
A
B
C
D
E
A′
B′
C′
D′
E′
如图,是两个相似的四边形吗?它们的对应角、对应边是否有相同的结论?
A
B
C
A1
B1
C1
D
D1
对于相似多边形,都有:
相似多边形对应角相等;对应边的比相等。
3、相似多边形的性质
对于相似多边形,都有:
相似多边形对应角相等;对应边的比相等。
反过来,有:
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似。
我们把相似多边形对应边的比称为相似比。
1、若 ,则x= .
2、下列各组数中,成比例的是【 】
A.-7,-5,14,5; B、-6,-8,3,4;
C.3,5,9,12; D、2,3,6,12
课堂练习之二
2.5
B
*
3、如果 x∶(x+y)=3∶5,那么x∶y=【 】
A.8∶5; B、3∶8; C.2∶3; D、3∶2
D
5x=3x+3y
2x=3y
x∶y=3∶2
*
4、把矩形对折后得到的矩形和原来的矩形相似,
那么这个矩形的长和宽的比为【 】
A.2∶1; B、4∶1; C. ∶1; D、3∶2
C
解:设原来的宽为1,长为 x ,则
x2=2
5、已知△ABC和△DEF相似,相似比为3,且
△ABC的周长为18,则△DEF的周长为【 】
A. 2; B、3; C.6; D、54
C
*
6、已知△ABC和△A1B1C1相似,相似比为2∶3,
△A1B1C1和△A2B2C2相似,相似比为5∶4,
则△ABC与△A2B2C2的相似比为【 】
6∶5; B、5∶6; C. 6∶5或5∶6; D、8∶15
B
AB∶A1B1
=2∶3
=10∶15
A1B1∶A2B2
=5∶4
=15∶12
AB∶A2B2
=10∶12
=5∶6
*
7、如图,在矩形ABCD中,AE=2ED,BF=2FC,AD=3cm,若矩形AEFB与矩形ABCD相似,则AB= cm。
A
B
C
D
E
F
1
2
x
解:设AB= x cm,则
x2=6
例1、如图,四边形ABCD和EFGH相似,
求∠α、∠β的大小和EH的长度x。
A
B
C
D
18cm
21cm
78°
83°
β
E
F
G
H
24cm
118°
α
解:四边形和ABCD和EFGH相似,
它们的对应角相等。
x
∴∠α=∠C=
解:四边形和ABCD和EFGH相似,它们的对应角相等。
∠A=∠E=
83°
118°
在四边形ABCD中,
∠β=360°-(78°+83°+118°) = 81°
四边形和ABCD和EFGH相似,
它们的对应边的比相等。
四边形和ABCD和EFGH相似,它们的对应边的比相等。
由此可得
即
解得
x=28
答:∠α=83° , ∠β=81°,EH=28cm
课堂练习之三
1、在比例尺为1∶1000 0000的地图上,量得甲、乙两地的距离是30cm,求这两地的实际距离。
解:设这两地的实际距离为xcm。
解得
x=3×108
答:这两地的实际距离为3000km。
2、如图所示的两个三角形相似吗?为什么?
5
5
10
10
解:这两个三角形相似。
因为,它们的对应角相等,对应边的比相等。
3、如图所示的两个五边形相似,求未知边a、b
c、d的长度。
7.5
9
6
a
b
3
5
2
c
d
解:由两个五边形相似,可知:
解:由两个五边形相似,可知:
5a=7.5×2
a=3
2b=3×3
b=4.5
3c=12
c=4
3d=18
d=6
3、如图所示的两个五边形相似,求未知边a、b、c、d的长度。
3
5
2
c
d
7.5
9
6
a
b
4、任意两个正方形相似吗?任意两个矩形呢?
证明你的结论。
解:⑴ 任意两个正方形相似。
证明:如图,设正方形ABCD的边长为a,
正方形EFGH的边长为b.
A
B
C
D
E
F
G
H
则所有对应角相等,都是直角
所有对应边的比都相等,都等于
∴正方形ABCD∽正方形EFGH.
4、任意两个正方形相似吗?任意两个矩形呢?
证明你的结论。
⑵ 任意两个矩形不一定相似。
①当两个矩形的长与长的比等于它们宽与宽的比时,这两个矩形相似;
②当两个矩形的长与长的比不等于它们宽与宽的比时,这两个矩形不相似;
5、如图,△ABC与△DEF相似,求未知边x、y的长度。
x
y
4
7
8
12
解:∵△ABC∽△DEF
A
B
C
D
E
F
解,得
x=6,y=3.5
6、如图,试着在方格纸中画出与原图形相似的图形,
你用的是什么方法?与同学交流一下。
7、如图,DE∥BC,求 , ,
并证明△ADE与△ABC相似。
A
B
C
D
E
2
4
5
2.5
3
9
解:⑴ 由题意,得
7、如图,DE∥BC,求 , ,
并证明△ADE与△ABC相似。
A
B
C
D
E
2
4
5
2.5
3
9
⑵ 由上可知得
∵ DE∥BC
∴∠ADE=∠B
∠AED=∠C
又∵∠A=∠A
∴△ADE∽△ABC
8、如图,矩形草坪长30m,宽20m,沿草坪四周有1m宽的环行小路,小路内外边缘所形成的两个矩形相似吗?说出你的理由。
答: 这两个矩形不相似。理由如下:
∵小路内边缘矩形的长、宽分别为:
28m、18m
∴ 对应边的比不相等,因此,这两个矩形不相似。
7、如图,已知△ABC和△ADE相似,AB=30cm,BD=18cm,BC=32cm,∠BAC=75°,∠B=40°。求⑴∠ADE和∠AED的度数;⑵DE的长。
A
B
C
D
E
解:⑴ ∵△ABC∽△ADE
∴∠ADE=∠B=40°
∠AED=∠C
=180°-75°-40°
=65°
7、如图,已知△ABC和△ADE相似,AB=30cm,BD=18cm,BC=32cm,∠BAC=75°,∠B=40°。求⑴∠ADE和∠AED的度数; ⑵DE的长。
A
B
C
D
E
⑵ ∵△ABC∽△ADE
∴ DE=12.8cm
9、如图,将一张矩形纸片沿较长的边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么原来的矩形的长宽比是多少?将这张纸再如此对折下去,得到的矩形都相似吗?
9、如图,将一张矩形纸片沿较长的边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么原来的矩形的长宽比是多少?将这张纸再如此对折下去,得到的矩形都相似吗?
解:设原矩形的宽为1,长为 x,则
x2=2
答:原矩形的长宽比为
再对折下去,得到的矩形都相似。
1、如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3,4及x,那么x的值是【 】
只有1个; B、可以有2个;
C.可以有3个; D、有无数个。
中考链接
B
*
2、如图,矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD等于【 】
A. B、 C. D、2
A
B
C
D
E
F
B
1
1
解:设AD=x
则DF=x-1
x-1
x2-x-1=0
3、(2014年浙江绍兴) 把标准纸一次又一次对开,可以得到均相似的“开纸”。 现在我们在长为 、宽为1的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是 .
x
y
*
4、如图,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF和矩形ABCO相似,其相似比为1∶4,矩形ABCO的边AB=4,BC= ,将矩形ODEF绕点O顺时针旋转一周,连接EC、EA、AC,则整个旋转过程中△ACE的最大面积为 。
A
B
C
D
E
F
O
G
E0
由BC= AB,得
∠OAC=30°,AC=8
∴ OG=
由OD=1,得
OE=2
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
27.1.1 图形的相似
人教版 九年级下
在现实生活中,我们经常见到形状相同的图形。如国旗上大小不同的五角星,还有不同尺寸同底版的相片等等。
一、 相似图形的概念
这些形状相同的图形之间,在数量关系和位置关系上有什么规律吗?
地图上的比例尺是怎样得到的?怎么才能按要求放大或缩小一张美丽的图片?
进入这一章的学习吧!
在实验和探索之后,你就会得出答案。
怎么才能按要求放大或缩小一张美丽的图片?
所有这些,都给我们以形状相同的图形的印象。
数学
数学
数学
数学
这种形状相同的图形叫做相似图形。
两个图形相似,其中一个图形可以看作由另一个图形放大或缩小得到的。
1、下面是两两相似的几何图形的例子。
课堂练习之一
2、如图是人们从平面镜及哈哈镜看到的不同镜像,
它们相似吗?
答:⑴ 平面镜的像和人是全等的;
⑵ 哈哈镜的像和人不全等,也不相似!
3、如图,从放大镜里看到的三角尺和原来的三角尺相似吗?
课堂练习
答:相似!
4、如图,图形a~f 中,哪些是与图形⑴或⑵相似的?
a
b
c
d
e
f
⑴
⑵
5、观察下列图形,哪些是相似形?
⑴
⑵
⑶
⑺
⑼
⑻
⑷
⑹
⑸
?
⑽
⑾
?
6、下列图形中,能确定相似的有 .
A.两个半径不相等的圆;
B.所有的等边三角形;
C.所有的等腰三角形;
D.所有的正方形;
E.所有等腰梯形;
F.所有正六边形。
A B D F
7、下列说法正确的是【 】
A.小明上幼儿园时的照片和初中毕业时的照片相似;
B.商店新买来的一副三角板是相似的;
C.所有的课本都是相似的;
D.国旗上的五角星都是相似的。
D
8、下列图形一定是相似图形的是【 】
A.任意两个菱形; B、任意两个正三角形;
C.两个等腰三角形; D、两个矩形。
B
9、下列说法中,错误的是【 】
A.有两个全等三角形一定是相似形;
B.两个等腰三角形一定相似;
C.两个等边三角形一定相似;
D.两个等腰直角三角形一定相似。
B
二、 相似多边形的性质
如图,△A1B1C1是由正△ABC放大后得到的,观察这两个图形,它们的对应角有什么关系?对应边呢?
A
B
C
A1
B1
C1
A
B
C
A1
B1
C1
∴△ABC和△A1B1C1 相似。
∴△ABC和△A1B1C1 都是正三角形。
由于△A1B1C1是由正△ABC放大后得到的。
∴∠A=∠A1,∠B=∠B1, ∠C=∠C1
AB=BC=AC, A1B1=B1C1=A1C1
∴△ABC和△A1B1C1 都是正三角形。
∴∠A=∠A1,∠B=∠B1, ∠C=∠C1
AB=BC=AC, A1B1=B1C1=A1C1
由此说明,正三角形都是相似的。
且:⑴对应角相等。
⑵对应边的比相等。
如下图中的正六边形A1B1C1D1E1F1是由正六边形ABCDEF放大后得到的,观察这两个图形,它们的对应角又有什么关系?对应边呢?
A
B
C
D
E
F
A1
B1
C1
D1
E1
F1
⑴对应角相等;
⑵对应边的比相等。
两个相似的正多边形的
⑴对应角相等;
⑵对应边的比相等。
这对于一般的相似多边形是否也成立呢?
1、相似正多边形的性质
⑴在四条线段,a,b,c,d,如果其中两条线段的比与另两条线段的比相等(如 或a∶b=c∶d即ad=bc),我们就说这四条线段是成比例线段,简称比例线段。
2、知识标签
⑵、第四比例项:若 或 a∶b=c∶d
则d叫a、b、c的第四比例项。
⑶、比例中项:若 或 a∶b=b∶c
则b叫a、c的比例中项。
⑷、比例的基本性质:
ad=bc(b≠0,d≠0)
b2=ac
⑸、合比性质
( b+d+······+n≠0 )
⑹、等比性质:
那么:
如果:
如图,是两个相似的三角形吗?它们的对应角有什么关系?对应边的比是否相等?
A
B
C
A1
B1
C1
可以用勾股定理计算各边的长度,再求它们的比。
A
B
C
A1
B1
C1
AB=
BC=
AC=
A1B1=
B1C1=
A1C1=
显然,三边的比不相等!
五边形ABCDE与五边形A′B′C′D′E′相似
记作:五边形ABCDE∽五边形A′B′C′D′E′
读作:五边形ABCDE相似于五边形A′B′C′D′E′
A
B
C
D
E
A′
B′
C′
D′
E′
如图,是两个相似的四边形吗?它们的对应角、对应边是否有相同的结论?
A
B
C
A1
B1
C1
D
D1
对于相似多边形,都有:
相似多边形对应角相等;对应边的比相等。
3、相似多边形的性质
对于相似多边形,都有:
相似多边形对应角相等;对应边的比相等。
反过来,有:
如果两个多边形满足对应角相等,对应边的比相等,那么这两个多边形相似。
我们把相似多边形对应边的比称为相似比。
1、若 ,则x= .
2、下列各组数中,成比例的是【 】
A.-7,-5,14,5; B、-6,-8,3,4;
C.3,5,9,12; D、2,3,6,12
课堂练习之二
2.5
B
*
3、如果 x∶(x+y)=3∶5,那么x∶y=【 】
A.8∶5; B、3∶8; C.2∶3; D、3∶2
D
5x=3x+3y
2x=3y
x∶y=3∶2
*
4、把矩形对折后得到的矩形和原来的矩形相似,
那么这个矩形的长和宽的比为【 】
A.2∶1; B、4∶1; C. ∶1; D、3∶2
C
解:设原来的宽为1,长为 x ,则
x2=2
5、已知△ABC和△DEF相似,相似比为3,且
△ABC的周长为18,则△DEF的周长为【 】
A. 2; B、3; C.6; D、54
C
*
6、已知△ABC和△A1B1C1相似,相似比为2∶3,
△A1B1C1和△A2B2C2相似,相似比为5∶4,
则△ABC与△A2B2C2的相似比为【 】
6∶5; B、5∶6; C. 6∶5或5∶6; D、8∶15
B
AB∶A1B1
=2∶3
=10∶15
A1B1∶A2B2
=5∶4
=15∶12
AB∶A2B2
=10∶12
=5∶6
*
7、如图,在矩形ABCD中,AE=2ED,BF=2FC,AD=3cm,若矩形AEFB与矩形ABCD相似,则AB= cm。
A
B
C
D
E
F
1
2
x
解:设AB= x cm,则
x2=6
例1、如图,四边形ABCD和EFGH相似,
求∠α、∠β的大小和EH的长度x。
A
B
C
D
18cm
21cm
78°
83°
β
E
F
G
H
24cm
118°
α
解:四边形和ABCD和EFGH相似,
它们的对应角相等。
x
∴∠α=∠C=
解:四边形和ABCD和EFGH相似,它们的对应角相等。
∠A=∠E=
83°
118°
在四边形ABCD中,
∠β=360°-(78°+83°+118°) = 81°
四边形和ABCD和EFGH相似,
它们的对应边的比相等。
四边形和ABCD和EFGH相似,它们的对应边的比相等。
由此可得
即
解得
x=28
答:∠α=83° , ∠β=81°,EH=28cm
课堂练习之三
1、在比例尺为1∶1000 0000的地图上,量得甲、乙两地的距离是30cm,求这两地的实际距离。
解:设这两地的实际距离为xcm。
解得
x=3×108
答:这两地的实际距离为3000km。
2、如图所示的两个三角形相似吗?为什么?
5
5
10
10
解:这两个三角形相似。
因为,它们的对应角相等,对应边的比相等。
3、如图所示的两个五边形相似,求未知边a、b
c、d的长度。
7.5
9
6
a
b
3
5
2
c
d
解:由两个五边形相似,可知:
解:由两个五边形相似,可知:
5a=7.5×2
a=3
2b=3×3
b=4.5
3c=12
c=4
3d=18
d=6
3、如图所示的两个五边形相似,求未知边a、b、c、d的长度。
3
5
2
c
d
7.5
9
6
a
b
4、任意两个正方形相似吗?任意两个矩形呢?
证明你的结论。
解:⑴ 任意两个正方形相似。
证明:如图,设正方形ABCD的边长为a,
正方形EFGH的边长为b.
A
B
C
D
E
F
G
H
则所有对应角相等,都是直角
所有对应边的比都相等,都等于
∴正方形ABCD∽正方形EFGH.
4、任意两个正方形相似吗?任意两个矩形呢?
证明你的结论。
⑵ 任意两个矩形不一定相似。
①当两个矩形的长与长的比等于它们宽与宽的比时,这两个矩形相似;
②当两个矩形的长与长的比不等于它们宽与宽的比时,这两个矩形不相似;
5、如图,△ABC与△DEF相似,求未知边x、y的长度。
x
y
4
7
8
12
解:∵△ABC∽△DEF
A
B
C
D
E
F
解,得
x=6,y=3.5
6、如图,试着在方格纸中画出与原图形相似的图形,
你用的是什么方法?与同学交流一下。
7、如图,DE∥BC,求 , ,
并证明△ADE与△ABC相似。
A
B
C
D
E
2
4
5
2.5
3
9
解:⑴ 由题意,得
7、如图,DE∥BC,求 , ,
并证明△ADE与△ABC相似。
A
B
C
D
E
2
4
5
2.5
3
9
⑵ 由上可知得
∵ DE∥BC
∴∠ADE=∠B
∠AED=∠C
又∵∠A=∠A
∴△ADE∽△ABC
8、如图,矩形草坪长30m,宽20m,沿草坪四周有1m宽的环行小路,小路内外边缘所形成的两个矩形相似吗?说出你的理由。
答: 这两个矩形不相似。理由如下:
∵小路内边缘矩形的长、宽分别为:
28m、18m
∴ 对应边的比不相等,因此,这两个矩形不相似。
7、如图,已知△ABC和△ADE相似,AB=30cm,BD=18cm,BC=32cm,∠BAC=75°,∠B=40°。求⑴∠ADE和∠AED的度数;⑵DE的长。
A
B
C
D
E
解:⑴ ∵△ABC∽△ADE
∴∠ADE=∠B=40°
∠AED=∠C
=180°-75°-40°
=65°
7、如图,已知△ABC和△ADE相似,AB=30cm,BD=18cm,BC=32cm,∠BAC=75°,∠B=40°。求⑴∠ADE和∠AED的度数; ⑵DE的长。
A
B
C
D
E
⑵ ∵△ABC∽△ADE
∴ DE=12.8cm
9、如图,将一张矩形纸片沿较长的边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么原来的矩形的长宽比是多少?将这张纸再如此对折下去,得到的矩形都相似吗?
9、如图,将一张矩形纸片沿较长的边的中点对折,如果得到的两个矩形都和原来的矩形相似,那么原来的矩形的长宽比是多少?将这张纸再如此对折下去,得到的矩形都相似吗?
解:设原矩形的宽为1,长为 x,则
x2=2
答:原矩形的长宽比为
再对折下去,得到的矩形都相似。
1、如果一个直角三角形的两条边长分别是6和8,另一个与它相似的直角三角形边长分别是3,4及x,那么x的值是【 】
只有1个; B、可以有2个;
C.可以有3个; D、有无数个。
中考链接
B
*
2、如图,矩形ABCD中,AB=1,在BC上取一点E,沿AE将△ABE向上折叠,使B点落在AD上的F点,若四边形EFDC与矩形ABCD相似,则AD等于【 】
A. B、 C. D、2
A
B
C
D
E
F
B
1
1
解:设AD=x
则DF=x-1
x-1
x2-x-1=0
3、(2014年浙江绍兴) 把标准纸一次又一次对开,可以得到均相似的“开纸”。 现在我们在长为 、宽为1的矩形纸片中,画两个小矩形,使这两个小矩形的每条边都与原矩形纸的边平行,或小矩形的边在原矩形的边上,且每个小矩形均与原矩形纸相似,然后将它们剪下,则所剪得的两个小矩形纸片周长之和的最大值是 .
x
y
*
4、如图,矩形ODEF的一边落在矩形ABCO的一边上,并且矩形ODEF和矩形ABCO相似,其相似比为1∶4,矩形ABCO的边AB=4,BC= ,将矩形ODEF绕点O顺时针旋转一周,连接EC、EA、AC,则整个旋转过程中△ACE的最大面积为 。
A
B
C
D
E
F
O
G
E0
由BC= AB,得
∠OAC=30°,AC=8
∴ OG=
由OD=1,得
OE=2
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
