27.1.2 相似三角形的预备定理课件
图片预览




文档简介
(共27张PPT)
27.1.2 相似三角形的预备定理
人教版 九年级下
在相似多边形中,最简单的就是相似三角形
在△ABC和△A/B/C/中
如果:∠A=∠A/,∠B=∠B/,∠C=∠C/
定义:如果两个三角形的对应角相等,对应边的比相等.
那么这两个三角形相似。
我们说:△ABC∽△A/B/C/
一、复习引入
并且:
△ABC∽△A/B/C/
△ABC与△A/B/C/的相似比为 k
△A/B/C/ 与△ABC的相似比为
曾记得:三角形全等的定义是
今天我们将学习研究,判定两个三角形相似的最简便的方法!
所有的对应角相等,对应边相等的两个三角形全等。
SSS,SAS,ASA,AAS,HL
三角形全等的判定定理共有四个:
对于三角形相似也有简便方法吗?
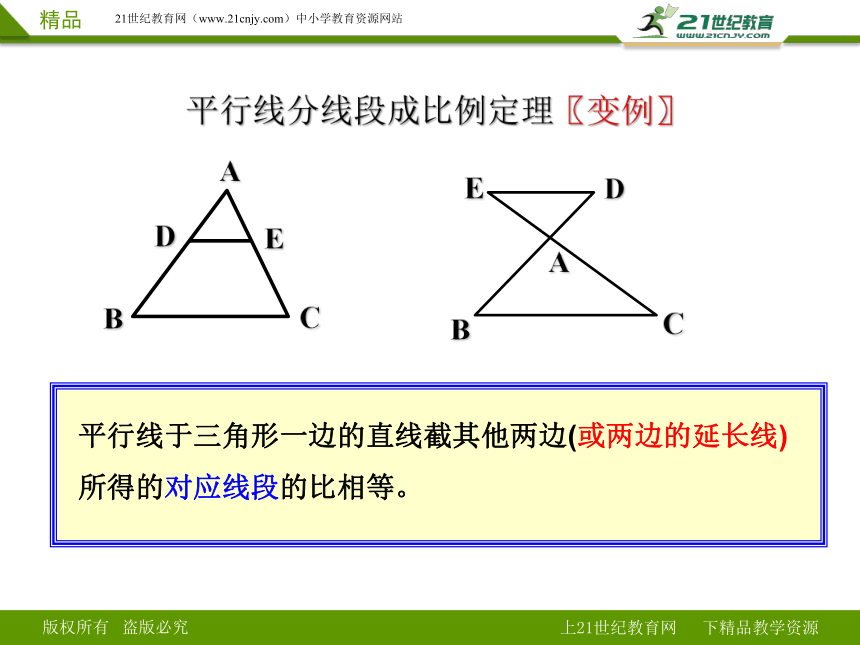
平行线分线段成比例定理〖变例〗
平行线于三角形一边的直线截其他两边(或两边的延长线)
所得的对应线段的比相等。
A
B
C
D
E
A
B
C
D
E
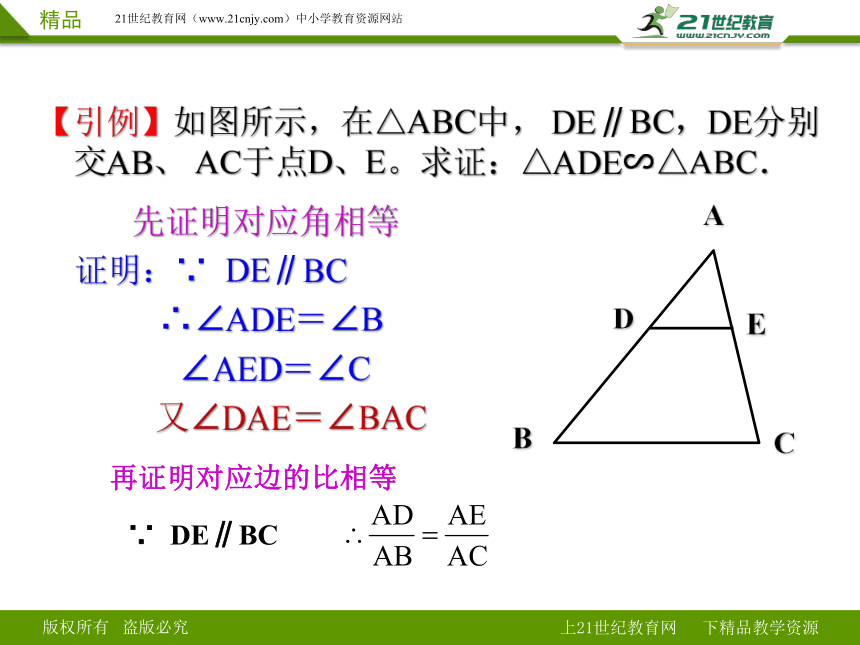
【引例】如图所示,在△ABC中, DE∥BC,DE分别
交AB、 AC于点D、E。求证:△ADE∽△ABC.
A
B
C
D
E
证明:∵ DE∥BC
又∠DAE=∠BAC
∴∠ADE=∠B
∠AED=∠C
先证明对应角相等
∵ DE∥BC
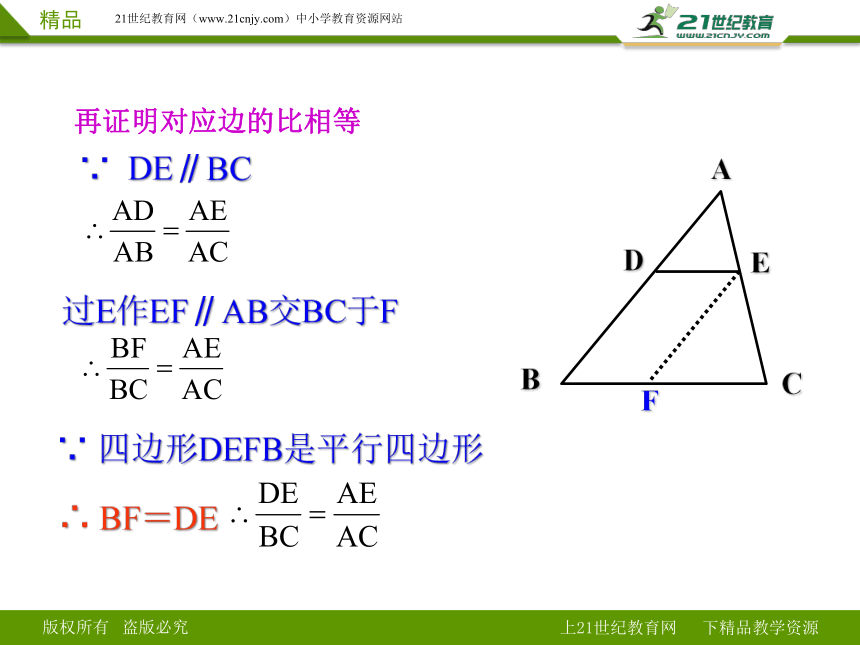
再证明对应边的比相等
A
B
C
D
E
∵ DE∥BC
F
过E作EF∥AB交BC于F
∵ 四边形DEFB是平行四边形
∴ BF=DE
再证明对应边的比相等
A
B
C
D
E
F
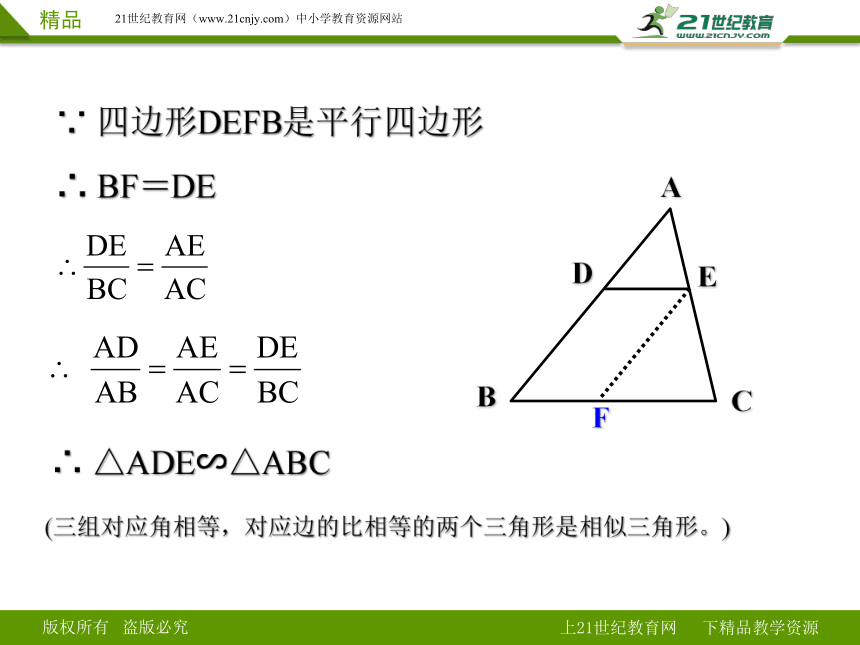
∵ 四边形DEFB是平行四边形
∴ BF=DE
∴ △ADE∽△ABC
(三组对应角相等,对应边的比相等的两个三角形是相似三角形。)
相似三角形的 预备定理
A
B
C
D
E
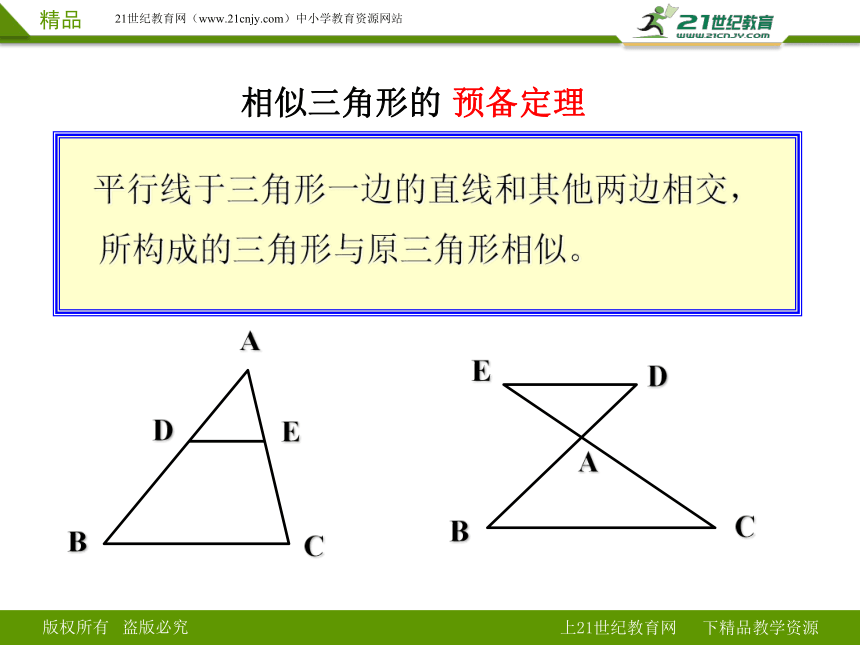
平行线于三角形一边的直线和其他两边相交,
所构成的三角形与原三角形相似。
A
B
C
D
E
预备定理的书写方法
A
B
C
D
E
A
B
C
D
E
∵ DE∥BC
∴ △ADE∽△ABC
【注】这是证明相似三角形的最简单的方法!
1.如图,BD是△ABC的角平分线,点E在AB上,DE∥BC
AE=4,BC=8,求DE的长。
A
B
C
D
E
解: ∵ DE∥BC
∴ BE=DE
∴ ∠2=∠3
1
2
3
∵ ∠1=∠2
∴ ∠1=∠3
课堂练习 (共8道大题)
4
8
1.如图,BD是△ABC的角平分线,点E在AB上,DE∥BC,AE=4,BC=8,求DE的长。
4
8
∵ DE∥BC
∴ △AED∽△ABC
设DE=x,则
解,得 x1=4,x2=-8(舍去)
答:DE的长是4。
A
B
C
D
E
1
2
3
∴ BE=DE
x
x
2.如图,已知DE∥BC,DF∥AC,AD=4,BD=8,DE=5,求线段BF的长。
A
B
C
D
E
F
4
8
5
解: ∵ DE∥BC,DF∥AC
∴四边形DECF是平行四边形
∴ FC=DE=5
∵ DE∥BC
∴ △ADE∽△ABC
5
∴ △ADE∽△ABC
∴ BF=10
2.如图,已知DE∥BC,DF∥AC,AD=4,BD=8,DE=5,求线段BF的长。
A
B
C
D
E
F
4
8
5
5
3.如图,已知四边形BDFE是菱形,BD=2·DC,
且DC=4,求AE的长。
A
B
C
D
E
F
解:∵ 四边形BDFE是菱形
∴ EF∥BC
BE=EF=BD
∴ △AEF∽△ABC
=8
BC=BD+DC
=8+4
=12
8
8
8
4
3.如图,已知四边形BDFE是菱形,BD=2·DC,
且DC=4,求AE的长。
A
B
C
D
E
F
BC=BD+DC=8+4=12
∴ AE=16
8
8
8
4
4、E是□ABCD的BC边上一点, AE交BD于F,
且BE∶EC=4∶5,求 的值。
A
B
C
D
E
F
解:∵ □ABCD
∴ AD∥BC,BC=AD
∴ △BEF∽△DAF
A
B
C
D
E
F
∴ △BEF∽△DAF
∵ BE∶EC=4∶5
4、E是□ABCD的BC边上一点, AE交BD于F,
且BE∶EC=4∶5,求 的值。
4、E是□ABCD的BC边上一点,AE交BD于F,
且BE∶EC=4∶5,求 的值。
A
B
C
D
E
F
5、在锐角△ABC中,D是AC上一点,且 ,
G是BD中点,连结AG并延长,交BC于E,
⑴求 的值,⑵求 的值。
A
B
C
G
D
E
F
解:⑴过点D作DF∥AE交BC于F
∵ G是BD中点
∴ BD=2BG
A
B
C
G
D
E
F
∴ BD=2BG
∵DF∥AE
∴ FC=2EF
∴ BF=2BE=2EF
1
1
2
⑴求 的值.
A
B
C
G
D
E
F
1
1
2
⑵ 求 的值.
=4
6、E是□ABCD的BC边延长线上一点,AE交DC于F,交BD于G 。求证:AG2=GF·GE
A
B
C
D
E
F
G
解:∵ □ABCD
∴ AD∥BC ,AB∥DC
∴ △ADG∽△EBG, △BGA∽△DGF
∴ AG2=GF·GE
7、如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连接BE交AC于点F,BE的延长线交CD的延长线于点G,
求证:
A
B
C
D
E
F
G
解:∵ AD∥BC
∴ △GED∽△GBC
∵ AE=DE
8、如图,已知菱形ABCD内接于△AEF,AE=5cm,
AF=4cm,求菱形的边长。
A
B
C
D
E
F
解:设菱形的边长为xcm.
由菱形可知:DC∥AE
∴ △FDC∽△FAE
菱形的边长为
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
27.1.2 相似三角形的预备定理
人教版 九年级下
在相似多边形中,最简单的就是相似三角形
在△ABC和△A/B/C/中
如果:∠A=∠A/,∠B=∠B/,∠C=∠C/
定义:如果两个三角形的对应角相等,对应边的比相等.
那么这两个三角形相似。
我们说:△ABC∽△A/B/C/
一、复习引入
并且:
△ABC∽△A/B/C/
△ABC与△A/B/C/的相似比为 k
△A/B/C/ 与△ABC的相似比为
曾记得:三角形全等的定义是
今天我们将学习研究,判定两个三角形相似的最简便的方法!
所有的对应角相等,对应边相等的两个三角形全等。
SSS,SAS,ASA,AAS,HL
三角形全等的判定定理共有四个:
对于三角形相似也有简便方法吗?
平行线分线段成比例定理〖变例〗
平行线于三角形一边的直线截其他两边(或两边的延长线)
所得的对应线段的比相等。
A
B
C
D
E
A
B
C
D
E
【引例】如图所示,在△ABC中, DE∥BC,DE分别
交AB、 AC于点D、E。求证:△ADE∽△ABC.
A
B
C
D
E
证明:∵ DE∥BC
又∠DAE=∠BAC
∴∠ADE=∠B
∠AED=∠C
先证明对应角相等
∵ DE∥BC
再证明对应边的比相等
A
B
C
D
E
∵ DE∥BC
F
过E作EF∥AB交BC于F
∵ 四边形DEFB是平行四边形
∴ BF=DE
再证明对应边的比相等
A
B
C
D
E
F
∵ 四边形DEFB是平行四边形
∴ BF=DE
∴ △ADE∽△ABC
(三组对应角相等,对应边的比相等的两个三角形是相似三角形。)
相似三角形的 预备定理
A
B
C
D
E
平行线于三角形一边的直线和其他两边相交,
所构成的三角形与原三角形相似。
A
B
C
D
E
预备定理的书写方法
A
B
C
D
E
A
B
C
D
E
∵ DE∥BC
∴ △ADE∽△ABC
【注】这是证明相似三角形的最简单的方法!
1.如图,BD是△ABC的角平分线,点E在AB上,DE∥BC
AE=4,BC=8,求DE的长。
A
B
C
D
E
解: ∵ DE∥BC
∴ BE=DE
∴ ∠2=∠3
1
2
3
∵ ∠1=∠2
∴ ∠1=∠3
课堂练习 (共8道大题)
4
8
1.如图,BD是△ABC的角平分线,点E在AB上,DE∥BC,AE=4,BC=8,求DE的长。
4
8
∵ DE∥BC
∴ △AED∽△ABC
设DE=x,则
解,得 x1=4,x2=-8(舍去)
答:DE的长是4。
A
B
C
D
E
1
2
3
∴ BE=DE
x
x
2.如图,已知DE∥BC,DF∥AC,AD=4,BD=8,DE=5,求线段BF的长。
A
B
C
D
E
F
4
8
5
解: ∵ DE∥BC,DF∥AC
∴四边形DECF是平行四边形
∴ FC=DE=5
∵ DE∥BC
∴ △ADE∽△ABC
5
∴ △ADE∽△ABC
∴ BF=10
2.如图,已知DE∥BC,DF∥AC,AD=4,BD=8,DE=5,求线段BF的长。
A
B
C
D
E
F
4
8
5
5
3.如图,已知四边形BDFE是菱形,BD=2·DC,
且DC=4,求AE的长。
A
B
C
D
E
F
解:∵ 四边形BDFE是菱形
∴ EF∥BC
BE=EF=BD
∴ △AEF∽△ABC
=8
BC=BD+DC
=8+4
=12
8
8
8
4
3.如图,已知四边形BDFE是菱形,BD=2·DC,
且DC=4,求AE的长。
A
B
C
D
E
F
BC=BD+DC=8+4=12
∴ AE=16
8
8
8
4
4、E是□ABCD的BC边上一点, AE交BD于F,
且BE∶EC=4∶5,求 的值。
A
B
C
D
E
F
解:∵ □ABCD
∴ AD∥BC,BC=AD
∴ △BEF∽△DAF
A
B
C
D
E
F
∴ △BEF∽△DAF
∵ BE∶EC=4∶5
4、E是□ABCD的BC边上一点, AE交BD于F,
且BE∶EC=4∶5,求 的值。
4、E是□ABCD的BC边上一点,AE交BD于F,
且BE∶EC=4∶5,求 的值。
A
B
C
D
E
F
5、在锐角△ABC中,D是AC上一点,且 ,
G是BD中点,连结AG并延长,交BC于E,
⑴求 的值,⑵求 的值。
A
B
C
G
D
E
F
解:⑴过点D作DF∥AE交BC于F
∵ G是BD中点
∴ BD=2BG
A
B
C
G
D
E
F
∴ BD=2BG
∵DF∥AE
∴ FC=2EF
∴ BF=2BE=2EF
1
1
2
⑴求 的值.
A
B
C
G
D
E
F
1
1
2
⑵ 求 的值.
=4
6、E是□ABCD的BC边延长线上一点,AE交DC于F,交BD于G 。求证:AG2=GF·GE
A
B
C
D
E
F
G
解:∵ □ABCD
∴ AD∥BC ,AB∥DC
∴ △ADG∽△EBG, △BGA∽△DGF
∴ AG2=GF·GE
7、如图,梯形ABCD中,AD∥BC,点E是边AD的中点,连接BE交AC于点F,BE的延长线交CD的延长线于点G,
求证:
A
B
C
D
E
F
G
解:∵ AD∥BC
∴ △GED∽△GBC
∵ AE=DE
8、如图,已知菱形ABCD内接于△AEF,AE=5cm,
AF=4cm,求菱形的边长。
A
B
C
D
E
F
解:设菱形的边长为xcm.
由菱形可知:DC∥AE
∴ △FDC∽△FAE
菱形的边长为
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
