28.1 锐角三角函数课件
图片预览








文档简介
(共40张PPT)
28.1 锐角三角函数
人教版 九年级下
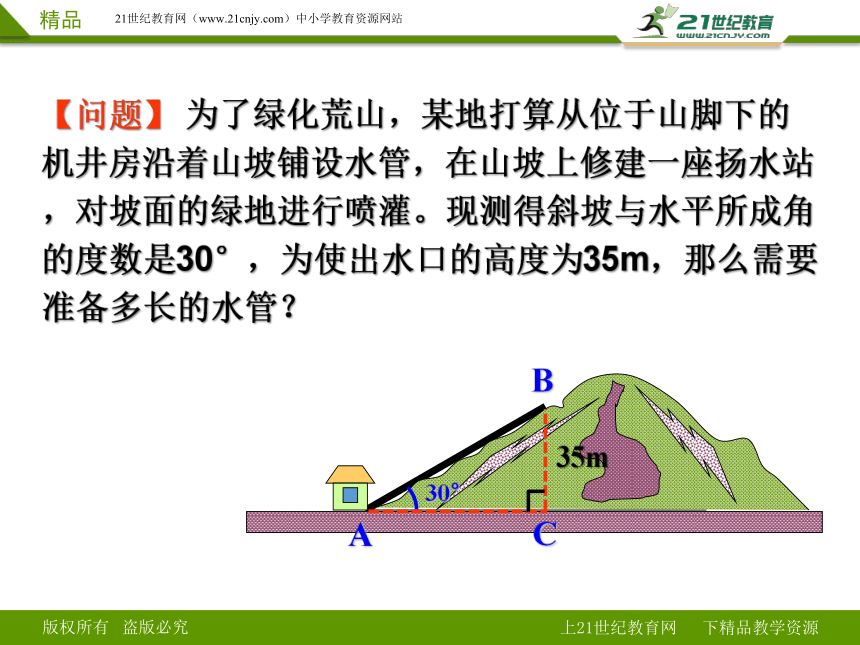
【问题】 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌。现测得斜坡与水平所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
B
C
A
30°
35m
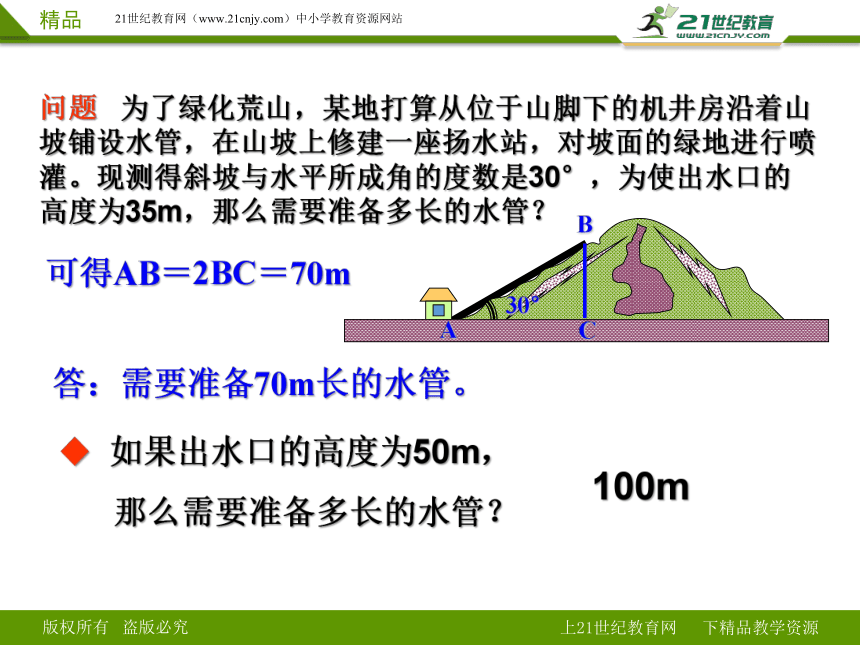
问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌。现测得斜坡与水平所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
B
C
A
30°
这个问题可归为:
在Rt△ABC中,
∠A=30°,BC=35m,求AB。
根据“在直角三角形中,30°角所对的边等于斜边的一半”
即
问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌。现测得斜坡与水平所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
可得AB=2BC=70m
答:需要准备70m长的水管。
如果出水口的高度为50m,
那么需要准备多长的水管?
100m
B
C
A
30°
如果出水口的高度为50m,
那么需要准备多长的水管?
如果出水口的高度为60m,
那么需要准备多长的水管?
如果出水口的高度为80m,
那么需要准备多长的水管?
100m
120m
160m
在上面求AB (所需水管的长度) 的过程中,我们用到了下面的结论:
在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 。
思考
如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比 ,你能得出什么结论?
A
B
C
解:∵ AB2=AC2+BC2
∴ AB2=2BC2
AC=BC
如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比 ,你能得出什么结论?
解:∵ AB2=AC2+BC2
∴ AB2=2BC2
AC=BC
A
B
C
一般地,当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值呢?
在一个直角三角形中,如果一个锐角等于45°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 。
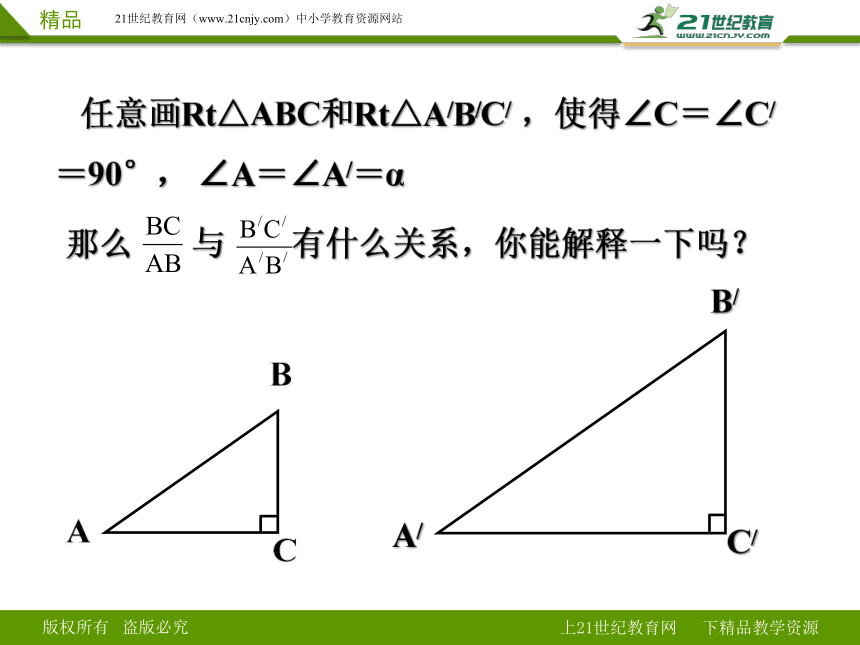
任意画Rt△ABC和Rt△A/B/C/ ,使得∠C=∠C/
=90°, ∠A=∠A/=α
那么 与 有什么关系,你能解释一下吗?
A
B
C
A/
B/
C/
A
B
C
A/
B/
C/
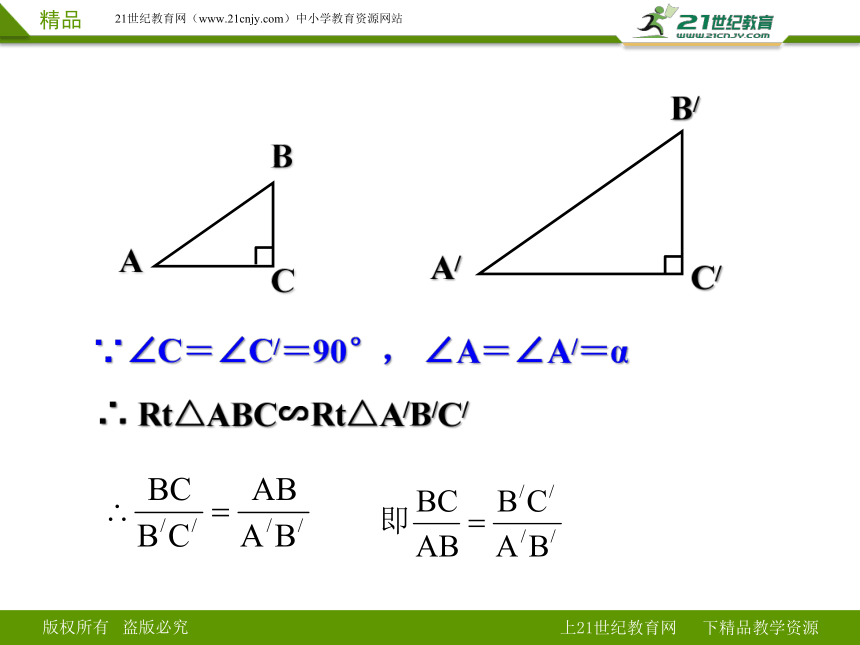
∵∠C=∠C/=90°, ∠A=∠A/=α
∴ Rt△ABC∽Rt△A/B/C/
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值。
结论
三角函数的定义
在Rt△ABC中,∠C=90°,我们把∠A的对边
与斜边的比叫做∠A的正弦(sine)[ \sain ]
记作 sinA
例如,⑴ 当∠A=30°时,我们有
sinA=sin30°=
⑵ 当∠A=45°时,我们有
sinA=sin45°=
⑶ 当∠A=60°时,我们有
sinA=sin60°=
例1、如图,在Rt△ABC中,∠C=90°,
求sinA和sinB的值。
A
B
C
3
4
图⑴
A
B
C
5
13
图⑵
例1、如图,在Rt△ABC,∠C=90°求sinA和sinB的值。
A
B
C
3
4
图⑴
解: 在Rt△ABC中
=5
因此 sinA=
sinB=
例1、如图,在Rt△ABC,∠C=90°求sinA和sinB的值。
解: 在Rt△ABC中
=12
因此 sinA=
sinB=
A
B
C
5
13
图⑵
1、根据下图,求sinA和sinB的值。
A
B
C
3
5
图⑴
练习
解: 在Rt△ABC中
因此 sinA=
sinB=
探究:如图,在Rt△ABC中,∠C=90°,当锐角A确定时, ∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?
A
B
C
∠A的对边
∠A的邻边
斜边
A
B
C
∠A的对边
∠A的邻边
斜边
类似于正弦的情况,在图中,当锐角A的大小确定时,∠A的邻边与斜边的比、 ∠A的对边与邻边的比也分别是确定的。
我们把∠A的邻边与斜边的比叫做∠A的余弦(cosine)[\ksain ]
记作 cosA
我们把∠A的对边与邻边的比叫做∠A的正切(tangent)
记作 tanA
A
B
C
∠A的对边
∠A的邻边
斜边
B
A
C
a
b
c
锐角A的正弦、余弦、正切都叫做∠A的锐角
三角函数:即sinA、 cosA、tanA。
A
C
6
B
例2、如图,在Rt△ABC中,∠C=90°,BC=6
,求cosA、tanB的值。
解:
∴AB=
=8
8
10
例2、如图,在Rt△ABC,∠C=90°,BC=6
,求cosA、tanB的值。
A
C
6
B
8
10
1、分别求出下列直角三角形中两个锐角的正弦值
余弦和正切值。
A
C
3
B
2
A
C
12
B
13
课堂练习
图⑴
图⑵
1、分别求出下列直角三角形中两个锐角的正弦值、余弦和正切值。
解:
=5
A
C
12
B
13
图⑴
解:
1、分别求出下列直角三角形中两个锐角的正弦值、余弦和正切值。
A
C
3
B
2
2、在Rt△ABC中,如果各边都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化
答:锐角A的正弦值、余弦值和正切值
都是一个固定的值,不会变化。
3、如图,在Rt△ABC中, ∠C=90°,AC=8,
, 求sinA、cosB的值。
A
C
B
8
AC=8
解:
A
C
B
8
AC=8
解:
=10
6
10
思考:两块三角尺中有几个不同的锐角?分别求出
这几个锐角的正弦值,余弦值和正切值。
A
C
B
A
B
C
30°,45°,60°角的正弦值,
余弦值和正切值如下表:
1
2
1
1
30° 45° 60°
sinα
cosα
tanα
1
A
C
B
1
2
A
B
C
1
1
例3 求下列各式的值:
⑴ cos260°+sin260°
⑵
解: ⑴ 原式=
=1
⑵ 原式=
=0
练习 求下列各式的值:
⑴ 1- 2sin30°cos30°
解: ⑴ 原式=
⑵ 原式=
⑵ 3tan30°-tan45°+2sin60°
⑶
解:⑶ 原式=
=2
例4、⑴如图,在Rt△ABC中, ∠C=90°,
AB= ,BC= ,求∠A的度数。
A
B
C
解:
∴ ∠A=45°
例4、⑵如图,在Rt△ABC中, ∠C=90°,
BC= ,AC= ,求∠A、∠B的度数。
A
B
C
解:
∴ ∠A=30°
∠B=90°-∠A=60°
例4、⑶如图,已知圆锥的高OA等于圆锥的
底面半径的 倍,求α。
α
A
B
O
解:
∴ ∠α=60°
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
28.1 锐角三角函数
人教版 九年级下
【问题】 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌。现测得斜坡与水平所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
B
C
A
30°
35m
问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌。现测得斜坡与水平所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
B
C
A
30°
这个问题可归为:
在Rt△ABC中,
∠A=30°,BC=35m,求AB。
根据“在直角三角形中,30°角所对的边等于斜边的一半”
即
问题 为了绿化荒山,某地打算从位于山脚下的机井房沿着山坡铺设水管,在山坡上修建一座扬水站,对坡面的绿地进行喷灌。现测得斜坡与水平所成角的度数是30°,为使出水口的高度为35m,那么需要准备多长的水管?
可得AB=2BC=70m
答:需要准备70m长的水管。
如果出水口的高度为50m,
那么需要准备多长的水管?
100m
B
C
A
30°
如果出水口的高度为50m,
那么需要准备多长的水管?
如果出水口的高度为60m,
那么需要准备多长的水管?
如果出水口的高度为80m,
那么需要准备多长的水管?
100m
120m
160m
在上面求AB (所需水管的长度) 的过程中,我们用到了下面的结论:
在一个直角三角形中,如果一个锐角等于30°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 。
思考
如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比 ,你能得出什么结论?
A
B
C
解:∵ AB2=AC2+BC2
∴ AB2=2BC2
AC=BC
如图,任意画一个Rt△ABC,使∠C=90°,∠A=45°,计算∠A的对边与斜边的比 ,你能得出什么结论?
解:∵ AB2=AC2+BC2
∴ AB2=2BC2
AC=BC
A
B
C
一般地,当∠A取其他一定度数的锐角时,它的对边与斜边的比是否也是一个固定值呢?
在一个直角三角形中,如果一个锐角等于45°,那么不管三角形的大小如何,这个角的对边与斜边的比值都等于 。
任意画Rt△ABC和Rt△A/B/C/ ,使得∠C=∠C/
=90°, ∠A=∠A/=α
那么 与 有什么关系,你能解释一下吗?
A
B
C
A/
B/
C/
A
B
C
A/
B/
C/
∵∠C=∠C/=90°, ∠A=∠A/=α
∴ Rt△ABC∽Rt△A/B/C/
在直角三角形中,当锐角A的度数一定时,不管三角形的大小如何,∠A的对边与斜边的比也是一个固定值。
结论
三角函数的定义
在Rt△ABC中,∠C=90°,我们把∠A的对边
与斜边的比叫做∠A的正弦(sine)[ \sain ]
记作 sinA
例如,⑴ 当∠A=30°时,我们有
sinA=sin30°=
⑵ 当∠A=45°时,我们有
sinA=sin45°=
⑶ 当∠A=60°时,我们有
sinA=sin60°=
例1、如图,在Rt△ABC中,∠C=90°,
求sinA和sinB的值。
A
B
C
3
4
图⑴
A
B
C
5
13
图⑵
例1、如图,在Rt△ABC,∠C=90°求sinA和sinB的值。
A
B
C
3
4
图⑴
解: 在Rt△ABC中
=5
因此 sinA=
sinB=
例1、如图,在Rt△ABC,∠C=90°求sinA和sinB的值。
解: 在Rt△ABC中
=12
因此 sinA=
sinB=
A
B
C
5
13
图⑵
1、根据下图,求sinA和sinB的值。
A
B
C
3
5
图⑴
练习
解: 在Rt△ABC中
因此 sinA=
sinB=
探究:如图,在Rt△ABC中,∠C=90°,当锐角A确定时, ∠A的对边与斜边的比就随之确定,此时,其他边之间的比是否也确定了呢?为什么?
A
B
C
∠A的对边
∠A的邻边
斜边
A
B
C
∠A的对边
∠A的邻边
斜边
类似于正弦的情况,在图中,当锐角A的大小确定时,∠A的邻边与斜边的比、 ∠A的对边与邻边的比也分别是确定的。
我们把∠A的邻边与斜边的比叫做∠A的余弦(cosine)[\ksain ]
记作 cosA
我们把∠A的对边与邻边的比叫做∠A的正切(tangent)
记作 tanA
A
B
C
∠A的对边
∠A的邻边
斜边
B
A
C
a
b
c
锐角A的正弦、余弦、正切都叫做∠A的锐角
三角函数:即sinA、 cosA、tanA。
A
C
6
B
例2、如图,在Rt△ABC中,∠C=90°,BC=6
,求cosA、tanB的值。
解:
∴AB=
=8
8
10
例2、如图,在Rt△ABC,∠C=90°,BC=6
,求cosA、tanB的值。
A
C
6
B
8
10
1、分别求出下列直角三角形中两个锐角的正弦值
余弦和正切值。
A
C
3
B
2
A
C
12
B
13
课堂练习
图⑴
图⑵
1、分别求出下列直角三角形中两个锐角的正弦值、余弦和正切值。
解:
=5
A
C
12
B
13
图⑴
解:
1、分别求出下列直角三角形中两个锐角的正弦值、余弦和正切值。
A
C
3
B
2
2、在Rt△ABC中,如果各边都扩大2倍,那么锐角A的正弦值、余弦值和正切值有什么变化
答:锐角A的正弦值、余弦值和正切值
都是一个固定的值,不会变化。
3、如图,在Rt△ABC中, ∠C=90°,AC=8,
, 求sinA、cosB的值。
A
C
B
8
AC=8
解:
A
C
B
8
AC=8
解:
=10
6
10
思考:两块三角尺中有几个不同的锐角?分别求出
这几个锐角的正弦值,余弦值和正切值。
A
C
B
A
B
C
30°,45°,60°角的正弦值,
余弦值和正切值如下表:
1
2
1
1
30° 45° 60°
sinα
cosα
tanα
1
A
C
B
1
2
A
B
C
1
1
例3 求下列各式的值:
⑴ cos260°+sin260°
⑵
解: ⑴ 原式=
=1
⑵ 原式=
=0
练习 求下列各式的值:
⑴ 1- 2sin30°cos30°
解: ⑴ 原式=
⑵ 原式=
⑵ 3tan30°-tan45°+2sin60°
⑶
解:⑶ 原式=
=2
例4、⑴如图,在Rt△ABC中, ∠C=90°,
AB= ,BC= ,求∠A的度数。
A
B
C
解:
∴ ∠A=45°
例4、⑵如图,在Rt△ABC中, ∠C=90°,
BC= ,AC= ,求∠A、∠B的度数。
A
B
C
解:
∴ ∠A=30°
∠B=90°-∠A=60°
例4、⑶如图,已知圆锥的高OA等于圆锥的
底面半径的 倍,求α。
α
A
B
O
解:
∴ ∠α=60°
谢谢
21世纪教育网(www.21cnjy.com)中小学教育资源网站
有大把优质资料?一线名师?一线教研员?
赶快加入21世纪教育网名师合作团队吧!!月薪过万不是梦!!
详情请看:http://www.21cnjy.com/zhaoshang/
