2.1 多边形（2）同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
2.1 多边形（2）同步练习
　班级__________姓名____________总分___________
本节应掌握和应用的知识点
１．多边形的内角的一边与另一边的反向延长 ( http: / / www.21cnjy.com )线所组成的角叫作这个多边形的一个外角,在多边形的每个顶点处取 一个 外角,它们的和叫做这个多边形的外角和．
２．任意多边形的外角和等于３６０°．
３．三角形具有稳定性,四边形具有不稳定性．
4.平面图形镶嵌
（1）平面图形镶嵌的定义：用形状，大小完全 ( http: / / www.21cnjy.com )相同的一种或几种平面图形进行拼接．彼此之间不留空隙，不重叠地铺成一片，这就是平面图形的镶嵌．
（2）正多边形镶嵌有三个条件限制：①边长相等；②顶点公共；③在一个顶点处各正多边形的内角之和为360°．
判断一种或几种图形是否能够镶嵌，只要看一看拼在同一顶点处的几个角能否构成周角，若能构成360°，则说明能够进行平面镶嵌，反之则不能．21世纪教育网版权所有
基础知识和能力拓展精练
一、选择题
1．一个正多边形的内角和为540°，则这个正多边形的每一个外角等于（　　）
A. 108° B. 90° C. 72° D. 60°
2．一个多边形的内角和比它的外角和的4倍少180°，这个多边形的边数是（ ）
A. 5 B. 6 C. 9 D. 8
3．一个多边形的每一个顶点处取一个外角，这些外角中最多有钝角（ ）
A. 1个 B. 2个 C. 3个 D. 4个
4．如果一个正多边形的一个内角和它相邻外角的比是3∶1，那么这个多边形是（　　）
A. 正六边形 B. 正八边形 C. 正十边形 D. 正十二边形
5．若n边形的内角和与外角和的比为8∶2，则n为（　　）
A. 7 B. 8 C. 9 D. 10
6．如果一个正多边形的一个外角为30°，那么这个正多边形的边数是（　　）
A. 6 B. 11 C. 12 D. 18
7．过多边形的一个顶点可以作7条对角线，则此多边形的内角和是外角和的（　　）
A. 4倍 B. 5倍 C. 6倍 D. 3倍
8．某班同学对《多边形的内角和与外角和》的 ( http: / / www.21cnjy.com )内容进行激烈地讨论，小丽说：“多边形的边数每增加1，则内角和增加180°”，小钟说：“多边形的边数每增加1，则外角和增加180°”，小刚说：“多边形的内角和不小于其外角和”，小华说：“只要是凸多边形，不管有几边，其外角和都是360°”．你认为正确的是( )21cnjy.com
A. 小丽和小华 B. 小钟和小刚 C. 小刚和小华 D. 以上都不对
9．如图，已知正五边形ABCDE，AF∥CD，交DB的延长线于点F，则∠DFA等于（　　）
( http: / / www.21cnjy.com )
A. 30° B. 36° C. 45° D. 32°
10．由图中所表示的已知角的度数，可知∠α的度数为（ ）
( http: / / www.21cnjy.com )
A. 80° B. 70° C. 60° D. 50°
二、填空题
11．已知一个多边形的内角和与外角和的差为1080°，则这个多边形是______边形．
12．如图所示，小华从A点 ( http: / / www.21cnjy.com )出发，沿直线前进10米后左转24，再沿直线前进10米，又向左转24°，…，照这样走下去，他第一次回到出发地A点时，一共走的路程是_______.
( http: / / www.21cnjy.com )
13．已知：如图，求∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＋∠8____________．
( http: / / www.21cnjy.com )
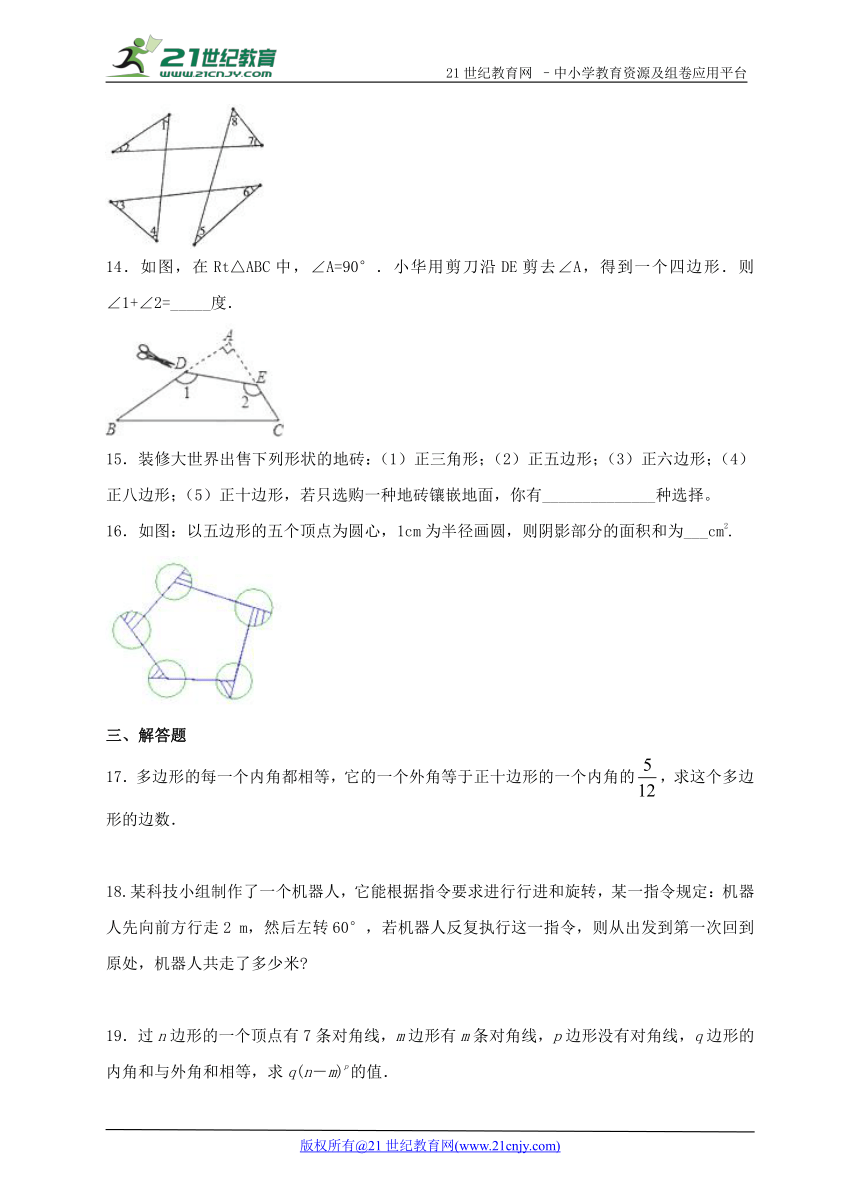
14．如图，在Rt△ABC中，∠A=90°．小华用剪刀沿DE剪去∠A，得到一个四边形．则∠1+∠2=_____度．21·cn·jy·com
( http: / / www.21cnjy.com ) ( http: / / www.21cnjy.com )
15．装修大世界出售下列形状的地砖：（ ( http: / / www.21cnjy.com )1）正三角形；（2）正五边形；（3）正六边形；（4）正八边形；（5）正十边形，若只选购一种地砖镶嵌地面，你有______________种选择。
16．如图：以五边形的五个顶点为圆心，1cm为半径画圆，则阴影部分的面积和为___cm2.
( http: / / www.21cnjy.com )
三、解答题
17．多边形的每一个内角都相等，它的一个外角等于正十边形的一个内角的，求这个多边形的边数．
18.某科技小组制作了一个机器人， ( http: / / www.21cnjy.com )它能根据指令要求进行行进和旋转，某一指令规定：机器人先向前方行走2 m，然后左转60°，若机器人反复执行这一指令，则从出发到第一次回到原处，机器人共走了多少米 21·世纪*教育网
19．过n边形的一个顶点有7条对角线，m边形有m条对角线，p边形没有对角线，q边形的内角和与外角和相等，求q(n－m)p的值．2-1-c-n-j-y
20．如图，六边形ABCDEF的内角都相等，CF∥AB.
(1)求∠FCD的度数；
(2)求证：AF∥CD.
( http: / / www.21cnjy.com )
21．已知一个n边形的每一个内角都等于150°。
（1）求n；
（2）求这个n边形的内角和；
（3）从这个n边形的一个顶点出发，可以画出几条对角线？
22．如图，CE是△ABC的外角∠ACD的平分线，且CE交BA的延长线于点E，
证明：∠BAC=∠B+2∠E
( http: / / www.21cnjy.com )
23．如图，在中， ， 平分， 平分外角， 与交于点，求的度数．
( http: / / www.21cnjy.com )
24．(1)如图①②,试研究其中∠1、∠2与∠3、∠4之间的数量关系；
( http: / / www.21cnjy.com )
(2)如果我们把∠1、∠2称为四边形的外角,那么请你用文字描述上述的关系式;
(3)用你发现的结论解决下列问题:
如图,AE、DE分别是四边形ABCD的外角∠NAD、∠MDA的平分线,∠B+∠C=240°,求∠E的度数.【出处：21教育名师】
( http: / / www.21cnjy.com )
参考答案
1．C
【解析】试题解析：设此多边形为n边 ( http: / / www.21cnjy.com )形，根据题意得：180（n﹣2）=540，解得：n=5，故这个正多边形的每一个外角等于：360°÷5 =72°．故选C．【版权所有：21教育】
2．C
【解析】设所求多边形边数为n，
则(n 2) 180°=4×360° 180°，
解得n=9.
故选：C.
3．C
【解析】∵多边形的外角和等于360 ，
∴外角中钝角最多有3个。
故选C.
4．B
【解析】设这个多边形的边数是n,则 EMBED Equation.DSMT4 ∶ =3∶1，解得：n=8,故选B.
5．D
【解析】因为一个多边形的内角和与外角和之比为8：2，外角和是360度，因而内角和是180×8度，
又n边形的内角和是(n-2) 180°，
则有(n-2) 180=180×8，
解得：n=10．
那么此多边形的边数为10．
故选D．
6．C
【解析】试题解析：这个正多边形的边数：360°÷30°=12，故选C．
7．A
【解析】∵过多边形的一个顶点共有7条对角线，
∴该多边形边数为10，
∴（10﹣2） 180°=1440°，
∴这个多边形的内角和为1440°，
又∵多边形的外角和为360°，
∴1440÷360=4．
故选A．
点睛：根据从多边形的一个顶点可以作对角线的条数公式（n-3）求出边数，再由多边形的内角和和外角和公式即可求解. 2·1·c·n·j·y
8．A
【解析】根据多边形内角和公式（n-2） 18 ( http: / / www.21cnjy.com )0 （n≥3）且n为整数）可得小丽的说法正确；根据多边形的外角和定理及多边形的外角和等于360°可知小钟的说法错误；由三角形的内角和为180°，外角和为360°，可得小刚的说法错误；根据多边形的外角和定理：多边形的外角和等于360°，可知小华的说法正确.所以说法正确的是小丽和小华，故选A．
点睛：本题主要考查了多边形 ( http: / / www.21cnjy.com )的内角和与外角和，熟知多边形的内角和公式（n-2） 180 （n≥3）且n为整数），外角和为360°是解题的关键.．21教育名师原创作品
9．B
【解析】 ,
.
∵AF∥CD，
.
故选B.
10．D
【解析】∵多边形的外角和为360°，且已知三个外角的度数分别是120°、70°、120°，
∴∠α＝（360－120－70－120）°＝50°；
故选D。
11．十．
【解析】根据题意，得（n﹣2） 180=1080+360，解得：n=10．所以这个多边形是十边形．
12．150米
【解析】∵多边形的外角和为360°，而每一个外角为24°，
∴多边形的边数为360°÷24°=15，
∴小明一共走了：15×10=150米，
故答案为：150米.
【点睛】本题考查多边形的内角和计算公式，多边形的外角和．关键是根据多边形的外角和及每一个外角都为24°求边数．【来源：21cnj*y.co*m】
13．360°
【解析】解：如图，∠1+ ( http: / / www.21cnjy.com )∠2=∠9，∠3+∠4=∠10，∠5+∠6=∠11，∠7+∠8=∠12，四边形的外角和等于360°，∴∠9+∠10+∠11+∠12=360°，∴∠1＋∠2＋∠3＋∠4＋∠5＋∠6＋∠7＋∠8=360°．故答案为：360°．www-2-1-cnjy-com
( http: / / www.21cnjy.com )
14．270
【解析】∵∠A=90°，
∴∠B+∠C=90.
∵∠B+∠C+∠1+∠2=360°，
∴∠1+∠2=360° 90°=270°.
故答案为：270.
15．2
【解析】(1)正三角形的每个内角是60°,能整除360°，6个能组成镶嵌；
(2)正五方形的每个内角是108°,不能整除360°，不能组成镶嵌；
(3)正六边形的每个内角是120°,能整除360°，3个能组成镶嵌；
(4)正八边形每个内角是135°,不能整除360°，不能镶嵌；
(5)正十边形每个内角是144°,不能整除360°，不能镶嵌；
故若只选购其中某一种地砖镶嵌地面，可供选择的地砖共有2种。
故答案为：2.
点睛：此题主要考查了平面镶嵌，用一种正 ( http: / / www.21cnjy.com )多边形的镶嵌应符合一个内角度数能整除360°.由镶嵌的条件知，判断一种图形是否能够镶嵌，只要看一看正多边形的内角度数是否能整除360°，能整除的可以平面镶嵌，反之则不能．【来源：21·世纪·教育·网】
16．∏
【解析】∵多边形外角和等于360°，
∴阴影部分的面积等于一个圆的面积，
.
17．6
【解析】分析：先求出正十边形的一个内角，再根据n边形的一个外角等于正十边形的一个内角的，求出n边形的一个外角，用360÷n边形的一个外角即可求解.
本题解析：
正10边形的内角：(10-2)×180°÷10=144°
多边形的外角：144°×5/12=60°
多边形的内角：180°-60°=120°
正多边形的边数为n
(n-2)×180°/n=120°
(180°-120°)n=360°
n=6
18．机器人共走了12 m.
【解析】分析：第一次回到原处正好转了360°，正好构成一个正六边形，先理解题目意思，再去看关键字来思考问题，来解决问题，最终得出答案．21*cnjy*com
本题解析：
机器人转了一周共360度，360°÷60°=6，共走了6次，机器人走了6×2=12米．
故答案为：12米．
点睛：考查了多边形内角与外角，本题是一 ( http: / / www.21cnjy.com )个实际问题，要理解“回到原处”就是转了360度，我们平时要多做这种类型的题目，学会抓住关键词即可快速得到正确答案．
19．500
【解析】分析：若过n边形的一个顶点有7条对角线，则n=10；m边形有m条对角线，即得到方程m(m-3)=m，解得m=5；P边形没有对角线，只有三角形没有对角线，因而P=3；q边形的内角和与外角和相等，内角和与外角和相等的只有四边形，因而q=4．代入代数式就可以求出代数式的值．
本题解析：
∵n边形从一个顶点发出的对角线有n－3条， ∴n=7+3=10，
∵m边形有m条对角线 , ∴m(m-3)=m，解之得：m=5；
∵ P边形没有对角线 ,∴P=3
∵q边形的内角和与外角和相等 ,∴q=4
∴q(n-m)p=4×=4×=500
故答案为：500
20．（1）60°（2）证明见解析
【解析】试题分析：（1）先求六边形 ( http: / / www.21cnjy.com )ABCDEF的每个内角的度数，根据平行线的性质可求∠B+∠BCF=180°，再根据四边形的内角和是360°，求∠FCD的度数，从而求解．
（2）先根据四边形内角和求出∠AFC=60°，再根据平行线的判定即可求解．
试题解析：(1)解：∵六边形ABCDEF的内角相等，∴∠B＝∠A＝∠BCD＝120°.
∵CF∥AB，∴∠B＋∠BCF＝180°，∴∠BCF＝60°，∴∠FCD＝60°.
(2)证明：∵CF∥AB，∴∠A＋∠AFC＝180°，∴∠AFC＝180°－120°＝60°，∴∠AFC＝∠FCD，∴AF∥CD.www.21-cn-jy.com
点睛：此题主要考查了多边形内角与外角和平 ( http: / / www.21cnjy.com )行线的判定，正确识别“三线八角”中的同位角、内错角、同旁内角是正确答题的关键，不能遇到相等或互补关系的角就误认为具有平行关系，只有同位角相等、内错角相等、同旁内角互补，才能推出两被截直线平行．
21．12；1800°；9.
【解析】分析：（1）首先求出外角度数 ( http: / / www.21cnjy.com )，再用360°除以外角度数可得答案．（2）利用内角度数150°×内角的个数即可；（3）根据n边形从一个顶点出发可引出（n-3）条对角线可得答案．
本题解析：
（1）∵每一个内角都等于150°，
∴每一个外角都等于180°﹣150°=30°，
∴边数n=360°÷30°=12；
（2）内角和：12×150°=1800°；
（3）从一个顶点出发可做对角线的条数：12﹣3=9．
点睛: 此题主要考查了多边形内和、外角和,对角线，关键是掌握各知识点的计算公式.
22．证明见解析.
【解析】【试题分析】在△BCE中，利用 ( http: / / www.21cnjy.com )外角的性质，得∠1=∠B+∠E；利用角平分线的性质得，∠1=∠2；在△ACE中，利用外角的性质，得∠BAC=∠E+∠2，因为∠1=∠2，得∠BAC=∠E+∠1=∠E+∠B+∠E=∠B+2∠E．得证.21教育网
【试题解析】
在△BCE中，∠1=∠B+∠E，
∵CE是△ABC的外角∠ACD的角平分线，
∴∠1=∠2，
在△ACE中，∠BAC=∠E+∠2=∠E+∠B+∠E=∠B+2∠E，
即：∠BAC=∠B+2∠E．
( http: / / www.21cnjy.com )
【方法点睛】本题目是一道证明题，主要是运用三角形外角的性质来证明.两次利用外角的性质，注意从不同的角度观察图形是解决问题的关键.
23．45o
【解析】试题分析：设∠ABC=x°，再根据三角形外角的性质得出∠BAD=∠B+∠C=90°+x°，根据AF平分外角∠BAD可知∠DAF= ∠BAD=（90°+x°），根据对顶角的性质得出∠EAG=∠DAF=（90°+x°），根据BE平分∠ABC可知∠CBE=∠ABC=x°，即可得出∠AGE的度数．
试题解析：
设,
平分,
,
是的外角,
,
平分,
,
是的外角,
,
.
24．(1)∠1+∠2=∠3+∠4；(2)四边形的任意两个外角的和等于与它们不相邻的两个内角的和；(3) 60°.21*cnjy*com
【解析】试题分析：（1）根据四 ( http: / / www.21cnjy.com )边形的内角和等于360°用∠5＋∠6表示出∠3＋∠4，再根据平角的定义用∠5＋∠6表示出∠1＋∠2，即可得解；
（2）从外角的定义考虑解答；
（3）根据（1）的结论求出∠MDA＋∠NAD，再根据角平分线的定义求出∠ADE＋∠DAE，然后利用三角形的内角和定理列式进行计算即可得解．
试题解析：
（1）∵∠3、∠4、∠5、∠6是四边形的四个内角，
∴∠3＋∠4＋∠5＋∠6＝360°.
∴∠3＋∠4＝360°－(∠5＋∠6).
∵∠1＋∠5＝180°，∠2＋∠6＝180°，
∴∠1＋∠2＝360°－(∠5＋∠6).
∴∠1＋∠2＝∠3＋∠4.
（2）四边形的任意两个外角的和等于与它们不相邻的两个内角的和.
（3）∵∠B＋∠C＝240°，
∴∠MDA＋∠NAD＝240°.
∵AE、DE分别是∠NAD、∠MDA的平分线，
∴∠ADE＝∠MDA，∠DAE＝∠NAD.
∴∠ADE＋∠DAE＝ (∠MDA＋∠NAD)＝120°.
∴∠E＝180°－(∠ADE＋∠DAE)＝60°.
点睛：本题考查了多边形的内角和公式，平角的定义，角平分线的定义，整体思想的利用是解题的关键．
( http: / / www.21cnjy.com )
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)