2.3 中心对称和中心对称图形同步练习
文档属性
| 名称 | 2.3 中心对称和中心对称图形同步练习 |

|
|
| 格式 | doc | ||
| 文件大小 | 414.5KB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 湘教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2018-02-27 18:43:20 | ||
图片预览



文档简介
21世纪教育网 –中小学教育资源及组卷应用平台
2.3 中心对称和中心对称图形同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.把一个图形绕着点O旋转180°,能够与另一个图形完全重合,那么就说这两个图形关于点O对称或中心对称,点O叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
2.成中心对称的两个图形,对称点的连线都经过 对称中心,而且被对称中心平分,中心对称的两个图形是全等图形 .
基础知识和能力拓展精练
一、单选题
1.下列图形中,是中心对称图形的是( ).
A. B. C. D.
2.△ABC和△AˊBˊCˊ关于点O对称,下列结论不正确的是( ).
A. AO=AˊO B. AB∥AˊBˊ C. CO=BO D. ∠BAC=∠BˊAˊCˊ
3.用四块形如的正方形瓷砖拼成如下四种图案,其中成中心对称图形的是( ).
A. ①② B. ②③ C. ②④ D. ①④
4.下列四边形:①平行四边形;②矩形;③菱形;④正方形.其中,是中心对称图形,而不是轴对称图形的有( )个.
A. 0 B. 1 C. 2 D. 3
二、填空题
5.关于点O成中心对称的两个四边形ABCD和DEFG,AD、BE、CF、DG都过______.
6.关于中心对称的两个图形对应线段__________________.
7.关于中心对称的两个图形,对称点的连线经过__________.
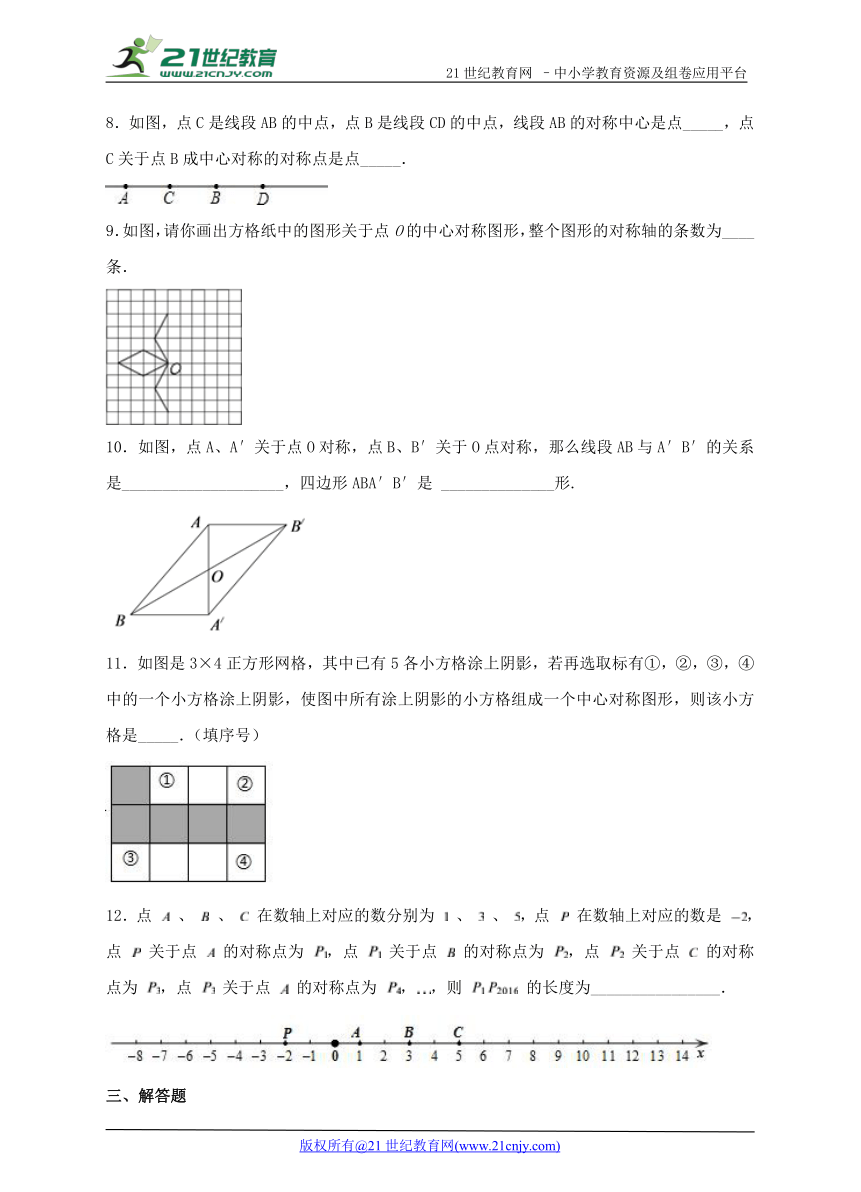
8.如图,点C是线段AB的中点,点B是线段CD的中点,线段AB的对称中心是点_____,点C关于点B成中心对称的对称点是点_____.
9.如图,请你画出方格纸中的图形关于点O的中心对称图形,整个图形的对称轴的条数为____条.
10.如图,点A、A′关于点O对称,点B、B′关于O点对称,那么线段AB与A′B′的关系是____________________,四边形ABA′B′是 ______________形.
11.如图是3×4正方形网格,其中已有5各小方格涂上阴影,若再选取标有①,②,③,④中的一个小方格涂上阴影,使图中所有涂上阴影的小方格组成一个中心对称图形,则该小方格是_____.(填序号)
12.点 、 、 在数轴上对应的数分别为 、 、 ,点 在数轴上对应的数是 ,点 关于点 的对称点为 ,点 关于点 的对称点为 ,点 关于点 的对称点为 ,点 关于点 的对称点为 ,,则 的长度为________________.
三、解答题
13.两个图形成中心对称和中心对称图形有什么区别?
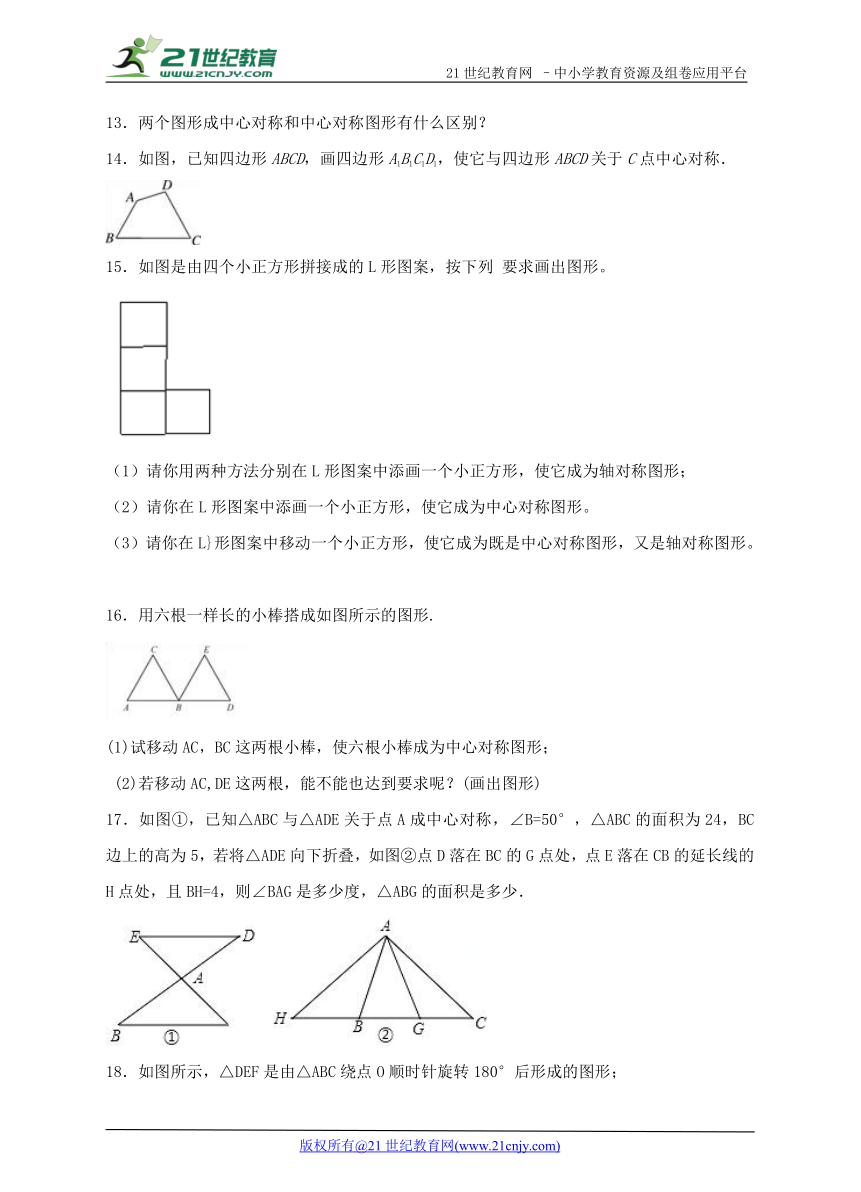
14.如图,已知四边形ABCD,画四边形A1B1C1D1,使它与四边形ABCD关于C点中心对称.
15.如图是由四个小正方形拼接成的L形图案,按下列 要求画出图形。
(1)请你用两种方法分别在L形图案中添画一个小正方形,使它成为轴对称图形;
(2)请你在L形图案中添画一个小正方形,使它成为中心对称图形。
(3)请你在L}形图案中移动一个小正方形,使它成为既是中心对称图形,又是轴对称图形。
16.用六根一样长的小棒搭成如图所示的图形.
(1)试移动AC,BC这两根小棒,使六根小棒成为中心对称图形;
(2)若移动AC,DE这两根,能不能也达到要求呢?(画出图形)
17.如图①,已知△ABC与△ADE关于点A成中心对称,∠B=50°,△ABC的面积为24,BC边上的高为5,若将△ADE向下折叠,如图②点D落在BC的G点处,点E落在CB的延长线的H点处,且BH=4,则∠BAG是多少度,△ABG的面积是多少.
18.如图所示,△DEF是由△ABC绕点O顺时针旋转180°后形成的图形;
(1)请你指出图中所有相等的线段;
(2)图中哪些三角形可以被看成是关于点O成中心对称关系?
19.如图所示,AD是△ABC的边BC的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
20.已知如图所示,△AOB与△COD关于点O成中心对称,连接BC,AD.
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15 cm2,求四边形ABCD的面积.
参考答案
1.A
【解析】根据中心对称的定义可知只有A选项符合,故选A.
2.C
【解析】因为只有对称点到对称中心的距离相等,所以C选项是错误的
故选C.
3.D
【解析】根据中心对称图形的概念,可知第①④是中心对称图形.
故选:D.
4.B
【解析】试题解析:①平行四边形,是中心对称图形,而不是轴对称图形;
②矩形,是中心对称图形,也是轴对称图形;
③菱形,是中心对称图形,也是轴对称图形;
④正方形,是中心对称图形,也是轴对称图形.
综上所述,是中心对称图形,而不是轴对称图形的只有平行四边形1个.
故选B.
点睛:根据中心对称图形和轴对称图形的概念对各图形分析判断即可得解.
5.点O
【解析】对应点的连线经过对称中心.
故答案:点O.
【方法点睛】本题目是一道考查成中心对称图形的性质,每对对应点的连线都经过对称中心,且被对称中心平分.
6.相等
【解析】关于中心对称的两个图形对应线段长度是相等的.
故答案:相等.
7.对称中心
【解析】关于中心对称的两个图形,对称点的连线经过对称中心.
故答案:对称中心.
8. C D
【解析】根据中心对称图形的对称中心的定义,点C是线段AB的中点,点B是线段CD的中点,线段AB的对称中心是点C;点C关于点B成中心对称的对称点是点D.
故答案为:C;D.
9.4
【解析】如图所示,图形中的虚线是对称轴,所以对称轴有4条.
故答案为4.
10. 平行且相等 平行四边形
【解析】∵点A、A′关于点O对称,点B、B′关于O点对称,
∴OA=OA′,OB=OB′,
∴四边形ABA′B′是平行四边形,
∴AB=A′B′,AB∥A′B′.
故答案为:平行且相等;平行四边.
11.④
【解析】解:若标有①的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成的图形不是中心对称图形;
若标有②的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个轴对称图形;
若标有③的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个轴对称图形;
若标有④的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个中心对称图形;
故答案是:④.
12.
【解析】先根据轴对称的性质找出对应边表示的数字,然后找出其中的规律,根据规律确定出表示的数,从而求得问题的答案.
解:点P关于点A的对称点P1表示的数数4;点P1关于点B的对称点P2表示的数数2;
点P2关于点C的对称点P3表示的数数8;点P3关于点A的对称点P4表示的数数-6;
点P4关于点B的对称点P5表示的数数12;点P5关于点C的对称点P6表示的数数-2;
点P6关于点A的对称点P7表示的数数4;....
2016÷6=336.所以P2016表示数为-2,所以P1 P2016=6.
【点睛】抓住对称性,寻找Pn数字规律,再根据周期算出P2016表示的数.
13.见解析
【解析】【试题分析】注意区分好成中心对称和中心对称图形的定义.
【试题解析】
前者是指具有某种特性(绕一点旋转180度后能与原图重合)的一个图形;后者是指两个图形之间,若其中某一个图形绕一点旋转180度后能与另一个图形重合,则称这两个图形之间成中心对称.
【方法点睛】本题目是一道考查成中心对称和中心对称图形的区别,重点是从定义上加以剖析.
14.见解析
【解析】试题分析:分别画出A、B、C、D各点关于点C的对称点,然后顺次连接即可.
解:四边形A1B1C1D1如图所示.
15.(1)见解析; (2)见解析; (3)见解析;
【解析】试题分析:
(1)根据原图结构,可按下列方法添加一个小正方形可使整个图形成为轴对称图形,①在下面左侧添一个小正方形;②在下面右侧添一个小正方形;③在上面右侧添一个小正方形;
(2)根据原图结构,在上面左侧添一个小正方形可使整个图形成为中心对称图形;
(3)根据原图结构,可按下列方法移动一个小正方形,可使整个图形成为中心对称图形,①将下面右侧的小正方形移到第一列的下面;②将第一列最上面的小正方形移到第二列的上面.
试题解析:
(1)按下图在的方式添加一个小正方形,整个图形是轴对称图形:
(2)按下图中的方式添加一个小正方形后整个图形是中心对称图形:
(3)按下图中的方式移动一个小正方形后整个图形是中心对称图形:
16.(1)图形见解析;
(2) 图形见解析.
【解析】试题分析:根据中心对称图形的概念求解.本题△ABC沿AB翻折可使六根小棒成为中心对称图形;移动AC、DE这两根,使它们与BC、BE沿AD翻折的图形分别重合即可.
试题解析:解:(1)如图:
(2)能,如图:
.
点睛:掌握中心对称图形的概念,判断中心对称图形的关键是要寻找对称中心,旋转180度后两部分重合.
17.∠BAG=80°,面积是14
【解析】试题分析:根据中心对称的性质和折叠的性质计算即可,同时运用了三角形的面积公式.
试题解析:依题意有AD=AB=AG,AE=AH=AC.
又∠B=50°,则∠BAG=180°-50°×2=80°;
作AD⊥BC于D,根据三角形的面积公式得到BC=9.6.
根据等腰三角形的三线合一,
可以证明CG=BH=4,则BG=5.6.
根据三角形的面积公式得△ABG的面积是14.
18.(1) AB=DE,AC=DF,BC=EF,AO=DO,BO=EO,CO=FO;(2)△ABC与△DEF,△ABO与△DEO,△ACO与△DFO,△BCO与△EFO.
【解析】【试题分析】
(1)根据中心对称图形的性质得,对应线段线段——AB=DE,AC=DF,BC=EF,对应点到旋转中心的距离相等——AO=DO,BO=EO,CO=FO;
(2)根据成中心对称图形的定义,得:△ABC与△DEF,△ABO与△DEO,△ACO与△DFO,△BCO与△EFO.
【试题解析】
(1)图中相等的线段有:AB=DE,AC=DF,BC=EF,AO=DO,BO=EO,CO=FO;
(2)图中关于点O成中心对称的三角形有:△ABC与△DEF,△ABO与△DEO,△ACO与△DFO,△BCO与△EFO.
【方法点睛】本题目是一道关于中心对称图形的性质的问题,成中心对称的两个图形,他们的对应点到旋转中心的距离相等,每对对应边相等.
19.(1)图形见解析.
(2)1【解析】试题分析:延长AD使AD=DE,再连接DE、CE即可得到三角形ECD,则△ECD与△ABD成中心对称.(2)△ECD与△ABD成中心对称.所以AB=CE=10,所以在△ACE中,12-10(1)如图,△DCE为所求.
(2) 因为△ECD与△ABD成中心对称.所以AB=CE=10,所以在△ACE中,12-1020.(1)证明见解析;(2)60 cm2.
【解析】试题分析:根据成中心对称图形的性质知OA=OC,OB=OD.根据平行四边形对角线互相平分,所以可以得到四边形ABCD为平行四边形;△AOB的面积为15 cm2,则△ABC面积等于△AOB面积的2倍,因为点O为平行四边形的中心,所以△ABC的高等于△AOB高的2倍,所以S△ABC =30,所以四边形ABCD的面积是60.
(1)∵AOB与△COD关于点O成中心对称,∴OA=OC,OB=OD.
∴四边形ABCD为平行四边形.
(2)四边形ABCD的面积为60 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
2.3 中心对称和中心对称图形同步练习
班级__________姓名____________总分___________
本节应掌握和应用的知识点
1.把一个图形绕着点O旋转180°,能够与另一个图形完全重合,那么就说这两个图形关于点O对称或中心对称,点O叫做对称中心,这两个图形中的对应点叫做关于中心的对称点.
2.成中心对称的两个图形,对称点的连线都经过 对称中心,而且被对称中心平分,中心对称的两个图形是全等图形 .
基础知识和能力拓展精练
一、单选题
1.下列图形中,是中心对称图形的是( ).
A. B. C. D.
2.△ABC和△AˊBˊCˊ关于点O对称,下列结论不正确的是( ).
A. AO=AˊO B. AB∥AˊBˊ C. CO=BO D. ∠BAC=∠BˊAˊCˊ
3.用四块形如的正方形瓷砖拼成如下四种图案,其中成中心对称图形的是( ).
A. ①② B. ②③ C. ②④ D. ①④
4.下列四边形:①平行四边形;②矩形;③菱形;④正方形.其中,是中心对称图形,而不是轴对称图形的有( )个.
A. 0 B. 1 C. 2 D. 3
二、填空题
5.关于点O成中心对称的两个四边形ABCD和DEFG,AD、BE、CF、DG都过______.
6.关于中心对称的两个图形对应线段__________________.
7.关于中心对称的两个图形,对称点的连线经过__________.
8.如图,点C是线段AB的中点,点B是线段CD的中点,线段AB的对称中心是点_____,点C关于点B成中心对称的对称点是点_____.
9.如图,请你画出方格纸中的图形关于点O的中心对称图形,整个图形的对称轴的条数为____条.
10.如图,点A、A′关于点O对称,点B、B′关于O点对称,那么线段AB与A′B′的关系是____________________,四边形ABA′B′是 ______________形.
11.如图是3×4正方形网格,其中已有5各小方格涂上阴影,若再选取标有①,②,③,④中的一个小方格涂上阴影,使图中所有涂上阴影的小方格组成一个中心对称图形,则该小方格是_____.(填序号)
12.点 、 、 在数轴上对应的数分别为 、 、 ,点 在数轴上对应的数是 ,点 关于点 的对称点为 ,点 关于点 的对称点为 ,点 关于点 的对称点为 ,点 关于点 的对称点为 ,,则 的长度为________________.
三、解答题
13.两个图形成中心对称和中心对称图形有什么区别?
14.如图,已知四边形ABCD,画四边形A1B1C1D1,使它与四边形ABCD关于C点中心对称.
15.如图是由四个小正方形拼接成的L形图案,按下列 要求画出图形。
(1)请你用两种方法分别在L形图案中添画一个小正方形,使它成为轴对称图形;
(2)请你在L形图案中添画一个小正方形,使它成为中心对称图形。
(3)请你在L}形图案中移动一个小正方形,使它成为既是中心对称图形,又是轴对称图形。
16.用六根一样长的小棒搭成如图所示的图形.
(1)试移动AC,BC这两根小棒,使六根小棒成为中心对称图形;
(2)若移动AC,DE这两根,能不能也达到要求呢?(画出图形)
17.如图①,已知△ABC与△ADE关于点A成中心对称,∠B=50°,△ABC的面积为24,BC边上的高为5,若将△ADE向下折叠,如图②点D落在BC的G点处,点E落在CB的延长线的H点处,且BH=4,则∠BAG是多少度,△ABG的面积是多少.
18.如图所示,△DEF是由△ABC绕点O顺时针旋转180°后形成的图形;
(1)请你指出图中所有相等的线段;
(2)图中哪些三角形可以被看成是关于点O成中心对称关系?
19.如图所示,AD是△ABC的边BC的中线.
(1)画出以点D为对称中心,与△ABD成中心对称的三角形;
(2)若AB=10,AC=12,求AD长的取值范围.
20.已知如图所示,△AOB与△COD关于点O成中心对称,连接BC,AD.
(1)求证:四边形ABCD为平行四边形;
(2)若△AOB的面积为15 cm2,求四边形ABCD的面积.
参考答案
1.A
【解析】根据中心对称的定义可知只有A选项符合,故选A.
2.C
【解析】因为只有对称点到对称中心的距离相等,所以C选项是错误的
故选C.
3.D
【解析】根据中心对称图形的概念,可知第①④是中心对称图形.
故选:D.
4.B
【解析】试题解析:①平行四边形,是中心对称图形,而不是轴对称图形;
②矩形,是中心对称图形,也是轴对称图形;
③菱形,是中心对称图形,也是轴对称图形;
④正方形,是中心对称图形,也是轴对称图形.
综上所述,是中心对称图形,而不是轴对称图形的只有平行四边形1个.
故选B.
点睛:根据中心对称图形和轴对称图形的概念对各图形分析判断即可得解.
5.点O
【解析】对应点的连线经过对称中心.
故答案:点O.
【方法点睛】本题目是一道考查成中心对称图形的性质,每对对应点的连线都经过对称中心,且被对称中心平分.
6.相等
【解析】关于中心对称的两个图形对应线段长度是相等的.
故答案:相等.
7.对称中心
【解析】关于中心对称的两个图形,对称点的连线经过对称中心.
故答案:对称中心.
8. C D
【解析】根据中心对称图形的对称中心的定义,点C是线段AB的中点,点B是线段CD的中点,线段AB的对称中心是点C;点C关于点B成中心对称的对称点是点D.
故答案为:C;D.
9.4
【解析】如图所示,图形中的虚线是对称轴,所以对称轴有4条.
故答案为4.
10. 平行且相等 平行四边形
【解析】∵点A、A′关于点O对称,点B、B′关于O点对称,
∴OA=OA′,OB=OB′,
∴四边形ABA′B′是平行四边形,
∴AB=A′B′,AB∥A′B′.
故答案为:平行且相等;平行四边.
11.④
【解析】解:若标有①的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成的图形不是中心对称图形;
若标有②的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个轴对称图形;
若标有③的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个轴对称图形;
若标有④的一个小方格涂上阴影,则图中所有涂上阴影的小方格组成一个中心对称图形;
故答案是:④.
12.
【解析】先根据轴对称的性质找出对应边表示的数字,然后找出其中的规律,根据规律确定出表示的数,从而求得问题的答案.
解:点P关于点A的对称点P1表示的数数4;点P1关于点B的对称点P2表示的数数2;
点P2关于点C的对称点P3表示的数数8;点P3关于点A的对称点P4表示的数数-6;
点P4关于点B的对称点P5表示的数数12;点P5关于点C的对称点P6表示的数数-2;
点P6关于点A的对称点P7表示的数数4;....
2016÷6=336.所以P2016表示数为-2,所以P1 P2016=6.
【点睛】抓住对称性,寻找Pn数字规律,再根据周期算出P2016表示的数.
13.见解析
【解析】【试题分析】注意区分好成中心对称和中心对称图形的定义.
【试题解析】
前者是指具有某种特性(绕一点旋转180度后能与原图重合)的一个图形;后者是指两个图形之间,若其中某一个图形绕一点旋转180度后能与另一个图形重合,则称这两个图形之间成中心对称.
【方法点睛】本题目是一道考查成中心对称和中心对称图形的区别,重点是从定义上加以剖析.
14.见解析
【解析】试题分析:分别画出A、B、C、D各点关于点C的对称点,然后顺次连接即可.
解:四边形A1B1C1D1如图所示.
15.(1)见解析; (2)见解析; (3)见解析;
【解析】试题分析:
(1)根据原图结构,可按下列方法添加一个小正方形可使整个图形成为轴对称图形,①在下面左侧添一个小正方形;②在下面右侧添一个小正方形;③在上面右侧添一个小正方形;
(2)根据原图结构,在上面左侧添一个小正方形可使整个图形成为中心对称图形;
(3)根据原图结构,可按下列方法移动一个小正方形,可使整个图形成为中心对称图形,①将下面右侧的小正方形移到第一列的下面;②将第一列最上面的小正方形移到第二列的上面.
试题解析:
(1)按下图在的方式添加一个小正方形,整个图形是轴对称图形:
(2)按下图中的方式添加一个小正方形后整个图形是中心对称图形:
(3)按下图中的方式移动一个小正方形后整个图形是中心对称图形:
16.(1)图形见解析;
(2) 图形见解析.
【解析】试题分析:根据中心对称图形的概念求解.本题△ABC沿AB翻折可使六根小棒成为中心对称图形;移动AC、DE这两根,使它们与BC、BE沿AD翻折的图形分别重合即可.
试题解析:解:(1)如图:
(2)能,如图:
.
点睛:掌握中心对称图形的概念,判断中心对称图形的关键是要寻找对称中心,旋转180度后两部分重合.
17.∠BAG=80°,面积是14
【解析】试题分析:根据中心对称的性质和折叠的性质计算即可,同时运用了三角形的面积公式.
试题解析:依题意有AD=AB=AG,AE=AH=AC.
又∠B=50°,则∠BAG=180°-50°×2=80°;
作AD⊥BC于D,根据三角形的面积公式得到BC=9.6.
根据等腰三角形的三线合一,
可以证明CG=BH=4,则BG=5.6.
根据三角形的面积公式得△ABG的面积是14.
18.(1) AB=DE,AC=DF,BC=EF,AO=DO,BO=EO,CO=FO;(2)△ABC与△DEF,△ABO与△DEO,△ACO与△DFO,△BCO与△EFO.
【解析】【试题分析】
(1)根据中心对称图形的性质得,对应线段线段——AB=DE,AC=DF,BC=EF,对应点到旋转中心的距离相等——AO=DO,BO=EO,CO=FO;
(2)根据成中心对称图形的定义,得:△ABC与△DEF,△ABO与△DEO,△ACO与△DFO,△BCO与△EFO.
【试题解析】
(1)图中相等的线段有:AB=DE,AC=DF,BC=EF,AO=DO,BO=EO,CO=FO;
(2)图中关于点O成中心对称的三角形有:△ABC与△DEF,△ABO与△DEO,△ACO与△DFO,△BCO与△EFO.
【方法点睛】本题目是一道关于中心对称图形的性质的问题,成中心对称的两个图形,他们的对应点到旋转中心的距离相等,每对对应边相等.
19.(1)图形见解析.
(2)1
(2) 因为△ECD与△ABD成中心对称.所以AB=CE=10,所以在△ACE中,12-10
【解析】试题分析:根据成中心对称图形的性质知OA=OC,OB=OD.根据平行四边形对角线互相平分,所以可以得到四边形ABCD为平行四边形;△AOB的面积为15 cm2,则△ABC面积等于△AOB面积的2倍,因为点O为平行四边形的中心,所以△ABC的高等于△AOB高的2倍,所以S△ABC =30,所以四边形ABCD的面积是60.
(1)∵AOB与△COD关于点O成中心对称,∴OA=OC,OB=OD.
∴四边形ABCD为平行四边形.
(2)四边形ABCD的面积为60 cm2.
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 (共 2 页)
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)
同课章节目录
- 第1章 直角三角形
- 1.1 直角三角形的性质与判定(Ⅰ)
- 1.2 直角三角形的性质与判定(Ⅱ)
- 1.3 直角三角形全等的判定
- 1.4 角平分线的性质
- 第2章 四边形
- 2.1 多边形
- 2.2 平行四边形
- 2.3 中心对称和中心对称图形
- 2.4 三角形的中位线
- 2.5 矩形
- 2.6 菱形
- 2.7 正方形
- 第3章 图形与坐标
- 3.1 平面直角坐标系
- 3.2 简单图形的坐标表示
- 3.3 轴对称和平移的坐标表示
- 第4章 一次函数
- 4.1 函数和它的表示法
- 4.2 一次函数
- 4.3 一次函数的图象
- 4.4 用待定系数法确定一次函数表达式
- 4.5 一次函数的应用
- 第5章 数据的频数分布
- 5.1 频数与频率
- 5.2 频数直方图
