2.5.2 矩形的判定同步练习

21世纪教育网 –中小学教育资源及组卷应用平台
2.5.2 矩形的判定同步练习
　班级__________姓名____________总分___________
本节应掌握和应用的知识点
1. 有一个角是直角的平行四边形是矩形．
2．三个角是直角的四边形是矩形．
3．对角线相等的平行四边形是矩形．
基础知识和能力拓展精练
一、选择题
1．若O是四边形ABCD对角线的交点且OA=OB=OC=OD，则四边形ABCD是（　　）
A. 平行四边形 B. 矩形 C. 正方形 D. 菱形
2．下列判断正确的是（　　）
A. 有一个角是直角的四边形是矩形
B. 两条对角线互相平分的四边形是矩形
C. 有三个角是直角的四边形是矩形
D. 两条对角线互相垂直的四边形是矩形
3．如图，四边形ABCD的对角线AC、BD相交于点O，且AC=BD，则下列条件能判定四边形ABCD为矩形的是（ ）
A. AB=CD B. OA=OC，OB=OD C. AC⊥BD D. AB∥CD，AD=BC
4．下列检查一个门框是否为矩形的方法中，正确的是（ ）
A. 测量两条对角线，是否相等
B. 测量两条对角线，是否互相平分
C. 用曲尺测量门框的三个角，是否都是直角
D. 用曲尺测量对角线，是否互相垂直
5．平行四边形四个内角平分线相交所构成的四边形一定是（ ）
A. 一般的平行四边形 B. 一般四边形 C. 对角线互相垂直的四边形 D. 矩形
6．若顺次连接一个四边形的四边中点所组成的四边形是矩形，则原四边形一定是（ ）
A. 一般平行四边形 B. 对角线互相垂直的四边形 C. 对角线相等的四边形 D. 矩形
7．如图，已知四边形ABCD的对角线AC⊥BD，则顺次连接四边形ABCD各边中点所得的四边形是（　　）
A. 矩形 B. 菱形 C. 正方形 D. 平行四边形
8．如已知：线段AB，BC，∠ABC = 90°. 求作：矩形ABCD. 以下是甲、乙两同学的作业：
对于两人的作业，下列说法正确的是（ ）
A. 两人都对 B. 两人都不对 C. 甲对，乙不对 D. 甲不对，乙对
9．矩形ABCD中，E，F，M为AB，BC，CD边上的点，且AB=6，BC=7，AE=3，DM=2，EF⊥FM，则EM的长为（ ）
A. 5 B. C. 6 D.
二、填空题
10．如图，在四边形ABCD中，AC，BD相交于点O，AO＝OC，BO＝OD，∠ABC＝90°，则四边形ABCD是________；若AC＝5 cm，则BD＝________．
11．如图， ABCD的对角线相交于点O，请你添加一个条件____________(只添加一个即可)，使 ABCD是矩形．
12．如图，在△ABC，AB=AC，点D为BC的中点，AE是∠BAC外角的平分线，DE//AB交AE于E，则四边形ADCE的形状是___________.
13．已知：线段， ， . 求作：矩形.
以下是甲、乙两同学的作业：
甲：① 以点为圆心， 长为半径作弧；
② 以点为圆心， 长为半径作弧；
③ 两弧在上方交于点，连接， .
四边形即为所求矩形.（如图）
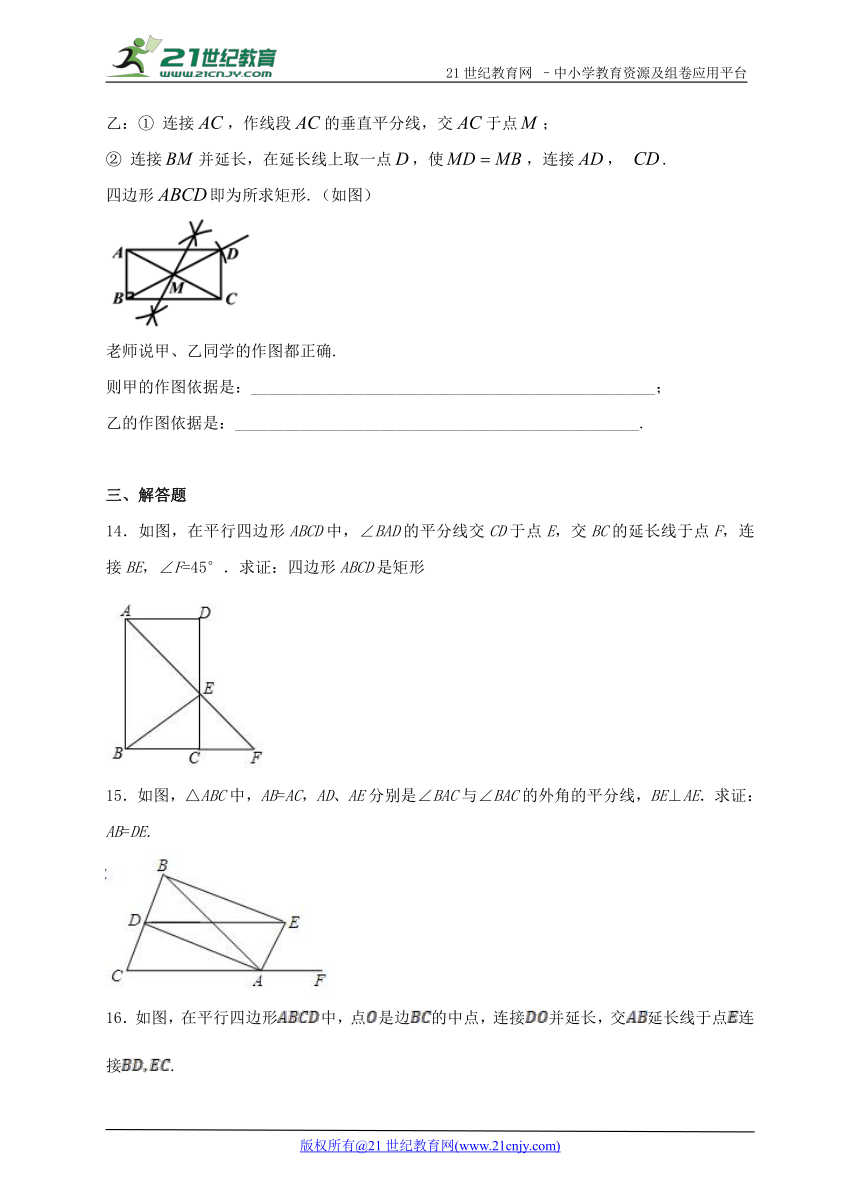
乙：① 连接，作线段的垂直平分线，交于点；
② 连接并延长，在延长线上取一点，使，连接， .
四边形即为所求矩形.（如图）
老师说甲、乙同学的作图都正确.
则甲的作图依据是：__________________________________________________；
乙的作图依据是：__________________________________________________.
三、解答题
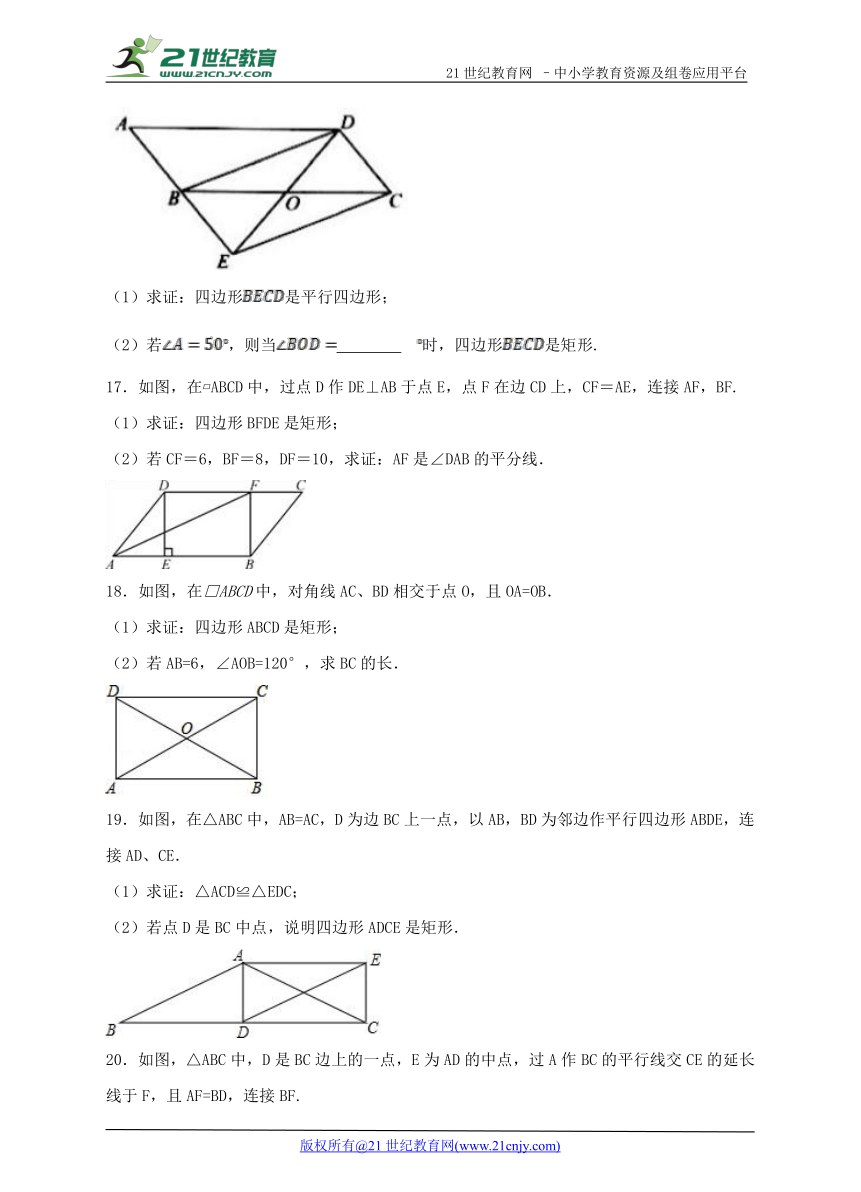
14．如图，在平行四边形ABCD中，∠BAD的平分线交CD于点E，交BC的延长线于点F，连接BE，∠F=45°．求证：四边形ABCD是矩形
15．如图，△ABC中，AB=AC，AD、AE分别是∠BAC与∠BAC的外角的平分线，BE⊥AE．求证：AB=DE.
16．如图，在平行四边形中，点是边的中点，连接并延长，交延长线于点连接.
（1）求证：四边形是平行四边形；
（2）若，则当 时，四边形是矩形.
17．如图，在 ABCD中，过点D作DE⊥AB于点E，点F在边CD上，CF＝AE，连接AF，BF.
（1）求证：四边形BFDE是矩形；
（2）若CF＝6，BF＝8，DF＝10，求证：AF是∠DAB的平分线．
18．如图，在□ABCD中，对角线AC、BD相交于点O，且OA=OB．
（1）求证：四边形ABCD是矩形；
（2）若AB=6，∠AOB=120°，求BC的长．
19．如图，在△ABC中，AB=AC，D为边BC上一点，以AB，BD为邻边作平行四边形ABDE，连接AD、CE．
（1）求证：△ACD≌△EDC；
（2）若点D是BC中点，说明四边形ADCE是矩形．
20．如图，△ABC中，D是BC边上的一点，E为AD的中点，过A作BC的平行线交CE的延长线于F，且AF=BD，连接BF.
(1)求证:BD=CD;
(2)如果AB=AC，试判断四边形AFBD的形状，并证明你的结论.
21．如图，△ABC中，点O是边AC上一个动点，过O作直线MN∥BC．设MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F．
（1）求证：OE=OF；
（2）若CE=8，CF=6，求OC的长；
（3）当点O在边AC上运动到什么位置时，四边形AECF是矩形？
并说明理由．
参考答案
1．B
【解析】试题解析：∵OA=OB=OC=OD，
∴四边形ABCD是平行四边形，AC=BD，
∴平行四边形ABCD是矩形.
故选B.
2．C
【解析】试题解析：A.有一个角是直角的平行四边形是矩形，原说法错误；
B.两条对角线互相平分的四边形是平行四边形，原说法错误；
C.有三个角是直角的四边形是矩形，原说法正确；
D.两条对角线互相垂直的四边形也可能是菱形或等腰梯形，原说法错误.
故选C.
3．B
【解析】解：A．由AB=DC，AC=BD无法判断四边形ABCD是矩形．故错误；
B．∵OA=OC，OB=OD，∴四边形ABCD是平行四边形，∵AC=BD，∴四边形ABCD是矩形．故正确；
C．由AC⊥BD，AC=BD无法判断四边形ABCD是矩形，故错误．
D．由AB∥CD，AC=BD无法判断四边形ABCD是矩形，故错误．
故选B．
点睛：本题考查矩形的判定方法、熟练掌握矩形的判定方法是解决问题的关键，记住对角线相等的平行四边形是矩形，有一个角是90度的平行四边形是矩形，有三个角是90度的四边形是矩形，属于中考常考题型．
4．C
【解析】A.两条对角线相等的四边形可能是等腰梯形，故选项A错误；
B.两条对角线互相平分的四边形可能是平行四边形，故选项B错误；
C.利用三个角是直角的四边形是矩形.故选项C正确；
D.两条对角线互相垂直的四边形可能是菱形，故选项D错误.
故选：C.
5．D
【解析】如图，四边形ABCD是平行四边形，四边形EFGH是它的四个内角平分线所围成的四边形.
∵在平行四边形ABCD中，AB∥CD，
∴∠ADC+∠DAB=180°，
∵AG、DE分别平分∠DAB、∠ADC，
∴∠ADH= EMBED Equation.DSMT4 ∠ADC，∠DAH=∠DAB，
∴∠ADH+∠DAH=（∠ADC+∠DAB）=90°，
∴∠DHA=180°-90°=90°，
∴∠GHE=90°.
同理可得：∠G=∠E=∠GFE=90°，
∴四边形EFGH为矩形.
故选D.
6．C
【解析】因为任意四边形的中点四边形都是平行四边形，而中点四边形的两组对边分别是和原四边形的两条对角线平行的，矩形相邻两边是互相垂直的，所以原四边形的对角线应该互相垂直.
故选C.
7．A
【解析】如图所示：AC⊥BD，点E、F、G、H分别是边AB、BC、CD、DA的中点；
∵在△DAC中，根据三角形中位线定理知，HG∥AC且HG= AC，
同理，在△ABC中，EF∥AC且EF= AC，
∴HG∥EF∥AC，且HG=EF，
∴四边形EFGH是平行四边形；
同理，HE∥DB；
又∵AC⊥BD，
∴HE⊥HG，
∴ EFGH是矩形；
故选A．
8．A
【解析】由甲同学的作业可知，CD=AB，AD=BC，
∴四边形ABCD是平行四边形，
又∵∠ABC=90°，
∴ ABCD是矩形．
所以甲的作业正确；
由乙同学的作业可知，CM=AM，MD=MB，
∴四边形ABCD是平行四边形，
又∵∠ABC=90°，
∴ ABCD是矩形．
所以乙的作业正确；
故选A．
9．B
【解析】
过E作EG⊥CD于G，
∵四边形ABCD是矩形，
∴∠A=∠D=90°，
又∵EG⊥CD，
∴∠EGD=90°，
∴四边形AEGD是矩形，
∴AE=DG，EG=AD，
∴EG=AD=BC=7，MG=DG DM=3 2=1，
∵EF⊥FM，
∴△EFM为直角三角形，
∴在Rt△EGM中,
EM====.
故选B.
点睛：本题考查了矩形的判定、勾股定理等知识，过E作EG⊥CD于G，利用矩形的判定可得，四边形AEGD是矩形，则AE=DG，EG=AD，于是可求MG=DG-DM=1，在Rt△EMG中，利用勾股定理可求EM．
10． 矩形 5cm
【解析】试题解析：∵AO＝OC，BO＝OD，
∴四边形ABCD是平行四边形.
∵∠ABC＝90°，
∴四边形ABCD是矩形。
∴AC=BD
∵AC=5cm
∴BD=5cm
11．OA＝OB(答案不唯一)
【解析】解：添加的条件是OA＝OB．理由是：∵ABCD是平行四边形，∴OA=OC，OB=OD．∵OA＝OB ，∴AC=BD，∴平行四边形ABCD是矩形．故答案为：OA＝OB（答案不唯一）．
点睛：本题考查了矩形的判定定理的应用，注意：对角线相等的平行四边形是矩形，此题是一道开放型的题目，答案不唯一．
12．矩形
【解析】∵AB=AC，
∴∠B=∠ACB，
∵AE是∠BAC的外角平分线，
∴∠FAE=∠EAC，
∵∠B+∠ACB=∠FAE+∠EAC，
∴∠B=∠ACB=∠FAE=∠EAC，
∴AE∥CD，
又∵DE∥AB，
∴四边形EABD是平行四边形，
∴AE平行且等于BD，
又∵BD=DC，
∴AE平行且等于DC，
故四边形ADCE是平行四边形，
又∵∠ADC=90°，
∴平行四边形EADC是矩形．
即四边形EADC是矩形．
故答案是：矩形。
【点睛】首先利用外角性质得出∠B=∠ACB=∠FAE=∠EAC，进而得到AE∥CD，即可求出四边形AEDB是平行四边形，再利用平行四边形的性质求出四边形ADCE是平行四边形，即可求出四边形ADCE是矩形．
13． 两组对边分别相等的四边形是平行四边形；有一个角是直角的平行四边形是矩形 对角线互相平分的四边形是平行四边形；有一个角是直角的平行四边形是矩形．
【解析】由甲的作图方法可知AB=CD，BC=AD，根据两组对边分别相等的四边形是平行四边形即可判定四边形ABCD为平行四边形，又因∠ABC=90°，根据有一个角是直角的平行四边形是矩形 即可判定平行四边形ABCD为矩形；由乙的作图方法可知AM=BM，BM=DM，根据对角线互相平分的四边形是平行四边形即可判定四边形ABCD为平行四边形，又因∠ABC=90°，根据有一个角是直角的平行四边形是矩形 即可判定平行四边形ABCD为矩形.
14．证明见解析.
【解析】试题分析：欲证明四边形ABCD是矩形，只需推知∠DAB是直角．
试题解析：证明：∵四边形ABCD是平行四边形，∴AD∥BC，∴∠DAF=∠F．
∵∠F=45°，∴∠DAE=45°．
∵AF是∠BAD的平分线，∴∠EAB=∠DAE=45°，∴∠DAB=90°．
又∵四边形ABCD是平行四边形，∴四边形ABCD是矩形．
15．证明见解析.
【解析】试题分析：先由角平分线和等腰三角形的性质证明AE∥BD，再由AD、AE分别是∠BAC与∠BAC的外角的平分线可证得DA⊥AE，可得AD∥BE，可证得四边形ADBE为矩形，可得结论．
试题解析：证明：∵AD、AE分别是∠BAC与∠BAC的外角的平分线，∴∠BAD+∠EAB=（∠BAC+∠FAB）=90°，∵BE⊥AE，∴DA∥BE，∵AB=AC，∴∠ABC=∠ACB，∵∠FAB=∠ABC+∠ACB=2∠ABC，且∠FAB=2∠EAB，∴∠ABC=∠EAB，∴AE∥BD，∴四边形AEBD为平行四边形，且∠BEA=90°，∴四边形AEBD为矩形，∴AB=DE．
点睛：本题主要考查矩形的判定和性质，由角平分线及等腰三角形的性质证明AE∥BD是解题的关键．
16．（1）证明见解析；（2）100°
【解析】试题分析：（1）由AAS证明△BOE≌△COD，得出OE=OD，即可得出结论；
（2）由平行四边形的性质得出∠BCD=∠A=50°，由三角形的外角性质求出∠ODC=∠BCD，得出OC=OD，证出DE=BC，即可得出结论．
试题解析:（1）∵四边形ABCD为平行四边形，
∴AB∥DC，AB=CD，
∴∠OEB=∠ODC，
又∵O为BC的中点，
∴BO=CO，
在△BOE和△COD中，
，
∴△BOE≌△COD（AAS）；
∴OE=OD，
∴四边形BECD是平行四边形；
（2）若∠A=50°，则当∠BOD=100°时，四边形BECD是矩形．理由如下：
∵四边形ABCD是平行四边形，
∴∠BCD=∠A=50°，
∵∠BOD=∠BCD+∠ODC，
∴∠ODC=100°-50°=50°=∠BCD，
∴OC=OD，
∵BO=CO，OD=OE，
∴DE=BC，
∵四边形BECD是平行四边形，
∴四边形BECD是矩形；
17．（1）证明见解析；（2）见解析
【解析】试题分析：（1）根据已知条件易证四边形BFDE是平行四边形，再证明∠DEB=90°即可得结论；（2）根据已知条件证明AD＝DF，根据等腰三角形的性质可得∠DAF＝∠DFA；再由AB∥CD，可得∠DFA＝∠FAB.即可得∠DAF＝∠FAB，结论得证.
试题解析：
证明：（1）∵四边形ABCD是平行四边形，
∴AB∥CD，AB＝CD.
又∵CF＝AE，
∴BE＝DF.
又∵BE∥DF，
∴四边形BFDE为平行四边形．
∵DE⊥AB，
∴∠DEB＝90°.
∴四边形BFDE是矩形．
（2）∵四边形BFDE是矩形，
∴∠BFD＝90°.∴∠BFC＝90°.
在Rt△BFC中，由勾股定理，得BC＝＝＝10.
∴AD＝BC＝10.
又∵DF＝10，
∴AD＝DF.
∴∠DAF＝∠DFA.
∵AB∥CD，
∴∠DFA＝∠FAB.
∴∠DAF＝∠FAB.
∴AF是∠DAB的平分线．
18．（1）见解析；（2）2．
【解析】试题分析：（1）根据平行四边形的性质求出AO=OC，BO=OD，求出AC=BD，根据矩形的判定推出即可；
（2）根据矩形性质求出∠ABC=90°，求出∠CAB=30°，解直角三角形求出即可．
试题解析：（1）证明：∵四边形ABCD是平行四边形，
∴AO=OC，BO=OD，
∵OA=OB，
∴OA=OB=OC=OD，
∴AC=BD，
∴四边形ABCD是矩形；
（2）解：∵∠AOB=120°，OA=OB，
∴∠OAB=∠OBA=30°，
∵四边形ABCD是矩形，
∴∠ABC=90°，
∴AC=2BC，
∴AB= ，
∴BC=AB=6×=2．
19．(1)证明过程见解析；(2)证明过程见解析.
【解析】（1）根据平行四边形的性质、等腰三角形的性质，利用全等三角形的判定定理SAS可以证得△ADC≌△ECD；
（2）利用等腰三角形的“三合一”性质推知AD⊥BC，即∠ADC=90°；由平行四边形的判定定理（对边平行且相等是四边形是平行四边形）证得四边形ADCE是平行四边形，所以有一个角是直角的平行四边形是矩形．
证明：（1）∵四边形ABDE是平行四边形
∴AB∥DE，AB=DE；∴∠B=∠EDC；
又∵AB=AC，∴AC=DE，∠B=∠ACB，
∴∠EDC=∠ACD
∴△ADC≌△ECD（SAS）；
（2）∵四边形ABDE是平行四边形
∴BD∥AE，BD=AE，∴AE∥CD；
又∵BD=CD，∴AE=CD（等量代换）
∴四边形ADCE是平行四边形；
在△ABC中，
AB=AC，BD=CD，
∴AD⊥BC，
∴∠ADC=90°，
∴四边形ADCE是矩形．
20．（1）证明见解析；（2）当AB=AC时，四边形AFBD是矩形，证明见解析.
【解析】试题分析：（1）根据平行线的性质得到∠AFE=∠DCE，由中点的定义得到AE=DE，根据三角形全等的判定易证得△AFE≌△DCE，利用全等三角形的性质得AF=DC，而AF=BD，即可得到D是BC的中点；
（2）在（1）的基础上，根据全等三角形的性质和有三个角都是直角的四边形是矩形.
试题解析：证明:∵AF∥BC，∴∠AFE=∠ECD.
又∵E为AD的中点，∴AE=DE.
在△AFE与△DCE中，∵
∴△AFE≌△DCE(AAS)，∴AF=CD.
又∵AF=BD，∴BD=CD.
(2)解:当AB=AC时，四边形AFBD是矩形.
证法一:由(1)知，D为BC的中点，又∵AB=AC，
∴AD⊥BC.
∵AF∥BC，∴∠DAF=∠ADB=90°.
∵△AFE≌△DCE(已证)，∴CE=EF.
∴DE为△BCF的中位线，∴DE∥BF.
∴∠FBD=∠EDC=90°，
∴四边形AFBD是矩形.
证法二:∵AF=BD，AF∥BD，
∴四边形AFBD是平行四边形.
由(1)知，D为BC的中点，又∵AB=AC，
∴AD⊥BC(三线合一)，即∠BDA=90°.
∴ AFBD是矩形.
21．（1）证明见解析；（2）5；（3）当点O在边AC上运动到AC中点时，四边形AECF是矩形．证明见解析.
【解析】试题分析：（1）根据平行线的性质以及角平分线的性质得出∠1=∠2，∠3=∠4，进而得出答案；（2）根据已知得出∠2+∠4=∠5+∠6=90°，进而利用勾股定理求出EF的长，即可得出CO的长；（3）根据平行四边形的判定以及矩形的判定得出即可．
试题解析：（1）证明：∵MN交∠ACB的平分线于点E，交∠ACB的外角平分线于点F，
∴∠2=∠5，∠4=∠6，
∵MN∥BC，
∴∠1=∠5，∠3=∠6，
∴∠1=∠2，∠3=∠4，
∴EO=CO，FO=CO，
∴OE=OF；
（2）∵∠2=∠5，∠4=∠6，
∴∠2+∠4=∠5+∠6=90°，
∵CE=8，CF=6，
∴EF==10，
∴OC=EF=5；
（3）当点O在边AC上运动到AC中点时，四边形AECF是矩形．
证明：当O为AC的中点时，AO=CO，
∵EO=FO，
∴四边形AECF是平行四边形，
∵∠ECF=90°，
∴平行四边形AECF是矩形．
21世纪教育网 www.21cnjy.com 精品试卷·第 2 页 （共 2 页）
HYPERLINK "http://www.21cnjy.com/" 版权所有@21世纪教育网(www.21cnjy.com)